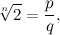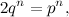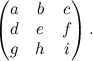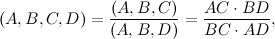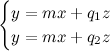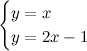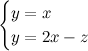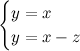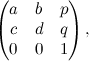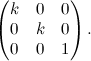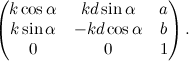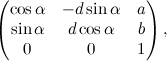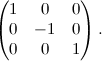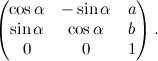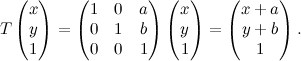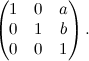Erlangen 1872 — Coniche e retta impropria

Le rette sono tutte rappresentabili da equazioni di primo grado nelle due incognite x e y; viceversa, ogni equazione in due incognite rappresenta una retta (purché l'equazione non sia una roba strana e impossibile come 1=0).

Quindi le rette sono fatte così: ax+by+c=0 (con a e b non contemporaneamente uguali a zero).

Ora passiamo alle equazioni di secondo grado. Prima di tutto: come sono fatte? Ricordando che le incognite sono due, e che quindi esiste anche il termine xy, di secondo grado, una generica equazione è fatta così:

Ax²+Bxy+Cy²+Dx+Ey+F=0.

Bene: le coniche sono tutte equazioni di secondo grado. Vale anche il viceversa se consideriamo coniche anche oggetti strani come x²+y²=-1, che è una equazione che non rappresenta niente (non esistono valori di x e di y che la soddisfano) e che ci permettiamo dunque di chiamare circonferenza immaginaria. Ci sono anche oggetti un po' meno strani, come per esempio x²-y²=0, che si trasforma in (x+y)(x-y)=0, e che geometricamente è interpretabile come l'insieme di due rette: la chiamiamo iperbole degenere — in pratica è una iperbole coincidente con i propri asintoti, è come se noi prendessimo un cono e lo tagliassimo con un piano che lo attraversa e passa anche per il suo vertice.

Ecco un'immagine che ci mostra una iperbole degenere:

E, già che ci siamo, ecco una parabola degenere (cioè due rette coincidenti):

Ed ecco una ellisse, o circonferenza, degenere (in pratica è un punto solo soletto):

Ora la domanda è: come riconosciamo se una generica equazione di secondo grado rappresenta una iperbole, una parabola o una ellisse? Qui ci viene in aiuto la retta impropria.

La sostanza è questa: una ellisse è una curva tranquilla, chiusa, la vediamo tutta, non fugge lontano: la retta impropria non sa neanche cosa sia. Una iperbole, al contrario, va all'infinito, e ci va oltretutto lungo due direzioni diverse: quindi incontra la retta impropria, e lo fa in due punti. Una parabola è una via di mezzo: va all'infinito, ma ci va lungo la stessa direzione, per così dire: tocca cioè la retta impropria in un solo punto.

Ora vediamo i calcoli.

Primo giorno di scuola

La migliore battuta su facebook dopo il primo giorno di lezione (oggi):

-1: l'estate si avvicina

Erlangen 1872 — Coniche, similitudini e affinità

Le circonferenze sono tutte simili, le parabole anche, le ellissi e le iperboli no.

Intuitivamente, diremmo che queste due ellissi hanno forma diversa, una è più schiacciata dell'altra: si dice che hanno eccentricità diversa. Non si può ingrandire la più piccola per farla diventare uguale a quella più grande: non esiste nessuna similitudine che porta una nell'altra.

Anche per una iperbole vale lo stesso discorso, anche se è più difficile da capire: in figura, oltre all'iperbole, sono rappresentati altri oggetti. Le due rette tratteggiate corrispondono al profilo del cono dal quale è stata ritagliata l'iperbole: si chiamano asintoti e sono due rette che approssimano l'iperbole, man mano che la curva si allontana dal centro. Il rettangolo è quello che ci dà la forma dell'iperbole: una similitudine permette di trasformare un'iperbole in un'altra avente un rettangolo simile a quello di partenza. Cambiando le proporzioni del rettangolo, cambiano le iperboli.

Riassumendo: se ci mettiamo nella geometria delle similitudini, esiste un'unica parabola, esistono tante ellissi diverse, ed esistono tante iperboli diverse.

Se invece passiamo alle affinità, le cose sono più semplici: tutte le ellissi sono trasformabili una nell'altra, e così pure tutte le iperboli (e naturalmente tutte le parabole, dato che bastava una similitudine). Quindi nella geometria affine esistono una sola parabola, una sola ellisse e una sola iperbole. La circonferenza fa naturalmente parte della famiglia delle ellissi.

Ora vediamo un'altra caratteristica comune a tutte le coniche.

Lezione

A volte mi piacerebbe fare lezione così.



(Via Gravità Zero)

Erlangen 1872 — Coniche

Circonferenza, parabola, ellisse, iperbole: tutte queste curve fanno parte della categoria delle coniche. Perché?

Partiamo dalla definizione: cosa sono quelle curve? Cosa hanno in comune, e quali sono le differenze?

Prima di tutto: esistono due modi per definirle. Sono luoghi di punti, e sono sezioni di cono.

Per esempio, una circonferenza è il luogo dei punti equidistanti da un punto (che viene detto centro). Guardando la figura, per ogni punto P la distanza PO rimane costante.

Una ellisse è il luogo dei punti per i quali rimane costante la somma delle due distanze da due punti (che vengono detti fuochi). Sempre facendo riferimento alla figura, la somma PF₁+PF₂ rimane costante.

Una parabola è il luogo dei punti equidistanti da un punto (detto fuoco) e da una retta (detta direttrice). In figura, PF è uguale a PH:

E infine, una iperbole è il luogo dei punti per i quali rimane costante la differenza in valore assoluto delle distanze tra due punti (detti fuochi). In figura, |PF₁ - PF₂| è costante:

Tutte queste curve sono anche definibili in un altro modo. Prendiamo quello che si definisce cono circolare retto, il che significa che dobbiamo prendere una retta, tenerla stretta per un punto e farla ruotare con una certa ampiezza. Quello che otteniamo è una cosa del genere:

Ora cominciamo a tagliare a fette questo doppio cono: a seconda dell'inclinazione del nostro coltello, possiamo ottenere figure diverse.

Se il piano secante è parallelo alla generatrice del cono (diciamo che la generatrice è il lato, ma non ditelo in una interrogazione) abbiamo la figura 1: una parabola. Se il piano forma un angolo sufficientemente grande con l'asse del cono (maggiore di quello formato dalla generatrice) siamo nel caso 2: una ellisse. La circonferenza è un caso particolare: si ottiene quando il piano è perpendicolare alla generatrice. Se il piano forma un angolo piccolo con l'asse del cono (minore di quello formato dalla generatrice) abbiamo una iperbole: questo è il caso 3. Ecco perché queste curve si chiamano coniche: perché si ottengono tutte come sezioni dello stesso cono.

Bene, ora ripensiamo alle isometrie: che succede se trasformiamo una conica con una isometria?

La risposta è: niente di speciale: una circonferenza rimarrà una circonferenza, una ellisse rimarrà una ellisse, e così vale per le parabole e le iperboli. Non solo: una circonferenza non verrà trasformata in una circonferenza di raggio diverso, una ellisse non verrà trasformata in una ellisse con assi di lunghezze diverse, una parabola manterrà costante la distanza tra fuoco e direttrice, e una iperbole manterrà costante la distanza tra i fuochi (e un'altra caratteristica che si chiama asse immaginario, sulla quale non ci fermiamo troppo: diciamo che nemmeno l'iperbole cambia forma).

La prossima volta vediamo cosa combinano le similitudini e le affinità.

Un semplice esercizio

Teorema: per ogni n maggiore di 2, è irrazionale.

Dimostrazione:

Supponiamo per assurdo che la radice n-esima di 2 sia razionale: allora può essere scritta come frazione nel modo seguente:

con p e q interi positivi. Elevando alla n ed eliminando il denominatore, si ottiene l'espressione

che può essere riscritta così:

Un teoremino dimostrato da Andrew Wiles ci fa concludere che p e q non esistono. C.V.D.

(Via: 360, ctk)

Erlangen 1872 — Proiettività

Quando abbiamo scritto per la prima volta le equazioni di una trasformazione geometrica, abbiamo detto che la matrice associata era una matrice 3×3, e non 2×2, per cui un generico punto doveva essere scritto come terna (x,y,1) e non come coppia (x,y).

Avevamo detto che c'erano due motivi per cui erano necessarie tre coordinate: uno era perché così le cose funzionano; la spiegazione del secondo motivo era stata rimandata.

Ecco, ora vediamo qual è il secondo motivo: in realtà quelle trasformazioni sono molto più comprensibili se ci mettiamo nel mondo delle coordinate omogenee. Tutte le trasformazioni viste fino ad ora operavano su punti del tipo (x,y,1), che possiamo vedere come punti propri.

Se le generalizziamo a punti di coordinate (x,y,z), senza porre condizioni su z, osserviamo che tali trasformazioni lasciano sempre fissa la retta impropria. Insomma: le affinità (che costituiscono il gruppo di trasformazioni più grande che abbiamo considerato finora) trasformano punti propri in punti propri, e punti impropri in punti impropri.

Il passo successivo è dunque questo: generalizziamo ulteriormente, e consideriamo trasformazioni che mettono in movimento anche la retta impropria. Queste nuove trasformazioni si chiamano proiettività.

La matrice associata a una generica proiettività è semplicemente questa:

Sembrerebbe quindi che le proiettività siano trasformazioni troppo generali da poter avere qualche caratteristica che le contraddistingue, o qualche invariante (l'unica richiesta che viene fatta sulla matrice è che il suo determinante non sia nullo). Non è così: un invariante esiste anche qua, ed ha lo strano nome di birapporto di quattro punti allineati.

È definito in questo modo:

dove con (A,B,C) si intende il rapporto semplice di tre punti allineati, già definito quando abbiamo parlato di affinità.

Bene, le proiettività formano gruppo, che comprende come sottogruppi tutti quelli visti finora, dalle affinità in giù. Con le proiettività ci si diverte un sacco.

Erlangen 1872 — Retta impropria

Che cosa rappresenta l'equazione x=0?

È quella retta avente tutti i punti con ascissa uguale a zero, cioè è l'asse delle y.

Come si trasforma l'equazione se la mettiamo in coordinate omogenee?

Dato che non ci sono termini noti, in coordinate omogenee l'asse delle y ha sempre equazione x=0. Facile.

Cosa possiamo dire riguardo l'equazione y=0? Analogamente a quanto detto prima, y=0 è l'equazione dell'asse delle x, scritta sia in coordinate non omogenee che in coordinate omogenee. Facile.

Se ci mettiamo in coordinate omogenee, cosa rappresenta l'equazione z=0?

Ecco la novità: z=0 è una equazione di primo grado, e dunque siamo autorizzati a chiamarla retta. Ma qual è la caratteristica comune di tutti i suoi punti? Hanno tutti la terza coordinata uguale a zero, quindi sono tutti punti impropri. La retta di equazione z=0 viene detta retta impropria, e non è disegnabile sul piano cartesiano. Molti dicono che assomiglia a una circonferenza con raggio infinito e centro nell'origine, e in un certo senso hanno ragione.

Esiste però un modo per visualizzarla: basta cambiare punto di vista.

Nella realtà le righe blu del quadro qua sopra sarebbero parallele, eppure si incontrano tutte in un punto. Bene, quello è il punto improprio comune a tutte le rette blu. Dove si trova? Sulla linea dell'orizzonte: ecco, quella è la retta impropria. Ogni punto della linea dell'orizzonte rappresenta una diversa direzione.

Queste considerazioni ci consentono di aprire le porte della geometria proiettiva.

Erlangen 1872 — Punti impropri

Insomma, sembra che le coordinate omogenee portino solo complicazioni: non solo non c'è più una corrispondenza biunivoca tra punti del piano e coordinate, ma succede anche di peggio: le rette parallele si incontrano. E, tanto per girare il coltello nella piaga, nell'esempio che abbiamo visto si incontrano in un punto la cui terza coordinata è uguale a zero: se ci ricordiamo che la terza coordinata è quel numero che va messo al denominatore, quando dobbiamo risalire dalle coordinate omogenee a quelle normali, siamo a posto.

Bé, in realtà tutti questi problemi sono voluti.

Vediamo di capire il perché con un esempio più generale di quello della volta scorsa: prendiamo due rette parallele,

(ci ricordiamo che due rette parallele hanno lo stesso coefficiente angolare m, vero?) e le trasformiamo in coordinate omogenee,

e le mettiamo a sistema:

Se risolviamo, otteniamo z=0 e y=mx: questo significa che una generica soluzione del sistema può essere scritta come (x,mx,0) o, se vogliamo, (1,m,0).

Quindi due rette parallele si incontrano in un punto la cui terza coordinata è sempre uguale a zero, mentre le prime due godono della seguente proprietà: se poniamo uguale a 1 la prima, la seconda è uguale a m. Detto in termini un po' più pratici: due rette parallele si incontrano in un punto che dipende solo dalla loro direzione.

Cominciamo dunque a fare un po' di ordine: il mondo si divide in due categorie. La prima, quella dei punti normali,  è costituita dalle terne la cui terza coordinata è diversa da zero (e che, quindi, grazie al fatto che le coordinate omogenee sono definite a meno di una costante moltiplicativa, possiamo porre uguale a 1). La seconda è costituita dai punti strani, aventi terza coordinata uguale a zero. Questi punti non sono veri punti, ma sono in corrispondenza con tutte le possibili direzioni che le rette possono avere.

La prima categoria, quella dei punti normali, viene detta dei punti propri. La seconda, invece, è quella dei punti impropri.

I punti impropri ci permettono di accedere a un mondo meraviglioso.

Altro che orologi digitali

L'arte della fabbricazione degli orologi (funzionanti).

(Via)

Erlangen 1872 — Convergenze parallele

Si tratta di fare un passo ardito. Ma, per capire bene, bisogna fare qualche calcoletto.

Prendiamo l'equazione di una retta, per esempio y=x: è una equazione molto semplice, che rappresenta la bisettrice del primo e del terzo quadrante.

Prendiamone un'altra, per esempio y=2x-1. Se le rappresentiamo sul piano, otteniamo questo grafico:

Sono due rette secanti; se vogliamo trovare le coordinate del loro punto di intersezione, dobbiamo risolvere il sistema tra le due equazioni, che è il seguente:

Con una semplice sostituzione si trova la soluzione, che è proprio x=1, y=1, come si vede anche dal grafico.

Bene: rifacciamo i calcoli in coordinate omogenee.

Come si trasformano le equazioni? Non è difficile: ogni volta che si trova una x si sostituisce x/z, e ogni volta che si trova una y si sostituisce y/z. Quindi le equazioni delle due rette diventerebbero:

E ora il passo ardito: eliminiamo i denominatori senza porci troppi problemi, e rimettiamo a sistema il tutto;

Cosa è successo? Prima di tutto l'equazione di una delle due rette è cambiata, e in secondo luogo abbiamo un sistema in tre equazioni e due incognite. Vediamo di capirci qualcosa.

Primo fatto: se l'equazione originale non aveva termine noto (si dice che era omogenea), allora trasformandola in coordinate omogenee non cambia. Infatti senza termini noti si osserva che z è un denominatore comune, che si può togliere senza scrupoli (se per caso capita da queste parti uno studente di prima superiore: normalmente questa semplificazione è considerata un errore, servono le condizioni di esistenza, eh).

Se l'equazione originale invece aveva termine noto (cioè era non omogenea), la trasformazione in coordinate omogenee la fa diventare omogenea (guarda un po'). Insomma, il termine noto acquisisce una z.

Secondo fatto: un sistema di due equazioni in tre incognite non ha un unico risultato, di solito: ci sono troppe incognite. Se proviamo a risolvere per sostituzione il sistema scritto sopra, otteniamo x=z, e non abbiamo ulteriori equazioni per determinare il valore di z. La soluzione del sistema, utilizzando queste nuove coordinate, diventa quindi (z,z,z). Dividendo tutto per z, otteniamo (1,1,1). Che, in coordinate omogenee, rappresenta il punto (1,1).

Riassunto: abbiamo effettivamente complicato le cose semplici.

Ma allora, perchè lo facciamo?

La risposta è data dal seguente esempio. Proviamo a calcolare l'intersezione tra le due rette y=x e y=x-1.

Le due rette sono parallele, quindi non hanno intersezione. Effettivamente, il sistema tra le loro due equazioni, in coordinate cartesiane, è impossibile. E quello in coordinate omogenee?

Eccolo qua:

Sostituendo x al posto di y nella seconda equazione, otteniamo z=0. Quindi questo sistema ammette soluzione! Tutte le terne del tipo (x,x,0) vanno bene. Dividendo per x, otteniamo ad esempio come soluzione il punto (1,1,0). Quindi il sistema tra le equazioni delle due rette parallele ha soluzione.

Quindi due rette parallele si incontrano in un punto. E buonanotte a Euclide.

Erlangen 1872 — Coordinate omogenee

La battaglia navale ci ha insegnato a trattare le coordinate cartesiane con una certa naturalezza. Un punto sul piano è identificato da una coppia di numeri (x,y), e viceversa una coppia di numeri identifica in modo univoco un punto sul piano.

Non contenti di questa situazione, complichiamo le cose. Ora utilizziamo una terna di numeri, (x₁,x₂,x₃), legata alle coordinate (x,y) da queste due relazioni:

Vediamo qualche esempio: l'origine degli assi, che normalmente avrebbe coordinate (0,0), con questo nuovo sistema verrebbe ad avere coordinate (0,0,1). Ma andrebbero bene anche le coordinate (0,0,2), (0,0,7), e qualunque terna del tipo (0,0,a). Il punto (3,14) potrebbe essere scritto come (3,14,1), oppure (3π,14π,π), e così via.

Insomma, un generico punto di coordinate (x,y) può essere scritto in un'infinità di modi: se a è un qualunque numero diverso da zero, allora (x,y) è uguale a (xa,ya,a). Tutte le terne che si ottengono una dall'altra moltiplicando per una opportuna costante rappresentano lo stesso punto sul piano cartesiano: per questo motivo queste nuove coordinate vengono dette coordinate omogenee. Per evitare confusione ci si può mettere d'accordo e decidere di tenere sempre uguale a 1 la terza coordinata, ma non è obbligatorio.

Bisogna anche dire che dopo un po' ci si scoccia di tutti quegli indici, quando si scrivono le incognite x₁, x₂, x₃, soprattutto se ci si mette a fare qualche calcolo (pensate ai sistemi di equazioni). Quindi, commettendo quello che i Veri Matematici chiamano abuso di linguaggio, si tende a non usare la scrittura (x₁,x₂,x₃), ma si preferisce utilizzare (x,y,z) — ricordandosi naturalmente che la x di (x,y) è uguale a x/z di (x,y,z).

Riassunto: avevamo delle belle coordinate cartesiane, in cui c'era una corrispondenza biunivoca tra i punti del piano e le coppie del tipo (x,y), e ora abbiamo delle coordinate omogenee, in cui non c'è più una corrispondenza biunivoca coi punti del piano, in cui le terne del tipo (xa,ya,za) rappresentano tutte lo stesso punto, purché za sia diverso da zero. Abbiamo complicato abbastanza?

No, non abbiamo ancora parlato di quello che succede quando z=0.

Erlangen 1872 — Omologie e affinità

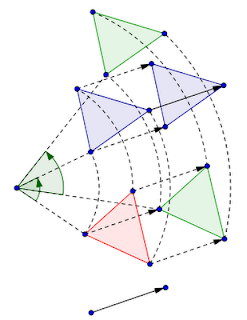
L'omologia è una trasformazione un po' complicata da spiegare. Vediamo prima un disegno:

Per definire una omologia servono tre elementi: una retta (quella orizzontale nel disegno), una direzione (il vettore) e un numero k (nel disegno ho preso k=2). Poi si procede nel modo seguente: si proietta un qualsiasi punto della figura (il triangolo rosso) sulla retta data, e si moltiplica per k il segmento che va dal punto proiettato sulla retta al punto corrispondente sulla figura. Insomma, il segmento retta-figura blu è il doppio del segmento retta-figura rossa.

Bene, questa roba certamente non è una similitudine: infatti dobbiamo rinunciare a un po' di invarianti. L'ortogonalità non si mantiene più, ma il parallelismo sì. Quindi si può affermare che i parallelogrammi si trasformano in parallelogrammi, ma i rettangoli non rimangono rettangoli.

L'invariante che viene utilizzato in questo tipo di geometria ha un nome strano: si chiama rapporto semplice di tre punti allineati. Dati cioè tre punti A, B e C sulla stessa retta, il rapporto semplice si indica con (A,B,C) ed è uguale a AC/BC (la formula contempla anche i casi di punti coincidenti, e se BC è uguale a zero allora si assegna al rapporto semplice il valore di infinito).

Per poter costruire una nuova geometria dobbiamo combinare queste nuove trasformazioni con le vecchie: se componiamo le omologie con le similitudini, otteniamo il gruppo delle affinità.

Esistono poi alcuni risultati che ci fanno capire qualcosa di più: una qualsiasi affinità si può ottenere componendo una similitudine e al più due omologie. E poi: una qualsiasi affinità si può ottenere componendo una isometria e al più due omologie ortogonali (aventi cioè il vettore ortogonale all'asse) con gli assi ortogonali tra loro. Oppure ancora: una qualsiasi affinità si può ottenere componendo una traslazione più un'altra affinità avente almeno un punto fisso.

Ecco un disegno che rappresenta una omologia ortogonale e che mostra la trasformazione di una circonferenza in una ellisse.

E dunque, dal punto di vista della geometria affine, non c'è differenza tra circonferenza ed ellisse. In questa geometria ci sono solo tre curve di secondo grado diverse: l'ellisse, la parabola e l'iperbole (non tre tipi di curve, ma proprio tre curve in tutto).

La matrice associata a una generica affinità è questa:

dove a, b, c, d, p, q sono numeri qualsiasi (purché la matrice 2×2 che contiene a, b, c, d non abbia determinante nullo). E quindi non c'è spazio per ulteriori generalizzazioni, a meno che non cominciamo a pensare di dare un significato a quella misteriosa terza riga.

Ora viene il bello.

Erlangen 1872 — Omotetie e similitudini

Prendiamo un foglio, con tante belle formule scritte sopra, e fotocopiamolo in modo da ridurlo alle dimensioni di un francobollo. Questa è una trasformazione che certamente non conserva le distanze, e quindi non è una isometria.

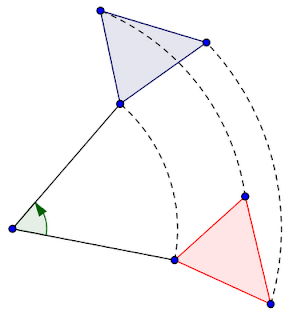
La trasformazione base che permette di costruire ingrandimenti o rimpicciolimenti si chiama omotetia, ed è definita una volta fissati un punto (detto centro) e un numero k, che rappresenta il fattore di ingrandimento o rimpicciolimento. Ecco una figurina:

Si costruiscono i segmenti che vanno dal centro C ai vertici della figura (quella rossa), poi questi segmenti devono essere moltiplicati per k (in questa figura k è uguale a 2: i segmenti sono raddoppiati).

La matrice associata a una omotetia avente centro nell'origine e rapporto k è:

Le omotetie di centro C formano un gruppo: l'elemento neutro è l'omotetia che si ottiene per k=1, e l'inverso dell'omotetia di rapporto k è quella di rapporto 1/k. Questo gruppo è però un po' troppo piccolo per poterci fare della geometria, e quindi lo allarghiamo aggiungendovi tutte le isometrie: questo ci consente di spostare le figure in giro per il piano un po' come vogliamo, mentre la solo omotetia ci obbligherebbe a tenere le figure in posizioni ben precise, in modo da avere i vertici allineati col centro.

Il gruppo delle isometrie più le omotetie si chiama gruppo delle similitudini, di cui abbiamo probabilmente sentito parlare, forse alle scuole medie, forse alle superiori. Non ho trovato consenso in giro per la rete per quanto riguarda il nome di questa geometria: qualcuno non associa un nome particolare, qualcun altro la chiama geometria elementare. Chiamiamola così fino a che qualche autorità non interviene a correggere.

Una similitudine non ha, naturalmente, tutti gli invarianti di una isometria. La similitudine non conserva le lunghezze, ad esempio. Nella similitudine si conservano, invece, i rapporti tra le distanze. Quindi le circonferenze vengono trasformate in circonferenze, i segmenti in segmenti, le rette in rette, vengono conservati il parallelismo, la perpendicolarità e le ampiezze degli angoli. Il gruppo delle isometrie è un sottogruppo di quello delle similitudini: questo significa che ogni isometria è anche una similitudine, ma non è vero il viceversa.

E ora cerchiamo di capire il senso di questa suddivisione in tante geometrie. Prendiamo queste due circonferenze:

Non sono uguali, nel senso che non sono composte dagli stessi punti. Non sono uguali nemmeno nel senso della geometria euclidea: non sono cioè congruenti; non esiste nessuna isometria che trasforma una nell'altra. Esse sono invece uguali nel senso della geometria elementare, cioè sono simili.

Quindi in questo tipo di geometria esiste un solo tipo di circonferenza, mentre esistono vari tipi di ellissi, così come esistono vari tipi di rettangoli (ricordiamo la differenza tra un televisore in formato 4:3 e uno in 16:9). Forse non tutti sanno che esiste un solo tipo di parabola: le parabole sono tutte simili tra loro.

La matrice associata a una generica similitudine è questa (dove d è sempre uguale a +1 oppure -1 a seconda del tipo di trasformazione, diretta oppure inversa):

Questo è tutto: per allargare ancora un po' il gruppo, bisogna considerare qualche nuova trasformazione.

Erlangen 1872 — Isometrie

Abbiamo finalmente un gruppo abbastanza grosso da poterci lavorare sopra: quello delle isometrie. La cui matrice associata, nel caso più generale possibile, è la seguente:

dove d vale +1 oppure -1 a seconda del tipo di isometria: +1 per quelle dirette e -1 per quelle inverse.

Una prima considerazione: cosa si intende quando si afferma che due figure sono uguali? Per esempio, due circonferenze con lo stesso raggio sono uguali? Si sarebbe portati a rispondere di sì, ma non è proprio corretto: se le due circonferenze hanno due centri diversi, esse non sono composte dagli stessi punti. Quindi non sono davvero uguali. Se prendo un foglio a quadretti e disegno, in cima alla pagina, un segmento lungo tre quadretti e, in fondo alla pagina, un altro segmento lungo tre quadretti, posso dire che sono uguali? Anche se sono composti da punti che sono tutti diversi?

In un certo senso, le due circonferenze o i due segmenti sono davvero uguali, ma si tratta di capire bene quale sia, questo certo senso. È questa l'idea che sta alla base del programma elaborato Klein.

Abbiamo costruito un gruppo di trasformazioni geometriche, le isometrie. Queste muovono, in tanti modi diversi, i punti del piano: a noi interessa capire se queste trasformazioni hanno qualcosa in comune. Detto in altri termini: a noi interessa capire quali sono gli invarianti di queste trasformazioni. E la parola isometria non è stata scelta a caso: essa ci dice quali caratteristiche vengono mantenute dalle traslazioni, dalle rotazioni, dalle simmetrie e da tutte le loro composizioni.

Le isometrie mantengono le distanze tra i punti.

Se con T indichiamo una generica isometria, la lunghezza del segmento AB è uguale a quella del segmento T(AB).

Due figure che si corrispondono in una isometria si dicono congruenti, o isometriche (o, se vogliamo, anche uguali, ma non nel senso di composte dagli stessi punti; è per questo che si tende a non usare la parola uguali in geometria). Lo studio della congruenza tra figure piane è quello che fa diventare matti gli studenti di prima superiore: la geometria che si ottiene è detta geometria euclidea (anche se negli Elementi di Euclide non compare solo questo tipo di geometria).

Si dimostra che le isometrie trasformano circonferenze in circonferenze, segmenti in segmenti, rette in rette, mantengono il parallelismo, la perpendicolarità e le ampiezze degli angoli. Insomma, godono di tutte quelle proprietà che tanto amiamo.

Ora vediamo di fare a meno di qualcuna di queste proprietà.

Erlangen 1872 — Simmetrie

Eccoci a una nuova trasformazione: la simmetria assiale.

Qui abbiamo una novità, rispetto alle traslazioni e alle rotazioni: l'orientazione della figura viene invertita. Se percorriamo in senso antiorario i vertici della figura rossa, vediamo che i vertici della figura blu vengono percorsi in senso orario, e viceversa. È come se la figura venisse staccata dal foglio, capovolta e poi riappoggiata: con le traslazioni e con le rotazioni questo non succedeva.

Le simmetrie assiali non formano un gruppo: se ne componiamo due, quello che risulta non è più una simmetria assiale (infatti se si varia l'orientazione due volte, è come se non si fosse fatto nulla: la composizione di due simmetrie assiali è una isometria diretta).

Per potere avere un gruppo bisogna allargare un po' l'insieme: assieme alle simmetrie bisogna comprendere anche le isometrie dirette. Il gruppo che si ottiene è detto delle isometrie (senza specificare se sono dirette o inverse). Proviamo a descriverlo: esso contiene, come abbiamo già visto, tutte le traslazioni, le rotazioni, e le simmetrie assiali. Contiene altro? Certamente contiene le rototraslazioni, di cui abbiamo già parlato. Le simmetrie centrali contano poco: sono in realtà rotazioni di un angolo piatto intorno a un punto. C'è altro?

Sì, come combinando una rotazione e una traslazione otteniamo una trasformazione più generale, che abbiamo chiamato rototraslazione, così combinando una simmetria assiale e una traslazione si ottiene una nuova trasformazione, più generale, inversa (cioè che inverte l'orientazione). Eccone un esempio:

Una trasformazione di questo tipo si chiama glissosimmetria (astenersi dai commenti, per favore; c'è chi le chiama glissoriflessioni, chi antitraslazioni, chi simmetrie con scorrimento — a me alle superiori insegnarono il termine glissosimmetria, che quindi è Quello Giusto per definizione).

Esiste un teorema simpatico che ci fa capire come le cose non possono diventare mai troppo complicate: dice che ogni isometria è la composizione di al più 3 simmetrie assiali.

Prima di parlare del gruppo delle isometrie, col quale possiamo finalmente fare una prima geometria, facciamo ancora una considerazione sulle simmetrie assiali. Esiste un altro teorema simpatico che dice che una qualunque isometria può essere decomposta in traslazione più rotazione, se diretta, oppure traslazione più rotazione più simmetria, se inversa, dove il centro di rotazione e l'asse di simmetria possono essere scelti a piacere. Quindi, per quanto riguarda le rotazioni, non abbiamo bisogno di scriverne le equazioni per ogni centro, ma ci bastano le equazioni di quelle aventi il centro dell'origine (che abbiamo già scritto).

Per le simmetrie vale la stessa cosa: non abbiamo bisogno di scriverne le equazioni per ogni possibile posizione che può assumere l'asse di simmetria, ma ci basta una sola equazione. Prendiamo quindi quella della simmetria avente come asse di simmetria l'asse delle x; la sua matrice associata è:

Ora passiamo alle isometrie.

Buon anno

Erlangen 1872 — Componiamo

Dopo aver definito le traslazioni e le rotazioni, ci potrebbe venire voglia di combinarle insieme. Che succede se applichiamo una rotazione e una traslazione a un punto (o a una figura)? Possiamo farlo nell'ordine che ci pare? Che trasformazione otteniamo?

Questa figura (complicata, sì) ci fa capire che la composizione di una rotazione e una traslazione non è commutativa. Proviamo a capire: il percorso con le figure blu ci mostra che la figura rossa viene prima ruotata di un certo angolo, poi traslata secondo un certo vettore. Il percorso con le figure verdi invece ci mostra la figura rossa che prima viene traslata, poi ruotata. Come si vede, i due percorsi non terminano sulla stessa figura: quindi bisogna stare molto attenti all'ordine in cui vengono applicate le trasformazioni.

In realtà, però, non esiste un insieme delle traslazioni+rotazioni, diverso da quello delle rotazioni+traslazioni: la figura qua sotto mostra come sia possibile arrivare alla stessa figura applicando, in un caso, prima una traslazione e poi una rotazione, in un secondo caso invece applicando prima una rotazione e poi una traslazione (diversa dalla precedente, naturalmente).

Quindi esiste un unico gruppo che contiene tutte le possibili composizioni di traslazioni e rotazioni. Questo gruppo, detto delle isometrie dirette (o delle rototraslazioni), contiene i due gruppi di rotazioni e traslazioni (che si dicono essere sottogruppi del gruppo più grande).

La matrice associata a queste trasformazioni è la seguente:

Manca ancora poco per poter parlare della prima geometria.

L'aquila

Erlangen 1872 — Rotazioni

Parliamo di rotazioni intorno all'origine.

Anche la rotazione è una trasformazione del piano, ed è certamente diversa da una traslazione. Cioè: è impossibile, anche utilizzando un numero qualsiasi di traslazioni, ottenere una rotazione. Capire il perché è molto semplice: nella traslazione tutti i punti si spostano, non ce n'è nemmeno uno che rimane fermo. Nella rotazione, invece, esiste un punto che sta fermo: il centro della rotazione. Nel linguaggio delle trasformazioni i punti che rimangono invariati sotto l'azione di una trasformazione si dicono punti uniti.

Quindi le rotazioni non stanno all'interno del gruppo delle traslazioni. A loro volta, però, esse formano un gruppo. Infatti esiste l'elemento neutro, che è la rotazione di un angolo nullo, ed esiste l'inverso: la rotazione nel verso opposto. Si adotta la convenzione di far corrispondere agli angoli positivi le rotazioni in senso antiorario, e agli angoli negativi quella in senso orario. La matrice associata a una rotazione in senso antiorario intorno all'origine di un angolo α è la seguente:

Stiamo sempre utilizzando la notazione utilizzata per le traslazioni, e cioè stiamo (per ora misteriosamente) associando a un punto del piano le coordinate (x,y,1) e non (x,y), come normalmente si fa.

Concludendo: il gruppo delle rotazioni e quello delle traslazioni sono due gruppi diversi. Entrambi danno luogo a due geometrie che, però, sono ancora troppo magre. Dobbiamo ingrassarle ancora un pochino.

Erlangen 1872 — Equazioni

Se noi ci mettiamo sul piano cartesiano, possiamo anche scrivere le equazioni delle trasformazioni geometriche. Per esempio, se si indica il vettore v di una traslazione mediante le sue componenti lungo gli assi cartesiani (e cioè v=(a,b)), allora l'equazione della traslazione di vettore v può essere scritta semplicemente in questo modo:

T(x,y) = (x+a,y+b).

Ora complichiamo le cose semplici. Gli studenti universitari imparano presto che ciò che i professori chiamano geometria è in realtà algebra lineare, almeno per qualche mese. Quella scritta sopra è, in effetti, una trasformazione lineare. Bene, ad ogni trasformazione lineare è associata una matrice, oggetto scomodo e dalle proprietà misteriose. In forma matriciale la semplice equazione scritta sopra diventa così:

Il fatto che il punto di coordinate (x,y) sia diventato (x,y,1) è dovuto a due considerazioni. La prima è che così l'operazione con le matrici funziona, altrimenti non si riuscirebbe a ottenere come risultato (x+a,y+b). La seconda la facciamo più avanti.

Diciamo dunque che la matrice associata alla traslazione di vettore v(a,b) è la seguente:

Quindi lo studio delle proprietà delle traslazioni potrebbe essere fatto analizzando questo tipo di matrici (ma noi non lo facciamo). E anche il gruppo delle traslazioni diventa il gruppo delle matrici di questo tipo, mentre la composizione di traslazioni diventa la moltiplicazione righe per colonne delle matrici.

Ma lasciamo queste cose agli studenti universitari di geometria, e passiamo ad altre trasformazioni.

Teach and Learn

Erlangen 1872 — Traslazioni

Vediamo di applicare quanto abbiamo detto alla geometria. Il nostro insieme è l'insieme dei punti del piano; una trasformazione è una generica macchinetta che prende un punto e gli cambia posizione, seguendo certe regole, naturalmente.

Bene, prendiamo le macchinette-trasformazioni e le mettiamo dentro a un insieme (infinito, naturalmente). Poi definiamo un'operazione su questo insieme, e la chiamiamo composizione. La composizione di due trasformazioni a e b è semplicemente quella trasformazione che si ottiene applicando nell'ordine prima a e poi b. Tutto qua.

L'unica cosa strana è che questa operazione non agisce su numeri, come normalmente ci si aspetta da un'operazione come si deve, ma agisce su trasformazioni geometriche.

Esempio: le traslazioni. Tutti quanti dovrebbero conoscere il termine: una traslazione è una trasformazione del piano che prende tutti i punti e li sposta di una distanza fissa nella medesima direzione.

La figura rossa viene trasformata in quella blu (il che significa che ogni punto della figura viene trasformato, naturalmente). Non è che gli altri punti siano fermi, beninteso. La traslazione agisce su tutti i punti del piano: noi ne abbiamo evidenziati alcuni, formanti una figura, e abbiamo analizzato cosa è successo a quelli.

Primo fatto: sulle traslazioni è possibile effettuare una operazione, quella che abbiamo chiamato composizione. Comporre due traslazioni significa applicarne prima una e poi l'altra. In questo caso non è importante specificare l'ordine, ma con altri tipi di trasformazioni lo sarà (questo significa che, in generale, la composizione non è una operazione commutativa). Per trovare il risultato della composizione ci basta sommare i due vettori, come abbiamo imparato a fare alle medie (con la regola del parallelogrammo, per esempio).

Ecco, in questa figura si vede la composizione di due traslazioni (indicate con le frecce tratteggiate), che possono essere viste come un'unica traslazione (indicata con la freccia continua). In alto, i due vettori corrispondenti alle due traslazioni vengono sommati con la regola del parallelogrammo, e il risultato è proprio il vettore che congiunge la figura rossa con quella verde, in basso.

Possiamo parlare di gruppo delle traslazioni? Per farlo, dobbiamo verificare che esista l'elemento neutro e che per ogni traslazione esista quella opposta. Allora, l'elemento neutro è la traslazione di vettore nullo, cioè la traslazione che lascia tutto fermo. L'opposto, invece, è quella traslazione che si ottiene girando il vettore: mettendo cioè la punta al posto della coda, e viceversa.

Quindi le traslazioni formano un gruppo. Possiamo già parlare di geometria, secondo Klein? In teoria potremmo, in pratica però questa geometria è un po' troppo povera: bisogna allargare un po' di più l'insieme delle operazioni per poter ritrovare una geometria ben nota.

Erlangen 1872 — Invarianti

Un invariante è semplicemente qualcosa che rimane costante. E fin qua.

Per capire qualcosa di più, dobbiamo tener presente che il concetto di invariante deve essere associato a quello di trasformazione. In pratica: la trasformazione mescola apparentemente gli oggetti di cui disponiamo, ma sotto sotto c'è qualcosa che rimane fisso. Si tratta di scoprirlo, e il gioco è fatto.

Giochino: abbiamo una scacchiera 8×8, e la vogliamo ricoprire con delle tessere del domino, di dimensione 1×2. Siamo capaci? Spero di sì, basta provare: in ogni riga mettiamo quattro tessere e siamo a posto. Bene, ora tagliamo via dalla scacchiera due caselle d'angolo opposte. Siamo ancora in grado di ricoprire la scacchiera con le tessere di prima? Se proviamo, non ci riusciamo. Ma, anche provando per molto tempo, non riusciremmo a verificare tutte le possibili configurazioni di tessere; però possiamo dimostrare l'impossibilità.

Indichiamo con n il numero di caselle nere visibili (cioè non coperte da nessuna tessera del domino), e con b il numero di caselle bianche visibili. Chiamiamo d la differenza n-b. Ora prendiamo la scacchiera completa: essa contiene 32 caselle bianche e 32 caselle nere, quindi d = 0. Che succede ogni volta che posizioniamo una tessera del domino?

Succede che copriamo una casella bianca e una casella nera, quindi sia n che b diminuiscono di 1; però la differenza d non varia, perché (n-1) - (b-1) è uguale a n-b. Quindi comunque noi posizioniamo una tessera del domino, la quantità d rimane costante. Ecco il nostro invariante.

Ora pensiamo alla scacchiera senza due caselle d'angolo. Se ci pensiamo un attimo, ci rendiamo conto del fatto che due caselle d'angolo hanno lo stesso colore: se le togliamo, il numero di caselle bianche sarà diverso da quello di caselle nere (diciamo di aver tolto due caselle bianche: in questo caso n-b = 2 — se togliamo due caselle nere allora n-b = -2). Ecco il motivo per cui è impossibile ricoprire questa scacchiera con le tessere del domino: il posizionamento di una tessera non fa variare d, che rimarrà sempre uguale a 2 (oppure a -2), eppure noi vorremmo arrivare a una situazione in cui tutte le caselle sono state coperte, cioè d = 0. Impossibile.

Gli invarianti sono bellissimi.

Erlangen 1872 — Gruppi

Un gruppo è una struttura algebrica caratterizzata da una operazione binaria associativa, dotata di elemento neutro e per la quale ogni elemento della struttura possiede elemento inverso.

Ecco, già dalla definizione si capisce che quello di gruppo è un concetto un po' più complicato.

Partiamo dall'inizio: struttura algebrica lo possiamo tradurre con mucchio di roba. Non specifichiamo altro: è un insieme di oggetti matematici che servono a qualcosa, il cosa è spiegato in seguito dalle proprietà che devono essere soddisfatte dagli oggetti.

Operazione binaria associativa è abbastanza facile: si tratta di una operazione che prende due elementi del gruppo e ne produce un terzo. Se pensiamo alle normali operazioni che conosciamo, va bene. Dobbiamo però tenere presente che il concetto di gruppo è molto generale, e quindi l'operazione potrebbe non essere una operazione tra numeri. Insomma, il gruppo è un insieme di oggetti, che potrebbero anche non essere numeri, ma sui quali si deve poter operare. L'operazione deve poi essere associativa, cioè deve essere una operazione decente. Se indichiamo l'operazione col generico simbolo ∗, la proprietà associativa è questa:

a∗(b∗c) = (a∗b)∗c.

Un esempio di operazione non associativa? Eccolo qua: la media tra due numeri. Se a∗b è uguale alla media tra a e b (cioè (a+b)/2) allora ci basta un esempio per capire che non gode della proprietà associativa: 1∗(2∗3) = 1∗2.5 = 1.75, mentre (1∗2)∗3 = 1.5∗3 = 2.25.

Elemento neutro è molto semplice: è come 1 per la moltiplicazione o 0 per l'addizione; deve cioè esistere un oggetto, all'interno del gruppo, il quale non produce effetti se inserito nell'operazione. In simboli, se si indica con e l'elemento neutro, questo è tale per cui:

a∗e = e∗a = a.

Arriviamo all'inverso di un elemento. L'inverso di a si indica con -a ed è tale per cui:

a∗(-a) = (-a)∗a = e.

Esempio: se consideriamo la somma di due numeri, abbiamo che l'elemento neutro è lo 0, e l'inverso di a è quel numero, che si indica con -a, tale per cui a + (-a) = 0. Insomma, l'inverso di 3 è -3, quello che normalmente si chiama opposto.

Se invece consideriamo il prodotto di due numeri, in questo caso l'elemento neutro è 1, e l'inverso di a è quel numero, che si indica con 1/a, tale per cui a × (1/a) = 1. Insomma, l'inverso di 3 è 1/3, quello che normalmente si chiama reciproco.

Basta, il gruppo non ha altre proprietà, queste sono quelle di base.

Naturalmente l'astuto lettore avrà notato che se si prendono, ad esempio, i numeri naturali, gli esempi fatti sopra non funzionano: -3 e 1/3 non appartengono all'insieme dei numeri naturali. Quindi quando si definisce un gruppo bisogna specificare bene anche l'insieme che stiamo considerando, e non solo l'operazione. Dunque potremmo dire che l'insieme dei numeri interi, con l'operazione di somma, è un gruppo. Oppure che l'insieme dei numeri razionali senza lo zero, con l'operazione di moltiplicazione, è un gruppo. Insomma, occorre che l'insieme considerato sia chiuso rispetto all'operazione, il che significa che ogni operazione tra due elementi qualsiasi deve dare un risultato che appartiene ancora all'insieme.

Se si è precisi, tutto fila liscio.

Erlangen 1872 — Trasformazioni

Si parlava di studio delle proprietà di uno spazio che sono invarianti rispetto ad un gruppo di trasformazioni. Allora, quando diciamo spazio possiamo intendere anche piano, e questo non perché i matematici non conoscano la differenza tra le due parole, ma perché con spazio si intende un po' tutto. Insomma, quello che la gente normale considera spazio, i matematici lo chiamano spazio a tre dimensioni. E così il piano diventa lo spazio a due dimensioni, la retta lo spazio a una dimensione, e abbiamo spazio (appunto) per generalizzare a quattro, cinque, n dimensioni.

Fermiamoci a due dimensioni, che i disegni sono più facili.

Il piano è fatto di punti, che ora dobbiamo immaginare come mobili: come la superficie del mare, per esempio, ma di un mare senza onde. Immergiamo la mano e diamo una mescolata: abbiamo effettuato una trasformazione geometrica. Ovvero abbiamo preso dei punti e li abbiamo spostati da un'altra parte. Un oggetto matematico che prende i punti del piano e li muove si chiama trasformazione geometrica.

Esempi pratici: scriviamo le formule che ci interessano su un foglio, lo inseriamo in un fotocopiatore e produciamo un meraviglioso francobollo che contiene tutto quello che ci serve. Abbiamo stabilito una trasformazione geometrica tra i punti del foglio e quelli della fotocopia (non importa molto se i due fogli sono diversi, possiamo immaginarli come sovrapposti e trattarli come uno solo).

Oppure: un telefilm in formato 4:3 viene proiettato su un televisore in formato 16:9 senza bande nere ai lati: il quadro è deformato, e abbiamo fatto una trasformazione che prende i punti del piano (dello schermo televisivo) e li dilata.

E infine: prendiamo un foglio e, semplicemente, lo capovolgiamo. Ciò che era in alto ora è in basso, e viceversa: abbiamo nuovamente spostato i punti del piano; ma non tutti, se ci pensiamo bene: il centro del foglio, ad esempio, è rimasto fermo.

E così abbiamo chiarito il primo termine: trasformazione.

Erlangen 1872 — Che cosa è la geometria?

Che cosa è la geometria? Se lo chiediamo a un bimbo delle elementari, probabilmente ci risponderà che non lo sa spiegare bene, perché a volte si confonde un po' con la geografia. Un ragazzino delle medie ci risponderà che è quella materia scolastica in cui si studiano le figure e le misure. Se arriviamo alle superiori, un ragazzo del biennio si metterà le mani nei capelli pensando alla geometria euclidea, ai suoi teoremi e alle sue dimostrazioni senza numeri. Un ragazzo del triennio farà altrettanto, pensando invece alla geometria analitica e alle sue formule. Infine, uno studente universitario risponderà che la geometria è la materia più difficile del primo anno, perché è piena di formule, matrici, determinanti, autovettori, trasformazioni lineari, ma di figure non se ne vede una.

Se andiamo a dare un'occhiata alla voce Geometria di Wikipedia, troviamo elencate almeno dieci geometrie diverse, tanto per dire.

Poi nel 1872 è arrivato Felix Klein, che ha proposto di vedere tutte queste geometrie da un unico, nuovo, punto di vista. Nel suo programma di Erlangen Klein ha spiegato che una geometria consiste nello studio delle proprietà di uno spazio che sono invarianti rispetto ad un gruppo di trasformazioni.

Eh?, diranno tutti gli studenti di ogni ordine e grado.

Si tratta di capire i termini della questione, spiegare cosa significano invariante, gruppo, trasformazione. Poi è facile.

Carnevale della Matematica #28

One would be hard put to find a set of whole numbers with a more fascinating history and more elegant properties surrounded by greater depths of mistery — and more totally useless — than the perfect numbers.

Martin Gardner

La bellezza dei numeri perfetti è stata ammirata, anche con una sorta di timore mistico, dai matematici di tutti i tempi.

I pitagorici, ad esempio, associavano il numero 6 al matrimonio, alla salute e alla bellezza.

Filone di Alessandria, nel primo secolo, associò 6 alla perfezione e al movimento dei corpi organici, i quali possono spostarsi lungo sei direzioni (alto, basso, avanti, indietro, destra, sinistra). Oggi parleremmo di gradi di libertà di un corpo rigido.

Nicomaco, nella sua Introduzione all'aritmetica, scritta intorno all'anno 100, osserva l'armonia dei numeri perfetti, in equilibrio tra i numeri difettivi e i numeri abbondanti, e fa notare come 6, 28, 496 e 8128 siano i soli numeri perfetti compresi negli intervalli di estremi 1, 10, 100, 1000 e 10000. Inoltre, essi terminano alternativamente con la cifra 6 oppure con la cifra 8.

Sant'Agostino, vissuto a cavallo tra il quarto e quinto secolo, considerava il 6 come un numero veramente perfetto: Dio creò il mondo in 6 giorni proprio per dimostrare la perfezione della sua opera. Allo stesso modo Alcuino di York, vissuto nel settimo secolo, notava come la cosiddetta seconda origine fosse invece imperfetta, dato che si è basata sul numero 8, un numero difettivo (otto erano infatti gli uomini contenuti nell'arca di Noè: Noè stesso, i suoi tre figli e le loro quattro mogli).

Roswitha di Gandersheim, badessa del convento di Gandersheim, in Sassonia, considerata la prima poetessa tedesca (anche se scriveva solo in latino), in uno dei suoi drammi, intitolato Sapientia e scritto nel decimo secolo, elenca i primi quattro numeri perfetti.

I numeri perfetti erano così importanti per gli ebrei che il rabbino Josef ben Jehuda Ankin suggerì, nel suo libro dedicato alla cura dell'anima e scritto verso la fine del dodicesimo secolo, di studiare le loro proprietà.

Ericio Puteano, un enciclopedista, nei suoi scritti del 1640 riferisce l'associazione tra Venere e il numero 6, in quanto formato dalla diade (femminile e pari) e la triade (maschile e dispari).

Nei secoli seguenti i matematici hanno continuato a studiare le proprietà dei numeri perfetti, raccogliendo un notevole numero di risultati (e anche di congetture errate).

Se indichiamo con σ(n) la somma dei divisori di n (compresi 1 e n stesso), allora un numero N si dice perfetto se σ(N) = 2N. Se invece σ(N)<2N, allora il numero si dice difettivo, mentre se σ(N)>2N, allora il numero si dice abbondante.

Se un numero N è perfetto, allora la somma dei reciproci dei suoi divisori è sempre uguale a 2.

Euclide, nella proposizione 36 del libro IX degli Elementi, afferma (in forma un po' più discorsiva) che se 2ⁿ-1 è primo, allora N = 2^n-1(2ⁿ-1) è perfetto. Quindi la ricerca dei numeri perfetti è legata alla ricerca di numeri primi nella forma 2ⁿ-1, detti numeri di Mersenne.

Ogni numero primo di Mersenne genera un numero perfetto, e viceversa ogni numero perfetto genera un primo di Mersenne. Questo risultato è noto come teorema di Euclide-Eulero.

Il criterio di Cataldi-Fermat può essere d'aiuto: se 2ⁿ-1 è primo, allora n è primo.

Eulero, in un teorema pubblicato dopo la sua morte, ha dimostrato che se N è un numero perfetto pari, allora esso può essere scritto nella forma N = 2^n-1(2ⁿ-1), dove 2ⁿ-1 è primo.

Se N è un numero perfetto pari, allora è anche un numero triangolare.

Se N è un numero perfetto pari (e quindi può essere scritto come 2^n-1(2ⁿ-1)), allora n = 1³ + 2³ + … + (2^(n-1)/2-1)³.

Sempre utilizzando la notazione del teorema precedente, se N è un numero perfetto pari allora, scritto in base 2, possiede 2n-1 cifre; le prime n sono uguali a 1, le ultime n-1 sono zero.

Ogni numero perfetto pari termina con la cifra 6 o con la cifra 8.

Se si sommano le cifre di un numero perfetto pari (escluso 6) e si ripete il processo fino ad avere una sola cifra, si ottiene 1.

Per quanto riguarda i numeri perfetti dispari, non sappiamo quasi niente. Non sappiamo nemmeno se esistono; forse non esistono. Se esistono, sono sicuramente maggiori di 10³⁰⁰, forse anche di 10⁵⁰⁰.

Concludiamo la storia con un'affermazione di Sylvester, del 1888: a prolonged meditation on the subject has satisfied me that the existence of any one such [odd perfect number] — its escape, so to say, from the complex web of conditions which hem it in on all sides — would be little short of a miracle.

Tutto questo, comunque, è per introdurre il Carnevale della Matematica numero 28. Il prossimo Carnevale-perfetto sarà il numero 496, che si terrà il 14 dicembre 2051, non si sa ancora dove.

Il prossimo Carnevale, invece, sarà il numero 29 e verrà ospitato dai Rudi Matematici.

E ora andiamo a incominciare.


.mau., per quanto riguarda la categoria Povera matematica, ha scovato due errori: in Fanno sbagliare i conti già ai piccoli si vede come sia difficile fare una sottrazione, mentre in Chilometro e mezzo quadrato fa notare come non sia proprio corretto confondere misure lineari con misure di superficie.

Per la categoria link, il nostro ci segnala il CD con la raccolta completa dei libri di Martin Gardner dallo Scientific American a prezzo scontato, mathURL e asciiTeX, due sistemi per inserire formule matematiche nei propri siti e math@stackexchange, una nuova community matematica in via di sviluppo (e in inglese, naturalmente).

Per la categoria recensioni, ecco due libri: Il matematico curioso, che cerca di mostrare come la matematica spunti dappertutto, se la si sa vedere; Mathematical Recreations, storia della matematica ricreativa a.G. (cioè avanti Gardner).

Per la categoria giochi, il Futoshiki: un sudoku dove i numeri sono davvero numeri e non segnaposto.

Per la categoria io, un importante annuncio: Ho anch'io un numero di Erdős!

Infine, per la mega-categoria Il Post (ovvero un altro blog matematico), abbiamo: Il paradosso di san Pietroburgo: da un banale gioco di testa o croce non solo si può arrivare a una vincita potenzialmente infinita, ma addirittura si ha che la vincita media è infinita! Proseguiamo poi con Dal paradosso dell'Alabama ai deputati frazionari: il metodo proporzionale sembra essere il più equo per suddividere i deputati da eleggere; ma anche in questo caso sorgono dei paradossi. Poi abbiamo Parole matematiche: parabola: che cosa hanno in comune i racconti evangelici con l'antenna satellitare? E ancora  Il teorema di Pitagora: il teorema più famoso della geometria merita indubbiamente una trattazione a sé. Seguono Paul Erdős: i matematici sono spesso dipinti come persone piuttosto strane, anche se in genere non pericolose — beh, Erdős ha pienamente diritto di essere inserito in questa categoria; La funzione base-13 di Conway: un post da leggere in parallelo a Continuità (pubblicato qui): noi siamo abituati a pensare alle funzioni come qualcosa di disegnabile, ma non è che sia sempre così, anzi — ecco un esempio non molto noto di funzione assolutamente incredibile; Parole matematiche: prodotto, fattore: due parole al prezzo di una: stavolta l'origine è latina e non greca, e soprattutto hanno in comune qualcosa in più di quanto si potrebbe pensare a prima vista; La serie armonica: molte successioni hanno una somma infinita, altre hanno una somma finita — la serie armonica va sì all'infinito, ma così piano che uno magari non se ne accorge nemmeno. Infine, Problemini matematici ferragostani: per una volta, anche il blog di matematica si prende qualche libertà.

Ho scritto infine, ma in realtà non è così: il 9 agosto ha iniziato a girare la notizia che forse è stato dimostrato uno dei problemi del millennio, la congettura più importante nel campo dell'informatica; pare cioè che sia vero che P != NP: .mau. ne ha parlato in P != NP (o no?), fornendo anche una spiegazione del problema che vede coinvolti Gastone, Paperino e Qui, Quo, Qua.


Dioniso, continuando la trattazione già pubblicata nello scorso carnevale, ci propone l'appendice numero 1 e la numero 2 alla sua serie Chi vincerà il mondiale del 2014? Una questione di Logica intuizionista? Infine, un approfondimento alla appendice 2: Tentativo di dimostrazione che nella logica intuizionista (I → ¬¬I), ma non (¬¬I → I). Qui si può leggere o scaricare l'opera completa.


Gianluigi Filipelli ha mandato una lista dei suoi post corredati tutti con un'ottima e abbondante descrizione: lascio quindi la parola a lui per il commento ai suoi pezzi. Dal suo blog personale, dropsea, abbiamo:

Calcolare le equazioni con Geogebra: due applet di Geogebra realizzate da due gruppi di miei ex-studenti del primo superiore: Stefano, Davide, Fabio, Alessandro. Un modo per risolvere le equazioni come intersezione tra figure geometriche.
Un problema pitagorico: un altro post realizzato grazie al contributo delle applet di miei ex-studenti dell'ultimo anno scolastico. In questo caso Federica, Hazel, Giuditta, Stefano, Matteo hanno risolto un problema pitagorico che ho trovato sul blog di Annarita utilizzando Geogebra.
Integrali e polilogaritmi: una collega mi ha proposto un integrale. Ho provato a risolverlo, ma vedendo che arrivavo a un certo punto e mi bloccavo, ho... barato usando Wolfram Alpha... Ed ecco la sorpresa!

Da Science Backstage, invece, Gianluigi propone i seguenti post:

L'algoritmo del destino: il mitico John Conway, oltre al famoso gioco della vita, ha realizzato anche molte altre cose nell'ambito della ricerca matematica ricreativa. In particolare un algoritmo con il quale è in grado di calcolare a mente il giorno della settimana corrispondente a una certa data. &Ergave; stato, però, recentemente proposto un aggiornamento da parte di Chamberlain Fog, e quindi anche di questo si va a discutere nell'articolo.
Scalando il Tourmalet: di tutti i post dedicati al Tour de France, questo è quello che contiene esplicitamente la matematica, grazie alla pendenza di una retta.
La storia di Achille e della tartaruga: un nuovo Rompicapo, tra fisica e matematica. Se nella prima parte si affronta il famoso paradosso di Zenone dal punto di vista della fisica, nella seconda si esamina un nuovo paradosso che coinvolge Achille e la tartaruga, questa volta elaborato dal grande Carroll.
Terne non pitagoriche, aree intere: sappiamo tutti che le terne pitagoriche altro non sono che tre numeri interi che verificano il Teorema di Pitagora. È allora possibile trovare, data l'ipotenusa, due altri cateti non necessariamente naturali che danno come area del triangolo un numero intero? Provo a rispondere con questo piccolo problemuccio geometrico. Alla fine anche una applet Geogebra (giusto per non farsi mancare niente!)


Peppe Liberti ha parlato di Bessel e delle sue funzioni in Funzioni sulla sabbia, e poi si è lamentato di un certo uso della matematica in Cosa non sopporto della matematica (basta la frase “i misteri della scienza” per spiegare contro cosa se la prende Peppe?)


Maurizio ha poi scritto Ma quasi tutti sanno che…, dove si può trovare un'applicazione del principio di induzione per dimostrare una proprietà della somma dei cubi di tre numeri maturali consecutivi, e Joseph Ludwig Raabe, un breve profilo del matematico svizzero con un'applicazione del suo criterio di convergenza per le serie numeriche.


Claudio Pasqua, da Gravità Zero, partecipa con il post intitolato “Sua Altezza” Talete di Mileto, in cui riporta e amplia un articolo comparso su MondoErre riguardante il matematico e filosofo greco. Il post si conclude con un semplice problemino, intitolato L'elefante e il topolino (semplice ma non stupido, non fatevi ingannare…).


Annarita Ruberto ci manda, come al solito, una lunghissima serie di contributi. Per quanto riguarda la storia della matematica e la divulgazione, abbiamo:

Talete: Il Fondatore Della Matematica Greca [Scheda Storica]: una scheda storica sul grande Talete.

Perché Non Usiamo Più I Numeri Romani?: l’articolo riporta un brano estratto da libro di Clifford Pickover Le Meraviglie dei Numeri, in cui un ragazzo pone la domanda “Perché non usiamo più i numeri romani?” al dottor Googol. Un “Googol” è un numero pari a 10mila decaexilioni, ovvero un numero intero esprimibile con 1 seguito da 100 zeri. Ma il Dottor Francis O. Googol «è un personaggio di cui Clifford Pickover narra le avventure matematiche». Sarà, infatti, il Dottor Francis O. Googol a «trasportarci verso nuovi mari, rendendo più profonde le acque e allargando gli orizzonti». Nel brano sono contenuti due rompicapo con i numeri romani.

Perché Si Usa IIII E Non IV Sui Quadranti Di Alcuni Orologi?: l'articolo nasce da una domanda posta da un lettore in un commento al post "Perché non usiamo più i numeri romani?".

I Numeri Di Mozart: che la musica di Mozart avesse a che fare con i numeri e con la matematica è cosa risaputa. Grazie a un progetto promosso da alcuni insegnanti inglesi si è scoperto, infatti, che ascoltare la musica mozartiana migliora le performance degli studenti in ambito matematico. L'articolo riporta un brano tratto dalla Magia dei Numeri di Clifford Pickover.

L'Eredità Arabo-Indiana [Scheda Storica]: il contributo dei matematici indiani e di quelli arabi allo sviluppo del pensiero matematico universale.

Il Problema Di Euler: problema contenuto nella Introduzione all’algebra di Euler, che impressionò Stendhal.

Leonardo Pisano (detto Fibonacci).

Per quanto riguarda la didattica, annarita ha scritto:

La Tavola Pitagorica E I Numeri Quadrati: un contributo di Bruno Berselli per Matem@ticaMente. Sappiamo che solitamente la Tavola pitagorica viene presentata come uno schema quadrato di 10×10 o 12×12. Può allora essere interessante chiedersi se essa abbia qualche caratteristica non ovvia legata ai numeri quadrati. Ne esiste una, in effetti, pur non essendo l’unica, che viene analizzata nell'articolo.

Problema Con Quadrato, Rettangolo E Triangolo Rettangolo, Risolto Con GeoGebra.


Paolo Pascucci ha preparato una serie di interventi dal titolo Aritmetica e Cervello: l'aritmetica è connaturata ai cervelli di molti animali, oppure no? Ecco qua il primo post, il secondo e il terzo.


Popinga partecipa con un solo, denso, contributo: La matematica visionaria di Yi Sang. L’opera poetica del coreano Yi Sang, di cui ricorre quest’anno il centenario della nascita, è caratterizzata da versi liberi, originali grafie, giochi di parole, che disorientano il lettore, allora come oggi. Spesso il carattere e l’impaginazione hanno un aspetto matematico, evocando formule numeriche e combinatorie, con simboli, parentesi, punti, deliberata sovversione degli spazi. Inoltre i testi della traslitterazione coreana rivelano un gioco occulto di regole, di ripetizioni, di simmetrie e di giochi di specchi impossibili da rendere nel nostro alfabeto.


Questo mese abbiamo una new entry: si tratta di Melassa, che ha scritto un post intitolato Il soggetto noto. Il matematico Oliver Byrne diede alle stampe nel 1847 The first six books of the elements of Euclid: in which coloured diagrams and symbols are used instead of letters for the greater ease of learners, definito dall’American Scientist il più bel libro di matematica di tutti i tempi. Byrne concepì questa edizione di Euclide come un sistema completamente nuovo per imparare la geometria, riducendo al minimo il testo scritto e dando forma visuale alle informazioni. Il suo testo da un punto di vista di didattica della matematica è assolutamente inutile, ma le sue composizioni geometriche anticipano l’arte di Mondrian e di tanti altri pittori del Novecento.


I Rudi Mathematici ci scrivono direttamente dalla loro riunione di comitato di redazione, proponendoci i seguenti contributi: uno dei migliori compleanni mai usciti dalla penna di Alice, quello del misconosciuto Robert Hooke, a cui fa buon seguito uno dei migliori Zugzwang! (si sente che stanno facendo la riunione in terra tedescofona?), i Secondi scivolosi secondo il GC. Segue poi la soluzione al quiz pubblicato su Le Scienze (i Rudi si chiedevano se io volessi pubblicarlo sul carnevale della matematica, e hanno quindi aggiunto la seguente descrizione: considera che l'occasione di vedere Alice in costume da bagno è davvero rara. Vedete voi se dare un'occhiata o no). Segue poi un bel post, che ha fortemente voluto Rudy: si tratta di indicare i libri di argomento (più o meno) matematico per l'estate, per le vacanze, per la vita e per tutto il resto. A dire il vero hanno rubato l'idea ad un blog confratello (quello di Daniela Ovadia), ma tanto l'idea l'aveva già rubata anche lei… Si continua poi con altri due compleanni: quello di P.A.M. Dirac, sempre dalla penna di Alice, e quello del glorioso Erwin Schroedinger. Ma a tenere un blog son buoni tutti: i nostri sono anche arrivati a pubblicare il numero 139 di una prestigiosa rivista di matematica ricreativa; dite voi se è poco.

Il Carnevale finisce qui: divertitevi.

Aggiornamento

Grazie a .mau. che ha tirato fuori l'argomento, e grazie a questo sito di ricerche di collaborazioni, posso gioiosamente annunciare che il mio numero di Erdős è (minore o uguale a) 5.