Si tratta di fare un passo ardito. Ma, per capire bene, bisogna fare qualche calcoletto.
Prendiamo l'equazione di una retta, per esempio y=x: è una equazione molto semplice, che rappresenta la bisettrice del primo e del terzo quadrante.
Prendiamone un'altra, per esempio y=2x-1. Se le rappresentiamo sul piano, otteniamo questo grafico:
Sono due rette secanti; se vogliamo trovare le coordinate del loro punto di intersezione, dobbiamo risolvere il sistema tra le due equazioni, che è il seguente:
Con una semplice sostituzione si trova la soluzione, che è proprio x=1, y=1, come si vede anche dal grafico.
Bene: rifacciamo i calcoli in coordinate omogenee.
Come si trasformano le equazioni? Non è difficile: ogni volta che si trova una x si sostituisce x/z, e ogni volta che si trova una y si sostituisce y/z. Quindi le equazioni delle due rette diventerebbero:
E ora il passo ardito: eliminiamo i denominatori senza porci troppi problemi, e rimettiamo a sistema il tutto;
Cosa è successo? Prima di tutto l'equazione di una delle due rette è cambiata, e in secondo luogo abbiamo un sistema in tre equazioni e due incognite. Vediamo di capirci qualcosa.
Primo fatto: se l'equazione originale non aveva termine noto (si dice che era omogenea), allora trasformandola in coordinate omogenee non cambia. Infatti senza termini noti si osserva che z è un denominatore comune, che si può togliere senza scrupoli (se per caso capita da queste parti uno studente di prima superiore: normalmente questa semplificazione è considerata un errore, servono le condizioni di esistenza, eh).
Se l'equazione originale invece aveva termine noto (cioè era non omogenea), la trasformazione in coordinate omogenee la fa diventare omogenea (guarda un po'). Insomma, il termine noto acquisisce una z.
Secondo fatto: un sistema di due equazioni in tre incognite non ha un unico risultato, di solito: ci sono troppe incognite. Se proviamo a risolvere per sostituzione il sistema scritto sopra, otteniamo x=z, e non abbiamo ulteriori equazioni per determinare il valore di z. La soluzione del sistema, utilizzando queste nuove coordinate, diventa quindi (z,z,z). Dividendo tutto per z, otteniamo (1,1,1). Che, in coordinate omogenee, rappresenta il punto (1,1).
Riassunto: abbiamo effettivamente complicato le cose semplici.
Ma allora, perchè lo facciamo?
La risposta è data dal seguente esempio. Proviamo a calcolare l'intersezione tra le due rette y=x e y=x-1.
Le due rette sono parallele, quindi non hanno intersezione. Effettivamente, il sistema tra le loro due equazioni, in coordinate cartesiane, è impossibile. E quello in coordinate omogenee?
Eccolo qua:
Sostituendo x al posto di y nella seconda equazione, otteniamo z=0. Quindi questo sistema ammette soluzione! Tutte le terne del tipo (x,x,0) vanno bene. Dividendo per x, otteniamo ad esempio come soluzione il punto (1,1,0). Quindi il sistema tra le equazioni delle due rette parallele ha soluzione.
Quindi due rette parallele si incontrano in un punto. E buonanotte a Euclide.

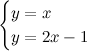

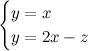

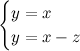
Nessun commento:
Posta un commento