Eccoci a una nuova trasformazione: la simmetria assiale.
Qui abbiamo una novità, rispetto alle traslazioni e alle rotazioni: l'orientazione della figura viene invertita. Se percorriamo in senso antiorario i vertici della figura rossa, vediamo che i vertici della figura blu vengono percorsi in senso orario, e viceversa. È come se la figura venisse staccata dal foglio, capovolta e poi riappoggiata: con le traslazioni e con le rotazioni questo non succedeva.
Le simmetrie assiali non formano un gruppo: se ne componiamo due, quello che risulta non è più una simmetria assiale (infatti se si varia l'orientazione due volte, è come se non si fosse fatto nulla: la composizione di due simmetrie assiali è una isometria diretta).
Per potere avere un gruppo bisogna allargare un po' l'insieme: assieme alle simmetrie bisogna comprendere anche le isometrie dirette. Il gruppo che si ottiene è detto delle isometrie (senza specificare se sono dirette o inverse). Proviamo a descriverlo: esso contiene, come abbiamo già visto, tutte le traslazioni, le rotazioni, e le simmetrie assiali. Contiene altro? Certamente contiene le rototraslazioni, di cui abbiamo già parlato. Le simmetrie centrali contano poco: sono in realtà rotazioni di un angolo piatto intorno a un punto. C'è altro?
Sì, come combinando una rotazione e una traslazione otteniamo una trasformazione più generale, che abbiamo chiamato rototraslazione, così combinando una simmetria assiale e una traslazione si ottiene una nuova trasformazione, più generale, inversa (cioè che inverte l'orientazione). Eccone un esempio:
Una trasformazione di questo tipo si chiama glissosimmetria (astenersi dai commenti, per favore; c'è chi le chiama glissoriflessioni, chi antitraslazioni, chi simmetrie con scorrimento — a me alle superiori insegnarono il termine glissosimmetria, che quindi è Quello Giusto per definizione).
Esiste un teorema simpatico che ci fa capire come le cose non possono diventare mai troppo complicate: dice che ogni isometria è la composizione di al più 3 simmetrie assiali.
Prima di parlare del gruppo delle isometrie, col quale possiamo finalmente fare una prima geometria, facciamo ancora una considerazione sulle simmetrie assiali. Esiste un altro teorema simpatico che dice che una qualunque isometria può essere decomposta in traslazione più rotazione, se diretta, oppure traslazione più rotazione più simmetria, se inversa, dove il centro di rotazione e l'asse di simmetria possono essere scelti a piacere. Quindi, per quanto riguarda le rotazioni, non abbiamo bisogno di scriverne le equazioni per ogni centro, ma ci bastano le equazioni di quelle aventi il centro dell'origine (che abbiamo già scritto).
Per le simmetrie vale la stessa cosa: non abbiamo bisogno di scriverne le equazioni per ogni possibile posizione che può assumere l'asse di simmetria, ma ci basta una sola equazione. Prendiamo quindi quella della simmetria avente come asse di simmetria l'asse delle x; la sua matrice associata è:
Ora passiamo alle isometrie.


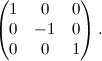
Nessun commento:
Posta un commento