Abbiamo detto che l'equazione di una conica è una generica equazione di secondo grado in due incognite:
che in coordinate omogenee diventa:
Se ora intersechiamo con la retta impropria (che ha equazione z=0), otteniamo:
che è una equazione di secondo grado facilmente risolvibile con la solita formula. Come succede per tutte le equazioni di secondo grado, sono possibili tre casi:
— due soluzioni reali distinte: in questo caso la conica ha due punti impropri diversi, e quindi è una iperbole;
— due soluzioni reali coincidenti: in questo caso la conica è tangente alla retta impropria, ed è una parabola;
— nessuna soluzione reale: ecco l'ellisse.
Insomma, le coniche si riconoscono dal tipo di intersezione che hanno con la retta impropria. O, se vogliamo, per come vanno all'infinito.
Sarà meglio fare qualche disegnino.
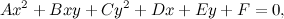
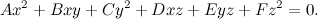
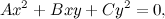
11 commenti:
Oddio, sto perdendo colpi...
...ma l'equazione:
A x^2 + B xy + C y^2 = 0
non descrive mica una curva? (in particolare una conica passante per l'origine?)
E dunque cosa significa "risolvibile con la solita formula"? Posso risolverla per x=0 o per y=0 (e allora ho sempre 0 come altro punto: la curva, per qualsiasi valore di A, B e C, passa sempre per l'origine... be', è proprio un'equazione omogenea!).
Del resto ha senso: se non sapessi (come in effetti non so) niente di geometria proiettiva, un'equazione di secondo grado in tre incognite (x, y, z) rappresenta, in casi non degeneri, una superficie nello spazio: intersecandola con z=0 (che se non so niente di geometria proiettiva è un piano nello spazio) ottengo in generale una curva (una conica, appunto), e dei punti solo nei casi degeneri (per particolari valori di A, B e C).
Insomma: dove sto (vergognosamente) sbagliando? O quantomeno fraintendendo? Di quali soluzioni parli?
Uh, ho tagliato un po' troppo, forse. Ricordati che quell'equazione proviene da un sistema, e quindi ha perso il significato geometrico (manca la z). Inoltre è una equazione in due variabili perché il sistema aveva 3 incognite ma solo due equazioni: le soluzioni che troverai saranno dipendenti da un parametro (la famosa costante semplificabile nelle coordinate omogenee).
Quindi, in pratica, devi risolvere quell'equazione ricavano x oppure y, come credi. E puoi avere tre casi:
se delta è negativo, l'equazione è impossibile - non ci sono intersezioni con la retta impropria
se delta è zero, ottieni una sola soluzione, del tipo (a,b,0). Un solo punto improprio, punto di tangenza. Questa è la parabola.
se delta è positivo, ottieni due soluzioni distinte, (1,m1,0) e (1,m2,0): due punti impropri, è la parabola.
[La z che vedi qua non c'entra niente con la z delle coordinate cartesiane nello spazio. Qua siamo sempre nel piano.]
Ti regalo due risultati simpatici (sono stati il mio "primo" teorema)
1.
Sia PQRST un pentagono convesso inscritto in una conica C del piano proiettivo. Consideriamo i punti di intersezione ABCDE delle sue diagonali e l'unica conica che passa per questi ultimi. Si indichi poi in minuscolo la polare di ogni punto rispetto alla conica in cui giace (cioè la tangente alla conica in quel punto): $a$ è la polare di $A$, ... $e$ è la polare di $E$, $p$ è la polare di $P$, ... , $t$ è la polare di $T$.
Mostrare che $p\cap t, A, q\cap r$ sono allineati, e che questa condizione di allineamento vale anche per gli altri punti (in pratica, la polare ad un punto della conica interna passa per due particolari punti di intersezione tra le polari della conica esterna): qui una figura
http://img369.imageshack.us/img369/4417/pentaggp8.png
2.
Sia $\mathcal{Q}$ una conica nel piano prioettivo reale. Siano $A,B,C$ tre suoi punti ($ABC$ è un triangolo inscritto in $\mathcal{Q}$), $a,b,c$ le polari dei lati omonimi (in tal modo $A'=b\cap c, B'=a\cap c, C'=a\cap b$ e $A'B'C'$ è un altro triangolo, stavolta circoscritto a $\mathcal{Q}$)
Mostrare che AA', BB', CC' convergono. Detto $O$ tale punto comune, qual è la polare di $O$ rispetto a $\mathcal{Q}$?
Detti $D=CC'\cap\mathcal{Q}, E=AA'\cap\mathcal{Q}, F=BB'\cap\mathcal{Q}$, mostrare che presi cinque qualunque dei punti dell'esagono formato dall'"intersezione" di $ABC$ e $D EF$ (dare nuovi nomi sta diventando confusionario, riferiamoci a un disegno) l'unica conica $\mathcal{C}$ che passa per quei 5 punti passa anche per il sesto.
Uelà!
Scusa, ma ancora non mi è chiaro.
So che z non è una coordinata spaziale nel tuo discorso, ma un'equazione è un'equazione e posso sempre interpretarla come preferisco.
E dunque
A x^2 + B xy + C y^2 = 0
è un'equazione in due incognite e dunque una curva, no?
Del resto Wolfram Alpha mi conforta: come dici tu, a seconda di delta, ci sono tre casi. Ma il punto è che il delta non dipende solo da A, B e C, ma anche da y (se ho risolto in x, da x se risolvo in y).
Insomma, quelle "due" soluzioni che trovi, (1,m1,0) e (1,m2,0), per me sono coordinate parametriche di una curva, ovvero si può scrivere m1 = m1(m2) o viceversa m2 = m2(m1). O meglio, senza supporre l'invertibilità, m1 = f1(t) e m2 = f2(t).
Forse non riesco bene a chiarire il mio dubbio...
Ti faccio un esempio: classificare la conica
x^2-3xy+2y^2+x+y+1=0.
Trasformo in coordinate omogenee:
x^2-3xy+2y^2+xz+yz+z^2=0.
Metto a sistema con la retta impropria e risolvo il sistema.
x^2-3xy+2y^2=0,
(x-2y)(x-3y)=0.
Quindi x=2y oppure x=3y. Le soluzioni del sistema sono due:
(2y,y,0),
(3y,y,0).
Che si possono scrivere come:
(2,1,0),
(3,1,0).
O anche:
(1,1/2,0),
(1,1/3,0).
Dunque la conica è una iperbole, i cui asintoti hanno pendenza:
m1 = 1/2,
m2 = 1/3.
Ho risposto?
(uhm, stavo rispondendo a un commento di hronir che mi è arrivato via mail ma non vedo qua. Boh, hronir, ci sei?)
Eccomi, ci sono: può darsi che il link a wolfram alpha non sia piaciuto a blogspot.
Cmq hai risposto, e mi hai dato ragione: x=2y e x=3y sono due rette (due "curve"), non due punti. Poi tu scegli due punti su queste rette, anzi, scegli i loro coefficienti angolari. E allora ok, si possono avrere zero, una o due rette, ma non zero, uno o due punti.
Oh, intendiamoci, uno può semplificare il linguaggio come più conveniente, ma almeno ora mi è chiaro cosa intendevi (e perché io non capivo...).
Grazie e scusa ancora l'intrusione pedantesca... :-)
Io non le vedo come due rette, perché ho in mente che in coordinate omogenee i punti dipendono da una costante arbitraria. Ma se tu, immaginando due rette, hai capito, va benissimo così :-) Con le robe all'infinito ognuno ha un suo modo di "vedere"...
Eccolo! Adesso sì, dopo questo tuo ultimissimo commento, mi è chiaro cosa mi mancava! Cosa avevo perso, perché effettivamente tu l'avevi detto, in un post precedente: che le coordinate omogenee sono definite a meno di una costante moltiplicativa!!!
In effetti quando si tratta di punti propri, questa libertà riduce i gradi di libertà da tre (le tre coordinate, la tripla di numeri) a due (che sono effettivamente i punti del piano). E la cosa che, a quanto leggo da te, si fa usualmente è fissare z ad un particolare valore, e.g. 1, così da "fissare il gauge" e ritrovare le usuali coordinate del piano senza ambiguità moltiplicative.
Il punto è che il "gauge" è fissato per un qualsiasi scelto valore di z... a meno di zero! Per z=0 il gauge non è fissato, cioè l'aver fissato z a 0 non ha assorbito l'arbitrarietà moltiplicativa. E quando volessi assorbirla, scoprirei che i punti a z=0 hanno un solo grado di libertà residuo (sono appunto una *retta* di punti (impropri) non un piano). E dunque, chiarito(mi) questo, ora mi torna che si parli di soluzioni "puntuali" (e non di curve) all'equazione da cui sono partito coi miei commenti qui.
Il punto (sottile, almeno per me che non ho mai fatto geometria proiettiva) era che fissare z ad un valore costante va bene... a patto di non scegliere zero, e che se si sceglie zero non si sta "fissando il gauge" ma si sta "approdando" da un'altra parte e soprattutto che quest'altra parte è: 1) a un solo grado di libertà e (quindi) 2) le due coordinate rimanenti x,y sono ridondanti.
Oh, chiariamoci: avevi già detto tutto tu, ma ora sono riuscito a fare meglio mente locale.
Grazie, ciao!
Oh, benissimo :-) La terza coordinata z potrebbe essere considerata anche in modo "digitale": 1=punto proprio, 0=punto improprio.
Posta un commento