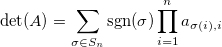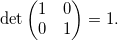Baricentro

 

“Cos'è 'sta roba?”.

“Le mediane di un triangolo si intersecano tutte in uno stesso punto che si chiama baricentro e che le divide in due parti, una il doppio dell'altra”.

“Ehhh?”.

“Il famoso teorema sul baricentro, no?”.

“Famosissimo. Però il baricentro l'ho già sentito nominare, ma in fisica”.

“Beh, la fisica è una parte della matematica che ha qualche applicazione a volte utile”.

“Andiamo bene”.

“Però, sì, anche in fisica esiste il baricentro”.

“Che ha qualcosa a che fare con la forza di gravità, mi pare”.

“E infatti in questi disegni abbiamo un solido pesante”.

“Io vedo un triangolo”.

“Non vedere un triangolo, ma un solido formato da tre masse uguali, poste nei vertici del triangolo”.

“E questo lo vediamo grazie a quei numeri 1 che ogni tanto compaiono?”.

“Esatto. Compaiono quando servono. All'inizio poniamo l'attenzione solo su due delle tre masse”.

“Quelle in basso”.

“Quelle in basso nella figura, sì. Possiamo pensare alla base del triangolo come a un'asta alle cui estremità sono fissate due masse”.

“Ok”.

“Ora, al posto di quelle due masse possiamo sostituire una massa doppia messa al centro del lato”.

“Perché al centro?”.

“Se vogliamo che quell'asta sia in equilibrio, la massa dovrà stare al centro. Se fosse spostata verso destra o verso sinistra sarebbe sbilanciata”.

“Come un'altalena?”.

“Esattamente. O come una bilancia antica, a due piattelli: il fulcro sta al centro e il braccio è in equilibrio se sul piattello di destra e su quello di sinistra ci sono gli stessi pesi”.

“Ok”.

“Nella terza figura, mettiamo in gioco anche il terzo vertice”.

“Vedo anche una nuova asta”.

“Sì, che collega il terzo vertice alla massa doppia che abbiamo usato prima”.

“E ora dobbiamo mettere in equilibrio questa nuova asta”.

“Esatto”.

“Dove va il fulcro? Non al centro, no?”.

“No: ricordi cosa diceva Archimede?”.

“Eureka?”.

“Anche. La leggenda racconta che pronunciò anche questa frase: datemi un punto d'appoggio e solleverò il mondo”.

“E cosa significa?”.

“Aveva scoperto il principio di funzionamento delle leve: se sposti il fulcro puoi sollevare grossi pesi facendo poca fatica”.

“Mh, e come?”.

“Il fulcro divide l'asta in due parti: l'asta sarà in equilibrio se il prodotto fra la distanza massa-fulcro e la massa è costante per entrambe le masse”.

“Eh?”.

“Se hai una massa uguale a 2 e una seconda massa uguale a 1, allora il fulcro divide l'asta in due parti che saranno una doppio dell'altra. La parte più corta sta dalla parte della massa maggiore, la parte più lunga dalla parte della massa minore”.

“Ah, ecco perché 1/3 e 2/3”.

“Esatto: l'asta viene divisa in tre parti, il fulcro ne tiene una da un lato e due dall'altro. In questo modo i prodotti massa-distanza sono costanti”.

“Vedo”.

“E quindi abbiamo trovato il baricentro, cioè il punto in cui possono essere concentrate le tre masse. E anche il punto che divide le mediane in due parti, una doppia dell'altra”.

“Molto bene. Ma questa è una vera dimostrazione?”.

“Perché no? La dimostrazione geometrica è diversa, usa le proprietà delle rette parallele e dei parallelogrammi, ma questa è più efficace, almeno dal punto di vista mnemonico”.

“Ok”.

“Poi, volendo, da qui si potrebbe partire per sviluppare strumenti notevoli per risolvere problemi difficili”.

“Aiuto”.

Giochi proiettivi — 2. Convergenze parallele

“C'è una cosa che non mi convince in quello strano esempio di geometria finita che mi hai fatto vedere l'altra volta”.

“Questo?”.

“Sì, questo. Non mi convince quell'arco: rovina la simmetria”.

“Avresti preferito una circonferenza?”.

“Sarebbe stato molto più bello e simmetrico, sì”.

“In effetti, la voce su Wikipedia relativa a questo modello, che si chiama Piano di Fano, mostra la figura che piace a te”.

“E perché tu l'hai disegnata così?”.

“Per non dare l'idea che la retta che contiene i punti D, E e F sia diversa dalle altre. Se disegnassi una circonferenza, questa retta sembrerebbe chiusa, mentre le altre no”.

“E non è così?”.

“No: le sette rette sono tutte fatte allo stesso modo, cioè sono tutte insiemi che contengono tre punti: se disegnassimo chiusa quella centrale, cosa che potremmo anche fare, dovremmo chiudere anche le altre sei, e il disegno risulterebbe inutilmente complicato”.

“Ah. Quindi la chiusura avrebbe un senso? Potrei percorrere le rette in cerchio, per così dire? Potrei camminare da A verso D, poi verso C, poi di nuovo verso A?”.

“Sì, nulla lo vieterebbe”.

“Che strana geometria”.

“Possiamo farla diventare una geometria un po' meno strana, forse, dando un ruolo speciale a una delle rette. Potremmo fare come si fa nei disegni in prospettiva: la retta all'orizzonte è una retta diversa dalle altre”.

“Nel senso che non esiste?”.

“Eh, quando si parla di esistenza in questo ambito i filosofi diventano matti. La retta all'orizzonte è una retta, è addirittura una delle prime rette che vengono disegnate quando si disegna a mano. Eppure è una retta fittizia, perché nella realtà (quale realtà, poi? non quella del disegno) non c'è”.

“Argh”.

“Per esempio, immaginiamo che la retta ad arco sia la retta all'orizzonte, quella che i Veri Matematici chiamano retta impropria”.

“Ok”.

“Togliamola dal disegno, allora. E togliamo quindi anche i tre punti da cui è composta: in effetti, la retta è l'insieme di quei tre punti”.

“Va bene, mi viene un disegno del genere:”.

“Benissimo. Ora hai anche delle rette parallele”.

“Cosa? Ma come? Dove?”.

“Per esempio le rette {A, C} e {B, G}”.

“Ah. Effettivamente non si incontrano”.

“Mentre prima si incontravano in D, un punto all'orizzonte”.

“Che strano”.

“Poi anche {A, G} e {B, C} sono parallele”.

“Vero: prima si incontravano in F. Infine {C, G} e {A, B} sono ancora parallele, e prima si incontravano in E”.

“Ottimo. Ora la figura è bella simmetrica come piace a te, anche se abbiamo perso qualcosa”.

“Che cosa?”.

“La dualità non funziona più: ora ci sono 6 rette, ma solo 4 punti”.

“Ah, già”.

“Questo è quello che si chiama piano affine, dove esiste ancora il parallelismo. Se completiamo ogni retta di un piano affine con un nuovo punto, un punto improprio, che è il punto di intersezione all'infinito di due rette parallele, otteniamo il piano proiettivo, quello da cui siamo partiti”.

“E i punti impropri che aggiungiamo costituiscono poi la retta impropria, giusto?”.

“Giustissimo.”.

“Bene, credo di aver capito, anche se questa faccenda della retta all'infinito mi pare ancora molto nebulosa”.

“Dopo ti faccio un altro esempio. Prima, però, una definizione: chiamiamo piano proiettivo di ordine n una geometria che soddisfa gli assiomi per un piano proiettivo finito e che ha almeno una retta con esattamente n + 1 punti distinti incidenti con essa, con n maggiore di 1”.

“Fammi capire: cos'è cambiato rispetto a prima?”.

“Prima abbiamo dato una definizione generica, adesso aggiungiamo il concetto di ordine. Insomma, cominciamo a contare le cose”.

“Mh. Quindi l'esempio che abbiamo visto, che contiene rette con tre punti, va bene, perché se n + 1 è uguale a 3 allora n è uguale a 2, e 2 è maggiore di 1”.

“Esatto. Quello che abbiamo visto è l'esempio di piano proiettivo più piccolo che possiamo fare”.

“Niente ordine 1?”.

“No, abbiamo scartato i casi degeneri l'altra volta, ricordi?”.

“Giusto. Esiste anche un esempio di piano proiettivo di ordine 3?”.

“Sì, ma te lo faccio vedere a partire dal piano affine di ordine 3. Prima di mostro alcune rette, poi ti faccio vedere come aggiungere la retta impropria”.

“Proviamo”.

“Cominciamo da qua”.

“Aiuto”.

“Allora, cominciamo dai punti: ce ne sono nove”.

“Benissimo”.

“Poi, per capire come sono fatte le rette, inizio col dirti che ogni retta contiene tre punti”.

“Ok”.

“Le rette facili sono quelle disegnate in nero: tre orizzontali, tre verticali e due in diagonale ”.

“Ok, una diagonale ascendente e una discendente”.

“Esatto. Ora, per capire come sono fatte le altre, ho usato dei colori. La retta rossa, per esempio, contiene i tre punti A, H e F”.

“Vedo: sono sempre tre punti. Però non mi piace quell'arco”.

“Capisco, credo che questo non sia il modo più naturale di disegnare questo piano. Dovremmo immaginarci tre diagonali ascendenti, e non una, così come tre diagonali discendenti”.

“E come facciamo?”.

“Possiamo farlo in due modi. Il primo è pensare che ci troviamo su una carta geografica”.

“In che senso?”.

“Dobbiamo pensare che se usciamo da destra, nella carta geografica, rientriamo da sinistra, e viceversa”.

“Ah”.

“Così, per esempio, se parti da H, scendi verso sinistra e incontri D, poi continui ancora a sinistra e incontri C”.

“Uh, vedo. Vale per tutti i punti: è come se le diagonali più corte andassero a capo dall'altra parte”.

“Esatto. L'altro modo è quello di mettere i nove punti sulla superficie laterale di un cilindro, in modo da non avere una colonna di destra, una colonna di centro e una colonna di sinistra, ma tre colonne in posizioni indistinguibili. In questo modo ci sono tre diagonali discendenti e tre diagonali ascendenti, senza dover andare a capo”.

“Uh, bello questo metodo”.

“Ho provato a fare un disegnino con le tre diagonali discendenti: le figure tridimensionali non sono sempre belle, ma forse si capisce qualcosa: le rette sono tutte uguali. Non ho fatto le altre rette per non complicare troppo la figura”.

“Ah, ecco, vedo. Molto bene!”.

“Ora direi di riprendere il modello sul piano, per semplicità di disegno. Hai visto che ci sono tante rette parallele: in tutto dodici”.

“Sì, che hanno direzioni diverse”.

“Bene: a ognuna di esse aggiungiamo un punto all'infinito”.

“E come?”.

“Le prolunghiamo, e le facciamo incontrare. Ci sono tre rette che vanno in direzione nord-sud, tre rette in direzione est-ovest, tre che vanno da sud-ovest a nord-est, e tre che vanno da nord-ovest a sud-est.”.

“Quindi le prolunghiamo e le incurviamo un pochino?”.

“Sì, così:”.

“Santo cielo”.

“Ho dovuto rinunciare a un po' di simmetrie: come vedi, ho spostato tutti gli archi colorati da una parte, per non intralciare i prolungamenti”.

“Ah, gulp, vedo. Ma c'è molta roba in più rispetto a prima”.

“Sì, ci sono dodici prolungamenti: tre per le rette orizzontali, tre per le rette verticali, tre per quelle ascendenti verso destra, tre per quelle discendenti verso destra”.

“E ognuno dei quattro gruppi si interseca in un punto rosso”.

“Esatto, e quindi abbiamo quattro nuovi punti”.

“Che, aggiunti ai precedenti nove punti, danno un totale di tredici punti”.

“Ok”.

“Poi ci sono le rette: ne avevamo dodici, e abbiamo aggiunto quella all'infinito, quella verde”.

“Totale: tredici”.

“Ed ecco ripristinata la dualità: tredici rette, tredici punti. Ogni retta contiene quattro punti, per ogni punto passano quattro rette”.

“Devo ammettere che questa dualità è elegante. Ma questo numero di rette e punti, è un caso che sia 13?”.

“Naturalmente no”.

“Naturalmente”.

Giochi proiettivi — 1. Geometrie

“Giochi proiettivi?”.

“Già”.

“Ma proprio giochi veri? O giochi che piacciono solo ai matematici?”.

“Giochi veri, di quelli che si comprano in negozio”.

“Ah. Proiettivi”.

“Proiettivi”.

“Nel senso geometrico del termine?”.

“Esatto. Avrai sentito certamente parlare di geometria proiettiva”.

“Sicuro”.

“Guarda che ne avevamo già parlato”.

“Ah, ecco, non ho ripassato, ehm”.

“Beh, non è che dobbiamo ripetere tutto: ci basta ricordare che cosa sia una geometria”.

“Una?”.

“Sì, una perché ne esistono tante, a seconda di quello che vuoi conservare e quello che può invece variare.”.

“Ah, ora che rileggo, mi viene in mente qualcosa: una geometria è lo studio delle proprietà di uno spazio che sono invarianti rispetto ad un gruppo di trasformazioni”.

“Sì. Tanto per fare un esempio, ricorderai che a scuola si potevano studiare le proprietà delle figure congruenti, oppure le proprietà delle figure simili. In un caso ti interessano le dimensioni delle figure, nell'altro solo le forme: tutto dipende da quello che vuoi analizzare”.

“Sì, sì, capisco. Ma per i giochi che geometria ci interessa?”.

“Quella proiettiva”.

“Capirai, la più complicata”.

“Per la precisione: la geometria proiettiva finita”.

“Finita? Capisco sempre di meno”.

“Facciamo un passo alla volta. Non abbiamo nemmeno bisogno di ripetere tutto il discorso fatto quando abbiamo parlato del programma di Erlangen: ci basta ripartire dai postulati di Euclide”.

“Ah, proprio dalle basi”.

“Sì, e ce ne bastano proprio pochi”.

“Sarà. Mai fidarsi dei Veri Matematici quando fanno le cose facili”.

“Capisco. Come al solito, le cose possono complicarsi molto in fretta, ma noi rimaniamo sul semplice. Prima di tutto, una teoria ha bisogno di alcuni termini primitivi”.

“Quelli che non si possono spiegare ulteriormente, vero?”.

“Esatto. Quelli la cui natura, se così si può dire, verrà spiegata dalle regole del gioco”.

“Stiamo già giocando?”.

“In un certo senso sì: la geometria, e in generale le teorie matematiche, sono come un gioco. Tu apri la scatola, trovi degli oggetti, e ti chiedi cosa siano. Poi apri il manuale, e leggi che quell'affarino di plastica che hai in mano è un carro armato, che soddisfa a certe regole, che può muoversi solo in un certo modo, che può attaccare solo in un certo momento e seguendo certe altre regole, che può essere ucciso. Ma naturalmente non è un vero carro armato”.

“Decisamente no”.

“Quindi io ti dirò che gli oggetti del nostro gioco si chiamano punti e rette, ma non ti dirò che cosa sono, perché non posso andare più a fondo. Posso però dirti quali sono le regole che essi devono rispettare”.

“Va bene; quindi punti e rette sono gli unici enti primitivi della geometria?”.

“C'è anche un terzo oggetto: il concetto di incidenza”.

“Che sarebbe?”.

“Sarebbe una relazione tra punti e rette. Dato che è un concetto primitivo, non posso spiegartelo ulteriormente, però comunque cercherò di dirti qualcosa per farti capire da dove nasce. Del resto, anche se non ti ho detto che cosa sia un punto, tu un'idea mentale te la sei fatta”.

“Certo, so bene cos'è un punto”.

“Permettimi di dubitare. Anzi, vedrai tra un po' che quello che chiameremo punto non sarà per niente un oggetto che assomiglia ai punti a cui siamo abituati. Le rette, poi, lo saranno ancora meno”.

“Non saranno dritte?”.

“Non si potrà nemmeno parlare del concetto di essere dritto. Del resto, essere dritto significa stare su una retta, quindi c'è poco da spiegare”.

“Andiamo bene”.

“Dunque, stavamo parlando del concetto di incidenza. Quando parliamo normalmente, diciamo che un punto appartiene a una retta, no?”.

“Esatto”.

“Oppure che una retta passa per un punto, o che contiene un punto”.

“Ancora esatto”.

“Quindi esiste una relazione tra una retta e un punto, se il punto sta sulla retta o se, viceversa, la retta passa per un punto”.

“Sì”.

“Questa relazione la chiamiamo incidenza. Invece di dire che un punto sta su una retta, diremo che un punto è incidente alla retta. E invece di dire che una retta contiene un punto, diremo che la retta è incidente al punto”.

“E perché questo linguaggio orripilante?”.

“Per poter usare un solo termine invece di due diversi. Ci piace la simmetria: dato che il concetto è lo stesso, usiamo la stessa parola”.

“È bruttissimo”.

“Concordo. Infatti nel linguaggio comune continueremo a usare i vecchi termini. Però è importante sapere che si può unificare il concetto, rendendolo simmetrico, anche nel linguaggio”.

“Non capisco l'importanza”.

“Perché non ricordi più il concetto di dualità. Ma ne riparleremo”.

“Meno male. Ora diciamo le regole?”.

“Prima una definizione, che ci permette di scrivere in modo leggermente più carino le regole”.

“Ok”.

“Diciamo che punti incidenti a una stessa retta si dicono collineari”.

“Va bene”.

“Ora, le regole, cioè i postulati di Euclide, formulati secondo il linguaggio che abbiamo deciso di usare. Per ora ti dico i primi due, poi vediamo gli altri. Eccoli qua:”.

P1. Per ogni coppia di punti distinti esiste un'unica retta incidente a entrambi i punti.
P2. Per ogni coppia di rette distinte esiste un unico punto incidente a entrambe le rette.

“Mi sembrano condivisibili, mi pare che siano i soliti, a parte quel brutto incidente”.

“Ora cerco di spiegarti la bellezza di questo modo di procedere. Prendi il primo postulato, e scambia punti con rette”.

“In che senso?”.

“Cancella punti e scrivi rette, cancella retta e scrivi punto”.

“Ah, ma diventano uguali. Certo, dobbiamo sistemare un apostrofo e il genere degli aggettivi”.

“Questo passamelo. O preferisci che invece delle parole usi le formule? Con le formule non ci sono più problemi di apostrofi, di plurali e singolari, di maschili e femminili”.

“Ok, ok, va benissimo così. Se faccio quella sostituzione, il primo postulato diventa uguale al secondo”.

“O, se fai la sostituzione nel secondo, è quello che diventa uguale al primo”.

“Esatto”.

“Quindi, a questo livello, le regole non fanno differenza tra punti e rette. Se due persone aprono la scatola del gioco e uno crede che le pedine rosse siano le rette e le blu i punti, e l'altro invece crede il contrario, fino a questo momento le regole non dicono chi abbia ragione. Se avessimo usato il verbo appartenere per i punti e contenere per le rette, allora avremmo fatto una differenza. Con il verbo incidere manteniamo una perfetta simmetria. Anzi, il termine usato per questo tipo di simmetria dai Veri Matematici è dualità”.

“Va bene, allora”.

“Ora, in un mondo perfetto sarebbe bellissimo fermarsi qui: due soli postulati, uno che si può confondere con l'altro, e basta”.

“E non possiamo farlo?”.

“Eh, no. Introduciamo un postulato che ci permetta di escludere casi degeneri, coi quali non vogliamo avere a che fare perché porterebbero a introdurre un sacco di eccezioni nei teoremi che poi scriveremo”.

“Casi degeneri? In che senso?”.

“Pensa a una scatola con una pedina sola, per esempio”.

“E che gioco è, un gioco con una pedina sola?”.

“Appunto”.

“E poi, sarà un punto o una retta?”.

“Potrebbe essere sia un punto che una retta: sono entrambi casi degeneri che non vogliamo. Ancora peggio: pensa a una scatola vuota”.

“Bella fregatura! Ma le regole non proibiscono situazioni di questo tipo?”.

“Sai che in questo caso entrano in gioco le meravigliose proprietà dell'insieme vuoto”.

“Oh no”.

“Eh sì. Una scatola vuota è compatibile, per esempio, con la regola che dice che due rette devono intersecarsi in un punto: dato che di rette non ce ne sono, è impossibile che la situazione contemplata dalla regola non si verifichi”.

“Vabbé, il delirio dei Veri Matematici con l'insieme vuoto è proverbiale. Escludiamo pure questi casi degeneri”.

“Benissimo, ecco qua:”.

P3. Esistono almeno quattro punti distinti a tre a tre non collineari.

“Uhm, fammi capire. Così escludiamo strutture con pochi punti: ne servono almeno 4”.

“Bene. Questi quattro non stanno tutti sulla stessa retta. Anzi, se ne prendi tre, come preferisci, nemmeno quei tre stanno sulla stessa retta”.

“Quindi posso immaginarmi una cosa del genere?”.

“Puoi certamente farlo, ma sappi che non è l'unico modo per immaginarsi questa situazione”.

“Va bene, anche se ancora non capisco”.

“Porta pazienza: capirai”.

“Ok. Ma l'introduzione di questo postulato non porta una asimmetria nella dualità che tanto ti piaceva?”.

“Ah, ottima domanda! No, non lo fa: prova a enunciare il postulato duale”.

“Oh, allora, scambiando rette con punti mi verrebbe da dire una cosa del genere:”.

P4. Esistono almeno 4 rette distinte che a tre a tre non incidono sullo stesso punto.

“Ottimo, hai anche usato il verbo incidere”.

“E non dovremmo aggiungere questo postulato, per mantenere la dualità?”.

“No, se prendi i quattro punti del postulato 3, e consideri tutte le rette che passano per due di quei punti, il tuo postulato 4 è automatico”.

“Ah, ma lo vedo anche dal disegno!”.

“Esatto”.

“Bene, e adesso?”.

“E adesso preparati a una sorpresa: questi postulati non definiscono solo la geometria alla quale siamo abituati, ma definiscono anche altri tipi strani di geometrie. Anzi, a dir la verità mi aspettavo un'obiezione”.

“Quale?”.

“Questi tre postulati non prevedono le rette parallele, che nella geometria a cui pensiamo sempre esistono”.

“Ah, hai ragione. Anzi, il postulato 2 le vieta proprio, le rette parallele!”.

“Esattamente. In questo tipo di geometria le rette parallele non esistono. Per questo viene chiamata geometria proiettiva”.

“È quella dei disegni in prospettiva?”.

“Esatto: nei disegni in prospettiva le rette parallele non esistono: quelle che nella realtà sono parallele, in prospettiva si intersecano sulla linea d'orizzonte”.

“Va bene. Qual è, invece, la sorpresa a cui mi devo preparare?”.

“Eccola qua: quanti punti sono necessari per lavorare con questa geometria?”.

“Beh, infiniti, no? Devo sempre poter disegnare le rette”.

“E chi ha detto che le rette sono composte da infiniti punti?”.

“Eh, se sono rette devono per forza… No, mi fermo subito, non succede niente per forza”.

“Bene”.

“I postulati non parlano mai di infiniti punti”.

“Bene”.

“E mi pare che da nessuna parte sia sottinteso il concetto di infinito. Nella geometria euclidea c'erano dei postulati apposta che ci permettevano di capire che una retta contiene infiniti punti”.

“Benissimo. Qua invece no: quindi è lecito che nella nostra scatola che contiene le pedine di questo gioco ci sia un numero finito di oggetti”.

“Che strano”.

“Ecco una configurazione di punti e rette che rispetta i postulati”.

“Cosa sto guardando? Una figura?”.

“No, l'universo di questa geometria. È composto da 7 punti: A, B, C, D, E , F, G”.

“Questi li vedo”.

“Poi ci sono delle rette. Tieni presente che, anche se sono disegnate come segmenti, in realtà non sono composte da infiniti punti. I segmenti ci servono solo per vedere meglio la struttura ma, tanto per fare un esempio, la retta che passa per A, E e B non contiene altri punti”.

“È una retta composta da soli tre punti?”.

“Esatto”.

“Che roba”.

“E quell'arco?”.

“È una retta anche lui”.

“Ma come? Non è drit… oh”.

“Già”.

“Non c'è scritto da nessuna parte che una retta è dritta”.

“Già. Inoltre, l'arco non esiste nemmeno, è solo un ausilio per raggruppare i punti”.

“Ah, va bene, che roba”.

“Avrei anche potuto descrivere gli oggetti senza l'ausilio di un disegno, ma sarebbe stato più brutto e meno comprensibile”.

“Come?”.

“Così: ti ho già fatto l'elenco dei punti, mi basta fare anche quello delle rette”.

Elenco delle rette:
{A, E, B}
{A, G, F}
{A, D, C}
{D, E, F}
{B, G, D}
{B, F, C}
{C, G, E}

“Tutto qua?”.

“Tutto qua. Puoi verificare che i tre postulati sono validi: se scegli due punti qualsiasi, c'è una sola retta che passa per entrambi. Se scegli due rette, queste si intersecano in un solo punto. Infine, esistono quattro punti a tre a tre non allineati, per esempio A, E, G, D”.

“Ed esistono anche quattro rette che non passano per uno stesso punto. Anzi, per ogni punto passano esattamente tre rette”.

“E allora sarà vera anche la proposizione duale: riesci a vederla?”.

“Dovrebbe essere: ogni retta contiene esattamente tre punti. Ed è vero!”.

“Benissimo”.

“Che strano, una geometria con sette punti e sette rette. Ma è un caso che il numero di punti e il numero di rette siano uguali?”.

“Hai già dimenticato la dualità?”.

“No ma… Ah! Se devo poter scambiare punti con rette, il numero dei punti deve essere uguale a quello delle rette, altrimenti non ce la faccio”.

“Proprio così”.

“E adesso?”.

“Adesso, facciamo qualche altro esempio, ragioniamo un po' su quello che succede, poi giochiamo”.

“Ottimo!”.

Nodi di carta

“Cos'è un nodo?”.

“Un nodo… un nodo è… un nodo è un nodo!”.

“Certo. Un Vero Matematico non sarebbe molto contento di questa definizione”.

“I Veri Matematici non sono mai contenti di nulla. Come lo definiscono un nodo, loro?”.

“Direbbero che un nodo è una curva semplice chiusa nello spazio”.

“Ah”.

“Ma se vai nel dettaglio, la definizione potrebbe risultare leggermente più incomprensibile”.

“Naturalmente”.

“Per esempio, se vai a vedere la voce sulla Wikipedia in italiano, trovi una frase che afferma che sarebbe sbagliato definire un nodo come l'immagine di una funzione continua dalla circonferenza nello spazio, perché così tutti i nodi risulterebbero equivalenti”.

“Interessante”.

“Se vai sulla analoga voce in inglese, invece, trovi scritto: a knot is an embedding of a circle in 3-dimensional Euclidean space, considered up to continuos deformations”.

“Eh? Ma è esattamente quello che la voce in italiano segnala come sbagliato”.

“Appunto”.

“Roba da matti”.

“Insomma, dato che non dobbiamo fare teoria dei nodi, a noi basta sapere che un nodo è una cosa di questo tipo. Questo si chiama nodo trifoglio”.

“Ok”.

“Mentre questo non è un nodo”.

“E perché no?”.

“Perché non è una curva chiusa. Un finto nodo come questo puoi sempre scioglierlo, mentre un nodo vero come quello della prima immagine non può essere sciolto, in modo da formare una circonferenza non annodata. Devi tagliarlo”.

“Ah, ecco. Ammesso che gli estremi non siano collegati in qualche modo, questo puoi scioglierlo, e farlo diventare un segmento”.

“Proprio così. Ricordi che abbiamo lavorato con una striscia di carta, un po' di tempo fa?”.

“Ricordo”.

“Ora proviamo a annodarla con un nodo semplice, ma non incolliamo gli estremi”.

“Insomma, proviamo a fare una cosa che tutte le persone appartenenti al mondo normale, eccetto quindi i Veri Matematici, chiamano nodo”.

“Esatto. Ecco una simulazione di nodo, con la quale puoi giocare”.



“Ah, vedo. Mi aspettavo qualcosa di curvo, mentre vedo dei segmenti”.

“Se tu prendi una vera striscia di carta e provi a annodarla, è vero che la incurvi. Ma a un certo punto puoi decidere di schiacciare tutta la carta su un piano, formando delle pieghe. La sostanza del nodo non cambia”.

“Ah, va bene. Vedo che posso cambiare dei parametri, ma non capisco quello che sto facendo”.

“Puoi cambiare lo spessore della carta, e puoi anche cambiare gli angoli secondo i quali pieghi la carta”.

“Ah, ecco, vedo che posso fare nodi magrolini e nodi più pieni”.

“Sì. Puoi pensare di annodare una striscia sottile lasciando spazio intorno alle anse del nodo, oppure puoi pensare di stringere il nodo più che puoi. In questa simulazione, invece di stringere il nodo allarghiamo la striscia di carta”.

“Capisco: è la stessa cosa. Come se guardassimo il nodo con uno zoom regolabile, in modo da tenere costante la dimensione del nodo”.

“Proprio così. Ora, una domanda: qual è la figura più simmetrica che puoi ottenere?”.

“Fammi provare… Il foglio di carta si piega tre volte, devo cercare di fare in modo che i tre angoli siano uguali, uhm”.

“Gioca un po' con i parametri che puoi regolare”.

“Ah, ecco! Se impongo che i due angoli siano di 36 gradi, salta fuori una bella figura simmetrica”.

“Bene, ora allarga più che puoi lo spessore del foglio di carta”.

“Ok… Bello! Se allargo al massimo si vede che riesco a riempire un pentagono”.

“Un pentagono regolare, esatto”.

“Perché?”.

“Gli angoli con i quali hai giocato, e che ora misurano 36 gradi, sono gli angoli secondo i quali è stata piegata la carta. Se osservi bene la figura, noterai che il lato della striscia, prima di essere piegato, è parallelo a un lato del pentagono; dopo la piega, è ancora parallelo a un altro lato”.

“Ah, vedo: la striscia è parallela a un lato, si piega su un secondo lato, adiacente al primo, e dopo la piega è parallela al lato adiacente al secondo”.

“E questa è proprio una caratteristica del pentagono: gli angoli interni di un pentagono regolare misurano 108 gradi, e l'angolo formato da due lati non consecutivi è proprio di 36 gradi”.

“Davvero?”.

“Guarda questa figura”.

“Ah, ok, vedo”.

“Quindi se tu prendi una striscia di carta e l'annodi, in modo da non lasciare spazi vuoti intorno alle pieghe, la figura che ottieni è un pentagono regolare”.

“E questo, però, non è un vero nodo matematico”.

“No, perché i capi del nodo sono liberi, e puoi sempre scioglierlo. Però, se i capi sono molto lunghi, puoi continuare a piegarli intorno al pentagono con regolarità”.

“Uhm, in che modo?”.

“Un capo parallelo a un lato del pentagono, dopo la piega, sarà parallelo a un altro lato del pentagono: puoi continuare a piegare seguendo i lati. Ogni piega segue un lato, e puoi continuare finché hai carta”.

“In modo da fare un blocchetto pentagonale”.

“Esatto. Questo è quello che fanno in Giappone, per esempio, quando piegano le cinture”.

“Ehh?”.

“Guarda qua”.

Strisce

“Oh, cos'è?”.

“Mi sto divertendo a piegare fogli di carta”.

“Ah, fai degli origami?”.

“Mh, no, niente di complicato. Mi stavo chiedendo come funziona la piegatura di una strisciolina di carta”.

“Non ti basta semplicemente piegarla, vero?”.

“Eh eh, sì, mi basterebbe anche. Però, vedi, se cominci a piegarla più volte saltano fuori delle belle forme, e allora uno vorrebbe provare a capire cosa c'è sotto”.

“Capirai”.

“Non è facile vedere le cose in tre dimensioni, e questo è un bell'esercizio”.

“Ah, vedo. Quindi, cos'hai scoperto?”.

“Beh, per prima cosa una striscia di carta è definita dai suoi due bordi”.

“E fin qua ci siamo”.

“Poi, vedi che per piegare la striscia si deve effettuare una rotazione intorno alla piega”.

“Sì. Io faccio però fatica a capire cosa si può fare e cosa non si può fare, quando si piega della carta”.

“Cioè?”.

“Il problema è che la carta non è rigida, ma non è nemmeno gomma. Quindi ci sono movimenti che sono permessi, e movimenti che invece non sono permessi”.

“Esatto, puoi piegarla ma non puoi allungarla o accorciarla. Puoi fare rotazioni, ma le lunghezze dei segmenti devono rimanere invariate”.

“Sì, la teoria è abbastanza semplice. Il difficile qua è vedere quello che succede. Per esempio, di quanto risulta inclinata la striscia dopo la piega?”.

“Ah, ottima domanda. Come faresti per rispondere?”.

“Eh, qui sta il punto. Io prenderei in mano una striscia vera e proverei”.

“Ottimo inizio: c'è chi si diverte a fare geometria senza figure, ma noi non siamo tra questi”.

“Meno male. Però, dopo aver giocato con la carta, non saprei andare avanti”.

“Bisognerebbe riuscire a passare dalla figura tridimensionale a una figura bidimensionale, così le cose diventerebbero molto più semplici”.

“Ah, certo. Però, ora che ci penso, se faccio una piega completa arrivo a una figura bidimensionale…”.

“Vai avanti”.

“Il foglio iniziale è piano, no? Poi lo piego, e non rimango più su un piano. Ma se la piega compie una rotazione di 180 gradi…”.

“Ottimo, concludi”.

“Se la piega consiste in una rotazione di 180 gradi, il risultato finale è ancora un piano. Schiaccio il foglio su sé stesso.”.

“Giusto”.

“Ora dovrei capire come risulta la figura finale, però”.

“Hai già capito molto: hai detto che ruoti di 180 gradi intorno a un asse”.

“Sì”.

“E questo è come dire che stai facendo una simmetria assiale”.

“Mh, suppongo di sì, sì. A dir la verità, non mi risulta facile nemmeno vedere come funziona una simmetria di una retta rispetto a un'altra retta”.

“Beh, questo è molto semplice: l'angolo formato tra le due rette non cambia”.

“Ah, già, vedo. La retta blu viene trasformata nella retta rossa, vero? I due angoli formati dalle due rette con l'asse di simmetria non cambiano”.

“Sì. Naturalmente puoi anche dire che è la retta rossa che viene trasformata nella retta blu”.

“Giusto, certo. Posso piegare il foglio da sopra a sotto o da sotto a sopra, non importa”.

“Ok. Ora ti mostro l'applicazione di questa semplice regola a una striscia di carta”.

“Oh, quanti colori”.

“Sì, potevo fare ricorso a una maggiore sobrietà. Però così si distinguono tutte le parti”.

“Ok, vedo la striscia verticale”.

“Esatto”.

“Che poi viene piegata lungo la linea tratteggiata. Riconosco anche gli angoli uguali come mi hai fatto vedere prima, sono quelli verdi”.

“Molto bene”.

“Poi ci sono altri angoli, però”.

“Sì, qui ho fatto un passo avanti. Se la piega fosse perpendicolare ai bordi della striscia, si avrebbe una figura poco interessante: la striscia si ripiegherebbe completamente su sé stessa, e tanti saluti allo studio degli angoli”.

“Ok”.

“Allora la domanda è: se la piega è inclinata, rispetto all'orizzontale, di un certo angolo…”.

“Quello evidenziato di rosso, giusto?”.

“Proprio quello. Se la piega è inclinata, rispetto all'orizzontale, dell'angolo colorato di rosso, di quanto risulta inclinata la striscia?”.

“Non è una risposta facile, mi pare”.

“Diventa facile se osservi una sola cosa: l'angolo rosso e l'angolo verde sono legati da una certa relazione”.

“Uhm. Vedo un triangolo che li contiene entrambi”.

“Esatto”.

“Ah! Un triangolo rettangolo! Quindi l'angolo rosso e quello verde sono complementari”.

“Giusto, e adesso tutti gli angoli segnati in figura dovrebbero essere evidenti”.

“Lo sono, sì. Hai tracciato, in grigio, la perpendicolare all'asse di simmetria, quindi ecco un altro angolo retto, ed ecco i due angoli complementari”.

“Ecco fatto, quindi”.

“Mi pare, allora, che l'angolo con cui la striscia viene deviata, per così dire, sia il doppio dell'angolo rosso”.

“Ed è così”.

“E adesso?”.

“Adesso facciamo un nodo”.

L'inverso del teorema di Pitagora

“L'inverso del teorema di Pitagora?”.

“Eh, sì”.

“Ma cosa significa inverso?”.

“Ti giro la domanda: cosa dice il teorema di Pitagora?”.

“Dice che il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti”.

“No”.

“Come no?”.

“No: prendi un triangolo equilatero di lato 1 e dimmi se è vero che 1 + 1 = 1”.

“Ma cosa c'entra un triangolo equilatero? Il triangolo deve essere… Ok, non l'ho detto”.

“Già”.

“Riprovo: il teorema di Pitagora dice che in un triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti”.

“Ottimo. Qual era l'errore, quindi?”.

“Avevo dimenticato di specificare il contesto in cui si applica il teorema”.

“Sì, avevi dimenticato l'ipotesi: il teorema di Pitagora vale se il triangolo è rettangolo”.

“E l'inverso, allora?”.

“L'inverso risponde a quest'altra domanda: è vero o no che il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti solo se il triangolo è rettangolo?”.

“Ovvio”.

“Mica tanto ovvio: prendi un triangolo, indica con a, b e c i suoi tre lati, sai che vale la relazione a² + b² = c². Puoi dire che il triangolo è rettangolo?”.

“Ma per forza, no?”.

“NO! NON ESISTONO DIMOSTRAZIONI PER FORZA!”.

“Ok, ok, mamma mia che brutto carattere”.

“Scusa eh, ma se tu sai che il verificarsi di qualcosa implica il verificarsi di qualcos'altro, puoi dire che automaticamente il verificarsi della seconda cosa implica il verificarsi della prima?”.

“Fino a pochi secondi fa avrei detto di sì, ma mi pare di capire che invece non sia così. Ho un po' paura a chiedere perché, però”.

“Prendi un numero divisibile per 4: puoi dire che è divisibile anche per 2?”.

“Certo”.

“Perché?”.

“Perché se contiene 4 contiene anche 2, dato che 4 è divisibile per 2”.

“Questa proprietà vale per tutti i numeri divisibili per 4?”.

“Certo”.

“Puoi dire il contrario? Puoi dire che ogni numero divisibile per 2 è divisibile anche per 4?”.

“Eh, no, non tutti. Se prendo 8 va bene, se prendo 6 no”.

“Quindi questo è un esempio di teorema che funziona in una sola direzione: il suo inverso non è un teorema”.

“Ah”.

“È vero che un quadrato ha quattro angoli retti?”.

“Certo”.

“È vero il contrario? Che se un quadrilatero ha quattro angoli retti allora è un quadrato?”.

“Eh, no, un rettangolo ha quattro angoli retti ma non è un quadrato”.

“Non è detto che lo sia, volendo essere precisi”.

“Può esserlo?”.

“Beh, sì. Se la definizione di rettangolo è quadrilatero con quattro angoli retti, allora esso potrebbe anche essere un quadrato. Ma non è vero che ogni rettangolo è un quadrato”.

“Va bene, ho capito”.

“Tornando al teorema di Pitagora: è vero che se in un triangolo il quadrato di un lato è equivalente alla somma dei quadrati degli altri due lati, allora quel triangolo è rettangolo”.

“A questo punto non so più quale sia la risposta. Direi di sì, ma non so perché”.

“La risposta è sì, anche se ormai il motivo per cui quella risposta è affermativa è sparito dai libri scolastici”.

“Perché?”.

“Non ne ho idea. Pigrizia? Poca voglia di spiegare? Chissà”.

“Ma è una dimostrazione difficile?”.

“No, non direi. Te la mostro, nella versione di Euclide. Cominciamo da un triangolo ABC per il quale vale la relazione AB² + AC² = BC². Eccolo qua”.

“Ok. Quindi non sappiamo se è rettangolo, e vogliamo dimostrarlo”.

“Esatto: vogliamo dimostrare che l'angolo in A è retto”.

“Va bene, cominciamo”.

“Dobbiamo fare una costruzione: costruiamo un segmento DA che forma un angolo retto con CA”.

“Quindi prolunghiamo AB? Ma non sappiamo se l'angolo A è retto oppure no”.

“Esatto, ottimo: non prolunghiamo, ma costruiamo noi un angolo che sia retto. Questo vuol dire che ancora non possiamo sapere se i tre punti D, A e B sono allineati oppure no”.

“Ho capito. Quanto deve essere lungo il segmento DA?”.

“Tanto quanto AB”.

“Perfetto, eccolo qua”.

“Poi congiungiamo D con C e formiamo un triangolo”.

“E, questa volta, sappiamo che è un triangolo rettangolo”.

“Proprio così, ecco la figura completa”.

“Ora che si fa?”.

“Scriviamo un po' di uguaglianze. La prima è questa, sei d'accordo? DA² = AB²”.

“Eh, beh, sì, se DA è uguale a AB lo saranno anche i loro quadrati”.

“Già. Ora aggiungiamo, a destra e a sinistra dell'uguale, la stessa quantità, cioè AC²”.

“Così? DA² + AC² = AB² + AC²”.

“Esatto. Ora guarda cosa c'è a sinistra dell'uguale”.

“C'è la somma dei quadrati di DA e AC… Ah! Il triangolo DAC è rettangolo, quindi per quello posso applicare il teorema di Pitagora, vero?”.

“Certo: questa dimostrazione si appoggia su quel teorema. Prima dimostri il teorema diretto, poi questo”.

“Ah. Ma si può?”.

“Certo, non stai facendo le cose in modo circolare: prima dimostri il teorema di Pitagora, senza usare questo teorema, poi dimostri questo usando quello che hai appena dimostrato”.

“Ok, mi piace. Quindi siamo arrivati al fatto che a sinistra dell'uguale si può applicare il teorema di Pitagora: lo facciamo?”.

“Sì, e quindi possiamo sostituire, al posto di DA² + AC², il quadrato dell'ipotenusa, cioè DC²”.

“A destra dell'uguale, però, non posso farlo, perché non so se il triangolo sia rettangolo oppure no”.

“No, ma non ti serve saperlo: per la parte di destra puoi usare direttamente l'ipotesi. Tu sai già quanto vale quella somma”.

“Ehi, ma è vero, è proprio l'ipotesi! So che AB² + AC² è uguale a BC²”.

“Certo, e quindi l'uguaglianza è diventata DC² = BC²”.

“Ma allora posso dire che DC e BC sono uguali”.

“Proprio così: quindi i due triangoli ABC e ACD hanno i tre lati ordinatamente congruenti”.

“E allora sono triangoli congruenti, no?”.

“Sì, è così, per il cosiddetto terzo criterio di congruenza dei triangoli. A questo punto, abbiamo concluso: se i due angoli DAC e CAB sono congruenti…”.

“…dato che DAC è retto, dovrà esserlo anche CAB!”.

“Ed ecco fatto”.

“Avevi ragione, non era difficile. Dicevi che sui libri di scuola non si trova più questa dimostrazione, ma perché? Non è difficile, mi sembra un peccato non metterla”.

“Anche a me”.

Un piccolo contributo riguardo l'argomento del giorno: la bicicletta con ruote quadrate

Primo quesito dell'esame di stato di liceo scientifico, anno scolastico 2016-2017, sessione ordinaria.

Il problema di Didone

Giunsero in questi luoghi, ov’or vedrai
Sorger la gran cittade e l’alta ròcca
De la nuova Cartago, che dal fatto
Birsa nomossi, per l’astuta merce
Che, per fondarla, fêr di tanto sito
Quanto cerchiar di bue potesse un tergo.

“Ma cos'è?”.

“L'Eneide, libro 1”.

“E, ehm, di cosa parla?”.

“Della fondazione di Cartagine. L'astuta Didone aveva avuto il permesso di occupare tanta terra quanta ne potesse contenere una pelle di bue. Lei allora prese la pelle di bue, la tagliò in tante striscioline, le collegò insieme, e circondò una zona di terra semicircolare, il cui lato rettilineo era la spiaggia. Sul quel terreno fece costruire Cartagine”.

“Brava questa Didone”.

“Eh sì. E naturalmente i matematici si sono posti un problema”.

“Capirai”.

“Poteva fare di meglio? Poteva circondare una zona di terreno ancora più ampia?”.

“Ovviamente”.

“Eh? Ma no, come?”.

“Le sarebbe bastato prendere un bue più grande. Non mi sembra un gran problema matematico”.

“Ah. Eh. No. Cioè, il problema dice: a parità di lunghezza della striscia fatta con la pelle di bue, si possono circondare zone più grandi?”.

“Ecco, adesso è un po' diverso. Beh, non ha scelto la forma migliore? La semicirconferenza non va bene? Doveva fare un rettangolo? Un quadrato? Una strana figura esistente solo nella mente dei Veri Matematici?”.

“La semicirconferenza va bene, in effetti”.

“E allora, qual è il problema?”.

“Come dimostri che quella scelta da Didone è davvero la superficie di area massima?”.

“Mi sembra ovvio”.

“Le dimostrazioni per ovvietà, però, non sono ammesse tra i matematici”.

“Uff. E quindi?”.

“E quindi bisogna saltare dai tempi di Didone fino al 1838, quando venne pubblicata la dimostrazione di Steiner relativa al problema isoperimetrico”.

“Isoperimetrico, certo”.

“Il problema, formulato in termini matematici, dice questo: tra tutte le figure aventi lo stesso perimetro, qual è quella di area massima? Da cui il termine isoperimetrico”.

“Ah, ok. E quindi nel 1838 è stato dimostrato che Didone aveva scelto la soluzione giusta?”.

“Sì, da Steiner. Con una dimostrazione che, però, era sbagliata”.

“Perfetto”.

“Non troppo però. Adesso te la racconto”.

“Vai. Una dimostrazione non troppo sbagliata. Mah”.

“Bisogna fare questa premessa: Didone aveva a disposizione la spiaggia, cioè un segmento rettilineo, che poteva usare in modo da risparmiare la sua preziosa pelle di bue. Se non puoi usare nessun tipo di segmento, la figura che massimizza l'area è la circonferenza”.

“Mi sembra altrettanto ovvio”.

“Perfetto, questa ovvietà viene dimostrata da Steiner”.

“Sbagliando”.

“Un pochino”.

“…”.

“Steiner afferma, come primo passo della sua dimostrazione, che la figura che risolve il problema isoperimetrico deve essere convessa”.

“Mi sembra ovvio, ma capisco che dirlo non fa fare nessun passo avanti al Vero Matematico Dimostratore”.

“No, certo. Ma immagina una qualsiasi figura che non sia convessa. Ti disegno un poligono, ma va bene anche una figura con lati curvilinei”.

“Ok, quindi?”.

“Mi basta riflettere la parte concava all'esterno, fare diventare la figura convessa, e aumentare l'area senza toccare il perimetro. Guarda”.

“Ah, vedo. Ok, la figura deve essere convessa”.

“Secondo passo: prendo la figura, e la taglio in modo da formare due figure aventi lo stesso perimetro”.

“La taglio a metà”.

“Eh, ma bisogna stare attenti: non la taglio in due parti aventi la stessa area, ma in due parti aventi lo stesso perimetro. Se la figura è tutta deformata, non è detto che sia la stessa cosa”.

“E quindi?”.

“E quindi se le due parti non hanno la stessa area, buttiamo via la parte con area minore e la sostituiamo con una copia di quella con area maggiore: non abbiamo cambiato il perimetro, ma abbiamo aumentato l'area”.

“Mmmh, e questo cosa ci dice?”.

“Che possiamo lavorare solo su mezza figura, facendo come Didone. L'altra metà la otteniamo per simmetria”.

“Mettiamo una spiaggia anche noi, insomma”.

“Esatto. Adesso, prendiamo la nostra mezza figura, e costruiamo un triangolo al suo interno”.

“Ok, che ci facciamo?”.

“Ci domandiamo se è rettangolo”.

“Boh, e chi lo sa? Potrebbe esserlo o non esserlo”.

“Esatto. Se lo fosse, per ogni scelta del punto sulla curva blu, potremmo dire qualcosa”.

“Se ben ricordo, i triangoli rettangoli sono inscritti nelle semicirconferenze”.

“Già. Se, comunque noi scegliamo la posizione del punto sulla curva blu, il triangolo che disegniamo è rettangolo, allora la curva è una semicirconferenza”.

“E, in questo caso, abbiamo Cartagine. Se, invece, il triangolo non fosse rettangolo, come nella figura?”.

“Se il triangolo non fosse rettangolo, noi potremmo modificare la figura, spostando il punto, in modo da ottenere un triangolo rettangolo. Facendo questo non modifichiamo il perimetro della curva blu, ma soltanto la sua forma”.

“In che senso non modifichiamo il perimetro?”.

“Immagina che il triangolo dentro alla figura sia un buco, e che esistano solo le due parti delimitate dalla curva blu, come se fossero due lunette incollate sui lati del triangolo”.

“Ok”.

“Ora modifichiamo l'angolo del triangolo, lasciando le lunette attaccate ai lati, fino a farlo diventare retto. Non cambiamo nessuna misura”.

“Va bene, quindi? Che succede?”.

“Succede che l'area delle lunette non è stata toccata, mentre l'area del triangolo si è modificata. Ti disegno solo il triangolo (perché non sono capace di spostare anche le lunette, ehm)”.

“Vedo, ma non capisco”.

“Devi capire se l'area del triangolo è cambiata”.

“Sicuramente. Cioè, boh, non so, a dir la verità. Abbiamo cambiato solo un angolo, alla fine”.

“Esatto. Ricordi come si calcola l'area di un triangolo…”.

“Base per altezza diviso due!”.

“…di cui conosci due lati, non la base e l'altezza?”.

“Ehm”.

“Ecco qua: conosci i lati b e c, e l'angolo compreso tra essi”.

“Ah, posso trovare l'altezza moltiplicando b per il seno dell'angolo”.

“E quale angolo ha il seno maggiore?”.

“Quello retto, ho capito. Costruendo un triangolo rettangolo massimizziamo l'area, quindi se il triangolo che avevamo inizialmente non era rettangolo, possiamo modificare la curva in modo tale che il perimetro rimanga fisso e aumenti l'area”.

“Conclusione, dice Steiner, la figura che massimizza l'area è quella per la quale ogni triangolo che possiamo costruire al suo interno è rettangolo”.

“Cioè la semicirconferenza. Fine della dimostrazione”.

“Fine della dimostrazione sbagliata”.

“Ma come?”.

“Eh, oh”.

Una delle (tante) proprietà della sezione aurea

Una versione animata (e senza parole) del teorema di Pitagora

Penso che ci sia poco da dire, se non: siamo sicuri che la figura costruita su c sia proprio un quadrato? (Sì, perché gli angoli acuti dei triangoli rettangoli sono complementari)

Ma lo sapete perché usate i quaderni a quadretti?

“E quelli che hanno i fogli a righe? Eh? Eh? Già coi quadretti non son capaci di fare un disegno decente, figuriamoci con le righe!”.

“Calma”.

“Santo cielo!”.

“Rilassati, dai”.

“E il righello? Almeno un righello, no? Cosa ci vuole a usare un righello?”.

“Dai, su. Cosa succede?”.

“Eh, succede che ogni volta che vedi uno studente disegnare come se i quadretti non esistessero, ti senti un po' morire dentro”.

“Eh, via”.

“Non sanno fare un angolo retto nemmeno coi quadretti, ti dico! Ma non dico angoli retti che non seguono la griglia, eh, dico proprio angoli retti che usano gli angoli già disegnati”.

“Ehm, angoli retti che non seguono la griglia? Si può?”.

“CERTO CHE SI PUÒ, NON TI CI METTERE ANCHE TU EH?”.

“Ah, ma dai. Beh, usando le diagonali, certo, ci si riesce”.

“Non solo, puoi fare un po' quello che vuoi. Dai, ti faccio vedere qualche disegnino: guarda come è facile costruire dei quadrati”.

“Ah, ma guarda. E si possono fare anche altri poligoni?”.

“Beh, di poligoni ne fai finché vuoi. Se invece intendi poligoni regolari, c'è una bella dimostrazione senza parole che risponde alla tua domanda”.

“E qual è questa risposta?”.

“Te la lascio trovare guardando questa figura”.

“Bella, eh, ma non capisco cosa dimostri”.

“C'è un pentagono…”.

“E fin qui ci siamo”.

“Supponiamo che i suoi vertici stiano su una griglia quadrettata”.

“Ah, supponiamolo pure, ma se la disegnavi era meglio: io non ci riesco”.

“Certo, ma tra un attimo scoprirai perché non l'ho disegnata”.

“Va beh. Quindi?”.

“Sì. Dopo aver disegnato il pentagono iniziale, ho fatto ruotare ogni suo lato di 90 gradi in senso antiorario, intorno a uno dei due vertici”.

“Ah, ecco”.

“Ora, sarai d'accordo con me quando dico che se ruoto una griglia quadrata di 90 gradi, ottengo nuovamente la stessa griglia quadrata”.

“Senza dubbio, sì, sono d'accordo”.

“Quindi, se i vertici del pentagono grande stavano su una griglia quadrata, ci stanno anche i vertici che sono stati spostati dalle rotazioni”.

“Uhm, ma non hai mica applicato la stessa rotazione: il centro è stato spostato ogni volta”.

“Certo, ma quello che importa è che se ruoti di 90 gradi intorno a un punto della griglia, finisci sempre su un punto della griglia”.

“Ah, giusto”.

“Quindi i vertici ruotati, che sono vertici di un altro pentagono, stanno sempre sulla nostra griglia quadrettata”.

“Vero”.

“E allora vai avanti così, ripeti il procedimento. Prima o poi otterrai un pentagono più piccolo di un quadratino della tua griglia”.

“Mi sembra impossibile”.

“Lo è”.

“Ah, ecco. Quindi non si può fare un pentagono su una griglia quadrata: molto bene. È una proprietà specifica dei pentagoni?”.

“No, ti mostro qualche altra figura”.

“Ah, ma guarda. E funziona sempre?”.

“Beh, prova a pensarci un po'. Col quadrato non funziona, ad esempio”.

“E vabbé. Con gli altri poligoni?”.

“Qui hai visto pentagono, esagono e ettagono. Se aumenti il numero di lati, le figure non cambiano di molto: per essere più precisi, se ruoti i lati di 90 gradi e ricongiungi i vertici, ottieni un poligono più piccolo. Questo succede perché i punti, dopo la rotazione, finiscono all'interno del poligono iniziale”.

“Ah, ecco perché col quadrato non funziona: quando ruoti i lati riottieni la stessa figura”.

“Esattamente: i lati del quadrato già formano angoli di 90 gradi, quindi ruotandoli non cambia nulla. Il pentagono, invece, ha angoli interni maggiori di 90 gradi, e con la rotazione i lati finiscono al suo interno. Stessa cosa per l'esagono, l'ettagono, eccetera”.

“Interessante. Manca il triangolo, mi pare”.

“Manca il triangolo. E se ruoti i lati di un triangolo equilatero ottieni una figura più grande, non più piccola”.

“Oh. E allora come si fa?”.

“Beh, se fosse possibile mettere un triangolo equilatero su una griglia quadrata, ci si potrebbe mettere anche un esagono”.

“E perché?”.

“Eh, perché con sei triangoli equilateri fai un esagono”.

“Ah, giusto. E siccome l'esagono non si può disegnare, non si può disegnare nemmeno il triangolo”.

“Proprio così: se fosse possibile disegnare il triangolo, si potrebbe immediatamente disegnare l'esagono, ma siccome è impossibile disegnare l'esagono, allora è impossibile anche disegnare il triangolo”.

“Ottimo”.

“Ed ecco quindi il teorema: non esistono poligoni regolari non degeneri aventi i vertici su una griglia regolare, eccezion fatta per il quadrato”.

[Grazie a Joel David Hamkins]

Gli orologi di Fourier — 1. Homer Simpson destrutturato

“Guarda che bello!”.

“Ma cos'è?”.

“Un orologio…”.

“…con le lancette che vanno al contrario”.

“Eh, vabbé, è un orologio matematico. L'importante è che abbia almeno due lancette che si muovono a velocità diversa”.

“Almeno? Quante lancette vuoi?”.

“Un numero qualsiasi, basta che ruotino a velocità diverse”.

“Un orologio complicato”.

“Oh, sì, e lo complichiamo ulteriormente. Immagina di sommare, in un certo senso, le lancette”.

“E come si fa?”.

“Come se tu dovessi sommare dei vettori. In realtà quelle che tu chiami lancette dell'orologio sono vettori rotanti”.

“Ah. E come li sommo? Con la regola del parallelogramma?”.

“Quello è un modo, altrimenti potresti sommarli mettendoli in sequenza, la coda del secondo vettore parte dalla punta del primo. Quello che i fisici chiamano metodo punta-coda”.

“Vediamo: se li sommo con la regola del parallelogramma, otterrei una figura del genere”.



“Molto bene”.

“Non saprei come fare una figura in movimento col metodo punta coda, però”.

“Ecco qua:”.



“Ahh, ma è bellissimo! Epiciclo e deferente, vero?”.

“Esatto”.

“E adesso?”.

“E adesso sporchiamo un po' la figura: vediamo che traccia lascia la somma delle due lancette”.



“Molto bella”.

“E immagina i disegni che si possono fare con tre lancette, o quattro, o molte di più”.

“Chissà che complicazioni”.

“Guarda qua:”.



“!”.

“Bello, eh?”.

“Meraviglioso, ma come hanno fatto?”.

“Con una tecnica scoperta da Fourier”.

“E come funziona? Non saranno andati per tentativi, no?”.

“Eh, no, hanno preso l'immagine che volevano ottenere e hanno fatto andare le lancette al contrario”.

Il primo teorema di Euclide senza parole (e perfino animato)

(Il prossimo lo faccio con le pause, ora che ho imparato come si fa)

Dopo quanto spazio Achille riesce a raggiungere la signorina Tartaruga?

Ovvero: a quanto converge una serie geometrica convergente? Ecco una dimostrazione geometrica senza parole, che usa la similitudine dei triangoli.

Il determinante di una matrice, che rimane sempre un concetto misterioso

Tempo fa avevo scritto del determinante visto come volume orientato, e di come la sua definizione fosse necessariamente complicata (cioè: se vuoi una formula che funzioni in un certo modo, con determinate proprietà, allora deve essere fatta così).

Possiamo affrontare il problema anche in un altro modo: invece di elencare le proprietà e vedere come va a finire, facciamo il conto una volta per tutte. Lo facciamo in un caso particolare, quello bidimensionale, che riusciamo a visualizzare bene, perché spesso un disegnino spiega più di mille parole (se non sarà una dimostrazione generale da Veri Matematici, pazienza).

Quindi: cosa vogliamo fare? Vogliamo calcolare l'area di un parallelogramma conoscendo i due vettori che lo generano.

Ecco, questa immagine è una dimostrazione senza parole (quasi, via) del fatto che il determinante di una matrice quadrata rappresenta l'area di un parallelogramma generato dai due vettori (a,b) e (c,d), che nel disegno sono scritti in verticale così come si fa di solito in algebra lineare/geometria.

Ecco la spiegazione:

• Il rettangolo blu ha il lato orizzontale lungo a e quello verticale lungo d, quindi la sua area vale ad.
• Trasporto il triangolo rettangolo avente cateti a e b (quello con il tratteggio arancione) in alto.
• Trasporto il triangolo rettangolo avente cateti c e d (quello con il tratteggio viola) a destra.
• Osservo che in questo modo copro tutto il parallelogramma e anche qualcosa in più, e più precisamente il rettangolino in alto a destra, di dimensioni c e b, e quindi di area bc.
• Concludo quindi che l'area del parallelogramma si ottiene sottraendo l'area del rettangolino bc dall'area del rettangolone ad, cioè ad − bc.
• (Noto che devo sottrarre tutto il rettangolino bc e non solo la parte esterna al parallelogramma, perché la parte interna viene contata due volte (e infatti presenta un doppio tratteggio), mentre devo contarla una volta sola)
• Concludo che va tutto bene, quindi l'area del parallelogramma è proprio uguale al determinante della matrice.

Questo disegnino serve anche per capire perché funziona la misteriosa regola di Cramer per risolvere i sistemi lineari, ma questa è un'altra storia.

P.S. Questo è il millesimo post di questo blog. Incredibile.

Allora, questi angoli retti sono congruenti o no?

“Ma allora com'era la soluzione del paradosso degli angoli retti diversi?”.

“Hai provato a studiare il problema?”.

“Eh, sì, però non ho mica capito quale fosse l'errore: i due triangoli coi lati rosso, verde e viola sono effettivamente congruenti”.

“E questo è giusto”.

“Ma allora? Non è possibile!”.

“L'errore, questa volta, sta nella figura”.

“Ma come? La figura è corretta, non capisco”.

“La figura è sbagliata. Tu hai guardato quella che ho fatto io e non hai provato a costruirtela in autonomia, vero?”.

“Mah, a dir la verità ho provato a fare qualche scarabocchio, però non ho ottenuto nessun risultato. In fondo, che senso ha rifare una figura che ho già davanti?”.

“Se la figura è fatta bene potrei darti ragione, e però in questo caso non era fatta bene. Prova a farla utilizzando qualche strumento un po' preciso, senza pensare alla figura che già hai davanti”.

“Boh, proviamo pure”.

“Ti descrivo la procedura, poi tu esegui le varie operazioni, in questo modo non ti fai ingannare dalla figura che hai in mente”.

“OK”.

“Allora, disegna il rettangolo ABCD”.

“Fatto”.

“Ruota il segmento AB intorno al punto A, in senso orario, di un angolo scelto da te, a piacere. Il segmento ruotato lo puoi chiamare AE”.

“Bene”.

“Congiungi C con E, poi traccia gli assi dei due segmenti DA e CE. Chiama F il loro punto di intersezione”.

“Fatto. Oh”.




“Capisci, adesso?”.

“Capisco, i triangoli sono congruenti ma non sono disegnati come pensavo io. Ma forse se ruoto un po' di meno il primo segmento…”.

“Prova pure, questa non è un'immagine, puoi trascinare il punto E dove vuoi”.

“Uh. Ci deve essere una morale, in questa storia”.

“Già. Non fidarti dei disegni fatti dagli altri”.

“Pensavo a qualcosa un po' più zen”.

“Non fidarti, pensa”.

“OK”.

Non tutti gli angoli retti sono congruenti

A colori uguali corrispondono oggetti uguali. Dunque un angolo maggiore di un angolo retto è congruente a un angolo retto. Ehm.

---

Edit: siccome dal disegno non si capisce la costruzione, la esplicito qua, anche se non ho lettere sui vertici della figura.

Dato un rettangolo (quello coi lati blu e rossi in alto), ruotare di un certo angolo uno dei suoi lati (quello rosso in alto a destra). Costruire l'asse del lato lungo del rettangolo e l'asse del segmento arancione: si formano due triangoli isosceli (quello coi lati viola e quello coi lati verdi).

I due triangoli coi lati rosso, viola e verde risultano così congruenti.

Il determinante di una matrice, questo sconosciuto (per non parlare dei parallelotopi)

Qualcuno ricorderà, dalle scuole superiori, di avere già sentito nominare la parola determinante. Magari legata a un magico metodo per risolvere i sistemi di equazioni, il metodo di Cramer (che, tra parentesi, non si scrive con la K). Un metodo che aveva a che fare con le matrici, che sono poi griglie di punti — per la precisione, le matrici di cui si può calcolare il determinante sono griglie quadrate di punti.

Chi, all'università, studia matematica, o fisica, o qualche ingegneria, probabilmente incontra le matrici per la prima volta nel corso di geometria, l'unica materia che si studia senza fare nemmeno una figura (è così, sembra assurdo ma è così). La definizione di determinante di una matrice è del tutto incomprensibile: provo a scriverla in italiano.

Il determinante di una matrice quadrata n×n è dato dalla somma, fatta su tutte le permutazioni di n elementi, dei prodotti tra il segno della permutazione considerata e gli elementi di ogni riga (o di ogni colonna) riordinati secondo la permutazione stessa.

In formule:

La prima domanda che mi sono fatto io quando ho visto questa definizione è stata: ma come hanno fatto a pensarci? Quale mente malata può produrre una roba del genere? Nessuno te lo spiega, naturalmente, e tu rimani lì a bocca aperta in balia di sentimenti contrastanti: ammirazione per chi ha potuto pensare a una cosa del genere (che funziona, eh, non è scritta a caso) e odio per chi ha potuto pensare a una cosa del genere (che funziona, ma come è possibile che funzioni, santo cielo?).

Prima di provare a dare una spiegazione, ecco una citazione di un famoso matematico, Arnold, uno che faceva disegnini per ogni cosa (disegnava anche gattini) (per spiegare la matematica):

The determinant of a matrix is an (oriented) volume of the parallelepiped whose edges are its columns. If the students are told this secret (which is carefully hidden in the purified algebraic education), then the whole theory of determinants becomes a clear chapter of the theory of poly-linear forms. If determinants are defined otherwise, then any sensible person will forever hate all the determinants, Jacobians and the implicit function theorem.

Ecco. Visto cosa dice sul segreto indicibile riguardante il determinante?

Bene, proviamo allora a capire la definizione geometrica, quella con i disegnini. Partiamo da un parallelogramma:



Potete giocare un po' con l'applet trascinando le punte dei vettori: si vede bene che l'area dipende da quanto sono lunghi i vettori e dall'angolo compreso tra essi (se l'angolo diventa molto piccolo anche l'area diventa piccola). Se i due vettori sono sovrapposti (collineari, come dicono i Veri Matematici), l'area diventa nulla, e in effetti la figura non è più bidimensionale, ma è un segmento.

La stessa cosa vale in tre dimensioni e, se siete capaci di astrarre e diventare Veri Geometri, anche in un numero maggiore di dimensioni.



Il volume diventa uguale a zero quando almeno due dei tre vettori diventano collineari (se ci provate con la figurina qua sopra non è detto che ci riusciate, perché spostare con il mouse una proiezione bidimensionale di un oggetto tridimensionale non è facile. Insomma, il software fa quello che può (e che vuole)).

Ora, quello che vogliamo fare è definire un Coso Matematico che ci permetta di calcolare volumi di oggetti definiti come quelli qui sopra (cioè se parallelogrammi, con due vettori; se parallelepipedi, con tre vettori; se n-parallelotopi (pare che si chiamino così), con n vettori). Come fare?

Prima di tutto, la notazione: immaginiamo che i vettori partano tutti dall'origine, e quindi per definirli ci bastano le coordinate della loro punta. Due coordinate se siamo sul piano, tre coordinate se siamo nello spazio, n coordinate se siamo in spazi di dimensione n. Ecco, queste coordinate le mettiamo in colonna, formando una matrice (se decidessimo di metterle in riga non cambierebbe nulla, ma per fissare le idee pensiamo alle coordinate dei punti scritte in colonna).

Prima regola: un (iper)cubo di lato 1 deve avere area 1. In 2 dimensioni il cubo si chiama quadrato, definito dai vettori aventi estremi in (1,0) e (0,1), e quindi vogliamo definire il determinante in modo che dia come risultato 1 se applicato alla matrice avente come colonne (1,0) e (0,1). Insomma, in formule:

Questo deve valere in generale: in tre dimensioni, ad esempio, avremmo una matrice con tre righe e tre colonne così fatte: (1,0,0), (0,1,0), (0,0,1).

Insomma, abbiamo la

Regola 1: il determinante di una matrice avente 1 sulla diagonale che va dall'alto a sinistra al basso a destra e 0 in tutte le altre caselle deve valere 1. E fin qua ci siamo, andiamo avanti.

D'ora in poi indico con A₁, A₂, …, A_n le colonne della matrice (cioè le coordinate delle punte dei vettori).

Poco sopra abbiamo detto che se due vettori sono uguali allora il determinante deve dare zero. Quindi ecco la

Regola 2: det(A₁, …, A_i, …, A_j, …, A_n) = 0 se A_i = A_j per qualche coppia di valori i, j con i diverso da j.

Andiamo avanti: se moltiplichiamo un lato del parallelepipedo per un fattore λ (ai matematici che giocano con le matrici piace molto la lambda, chissà perché), allora il volume deve essere moltiplicato anch'esso per lo stesso valore. Quindi ecco la

Regola 3: det(λA₁, …, A_n) = λdet(A₁, …, A_n) — e questo deve valere per tutte le colonne della matrice, non solo per la prima.

Ora arriva una specie di proprietà distributiva. Cerchiamo di capirla prima con una figura (bidimensionale, così la vediamo meglio, eh):



Anche qua potete spostare le punte dei vettori. L'idea è questa: la somma delle aree dei due parallelogrammi azzurri è uguale a quella di quello rosso (i due triangoli che si formano sopra e sotto sono congruenti, in sostanza)(non fate commenti sui colori). Da qui deduciamo la

Regola 4: det(A₁ + B₁, …, A_n) = det(A₁, …, A_n) + det(B₁, …, A_n), e questo deve valere per tutte le colonne, non solo per la prima.

Ebbene, queste quattro regole ci permettono di definire il determinante e di arrivare alla Formulaccia Incomprensibile scritta lassù, basta fare un po' di giochini. Per esempio:

det(A₁ + A₂, A₁ + A₂, …, A_n) deve essere uguale a 0 per la regola 2 (ci sono due colonne uguali), ma se applichiamo per tre volte di seguito la regola 4 abbiamo che

det(A₁ + A₂, A₁ + A₂, …, A_n) =
= det(A₁, A₁ + A₂, …, A_n) + det(A₂, A₁ + A₂, …, A_n)
= det(A₁, A₁, …, A_n) + det(A₁, A₂, …, A_n) + det(A₂, A₁, …, A_n) + det(A₂, A₂, …, A_n)
= 0 + det(A₁, A₂, …, A_n) + det(A₂, A₁, …, A_n) + 0,

da cui ricaviamo che det(A₁, A₂, …, A_n) + det(A₂, A₁, …, A_n) = 0. Ed ecco la

Proprietà 1: scambiando di posto due colonne si inverte il segno del determinante (qui sono state scambiate le prime due, ma potete tranquillamente scambiare quelle che volete). E cambiare l'ordine di due vettori significa cambiare l'orientazione, ecco perché il determinante è il volume orientato del parallelepipedo. Insomma, diamo un significato anche al segno negativo.

Queste regole definiscono il determinante in modo non ambiguo, cioè lo caratterizzano. Vediamo per esempio come si fa per calcolare

Con la notazione usata qui (più comoda per un blog che usa l'html e non il LaTeX), i calcoli sono questi:

A = det((a,c), (b,d)) = det( a(1,0) + c(0,1), b(1,0) + d(0,1))

(applicando la regola 4:)
= det(a(1,0), b(1,0)) + det(a(1,0), d(0,1)) + det(c(0,1), b(1,0)) + det(c(0,1), d(0,1))

(applicando la regola 3;)
= ab[det((1,0), (1,0))] + ad[det((1,0), (0,1)] + bc[det((0,1), (1,0)] + cd[det((0,1), (0,1))]

(applicando la regola 2:)
= ab0 + ad[det((1,0), (0,1)] + bc[det((0,1), (1,0)] + cd0

(applicando la proprietà 1:)
= ad[det((1,0), (0,1)] − bc[det((1,0), (0,1)]
= (ad − bc)[det((1,0),(0,1)]

(applicando la regola 1:)
= ad − bc.

Ecco qua. Come si diceva a scuola: diagonale principale meno diagonale secondaria.

Se si applicano le stesse regole a matrici di ordine superiore ecco che salta fuori la somma fatta sulle permutazioni degli indici di cui si parlava all'inizio. Ora, almeno, c'è un perché che dà un'idea del motivo per cui la definizione sia fatta in quel modo.

Questo non è il percorso storico che ha portato alla definizione di determinante, e si può fare tanta matematica senza avere presente questo aspetto geometrico. Conoscerlo, però, secondo me è meglio.

---

Credits a Quora, che ogni tanto ha cose interessanti.