Facciamo un esempio. Prendiamo questa proiettività, dalle equazioni molto semplici:
Dobbiamo interpretare le equazioni in questo modo: noi abbiamo le coordinate (omogenee) di un punto (x,y,z), le inseriamo nelle formule e otteniamo le coordinate del punto trasformato (x',y',z').
Ora prendiamo questi quattro punti: A(-1,1,1), B(1,1,1), C(1,3,1) e D(-1,3,1), e li trasformiamo. Utilizzando le formule della proiettività, otteniamo A'(-1,-1,1), B'(1,-1,1), e fin qua è facile. Quando andiamo a fare i conti per C', risulta (1,-1,3): se ci ricordiamo che le coordinate sono omogenee, e quindi possiamo moltiplicare o dividere ogni termine per una costante arbitraria, possiamo scrivere che C' ha coordinate (1/3,-1/3,1), così lo possiamo rappresentare meglio. Analogamente per D' otteniamo (-1/3,-1/3,1).
Ecco un disegno:
Si capisce come agisce la trasformazione? Prende ciò che si trova al di sopra dell'asse x e lo rappresenta in prospettiva di sotto: in questo caso l'asse x diventa la linea d'orizzonte; le rette parallele BC e AD convergono in un punto. In pratica questa proiettività prende la retta impropria e la sposta al posto dell'asse x.
Ecco un altro esempio:
La figura ABCD è un rettangolo, le cui coordinate sono le seguenti: A(0,1), B(1,3), C(-3,5), D(-4,3). Se volete fare i conti, i punti trasformati sono A'(0,-1), B'(1/3,-1/3), C'(-3/5,-1/5), D'(-4/3,-1/3). Il rettangolo ha i lati opposti paralleli secondo due direzioni diverse, quindi AB e DC si incontrano nello stesso punto improprio, mentre BC e AD si incontrano in un punto improprio diverso (sono quelli che, in disegno tecnico, si chiamano punti di fuga): ecco un ingrandimento della figura in prospettiva.
Bene, trasformare i punti è facile. Ora vorremmo trasformare delle curve. È altrettanto facile purché capiamo una cosa: se la curva ha equazione f(x,y)=0, noi non possiamo prendere i suoi infiniti punti e trasformarli uno per uno, e allora giriamo il problema: prendiamo le equazioni della trasformazione geometrica e le inseriamo nella curva. Occorre quindi un passaggio preliminare, molto semplice: dobbiamo ricavare le coordinate x,y,z in funzione di x',y',z'.
Questa è quindi la trasformazione da usare per trasformare delle curve:
Trasformare alcune coniche sarà molto simpatico.
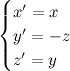



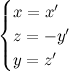
Nessun commento:
Posta un commento