Prendiamo un foglio, con tante belle formule scritte sopra, e fotocopiamolo in modo da ridurlo alle dimensioni di un francobollo. Questa è una trasformazione che certamente non conserva le distanze, e quindi non è una isometria.
La trasformazione base che permette di costruire ingrandimenti o rimpicciolimenti si chiama omotetia, ed è definita una volta fissati un punto (detto centro) e un numero k, che rappresenta il fattore di ingrandimento o rimpicciolimento. Ecco una figurina:
Si costruiscono i segmenti che vanno dal centro C ai vertici della figura (quella rossa), poi questi segmenti devono essere moltiplicati per k (in questa figura k è uguale a 2: i segmenti sono raddoppiati).
La matrice associata a una omotetia avente centro nell'origine e rapporto k è:
Le omotetie di centro C formano un gruppo: l'elemento neutro è l'omotetia che si ottiene per k=1, e l'inverso dell'omotetia di rapporto k è quella di rapporto 1/k. Questo gruppo è però un po' troppo piccolo per poterci fare della geometria, e quindi lo allarghiamo aggiungendovi tutte le isometrie: questo ci consente di spostare le figure in giro per il piano un po' come vogliamo, mentre la solo omotetia ci obbligherebbe a tenere le figure in posizioni ben precise, in modo da avere i vertici allineati col centro.
Il gruppo delle isometrie più le omotetie si chiama gruppo delle similitudini, di cui abbiamo probabilmente sentito parlare, forse alle scuole medie, forse alle superiori. Non ho trovato consenso in giro per la rete per quanto riguarda il nome di questa geometria: qualcuno non associa un nome particolare, qualcun altro la chiama geometria elementare. Chiamiamola così fino a che qualche autorità non interviene a correggere.
Una similitudine non ha, naturalmente, tutti gli invarianti di una isometria. La similitudine non conserva le lunghezze, ad esempio. Nella similitudine si conservano, invece, i rapporti tra le distanze. Quindi le circonferenze vengono trasformate in circonferenze, i segmenti in segmenti, le rette in rette, vengono conservati il parallelismo, la perpendicolarità e le ampiezze degli angoli. Il gruppo delle isometrie è un sottogruppo di quello delle similitudini: questo significa che ogni isometria è anche una similitudine, ma non è vero il viceversa.
E ora cerchiamo di capire il senso di questa suddivisione in tante geometrie. Prendiamo queste due circonferenze:
Non sono uguali, nel senso che non sono composte dagli stessi punti. Non sono uguali nemmeno nel senso della geometria euclidea: non sono cioè congruenti; non esiste nessuna isometria che trasforma una nell'altra. Esse sono invece uguali nel senso della geometria elementare, cioè sono simili.
Quindi in questo tipo di geometria esiste un solo tipo di circonferenza, mentre esistono vari tipi di ellissi, così come esistono vari tipi di rettangoli (ricordiamo la differenza tra un televisore in formato 4:3 e uno in 16:9). Forse non tutti sanno che esiste un solo tipo di parabola: le parabole sono tutte simili tra loro.
La matrice associata a una generica similitudine è questa (dove d è sempre uguale a +1 oppure -1 a seconda del tipo di trasformazione, diretta oppure inversa):
Questo è tutto: per allargare ancora un po' il gruppo, bisogna considerare qualche nuova trasformazione.

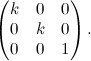

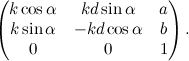
2 commenti:
Ho utilizzato per il mio blog l'immagine dei due cerchi e una vostra frase
"Non sono uguali, nel senso che non sono composte dagli stessi punti. Non sono uguali nemmeno nel senso della geometria euclidea: non sono cioè congruenti; non esiste nessuna isometria che trasforma una nell'altra. Esse sono invece uguali nel senso della geometria elementare, cioè sono simili."
Citando doverosamente il vostro blog e inserendo link di collegamento al vostro blog. Vi passo il link del mio post per una vostra verifica.
http://groviglidiparole.blogspot.it/2012/10/s-similitudini-non-dizionario.html
cordiali saluti
francesco zaffuto
Ok, grazie per la segnalazione
Posta un commento