L'omologia è una trasformazione un po' complicata da spiegare. Vediamo prima un disegno:
Per definire una omologia servono tre elementi: una retta (quella orizzontale nel disegno), una direzione (il vettore) e un numero k (nel disegno ho preso k=2). Poi si procede nel modo seguente: si proietta un qualsiasi punto della figura (il triangolo rosso) sulla retta data, e si moltiplica per k il segmento che va dal punto proiettato sulla retta al punto corrispondente sulla figura. Insomma, il segmento retta-figura blu è il doppio del segmento retta-figura rossa.
Bene, questa roba certamente non è una similitudine: infatti dobbiamo rinunciare a un po' di invarianti. L'ortogonalità non si mantiene più, ma il parallelismo sì. Quindi si può affermare che i parallelogrammi si trasformano in parallelogrammi, ma i rettangoli non rimangono rettangoli.
L'invariante che viene utilizzato in questo tipo di geometria ha un nome strano: si chiama rapporto semplice di tre punti allineati. Dati cioè tre punti A, B e C sulla stessa retta, il rapporto semplice si indica con (A,B,C) ed è uguale a AC/BC (la formula contempla anche i casi di punti coincidenti, e se BC è uguale a zero allora si assegna al rapporto semplice il valore di infinito).
Per poter costruire una nuova geometria dobbiamo combinare queste nuove trasformazioni con le vecchie: se componiamo le omologie con le similitudini, otteniamo il gruppo delle affinità.
Esistono poi alcuni risultati che ci fanno capire qualcosa di più: una qualsiasi affinità si può ottenere componendo una similitudine e al più due omologie. E poi: una qualsiasi affinità si può ottenere componendo una isometria e al più due omologie ortogonali (aventi cioè il vettore ortogonale all'asse) con gli assi ortogonali tra loro. Oppure ancora: una qualsiasi affinità si può ottenere componendo una traslazione più un'altra affinità avente almeno un punto fisso.
Ecco un disegno che rappresenta una omologia ortogonale e che mostra la trasformazione di una circonferenza in una ellisse.
E dunque, dal punto di vista della geometria affine, non c'è differenza tra circonferenza ed ellisse. In questa geometria ci sono solo tre curve di secondo grado diverse: l'ellisse, la parabola e l'iperbole (non tre tipi di curve, ma proprio tre curve in tutto).
La matrice associata a una generica affinità è questa:
dove a, b, c, d, p, q sono numeri qualsiasi (purché la matrice 2×2 che contiene a, b, c, d non abbia determinante nullo). E quindi non c'è spazio per ulteriori generalizzazioni, a meno che non cominciamo a pensare di dare un significato a quella misteriosa terza riga.
Ora viene il bello.


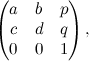
2 commenti:
PGL(2,R), PGL(2,R)!
Arriva, arriva...
Posta un commento