Insomma, sembra che le coordinate omogenee portino solo complicazioni: non solo non c'è più una corrispondenza biunivoca tra punti del piano e coordinate, ma succede anche di peggio: le rette parallele si incontrano. E, tanto per girare il coltello nella piaga, nell'esempio che abbiamo visto si incontrano in un punto la cui terza coordinata è uguale a zero: se ci ricordiamo che la terza coordinata è quel numero che va messo al denominatore, quando dobbiamo risalire dalle coordinate omogenee a quelle normali, siamo a posto.
Bé, in realtà tutti questi problemi sono voluti.
Vediamo di capire il perché con un esempio più generale di quello della volta scorsa: prendiamo due rette parallele,
(ci ricordiamo che due rette parallele hanno lo stesso coefficiente angolare m, vero?) e le trasformiamo in coordinate omogenee,
e le mettiamo a sistema:
Se risolviamo, otteniamo z=0 e y=mx: questo significa che una generica soluzione del sistema può essere scritta come (x,mx,0) o, se vogliamo, (1,m,0).
Quindi due rette parallele si incontrano in un punto la cui terza coordinata è sempre uguale a zero, mentre le prime due godono della seguente proprietà: se poniamo uguale a 1 la prima, la seconda è uguale a m. Detto in termini un po' più pratici: due rette parallele si incontrano in un punto che dipende solo dalla loro direzione.
Cominciamo dunque a fare un po' di ordine: il mondo si divide in due categorie. La prima, quella dei punti normali, è costituita dalle terne la cui terza coordinata è diversa da zero (e che, quindi, grazie al fatto che le coordinate omogenee sono definite a meno di una costante moltiplicativa, possiamo porre uguale a 1). La seconda è costituita dai punti strani, aventi terza coordinata uguale a zero. Questi punti non sono veri punti, ma sono in corrispondenza con tutte le possibili direzioni che le rette possono avere.
La prima categoria, quella dei punti normali, viene detta dei punti propri. La seconda, invece, è quella dei punti impropri.
I punti impropri ci permettono di accedere a un mondo meraviglioso.


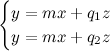
Nessun commento:
Posta un commento