Avevamo detto che c'erano due motivi per cui erano necessarie tre coordinate: uno era perché così le cose funzionano; la spiegazione del secondo motivo era stata rimandata.
Ecco, ora vediamo qual è il secondo motivo: in realtà quelle trasformazioni sono molto più comprensibili se ci mettiamo nel mondo delle coordinate omogenee. Tutte le trasformazioni viste fino ad ora operavano su punti del tipo (x,y,1), che possiamo vedere come punti propri.
Se le generalizziamo a punti di coordinate (x,y,z), senza porre condizioni su z, osserviamo che tali trasformazioni lasciano sempre fissa la retta impropria. Insomma: le affinità (che costituiscono il gruppo di trasformazioni più grande che abbiamo considerato finora) trasformano punti propri in punti propri, e punti impropri in punti impropri.
Il passo successivo è dunque questo: generalizziamo ulteriormente, e consideriamo trasformazioni che mettono in movimento anche la retta impropria. Queste nuove trasformazioni si chiamano proiettività.
La matrice associata a una generica proiettività è semplicemente questa:
Sembrerebbe quindi che le proiettività siano trasformazioni troppo generali da poter avere qualche caratteristica che le contraddistingue, o qualche invariante (l'unica richiesta che viene fatta sulla matrice è che il suo determinante non sia nullo). Non è così: un invariante esiste anche qua, ed ha lo strano nome di birapporto di quattro punti allineati.
È definito in questo modo:
dove con (A,B,C) si intende il rapporto semplice di tre punti allineati, già definito quando abbiamo parlato di affinità.
Bene, le proiettività formano gruppo, che comprende come sottogruppi tutti quelli visti finora, dalle affinità in giù. Con le proiettività ci si diverte un sacco.
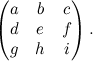
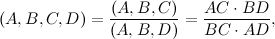
Nessun commento:
Posta un commento