Abbiamo finalmente un gruppo abbastanza grosso da poterci lavorare sopra: quello delle isometrie. La cui matrice associata, nel caso più generale possibile, è la seguente:
dove d vale +1 oppure -1 a seconda del tipo di isometria: +1 per quelle dirette e -1 per quelle inverse.
Una prima considerazione: cosa si intende quando si afferma che due figure sono uguali? Per esempio, due circonferenze con lo stesso raggio sono uguali? Si sarebbe portati a rispondere di sì, ma non è proprio corretto: se le due circonferenze hanno due centri diversi, esse non sono composte dagli stessi punti. Quindi non sono davvero uguali. Se prendo un foglio a quadretti e disegno, in cima alla pagina, un segmento lungo tre quadretti e, in fondo alla pagina, un altro segmento lungo tre quadretti, posso dire che sono uguali? Anche se sono composti da punti che sono tutti diversi?
In un certo senso, le due circonferenze o i due segmenti sono davvero uguali, ma si tratta di capire bene quale sia, questo certo senso. È questa l'idea che sta alla base del programma elaborato Klein.
Abbiamo costruito un gruppo di trasformazioni geometriche, le isometrie. Queste muovono, in tanti modi diversi, i punti del piano: a noi interessa capire se queste trasformazioni hanno qualcosa in comune. Detto in altri termini: a noi interessa capire quali sono gli invarianti di queste trasformazioni. E la parola isometria non è stata scelta a caso: essa ci dice quali caratteristiche vengono mantenute dalle traslazioni, dalle rotazioni, dalle simmetrie e da tutte le loro composizioni.
Le isometrie mantengono le distanze tra i punti.
Se con T indichiamo una generica isometria, la lunghezza del segmento AB è uguale a quella del segmento T(AB).
Due figure che si corrispondono in una isometria si dicono congruenti, o isometriche (o, se vogliamo, anche uguali, ma non nel senso di composte dagli stessi punti; è per questo che si tende a non usare la parola uguali in geometria). Lo studio della congruenza tra figure piane è quello che fa diventare matti gli studenti di prima superiore: la geometria che si ottiene è detta geometria euclidea (anche se negli Elementi di Euclide non compare solo questo tipo di geometria).
Si dimostra che le isometrie trasformano circonferenze in circonferenze, segmenti in segmenti, rette in rette, mantengono il parallelismo, la perpendicolarità e le ampiezze degli angoli. Insomma, godono di tutte quelle proprietà che tanto amiamo.
Ora vediamo di fare a meno di qualcuna di queste proprietà.
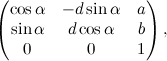
Nessun commento:
Posta un commento