Utilizziamo la proiettività della volta scorsa per trasformare qualche conica. Prendiamo la circonferenza di equazione
che è semplicemente la circonferenza con centro nel punto (0,2) e raggio 1 (se volete saltare i calcoli, più giù c'è la figurina che mostra subito la prospettiva). Dobbiamo trasformarla in coordinate omogenee,
e poi applicare la trasformazione scritta l'altra volta, quella che al posto di x sostituisce x' (cioè non fa nulla), al posto di y sostituisce z' e, al posto di z, sostituisce -y'. Ecco il risultato:
che possiamo riscrivere eliminando gli apici, che ora non servono più, svolgendo un po' i calcoli e rimettendo in coordinate cartesiane. Quello che si ottiene è la seguente formula:
che, se vogliamo scrivere in una forma più utile (per chi ricorda qualcosa di geometria analitica), diventa:
una ellisse, insomma, con centro in (0,-2/3), semiasse maggiore uguale a 1 su radice di 3, semiasse minore uguale a 1 su 3.
Per quelli che hanno saltato i calcoli, ecco la figurina: una circonferenza in prospettiva diventa una ellisse.
Direi che sia una cosa abbastanza naturale, se mi è concesso l'ardire.
Ora trasformiamo qualcosa di meno immediato: una parabola. Precisamente, quella di equazione y=x2+1, che diventa yz=x2+z2 in coordinate omogenee.
Tralascio i passaggi e scrivo subito il risultato: si ottiene la curva x2+y2+y=0 che, scritta in modo da mettere in evidenza centro e raggio, diventa:
Si tratta di una circonferenza con centro in (0,-1/2) e raggio 1/2. Ecco la figura:
Stranamente, una parabola in prospettiva diventa ancora una circonferenza. Questa volta, però, la circonferenza è tangente all'asse delle x, cioè alla linea di orizzonte, cioè alla retta impropria. Insomma, i due rami di parabola non sono proprio come due rette parallele, ma quasi.
Prima di passare all'iperbole, bisogna aggiungere una considerazione. Abbiamo detto che la proiettività che stiamo usando prende ciò che si trova al di sopra dell'asse x e lo mette in prospettiva nella parte sottostante, avendo cioè l'asse x come orizzonte. Naturalmente la trasformazione lavora anche sui punti che si trovano al di sotto dell'asse delle ascisse, anche se finora non abbiamo (volutamente) mai visto un esempio.
Come dobbiamo interpretare l'azione della proiettività nella parte sottostante l'asse delle x? Ecco, è come se noi ci voltassimo dall'altra parte: se finora abbiamo pensato al disegno in prospettiva di ciò che vediamo davanti a noi, ora aggiungiamo anche il disegno di ciò che si trova dietro di noi.
Faccio due disegni, che è meglio. Nel primo, metto solo una parte dell'iperbole di equazione x2-y2=-1, quella che sta di sopra, al posto giusto. E metto anche la funzione trasformata, che è x2+y2=1.
E fin qua possiamo anche essere d'accordo. Ora aggiungo il ramo inferiore dell'iperbole (che si trova nella zona dove noi disegniamo la prospettiva) e la curva trasformata (che si troverà nella parte sopra all'asse delle x). Ecco:
Abbiamo di nuovo una circonferenza, che questa volta attraversa l'orizzonte, cioè la retta impropria.
Riassunto: la prospettiva è un sistema che ci permette di vedere la retta impropria. Mediante il disegno in prospettiva abbiamo capito che le tre categorie di coniche si differenziano solo per il modo in cui vanno all'infinito, cioè intersecano la retta impropria.
L'ellisse non ci va, la retta impropria la vede solo da lontano. La parabola è tangente alla retta impropria, l'iperbole è secante.
Se noi trattiamo la retta impropria come una retta normale, succede che la forma delle tre curve, che ci appare così diversa nella geometria affine, è invece la stessa: sono tutte e tre curve chiuse.
Nella geometria proiettiva esiste una sola conica.
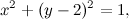
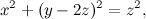
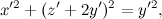
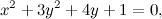
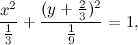





2 commenti:
> Nella geometria proiettiva esiste una sola conica.
Calma. Nella geometria proiettiva complessa (o in quella su un generico campo algebricamente chiuso) esiste solo una conica non degenere, perche' l'unico invariante di congruenza e' il rango.
in P2(R) invece oltre al rango si deve usare anche la segnatura.
Uh. Bè, io facevo un discorso molto divulgativo e non consideravo né coniche degeneri, né coniche a punti complessi (tipo x^2+y^2+1=0). Non sono stato molto preciso, lo ammetto...
Posta un commento