Chi, all'università, studia matematica, o fisica, o qualche ingegneria, probabilmente incontra le matrici per la prima volta nel corso di geometria, l'unica materia che si studia senza fare nemmeno una figura (è così, sembra assurdo ma è così). La definizione di determinante di una matrice è del tutto incomprensibile: provo a scriverla in italiano.
Il determinante di una matrice quadrata n×n è dato dalla somma, fatta su tutte le permutazioni di n elementi, dei prodotti tra il segno della permutazione considerata e gli elementi di ogni riga (o di ogni colonna) riordinati secondo la permutazione stessa.
In formule:
La prima domanda che mi sono fatto io quando ho visto questa definizione è stata: ma come hanno fatto a pensarci? Quale mente malata può produrre una roba del genere? Nessuno te lo spiega, naturalmente, e tu rimani lì a bocca aperta in balia di sentimenti contrastanti: ammirazione per chi ha potuto pensare a una cosa del genere (che funziona, eh, non è scritta a caso) e odio per chi ha potuto pensare a una cosa del genere (che funziona, ma come è possibile che funzioni, santo cielo?).
Prima di provare a dare una spiegazione, ecco una citazione di un famoso matematico, Arnold, uno che faceva disegnini per ogni cosa (disegnava anche gattini) (per spiegare la matematica):
The determinant of a matrix is an (oriented) volume of the parallelepiped whose edges are its columns. If the students are told this secret (which is carefully hidden in the purified algebraic education), then the whole theory of determinants becomes a clear chapter of the theory of poly-linear forms. If determinants are defined otherwise, then any sensible person will forever hate all the determinants, Jacobians and the implicit function theorem.
Ecco. Visto cosa dice sul segreto indicibile riguardante il determinante?
Bene, proviamo allora a capire la definizione geometrica, quella con i disegnini. Partiamo da un parallelogramma:
Potete giocare un po' con l'applet trascinando le punte dei vettori: si vede bene che l'area dipende da quanto sono lunghi i vettori e dall'angolo compreso tra essi (se l'angolo diventa molto piccolo anche l'area diventa piccola). Se i due vettori sono sovrapposti (collineari, come dicono i Veri Matematici), l'area diventa nulla, e in effetti la figura non è più bidimensionale, ma è un segmento.
La stessa cosa vale in tre dimensioni e, se siete capaci di astrarre e diventare Veri Geometri, anche in un numero maggiore di dimensioni.
Il volume diventa uguale a zero quando almeno due dei tre vettori diventano collineari (se ci provate con la figurina qua sopra non è detto che ci riusciate, perché spostare con il mouse una proiezione bidimensionale di un oggetto tridimensionale non è facile. Insomma, il software fa quello che può (e che vuole)).
Ora, quello che vogliamo fare è definire un Coso Matematico che ci permetta di calcolare volumi di oggetti definiti come quelli qui sopra (cioè se parallelogrammi, con due vettori; se parallelepipedi, con tre vettori; se n-parallelotopi (pare che si chiamino così), con n vettori). Come fare?
Prima di tutto, la notazione: immaginiamo che i vettori partano tutti dall'origine, e quindi per definirli ci bastano le coordinate della loro punta. Due coordinate se siamo sul piano, tre coordinate se siamo nello spazio, n coordinate se siamo in spazi di dimensione n. Ecco, queste coordinate le mettiamo in colonna, formando una matrice (se decidessimo di metterle in riga non cambierebbe nulla, ma per fissare le idee pensiamo alle coordinate dei punti scritte in colonna).
Prima regola: un (iper)cubo di lato 1 deve avere area 1. In 2 dimensioni il cubo si chiama quadrato, definito dai vettori aventi estremi in (1,0) e (0,1), e quindi vogliamo definire il determinante in modo che dia come risultato 1 se applicato alla matrice avente come colonne (1,0) e (0,1). Insomma, in formule:
Questo deve valere in generale: in tre dimensioni, ad esempio, avremmo una matrice con tre righe e tre colonne così fatte: (1,0,0), (0,1,0), (0,0,1).
Insomma, abbiamo la
Regola 1: il determinante di una matrice avente 1 sulla diagonale che va dall'alto a sinistra al basso a destra e 0 in tutte le altre caselle deve valere 1. E fin qua ci siamo, andiamo avanti.
D'ora in poi indico con A1, A2, …, An le colonne della matrice (cioè le coordinate delle punte dei vettori).
Poco sopra abbiamo detto che se due vettori sono uguali allora il determinante deve dare zero. Quindi ecco la
Regola 2: det(A1, …, Ai, …, Aj, …, An) = 0 se Ai = Aj per qualche coppia di valori i, j con i diverso da j.
Andiamo avanti: se moltiplichiamo un lato del parallelepipedo per un fattore λ (ai matematici che giocano con le matrici piace molto la lambda, chissà perché), allora il volume deve essere moltiplicato anch'esso per lo stesso valore. Quindi ecco la
Regola 3: det(λA1, …, An) = λdet(A1, …, An) — e questo deve valere per tutte le colonne della matrice, non solo per la prima.
Ora arriva una specie di proprietà distributiva. Cerchiamo di capirla prima con una figura (bidimensionale, così la vediamo meglio, eh):
Anche qua potete spostare le punte dei vettori. L'idea è questa: la somma delle aree dei due parallelogrammi azzurri è uguale a quella di quello rosso (i due triangoli che si formano sopra e sotto sono congruenti, in sostanza)(non fate commenti sui colori). Da qui deduciamo la
Regola 4: det(A1 + B1, …, An) = det(A1, …, An) + det(B1, …, An), e questo deve valere per tutte le colonne, non solo per la prima.
Ebbene, queste quattro regole ci permettono di definire il determinante e di arrivare alla Formulaccia Incomprensibile scritta lassù, basta fare un po' di giochini. Per esempio:
det(A1 + A2, A1 + A2, …, An) deve essere uguale a 0 per la regola 2 (ci sono due colonne uguali), ma se applichiamo per tre volte di seguito la regola 4 abbiamo che
det(A1 + A2, A1 + A2, …, An) =
= det(A1, A1 + A2, …, An) + det(A2, A1 + A2, …, An)
= det(A1, A1, …, An) + det(A1, A2, …, An) + det(A2, A1, …, An) + det(A2, A2, …, An)
= 0 + det(A1, A2, …, An) + det(A2, A1, …, An) + 0,
da cui ricaviamo che det(A1, A2, …, An) + det(A2, A1, …, An) = 0. Ed ecco la
Proprietà 1: scambiando di posto due colonne si inverte il segno del determinante (qui sono state scambiate le prime due, ma potete tranquillamente scambiare quelle che volete). E cambiare l'ordine di due vettori significa cambiare l'orientazione, ecco perché il determinante è il volume orientato del parallelepipedo. Insomma, diamo un significato anche al segno negativo.
Queste regole definiscono il determinante in modo non ambiguo, cioè lo caratterizzano. Vediamo per esempio come si fa per calcolare
Con la notazione usata qui (più comoda per un blog che usa l'html e non il LaTeX), i calcoli sono questi:
A = det((a,c), (b,d)) = det( a(1,0) + c(0,1), b(1,0) + d(0,1))
(applicando la regola 4:)
= det(a(1,0), b(1,0)) + det(a(1,0), d(0,1)) + det(c(0,1), b(1,0)) + det(c(0,1), d(0,1))
(applicando la regola 3;)
= ab[det((1,0), (1,0))] + ad[det((1,0), (0,1)] + bc[det((0,1), (1,0)] + cd[det((0,1), (0,1))]
(applicando la regola 2:)
= ab0 + ad[det((1,0), (0,1)] + bc[det((0,1), (1,0)] + cd0
(applicando la proprietà 1:)
= ad[det((1,0), (0,1)] − bc[det((1,0), (0,1)]
= (ad − bc)[det((1,0),(0,1)]
(applicando la regola 1:)
= ad − bc.
Ecco qua. Come si diceva a scuola: diagonale principale meno diagonale secondaria.
Se si applicano le stesse regole a matrici di ordine superiore ecco che salta fuori la somma fatta sulle permutazioni degli indici di cui si parlava all'inizio. Ora, almeno, c'è un perché che dà un'idea del motivo per cui la definizione sia fatta in quel modo.
Questo non è il percorso storico che ha portato alla definizione di determinante, e si può fare tanta matematica senza avere presente questo aspetto geometrico. Conoscerlo, però, secondo me è meglio.
Credits a Quora, che ogni tanto ha cose interessanti.
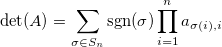
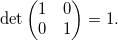

Nessun commento:
Posta un commento