Dopo aver definito le traslazioni e le rotazioni, ci potrebbe venire voglia di combinarle insieme. Che succede se applichiamo una rotazione e una traslazione a un punto (o a una figura)? Possiamo farlo nell'ordine che ci pare? Che trasformazione otteniamo?
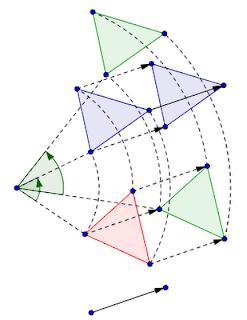
Questa figura (complicata, sì) ci fa capire che la composizione di una rotazione e una traslazione non è commutativa. Proviamo a capire: il percorso con le figure blu ci mostra che la figura rossa viene prima ruotata di un certo angolo, poi traslata secondo un certo vettore. Il percorso con le figure verdi invece ci mostra la figura rossa che prima viene traslata, poi ruotata. Come si vede, i due percorsi non terminano sulla stessa figura: quindi bisogna stare molto attenti all'ordine in cui vengono applicate le trasformazioni.
In realtà, però, non esiste un insieme delle traslazioni+rotazioni, diverso da quello delle rotazioni+traslazioni: la figura qua sotto mostra come sia possibile arrivare alla stessa figura applicando, in un caso, prima una traslazione e poi una rotazione, in un secondo caso invece applicando prima una rotazione e poi una traslazione (diversa dalla precedente, naturalmente).
Quindi esiste un unico gruppo che contiene tutte le possibili composizioni di traslazioni e rotazioni. Questo gruppo, detto delle isometrie dirette (o delle rototraslazioni), contiene i due gruppi di rotazioni e traslazioni (che si dicono essere sottogruppi del gruppo più grande).
La matrice associata a queste trasformazioni è la seguente:
Manca ancora poco per poter parlare della prima geometria.

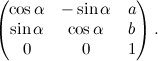
Nessun commento:
Posta un commento