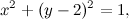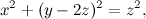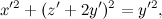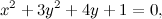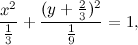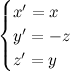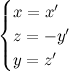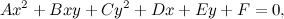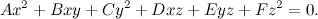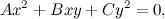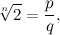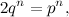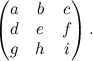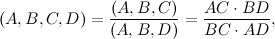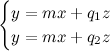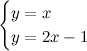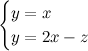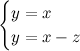martedì 28 settembre 2010
Sistemi di riferimento e relatività galileiana
Il PSSC ha prodotto, ormai troppi anni fa, una serie di filmati riguardanti i principali argomenti della fisica. Questo è uno dei più belli, date un'occhiata almeno all'inizio (peccato per quella pubblicità che compare proprio al centro del video).
mercoledì 22 settembre 2010
Erlangen 1872 — Un modello per il piano proiettivo
Non è facile visualizzare il piano proiettivo. Facciamo fatica non solo perché i punti impropri sono all'infinito, e ci riesce difficile vedere fin là, ma anche a causa di una strana proprietà di cui godono questi benedetti punti.
La sostanza è questa: una retta possiede un solo punto improprio, ma va all'infinito seguendo due direzioni opposte. Detto in altri termini, due persone che si trovano su una retta e camminano verso l'infinito andando verso due direzioni opposte, arrivano allo stesso punto. È come se le rette possedessero una natura circolare.
Il disegno in prospettiva non ci aiuta nel visualizzare il piano proiettivo nella sua totalità: effettivamente ci permette di vedere la retta impropria, perché essa diventa la linea di orizzonte, ma questo non basta. Se la retta impropria è diventata propria, assumendo il ruolo di orizzonte, un'altra retta che prima era propria ha preso il suo posto. Insomma, una proiettività non può far diventare propria la retta impropria senza trovare un'altra retta che la sostituisca.
Se il piano proiettivo è formato dal piano euclideo usuale più la retta impropria, noi avremmo bisogno di qualcosa che comprima il tutto nella zona finita, e che non lasci nulla all'infinito. Un modello del piano proiettivo in cui tutto è visibile da occhi umani.
Bene, modelli di questo tipo esistono, ma sono molto strani.
Prima di tutto, abbiamo bisogno di una dimensione in più: per vedere il piano proiettivo abbiamo bisogno dello spazio normale (cioè euclideo). In secondo luogo, l'apparente natura circolare propria di ogni retta viene esplicitata utilizzando una sfera.
Siccome l'animazione aiuta molto di più di qualche disegnino, ecco un filmato che mostra come associare i punti di un piano a quelli di una sfera.
Le rette diventano cerchi massimi di una sfera (cioè circonferenze che stanno sulla sfera e hanno, come centro, il centro della sfera), e due cerchi massimi si incontrano sempre: anche se le corrispondenti rette sono parallele, essi si intersecano comunque, purtroppo in due punti. Dico purtroppo perché noi ne vorremmo uno solo, di punti di intersezione. Dato che invece ne abbiamo due (che sono sempre antipodali), dobbiamo compiere un'ulteriore operazione di astrazione: i punti antipodali sulla sfera devono essere identificati. Li dobbiamo immaginare come se fossero lo stesso punto: siamo ancora di fronte a quella apparente circolarità della retta di cui abbiamo parlato prima.
Se riusciamo a immaginare i punti antipodali come un solo punto, e i cerchi massimi come rette, siamo a posto: quello della sfera è un modello del piano proiettivo.
Altrimenti, se non ci piace il fatto di avere due punti che dobbiamo identificare mentalmente, possiamo costruire una figura in cui questi punti vengono effettivamente identificati.
Prendiamo la sfera e tagliamola a metà: in questo modo gettiamo via quasi tutti i punti doppi. Ci rimangono solo quelli del bordo, che devono essere identificati a due a due.
Cominciamo a prendere il bordo e a piegarlo, in modo da fare corrispondere ogni punto con quello diametralmente opposto.
E alla fine richiudiamo il tutto: purtroppo, per poter fare coincidere ogni punto con quello antipodale, è necessario che la superficie si autointersechi.
La figura che otteniamo si chiama cross-cap. Se andate sulla pagina di mathworld, trovate una applicazione java che vi permette di esaminare il cross-cap girandolo come vi pare.
Insomma, non si scappa: o ci immaginiamo la sfera in cui due punti sono uno solo, o ci prendiamo il cross-cap con la superficie che interseca sé stessa. Oppure passiamo in quattro dimensioni. TANSTAAFL.
(Direi che possiamo fermarci qua, con il programma di Erlangen)
La sostanza è questa: una retta possiede un solo punto improprio, ma va all'infinito seguendo due direzioni opposte. Detto in altri termini, due persone che si trovano su una retta e camminano verso l'infinito andando verso due direzioni opposte, arrivano allo stesso punto. È come se le rette possedessero una natura circolare.
Il disegno in prospettiva non ci aiuta nel visualizzare il piano proiettivo nella sua totalità: effettivamente ci permette di vedere la retta impropria, perché essa diventa la linea di orizzonte, ma questo non basta. Se la retta impropria è diventata propria, assumendo il ruolo di orizzonte, un'altra retta che prima era propria ha preso il suo posto. Insomma, una proiettività non può far diventare propria la retta impropria senza trovare un'altra retta che la sostituisca.
Se il piano proiettivo è formato dal piano euclideo usuale più la retta impropria, noi avremmo bisogno di qualcosa che comprima il tutto nella zona finita, e che non lasci nulla all'infinito. Un modello del piano proiettivo in cui tutto è visibile da occhi umani.
Bene, modelli di questo tipo esistono, ma sono molto strani.
Prima di tutto, abbiamo bisogno di una dimensione in più: per vedere il piano proiettivo abbiamo bisogno dello spazio normale (cioè euclideo). In secondo luogo, l'apparente natura circolare propria di ogni retta viene esplicitata utilizzando una sfera.
Siccome l'animazione aiuta molto di più di qualche disegnino, ecco un filmato che mostra come associare i punti di un piano a quelli di una sfera.
Le rette diventano cerchi massimi di una sfera (cioè circonferenze che stanno sulla sfera e hanno, come centro, il centro della sfera), e due cerchi massimi si incontrano sempre: anche se le corrispondenti rette sono parallele, essi si intersecano comunque, purtroppo in due punti. Dico purtroppo perché noi ne vorremmo uno solo, di punti di intersezione. Dato che invece ne abbiamo due (che sono sempre antipodali), dobbiamo compiere un'ulteriore operazione di astrazione: i punti antipodali sulla sfera devono essere identificati. Li dobbiamo immaginare come se fossero lo stesso punto: siamo ancora di fronte a quella apparente circolarità della retta di cui abbiamo parlato prima.
Se riusciamo a immaginare i punti antipodali come un solo punto, e i cerchi massimi come rette, siamo a posto: quello della sfera è un modello del piano proiettivo.
Altrimenti, se non ci piace il fatto di avere due punti che dobbiamo identificare mentalmente, possiamo costruire una figura in cui questi punti vengono effettivamente identificati.
Prendiamo la sfera e tagliamola a metà: in questo modo gettiamo via quasi tutti i punti doppi. Ci rimangono solo quelli del bordo, che devono essere identificati a due a due.
Insomma, non si scappa: o ci immaginiamo la sfera in cui due punti sono uno solo, o ci prendiamo il cross-cap con la superficie che interseca sé stessa. Oppure passiamo in quattro dimensioni. TANSTAAFL.
(Direi che possiamo fermarci qua, con il programma di Erlangen)
martedì 21 settembre 2010
Erlangen 1872 — Dualità
La magia che fa corrispondere punti a rette e rette a punti si chiama dualità. Ed è una magia molto potente, perché permette di avere teoremi gratis e, cosa forse ancora più importante, permette di avere una visione nuova della geometria: una di quelle esperienze a-ha di cui ha parlato anche il Sommo Divulgatore.
Provo a fare qualche esempio.
Due punti individuano una retta (detto in altri termini: per due punti passa una e una sola retta). Scambiando i punti con le rette, otteniamo la proposizione due rette individuano un punto (cioè: due rette si intersecano sempre in un punto).
Per un punto passano infinite rette, che diventa una retta contiene infiniti punti.
Insomma, ogni teorema può essere trasformato in un altro teorema scambiando tra loro i termini punto e retta. Naturalmente cambiano anche i verbi che vengono usati: un punto appartiene a una retta, una retta passa per un punto, ma la relazione che intercorre tra il punto e la retta è una sola, e viene detta struttura di incidenza.
Vediamo un esempio un po' più corposo.
Dati tre punti allineati A, B e C e altri tre punti allineati a, b e c, allora i punti X, Y e Z, rispettivamente intersezioni delle rette Ab e aB, Ac e aC, Bc e bC, sono anch'essi allineati.
Che diventa, applicando la dualità:
Date tre rette A, B e C incidenti, e altre tre rette a, b e c anch'esse incidenti, allora le rette X, Y e Z, rispettivamente passanti per i punti di intersezione di A con b e di a con B, di A con c e di a con C, di B con c e di b con C sono anch'esse incidenti.
Un altro esempio:
Sono dati due triangoli ABC e A'B'C'. Se le rette AA', BB' e CC' sono incidenti, allora le rette AB e A'B', BC e B'C', CA e C'A' si intersecano rispettivamente in tre punti X, Y e Z che sono allineati.
Vediamo di dualizzarlo:
Sono dati due triangoli ABC e A'B'C'. Se tre punti X, Y e Z sono allineati e, rispettivamente, si trovano sul prolungamento di AB e A'B', BC e B'C', CA e C'A', allora le tre rette AA', BB' e CC' sono incidenti.
Insomma, questo teorema è duale di sé stesso.
Bello, eh?
Provo a fare qualche esempio.
Due punti individuano una retta (detto in altri termini: per due punti passa una e una sola retta). Scambiando i punti con le rette, otteniamo la proposizione due rette individuano un punto (cioè: due rette si intersecano sempre in un punto).
Per un punto passano infinite rette, che diventa una retta contiene infiniti punti.
Insomma, ogni teorema può essere trasformato in un altro teorema scambiando tra loro i termini punto e retta. Naturalmente cambiano anche i verbi che vengono usati: un punto appartiene a una retta, una retta passa per un punto, ma la relazione che intercorre tra il punto e la retta è una sola, e viene detta struttura di incidenza.
Vediamo un esempio un po' più corposo.
Dati tre punti allineati A, B e C e altri tre punti allineati a, b e c, allora i punti X, Y e Z, rispettivamente intersezioni delle rette Ab e aB, Ac e aC, Bc e bC, sono anch'essi allineati.
Che diventa, applicando la dualità:
Date tre rette A, B e C incidenti, e altre tre rette a, b e c anch'esse incidenti, allora le rette X, Y e Z, rispettivamente passanti per i punti di intersezione di A con b e di a con B, di A con c e di a con C, di B con c e di b con C sono anch'esse incidenti.
Un altro esempio:
Sono dati due triangoli ABC e A'B'C'. Se le rette AA', BB' e CC' sono incidenti, allora le rette AB e A'B', BC e B'C', CA e C'A' si intersecano rispettivamente in tre punti X, Y e Z che sono allineati.
Vediamo di dualizzarlo:
Sono dati due triangoli ABC e A'B'C'. Se tre punti X, Y e Z sono allineati e, rispettivamente, si trovano sul prolungamento di AB e A'B', BC e B'C', CA e C'A', allora le tre rette AA', BB' e CC' sono incidenti.
Insomma, questo teorema è duale di sé stesso.
Bello, eh?
lunedì 20 settembre 2010
Erlangen 1872 — È una specie di magia
Un punto ha due coordinate, e fin qua niente di strano: due numeri individuano un punto sul piano cartesiano.
Una retta ha equazione y=mx+q. Per determinare una retta, quindi, bisogna conoscere i due numeri m e q. Due numeri individuano una retta sul piano cartesiano.
Quindi se io scrivo 3 e 14, potrei voler descrivere un punto oppure una retta. Oppure tutte e due.
In realtà le cose non stanno proprio così: non tutte le rette hanno la forma y=mx+q, quelle verticali si scrivono in un'altra maniera: x=k. Ma possiamo evitare il problema passando alle coordinate omogenee.
Ricominciamo: un punto ha tre coordinate, (a,b,c), definite a meno di una costante.
Una retta ha equazione ax+by+c=0, dove i coefficienti a, b e c sono definiti a meno di una costante.
Quindi tre numeri a, b e c definiscono, a meno di una costante moltiplicativa, un punto o, indifferentemente, una retta. O tutte e due.
Detto in un altro modo: ad ogni punto è associata una retta, e ad ogni retta è associato un punto. Il mondo dei punti potrebbe essere trasformato nel mondo delle rette e, viceversa, il mondo delle rette potrebbe diventare quello dei punti. Anche le rette, quindi, hanno delle coordinate, che vengono dette coordinate plückeriane.
Esempio: (3,1,4).
Se le consideriamo come coordinate omogenee di un punto, trasformandole in coordinate cartesiane otteniamo il punto (3/4,1/4).
Se invece le consideriamo come coordinate plückeriane, esse rappresentano la retta 3x+y+4z=0. Ecco qua:
C'è una relazione geometrica tra il punto e la retta: se noi tracciamo, dall'origine O degli assi, la perpendicolare alla retta data, e indichiamo con H il punto di intersezione, risulta che il punto P si trova sulla stessa perpendicolare, in una posizione tale per cui PO è il reciproco di OH.
Viceversa, se partiamo dal punto e tracciamo una retta passante per P e O, la retta cercata sarà ortogonale a PO, e l'intersezione tra le due rette H è tale per cui OH è il reciproco di PO.
E il tutto funziona anche coi punti impropri! A un punto improprio corrisponde una retta passante per l'origine, e viceversa.
Ma tutto questo non basta: consideriamo un'altra coppia punto-retta, per esempio quella identificata dalla terna (-1,2,1). Indichiamo con Q il nuovo punto:
Ora tracciamo la retta passante per P e Q: quale sarà il suo punto associato? Ebbene, non è un punto a caso, ma è l'intersezione tra le due rette che abbiamo già tracciato.
E se le rette sono parallele? Nessun problema, ci sono i punti impropri.
Tutto ciò è meraviglioso.
Una retta ha equazione y=mx+q. Per determinare una retta, quindi, bisogna conoscere i due numeri m e q. Due numeri individuano una retta sul piano cartesiano.
Quindi se io scrivo 3 e 14, potrei voler descrivere un punto oppure una retta. Oppure tutte e due.
In realtà le cose non stanno proprio così: non tutte le rette hanno la forma y=mx+q, quelle verticali si scrivono in un'altra maniera: x=k. Ma possiamo evitare il problema passando alle coordinate omogenee.
Ricominciamo: un punto ha tre coordinate, (a,b,c), definite a meno di una costante.
Una retta ha equazione ax+by+c=0, dove i coefficienti a, b e c sono definiti a meno di una costante.
Quindi tre numeri a, b e c definiscono, a meno di una costante moltiplicativa, un punto o, indifferentemente, una retta. O tutte e due.
Detto in un altro modo: ad ogni punto è associata una retta, e ad ogni retta è associato un punto. Il mondo dei punti potrebbe essere trasformato nel mondo delle rette e, viceversa, il mondo delle rette potrebbe diventare quello dei punti. Anche le rette, quindi, hanno delle coordinate, che vengono dette coordinate plückeriane.
Esempio: (3,1,4).
Se le consideriamo come coordinate omogenee di un punto, trasformandole in coordinate cartesiane otteniamo il punto (3/4,1/4).
Se invece le consideriamo come coordinate plückeriane, esse rappresentano la retta 3x+y+4z=0. Ecco qua:
C'è una relazione geometrica tra il punto e la retta: se noi tracciamo, dall'origine O degli assi, la perpendicolare alla retta data, e indichiamo con H il punto di intersezione, risulta che il punto P si trova sulla stessa perpendicolare, in una posizione tale per cui PO è il reciproco di OH.
Viceversa, se partiamo dal punto e tracciamo una retta passante per P e O, la retta cercata sarà ortogonale a PO, e l'intersezione tra le due rette H è tale per cui OH è il reciproco di PO.
E il tutto funziona anche coi punti impropri! A un punto improprio corrisponde una retta passante per l'origine, e viceversa.
Ma tutto questo non basta: consideriamo un'altra coppia punto-retta, per esempio quella identificata dalla terna (-1,2,1). Indichiamo con Q il nuovo punto:
E se le rette sono parallele? Nessun problema, ci sono i punti impropri.
Tutto ciò è meraviglioso.
domenica 19 settembre 2010
sabato 18 settembre 2010
Erlangen 1872 — Esiste una sola conica
Utilizziamo la proiettività della volta scorsa per trasformare qualche conica. Prendiamo la circonferenza di equazione
che è semplicemente la circonferenza con centro nel punto (0,2) e raggio 1 (se volete saltare i calcoli, più giù c'è la figurina che mostra subito la prospettiva). Dobbiamo trasformarla in coordinate omogenee,
e poi applicare la trasformazione scritta l'altra volta, quella che al posto di x sostituisce x' (cioè non fa nulla), al posto di y sostituisce z' e, al posto di z, sostituisce -y'. Ecco il risultato:
che possiamo riscrivere eliminando gli apici, che ora non servono più, svolgendo un po' i calcoli e rimettendo in coordinate cartesiane. Quello che si ottiene è la seguente formula:
che, se vogliamo scrivere in una forma più utile (per chi ricorda qualcosa di geometria analitica), diventa:
una ellisse, insomma, con centro in (0,-2/3), semiasse maggiore uguale a 1 su radice di 3, semiasse minore uguale a 1 su 3.
Per quelli che hanno saltato i calcoli, ecco la figurina: una circonferenza in prospettiva diventa una ellisse.
Direi che sia una cosa abbastanza naturale, se mi è concesso l'ardire.
Ora trasformiamo qualcosa di meno immediato: una parabola. Precisamente, quella di equazione y=x2+1, che diventa yz=x2+z2 in coordinate omogenee.
Tralascio i passaggi e scrivo subito il risultato: si ottiene la curva x2+y2+y=0 che, scritta in modo da mettere in evidenza centro e raggio, diventa:
Si tratta di una circonferenza con centro in (0,-1/2) e raggio 1/2. Ecco la figura:
Stranamente, una parabola in prospettiva diventa ancora una circonferenza. Questa volta, però, la circonferenza è tangente all'asse delle x, cioè alla linea di orizzonte, cioè alla retta impropria. Insomma, i due rami di parabola non sono proprio come due rette parallele, ma quasi.
Prima di passare all'iperbole, bisogna aggiungere una considerazione. Abbiamo detto che la proiettività che stiamo usando prende ciò che si trova al di sopra dell'asse x e lo mette in prospettiva nella parte sottostante, avendo cioè l'asse x come orizzonte. Naturalmente la trasformazione lavora anche sui punti che si trovano al di sotto dell'asse delle ascisse, anche se finora non abbiamo (volutamente) mai visto un esempio.
Come dobbiamo interpretare l'azione della proiettività nella parte sottostante l'asse delle x? Ecco, è come se noi ci voltassimo dall'altra parte: se finora abbiamo pensato al disegno in prospettiva di ciò che vediamo davanti a noi, ora aggiungiamo anche il disegno di ciò che si trova dietro di noi.
Faccio due disegni, che è meglio. Nel primo, metto solo una parte dell'iperbole di equazione x2-y2=-1, quella che sta di sopra, al posto giusto. E metto anche la funzione trasformata, che è x2+y2=1.
E fin qua possiamo anche essere d'accordo. Ora aggiungo il ramo inferiore dell'iperbole (che si trova nella zona dove noi disegniamo la prospettiva) e la curva trasformata (che si troverà nella parte sopra all'asse delle x). Ecco:
Abbiamo di nuovo una circonferenza, che questa volta attraversa l'orizzonte, cioè la retta impropria.
Riassunto: la prospettiva è un sistema che ci permette di vedere la retta impropria. Mediante il disegno in prospettiva abbiamo capito che le tre categorie di coniche si differenziano solo per il modo in cui vanno all'infinito, cioè intersecano la retta impropria.
L'ellisse non ci va, la retta impropria la vede solo da lontano. La parabola è tangente alla retta impropria, l'iperbole è secante.
Se noi trattiamo la retta impropria come una retta normale, succede che la forma delle tre curve, che ci appare così diversa nella geometria affine, è invece la stessa: sono tutte e tre curve chiuse.
Nella geometria proiettiva esiste una sola conica.
che è semplicemente la circonferenza con centro nel punto (0,2) e raggio 1 (se volete saltare i calcoli, più giù c'è la figurina che mostra subito la prospettiva). Dobbiamo trasformarla in coordinate omogenee,
e poi applicare la trasformazione scritta l'altra volta, quella che al posto di x sostituisce x' (cioè non fa nulla), al posto di y sostituisce z' e, al posto di z, sostituisce -y'. Ecco il risultato:
che possiamo riscrivere eliminando gli apici, che ora non servono più, svolgendo un po' i calcoli e rimettendo in coordinate cartesiane. Quello che si ottiene è la seguente formula:
che, se vogliamo scrivere in una forma più utile (per chi ricorda qualcosa di geometria analitica), diventa:
Per quelli che hanno saltato i calcoli, ecco la figurina: una circonferenza in prospettiva diventa una ellisse.
Direi che sia una cosa abbastanza naturale, se mi è concesso l'ardire.
Ora trasformiamo qualcosa di meno immediato: una parabola. Precisamente, quella di equazione y=x2+1, che diventa yz=x2+z2 in coordinate omogenee.
Tralascio i passaggi e scrivo subito il risultato: si ottiene la curva x2+y2+y=0 che, scritta in modo da mettere in evidenza centro e raggio, diventa:
Si tratta di una circonferenza con centro in (0,-1/2) e raggio 1/2. Ecco la figura:
Stranamente, una parabola in prospettiva diventa ancora una circonferenza. Questa volta, però, la circonferenza è tangente all'asse delle x, cioè alla linea di orizzonte, cioè alla retta impropria. Insomma, i due rami di parabola non sono proprio come due rette parallele, ma quasi.
Prima di passare all'iperbole, bisogna aggiungere una considerazione. Abbiamo detto che la proiettività che stiamo usando prende ciò che si trova al di sopra dell'asse x e lo mette in prospettiva nella parte sottostante, avendo cioè l'asse x come orizzonte. Naturalmente la trasformazione lavora anche sui punti che si trovano al di sotto dell'asse delle ascisse, anche se finora non abbiamo (volutamente) mai visto un esempio.
Come dobbiamo interpretare l'azione della proiettività nella parte sottostante l'asse delle x? Ecco, è come se noi ci voltassimo dall'altra parte: se finora abbiamo pensato al disegno in prospettiva di ciò che vediamo davanti a noi, ora aggiungiamo anche il disegno di ciò che si trova dietro di noi.
Faccio due disegni, che è meglio. Nel primo, metto solo una parte dell'iperbole di equazione x2-y2=-1, quella che sta di sopra, al posto giusto. E metto anche la funzione trasformata, che è x2+y2=1.
Abbiamo di nuovo una circonferenza, che questa volta attraversa l'orizzonte, cioè la retta impropria.
Riassunto: la prospettiva è un sistema che ci permette di vedere la retta impropria. Mediante il disegno in prospettiva abbiamo capito che le tre categorie di coniche si differenziano solo per il modo in cui vanno all'infinito, cioè intersecano la retta impropria.
L'ellisse non ci va, la retta impropria la vede solo da lontano. La parabola è tangente alla retta impropria, l'iperbole è secante.
Se noi trattiamo la retta impropria come una retta normale, succede che la forma delle tre curve, che ci appare così diversa nella geometria affine, è invece la stessa: sono tutte e tre curve chiuse.
Nella geometria proiettiva esiste una sola conica.
venerdì 17 settembre 2010
Non ce la posso fare
Dopo una settimana di lezione, ancora non mi capacito di avere studenti dell'età di mio figlio maggiore.
Erlangen 1872 — Prospettiva
Facciamo un esempio. Prendiamo questa proiettività, dalle equazioni molto semplici:
Dobbiamo interpretare le equazioni in questo modo: noi abbiamo le coordinate (omogenee) di un punto (x,y,z), le inseriamo nelle formule e otteniamo le coordinate del punto trasformato (x',y',z').
Ora prendiamo questi quattro punti: A(-1,1,1), B(1,1,1), C(1,3,1) e D(-1,3,1), e li trasformiamo. Utilizzando le formule della proiettività, otteniamo A'(-1,-1,1), B'(1,-1,1), e fin qua è facile. Quando andiamo a fare i conti per C', risulta (1,-1,3): se ci ricordiamo che le coordinate sono omogenee, e quindi possiamo moltiplicare o dividere ogni termine per una costante arbitraria, possiamo scrivere che C' ha coordinate (1/3,-1/3,1), così lo possiamo rappresentare meglio. Analogamente per D' otteniamo (-1/3,-1/3,1).
Ecco un disegno:
Si capisce come agisce la trasformazione? Prende ciò che si trova al di sopra dell'asse x e lo rappresenta in prospettiva di sotto: in questo caso l'asse x diventa la linea d'orizzonte; le rette parallele BC e AD convergono in un punto. In pratica questa proiettività prende la retta impropria e la sposta al posto dell'asse x.
Ecco un altro esempio:
La figura ABCD è un rettangolo, le cui coordinate sono le seguenti: A(0,1), B(1,3), C(-3,5), D(-4,3). Se volete fare i conti, i punti trasformati sono A'(0,-1), B'(1/3,-1/3), C'(-3/5,-1/5), D'(-4/3,-1/3). Il rettangolo ha i lati opposti paralleli secondo due direzioni diverse, quindi AB e DC si incontrano nello stesso punto improprio, mentre BC e AD si incontrano in un punto improprio diverso (sono quelli che, in disegno tecnico, si chiamano punti di fuga): ecco un ingrandimento della figura in prospettiva.
Bene, trasformare i punti è facile. Ora vorremmo trasformare delle curve. È altrettanto facile purché capiamo una cosa: se la curva ha equazione f(x,y)=0, noi non possiamo prendere i suoi infiniti punti e trasformarli uno per uno, e allora giriamo il problema: prendiamo le equazioni della trasformazione geometrica e le inseriamo nella curva. Occorre quindi un passaggio preliminare, molto semplice: dobbiamo ricavare le coordinate x,y,z in funzione di x',y',z'.
Questa è quindi la trasformazione da usare per trasformare delle curve:
Trasformare alcune coniche sarà molto simpatico.
Dobbiamo interpretare le equazioni in questo modo: noi abbiamo le coordinate (omogenee) di un punto (x,y,z), le inseriamo nelle formule e otteniamo le coordinate del punto trasformato (x',y',z').
Ora prendiamo questi quattro punti: A(-1,1,1), B(1,1,1), C(1,3,1) e D(-1,3,1), e li trasformiamo. Utilizzando le formule della proiettività, otteniamo A'(-1,-1,1), B'(1,-1,1), e fin qua è facile. Quando andiamo a fare i conti per C', risulta (1,-1,3): se ci ricordiamo che le coordinate sono omogenee, e quindi possiamo moltiplicare o dividere ogni termine per una costante arbitraria, possiamo scrivere che C' ha coordinate (1/3,-1/3,1), così lo possiamo rappresentare meglio. Analogamente per D' otteniamo (-1/3,-1/3,1).
Ecco un disegno:
Ecco un altro esempio:
Questa è quindi la trasformazione da usare per trasformare delle curve:
Trasformare alcune coniche sarà molto simpatico.
giovedì 16 settembre 2010
Erlangen 1872 — Intersezioni con la retta impropria
Abbiamo detto che l'equazione di una conica è una generica equazione di secondo grado in due incognite:
che in coordinate omogenee diventa:
Se ora intersechiamo con la retta impropria (che ha equazione z=0), otteniamo:
che è una equazione di secondo grado facilmente risolvibile con la solita formula. Come succede per tutte le equazioni di secondo grado, sono possibili tre casi:
— due soluzioni reali distinte: in questo caso la conica ha due punti impropri diversi, e quindi è una iperbole;
— due soluzioni reali coincidenti: in questo caso la conica è tangente alla retta impropria, ed è una parabola;
— nessuna soluzione reale: ecco l'ellisse.
Insomma, le coniche si riconoscono dal tipo di intersezione che hanno con la retta impropria. O, se vogliamo, per come vanno all'infinito.
Sarà meglio fare qualche disegnino.
Se ora intersechiamo con la retta impropria (che ha equazione z=0), otteniamo:
che è una equazione di secondo grado facilmente risolvibile con la solita formula. Come succede per tutte le equazioni di secondo grado, sono possibili tre casi:
— due soluzioni reali distinte: in questo caso la conica ha due punti impropri diversi, e quindi è una iperbole;
— due soluzioni reali coincidenti: in questo caso la conica è tangente alla retta impropria, ed è una parabola;
— nessuna soluzione reale: ecco l'ellisse.
Insomma, le coniche si riconoscono dal tipo di intersezione che hanno con la retta impropria. O, se vogliamo, per come vanno all'infinito.
Sarà meglio fare qualche disegnino.
mercoledì 15 settembre 2010
Erlangen 1872 — Coniche e retta impropria
Le rette sono tutte rappresentabili da equazioni di primo grado nelle due incognite x e y; viceversa, ogni equazione in due incognite rappresenta una retta (purché l'equazione non sia una roba strana e impossibile come 1=0).
Quindi le rette sono fatte così: ax+by+c=0 (con a e b non contemporaneamente uguali a zero).
Ora passiamo alle equazioni di secondo grado. Prima di tutto: come sono fatte? Ricordando che le incognite sono due, e che quindi esiste anche il termine xy, di secondo grado, una generica equazione è fatta così:
Ax2+Bxy+Cy2+Dx+Ey+F=0.
Bene: le coniche sono tutte equazioni di secondo grado. Vale anche il viceversa se consideriamo coniche anche oggetti strani come x2+y2=-1, che è una equazione che non rappresenta niente (non esistono valori di x e di y che la soddisfano) e che ci permettiamo dunque di chiamare circonferenza immaginaria. Ci sono anche oggetti un po' meno strani, come per esempio x2-y2=0, che si trasforma in (x+y)(x-y)=0, e che geometricamente è interpretabile come l'insieme di due rette: la chiamiamo iperbole degenere — in pratica è una iperbole coincidente con i propri asintoti, è come se noi prendessimo un cono e lo tagliassimo con un piano che lo attraversa e passa anche per il suo vertice.
Ecco un'immagine che ci mostra una iperbole degenere:
E, già che ci siamo, ecco una parabola degenere (cioè due rette coincidenti):
Ed ecco una ellisse, o circonferenza, degenere (in pratica è un punto solo soletto):
Ora la domanda è: come riconosciamo se una generica equazione di secondo grado rappresenta una iperbole, una parabola o una ellisse? Qui ci viene in aiuto la retta impropria.
La sostanza è questa: una ellisse è una curva tranquilla, chiusa, la vediamo tutta, non fugge lontano: la retta impropria non sa neanche cosa sia. Una iperbole, al contrario, va all'infinito, e ci va oltretutto lungo due direzioni diverse: quindi incontra la retta impropria, e lo fa in due punti. Una parabola è una via di mezzo: va all'infinito, ma ci va lungo la stessa direzione, per così dire: tocca cioè la retta impropria in un solo punto.
Ora vediamo i calcoli.
Quindi le rette sono fatte così: ax+by+c=0 (con a e b non contemporaneamente uguali a zero).
Ora passiamo alle equazioni di secondo grado. Prima di tutto: come sono fatte? Ricordando che le incognite sono due, e che quindi esiste anche il termine xy, di secondo grado, una generica equazione è fatta così:
Ax2+Bxy+Cy2+Dx+Ey+F=0.
Bene: le coniche sono tutte equazioni di secondo grado. Vale anche il viceversa se consideriamo coniche anche oggetti strani come x2+y2=-1, che è una equazione che non rappresenta niente (non esistono valori di x e di y che la soddisfano) e che ci permettiamo dunque di chiamare circonferenza immaginaria. Ci sono anche oggetti un po' meno strani, come per esempio x2-y2=0, che si trasforma in (x+y)(x-y)=0, e che geometricamente è interpretabile come l'insieme di due rette: la chiamiamo iperbole degenere — in pratica è una iperbole coincidente con i propri asintoti, è come se noi prendessimo un cono e lo tagliassimo con un piano che lo attraversa e passa anche per il suo vertice.
Ecco un'immagine che ci mostra una iperbole degenere:
E, già che ci siamo, ecco una parabola degenere (cioè due rette coincidenti):
La sostanza è questa: una ellisse è una curva tranquilla, chiusa, la vediamo tutta, non fugge lontano: la retta impropria non sa neanche cosa sia. Una iperbole, al contrario, va all'infinito, e ci va oltretutto lungo due direzioni diverse: quindi incontra la retta impropria, e lo fa in due punti. Una parabola è una via di mezzo: va all'infinito, ma ci va lungo la stessa direzione, per così dire: tocca cioè la retta impropria in un solo punto.
Ora vediamo i calcoli.
martedì 14 settembre 2010
Primo giorno di scuola
La migliore battuta su facebook dopo il primo giorno di lezione (oggi):
-1: l'estate si avvicina
lunedì 13 settembre 2010
Erlangen 1872 — Coniche, similitudini e affinità
Le circonferenze sono tutte simili, le parabole anche, le ellissi e le iperboli no.
Intuitivamente, diremmo che queste due ellissi hanno forma diversa, una è più schiacciata dell'altra: si dice che hanno eccentricità diversa. Non si può ingrandire la più piccola per farla diventare uguale a quella più grande: non esiste nessuna similitudine che porta una nell'altra.
Anche per una iperbole vale lo stesso discorso, anche se è più difficile da capire: in figura, oltre all'iperbole, sono rappresentati altri oggetti. Le due rette tratteggiate corrispondono al profilo del cono dal quale è stata ritagliata l'iperbole: si chiamano asintoti e sono due rette che approssimano l'iperbole, man mano che la curva si allontana dal centro. Il rettangolo è quello che ci dà la forma dell'iperbole: una similitudine permette di trasformare un'iperbole in un'altra avente un rettangolo simile a quello di partenza. Cambiando le proporzioni del rettangolo, cambiano le iperboli.
Riassumendo: se ci mettiamo nella geometria delle similitudini, esiste un'unica parabola, esistono tante ellissi diverse, ed esistono tante iperboli diverse.
Se invece passiamo alle affinità, le cose sono più semplici: tutte le ellissi sono trasformabili una nell'altra, e così pure tutte le iperboli (e naturalmente tutte le parabole, dato che bastava una similitudine). Quindi nella geometria affine esistono una sola parabola, una sola ellisse e una sola iperbole. La circonferenza fa naturalmente parte della famiglia delle ellissi.
Ora vediamo un'altra caratteristica comune a tutte le coniche.
Anche per una iperbole vale lo stesso discorso, anche se è più difficile da capire: in figura, oltre all'iperbole, sono rappresentati altri oggetti. Le due rette tratteggiate corrispondono al profilo del cono dal quale è stata ritagliata l'iperbole: si chiamano asintoti e sono due rette che approssimano l'iperbole, man mano che la curva si allontana dal centro. Il rettangolo è quello che ci dà la forma dell'iperbole: una similitudine permette di trasformare un'iperbole in un'altra avente un rettangolo simile a quello di partenza. Cambiando le proporzioni del rettangolo, cambiano le iperboli.
Riassumendo: se ci mettiamo nella geometria delle similitudini, esiste un'unica parabola, esistono tante ellissi diverse, ed esistono tante iperboli diverse.
Se invece passiamo alle affinità, le cose sono più semplici: tutte le ellissi sono trasformabili una nell'altra, e così pure tutte le iperboli (e naturalmente tutte le parabole, dato che bastava una similitudine). Quindi nella geometria affine esistono una sola parabola, una sola ellisse e una sola iperbole. La circonferenza fa naturalmente parte della famiglia delle ellissi.
Ora vediamo un'altra caratteristica comune a tutte le coniche.
sabato 11 settembre 2010
Erlangen 1872 — Coniche
Circonferenza, parabola, ellisse, iperbole: tutte queste curve fanno parte della categoria delle coniche. Perché?
Partiamo dalla definizione: cosa sono quelle curve? Cosa hanno in comune, e quali sono le differenze?
Prima di tutto: esistono due modi per definirle. Sono luoghi di punti, e sono sezioni di cono.
Per esempio, una circonferenza è il luogo dei punti equidistanti da un punto (che viene detto centro). Guardando la figura, per ogni punto P la distanza PO rimane costante.
Una ellisse è il luogo dei punti per i quali rimane costante la somma delle due distanze da due punti (che vengono detti fuochi). Sempre facendo riferimento alla figura, la somma PF1+PF2 rimane costante.
Una parabola è il luogo dei punti equidistanti da un punto (detto fuoco) e da una retta (detta direttrice). In figura, PF è uguale a PH:
E infine, una iperbole è il luogo dei punti per i quali rimane costante la differenza in valore assoluto delle distanze tra due punti (detti fuochi). In figura, |PF1 - PF2| è costante:
Tutte queste curve sono anche definibili in un altro modo. Prendiamo quello che si definisce cono circolare retto, il che significa che dobbiamo prendere una retta, tenerla stretta per un punto e farla ruotare con una certa ampiezza. Quello che otteniamo è una cosa del genere:
Ora cominciamo a tagliare a fette questo doppio cono: a seconda dell'inclinazione del nostro coltello, possiamo ottenere figure diverse.
Se il piano secante è parallelo alla generatrice del cono (diciamo che la generatrice è il lato, ma non ditelo in una interrogazione) abbiamo la figura 1: una parabola. Se il piano forma un angolo sufficientemente grande con l'asse del cono (maggiore di quello formato dalla generatrice) siamo nel caso 2: una ellisse. La circonferenza è un caso particolare: si ottiene quando il piano è perpendicolare alla generatrice. Se il piano forma un angolo piccolo con l'asse del cono (minore di quello formato dalla generatrice) abbiamo una iperbole: questo è il caso 3. Ecco perché queste curve si chiamano coniche: perché si ottengono tutte come sezioni dello stesso cono.
Bene, ora ripensiamo alle isometrie: che succede se trasformiamo una conica con una isometria?
La risposta è: niente di speciale: una circonferenza rimarrà una circonferenza, una ellisse rimarrà una ellisse, e così vale per le parabole e le iperboli. Non solo: una circonferenza non verrà trasformata in una circonferenza di raggio diverso, una ellisse non verrà trasformata in una ellisse con assi di lunghezze diverse, una parabola manterrà costante la distanza tra fuoco e direttrice, e una iperbole manterrà costante la distanza tra i fuochi (e un'altra caratteristica che si chiama asse immaginario, sulla quale non ci fermiamo troppo: diciamo che nemmeno l'iperbole cambia forma).
La prossima volta vediamo cosa combinano le similitudini e le affinità.
Partiamo dalla definizione: cosa sono quelle curve? Cosa hanno in comune, e quali sono le differenze?
Prima di tutto: esistono due modi per definirle. Sono luoghi di punti, e sono sezioni di cono.
Per esempio, una circonferenza è il luogo dei punti equidistanti da un punto (che viene detto centro). Guardando la figura, per ogni punto P la distanza PO rimane costante.
Tutte queste curve sono anche definibili in un altro modo. Prendiamo quello che si definisce cono circolare retto, il che significa che dobbiamo prendere una retta, tenerla stretta per un punto e farla ruotare con una certa ampiezza. Quello che otteniamo è una cosa del genere:
Bene, ora ripensiamo alle isometrie: che succede se trasformiamo una conica con una isometria?
La risposta è: niente di speciale: una circonferenza rimarrà una circonferenza, una ellisse rimarrà una ellisse, e così vale per le parabole e le iperboli. Non solo: una circonferenza non verrà trasformata in una circonferenza di raggio diverso, una ellisse non verrà trasformata in una ellisse con assi di lunghezze diverse, una parabola manterrà costante la distanza tra fuoco e direttrice, e una iperbole manterrà costante la distanza tra i fuochi (e un'altra caratteristica che si chiama asse immaginario, sulla quale non ci fermiamo troppo: diciamo che nemmeno l'iperbole cambia forma).
La prossima volta vediamo cosa combinano le similitudini e le affinità.
venerdì 10 settembre 2010
Un semplice esercizio
Teorema: per ogni n maggiore di 2, 
è irrazionale.
Dimostrazione:
Supponiamo per assurdo che la radice n-esima di 2 sia razionale: allora può essere scritta come frazione nel modo seguente:
con p e q interi positivi. Elevando alla n ed eliminando il denominatore, si ottiene l'espressione
che può essere riscritta così:
Un teoremino dimostrato da Andrew Wiles ci fa concludere che p e q non esistono. C.V.D.
(Via: 360, ctk)
è irrazionale.Dimostrazione:
Supponiamo per assurdo che la radice n-esima di 2 sia razionale: allora può essere scritta come frazione nel modo seguente:
che può essere riscritta così:
Un teoremino dimostrato da Andrew Wiles ci fa concludere che p e q non esistono. C.V.D.
(Via: 360, ctk)
Erlangen 1872 — Proiettività
Quando abbiamo scritto per la prima volta le equazioni di una trasformazione geometrica, abbiamo detto che la matrice associata era una matrice 3×3, e non 2×2, per cui un generico punto doveva essere scritto come terna (x,y,1) e non come coppia (x,y).
Avevamo detto che c'erano due motivi per cui erano necessarie tre coordinate: uno era perché così le cose funzionano; la spiegazione del secondo motivo era stata rimandata.
Ecco, ora vediamo qual è il secondo motivo: in realtà quelle trasformazioni sono molto più comprensibili se ci mettiamo nel mondo delle coordinate omogenee. Tutte le trasformazioni viste fino ad ora operavano su punti del tipo (x,y,1), che possiamo vedere come punti propri.
Se le generalizziamo a punti di coordinate (x,y,z), senza porre condizioni su z, osserviamo che tali trasformazioni lasciano sempre fissa la retta impropria. Insomma: le affinità (che costituiscono il gruppo di trasformazioni più grande che abbiamo considerato finora) trasformano punti propri in punti propri, e punti impropri in punti impropri.
Il passo successivo è dunque questo: generalizziamo ulteriormente, e consideriamo trasformazioni che mettono in movimento anche la retta impropria. Queste nuove trasformazioni si chiamano proiettività.
La matrice associata a una generica proiettività è semplicemente questa:
Sembrerebbe quindi che le proiettività siano trasformazioni troppo generali da poter avere qualche caratteristica che le contraddistingue, o qualche invariante (l'unica richiesta che viene fatta sulla matrice è che il suo determinante non sia nullo). Non è così: un invariante esiste anche qua, ed ha lo strano nome di birapporto di quattro punti allineati.
È definito in questo modo:
dove con (A,B,C) si intende il rapporto semplice di tre punti allineati, già definito quando abbiamo parlato di affinità.
Bene, le proiettività formano gruppo, che comprende come sottogruppi tutti quelli visti finora, dalle affinità in giù. Con le proiettività ci si diverte un sacco.
Avevamo detto che c'erano due motivi per cui erano necessarie tre coordinate: uno era perché così le cose funzionano; la spiegazione del secondo motivo era stata rimandata.
Ecco, ora vediamo qual è il secondo motivo: in realtà quelle trasformazioni sono molto più comprensibili se ci mettiamo nel mondo delle coordinate omogenee. Tutte le trasformazioni viste fino ad ora operavano su punti del tipo (x,y,1), che possiamo vedere come punti propri.
Se le generalizziamo a punti di coordinate (x,y,z), senza porre condizioni su z, osserviamo che tali trasformazioni lasciano sempre fissa la retta impropria. Insomma: le affinità (che costituiscono il gruppo di trasformazioni più grande che abbiamo considerato finora) trasformano punti propri in punti propri, e punti impropri in punti impropri.
Il passo successivo è dunque questo: generalizziamo ulteriormente, e consideriamo trasformazioni che mettono in movimento anche la retta impropria. Queste nuove trasformazioni si chiamano proiettività.
La matrice associata a una generica proiettività è semplicemente questa:
Sembrerebbe quindi che le proiettività siano trasformazioni troppo generali da poter avere qualche caratteristica che le contraddistingue, o qualche invariante (l'unica richiesta che viene fatta sulla matrice è che il suo determinante non sia nullo). Non è così: un invariante esiste anche qua, ed ha lo strano nome di birapporto di quattro punti allineati.
È definito in questo modo:
dove con (A,B,C) si intende il rapporto semplice di tre punti allineati, già definito quando abbiamo parlato di affinità.
Bene, le proiettività formano gruppo, che comprende come sottogruppi tutti quelli visti finora, dalle affinità in giù. Con le proiettività ci si diverte un sacco.
giovedì 9 settembre 2010
Erlangen 1872 — Retta impropria
Che cosa rappresenta l'equazione x=0?
È quella retta avente tutti i punti con ascissa uguale a zero, cioè è l'asse delle y.
Come si trasforma l'equazione se la mettiamo in coordinate omogenee?
Dato che non ci sono termini noti, in coordinate omogenee l'asse delle y ha sempre equazione x=0. Facile.
Cosa possiamo dire riguardo l'equazione y=0? Analogamente a quanto detto prima, y=0 è l'equazione dell'asse delle x, scritta sia in coordinate non omogenee che in coordinate omogenee. Facile.
Se ci mettiamo in coordinate omogenee, cosa rappresenta l'equazione z=0?
Ecco la novità: z=0 è una equazione di primo grado, e dunque siamo autorizzati a chiamarla retta. Ma qual è la caratteristica comune di tutti i suoi punti? Hanno tutti la terza coordinata uguale a zero, quindi sono tutti punti impropri. La retta di equazione z=0 viene detta retta impropria, e non è disegnabile sul piano cartesiano. Molti dicono che assomiglia a una circonferenza con raggio infinito e centro nell'origine, e in un certo senso hanno ragione.
Esiste però un modo per visualizzarla: basta cambiare punto di vista.
Nella realtà le righe blu del quadro qua sopra sarebbero parallele, eppure si incontrano tutte in un punto. Bene, quello è il punto improprio comune a tutte le rette blu. Dove si trova? Sulla linea dell'orizzonte: ecco, quella è la retta impropria. Ogni punto della linea dell'orizzonte rappresenta una diversa direzione.
Queste considerazioni ci consentono di aprire le porte della geometria proiettiva.
È quella retta avente tutti i punti con ascissa uguale a zero, cioè è l'asse delle y.
Come si trasforma l'equazione se la mettiamo in coordinate omogenee?
Dato che non ci sono termini noti, in coordinate omogenee l'asse delle y ha sempre equazione x=0. Facile.
Cosa possiamo dire riguardo l'equazione y=0? Analogamente a quanto detto prima, y=0 è l'equazione dell'asse delle x, scritta sia in coordinate non omogenee che in coordinate omogenee. Facile.
Se ci mettiamo in coordinate omogenee, cosa rappresenta l'equazione z=0?
Ecco la novità: z=0 è una equazione di primo grado, e dunque siamo autorizzati a chiamarla retta. Ma qual è la caratteristica comune di tutti i suoi punti? Hanno tutti la terza coordinata uguale a zero, quindi sono tutti punti impropri. La retta di equazione z=0 viene detta retta impropria, e non è disegnabile sul piano cartesiano. Molti dicono che assomiglia a una circonferenza con raggio infinito e centro nell'origine, e in un certo senso hanno ragione.
Esiste però un modo per visualizzarla: basta cambiare punto di vista.
Nella realtà le righe blu del quadro qua sopra sarebbero parallele, eppure si incontrano tutte in un punto. Bene, quello è il punto improprio comune a tutte le rette blu. Dove si trova? Sulla linea dell'orizzonte: ecco, quella è la retta impropria. Ogni punto della linea dell'orizzonte rappresenta una diversa direzione.
Queste considerazioni ci consentono di aprire le porte della geometria proiettiva.
mercoledì 8 settembre 2010
Erlangen 1872 — Punti impropri
Insomma, sembra che le coordinate omogenee portino solo complicazioni: non solo non c'è più una corrispondenza biunivoca tra punti del piano e coordinate, ma succede anche di peggio: le rette parallele si incontrano. E, tanto per girare il coltello nella piaga, nell'esempio che abbiamo visto si incontrano in un punto la cui terza coordinata è uguale a zero: se ci ricordiamo che la terza coordinata è quel numero che va messo al denominatore, quando dobbiamo risalire dalle coordinate omogenee a quelle normali, siamo a posto.
Bé, in realtà tutti questi problemi sono voluti.
Vediamo di capire il perché con un esempio più generale di quello della volta scorsa: prendiamo due rette parallele,
(ci ricordiamo che due rette parallele hanno lo stesso coefficiente angolare m, vero?) e le trasformiamo in coordinate omogenee,
e le mettiamo a sistema:
Se risolviamo, otteniamo z=0 e y=mx: questo significa che una generica soluzione del sistema può essere scritta come (x,mx,0) o, se vogliamo, (1,m,0).
Quindi due rette parallele si incontrano in un punto la cui terza coordinata è sempre uguale a zero, mentre le prime due godono della seguente proprietà: se poniamo uguale a 1 la prima, la seconda è uguale a m. Detto in termini un po' più pratici: due rette parallele si incontrano in un punto che dipende solo dalla loro direzione.
Cominciamo dunque a fare un po' di ordine: il mondo si divide in due categorie. La prima, quella dei punti normali, è costituita dalle terne la cui terza coordinata è diversa da zero (e che, quindi, grazie al fatto che le coordinate omogenee sono definite a meno di una costante moltiplicativa, possiamo porre uguale a 1). La seconda è costituita dai punti strani, aventi terza coordinata uguale a zero. Questi punti non sono veri punti, ma sono in corrispondenza con tutte le possibili direzioni che le rette possono avere.
La prima categoria, quella dei punti normali, viene detta dei punti propri. La seconda, invece, è quella dei punti impropri.
I punti impropri ci permettono di accedere a un mondo meraviglioso.
Bé, in realtà tutti questi problemi sono voluti.
Vediamo di capire il perché con un esempio più generale di quello della volta scorsa: prendiamo due rette parallele,
(ci ricordiamo che due rette parallele hanno lo stesso coefficiente angolare m, vero?) e le trasformiamo in coordinate omogenee,
e le mettiamo a sistema:
Se risolviamo, otteniamo z=0 e y=mx: questo significa che una generica soluzione del sistema può essere scritta come (x,mx,0) o, se vogliamo, (1,m,0).
Quindi due rette parallele si incontrano in un punto la cui terza coordinata è sempre uguale a zero, mentre le prime due godono della seguente proprietà: se poniamo uguale a 1 la prima, la seconda è uguale a m. Detto in termini un po' più pratici: due rette parallele si incontrano in un punto che dipende solo dalla loro direzione.
Cominciamo dunque a fare un po' di ordine: il mondo si divide in due categorie. La prima, quella dei punti normali, è costituita dalle terne la cui terza coordinata è diversa da zero (e che, quindi, grazie al fatto che le coordinate omogenee sono definite a meno di una costante moltiplicativa, possiamo porre uguale a 1). La seconda è costituita dai punti strani, aventi terza coordinata uguale a zero. Questi punti non sono veri punti, ma sono in corrispondenza con tutte le possibili direzioni che le rette possono avere.
La prima categoria, quella dei punti normali, viene detta dei punti propri. La seconda, invece, è quella dei punti impropri.
I punti impropri ci permettono di accedere a un mondo meraviglioso.
martedì 7 settembre 2010
Erlangen 1872 — Convergenze parallele
Si tratta di fare un passo ardito. Ma, per capire bene, bisogna fare qualche calcoletto.
Prendiamo l'equazione di una retta, per esempio y=x: è una equazione molto semplice, che rappresenta la bisettrice del primo e del terzo quadrante.
Prendiamone un'altra, per esempio y=2x-1. Se le rappresentiamo sul piano, otteniamo questo grafico:
Sono due rette secanti; se vogliamo trovare le coordinate del loro punto di intersezione, dobbiamo risolvere il sistema tra le due equazioni, che è il seguente:
Con una semplice sostituzione si trova la soluzione, che è proprio x=1, y=1, come si vede anche dal grafico.
Bene: rifacciamo i calcoli in coordinate omogenee.
Come si trasformano le equazioni? Non è difficile: ogni volta che si trova una x si sostituisce x/z, e ogni volta che si trova una y si sostituisce y/z. Quindi le equazioni delle due rette diventerebbero:
E ora il passo ardito: eliminiamo i denominatori senza porci troppi problemi, e rimettiamo a sistema il tutto;
Cosa è successo? Prima di tutto l'equazione di una delle due rette è cambiata, e in secondo luogo abbiamo un sistema in tre equazioni e due incognite. Vediamo di capirci qualcosa.
Primo fatto: se l'equazione originale non aveva termine noto (si dice che era omogenea), allora trasformandola in coordinate omogenee non cambia. Infatti senza termini noti si osserva che z è un denominatore comune, che si può togliere senza scrupoli (se per caso capita da queste parti uno studente di prima superiore: normalmente questa semplificazione è considerata un errore, servono le condizioni di esistenza, eh).
Se l'equazione originale invece aveva termine noto (cioè era non omogenea), la trasformazione in coordinate omogenee la fa diventare omogenea (guarda un po'). Insomma, il termine noto acquisisce una z.
Secondo fatto: un sistema di due equazioni in tre incognite non ha un unico risultato, di solito: ci sono troppe incognite. Se proviamo a risolvere per sostituzione il sistema scritto sopra, otteniamo x=z, e non abbiamo ulteriori equazioni per determinare il valore di z. La soluzione del sistema, utilizzando queste nuove coordinate, diventa quindi (z,z,z). Dividendo tutto per z, otteniamo (1,1,1). Che, in coordinate omogenee, rappresenta il punto (1,1).
Riassunto: abbiamo effettivamente complicato le cose semplici.
Ma allora, perchè lo facciamo?
La risposta è data dal seguente esempio. Proviamo a calcolare l'intersezione tra le due rette y=x e y=x-1.
Le due rette sono parallele, quindi non hanno intersezione. Effettivamente, il sistema tra le loro due equazioni, in coordinate cartesiane, è impossibile. E quello in coordinate omogenee?
Eccolo qua:
Sostituendo x al posto di y nella seconda equazione, otteniamo z=0. Quindi questo sistema ammette soluzione! Tutte le terne del tipo (x,x,0) vanno bene. Dividendo per x, otteniamo ad esempio come soluzione il punto (1,1,0). Quindi il sistema tra le equazioni delle due rette parallele ha soluzione.
Quindi due rette parallele si incontrano in un punto. E buonanotte a Euclide.
Prendiamo l'equazione di una retta, per esempio y=x: è una equazione molto semplice, che rappresenta la bisettrice del primo e del terzo quadrante.
Prendiamone un'altra, per esempio y=2x-1. Se le rappresentiamo sul piano, otteniamo questo grafico:
Bene: rifacciamo i calcoli in coordinate omogenee.
Come si trasformano le equazioni? Non è difficile: ogni volta che si trova una x si sostituisce x/z, e ogni volta che si trova una y si sostituisce y/z. Quindi le equazioni delle due rette diventerebbero:
E ora il passo ardito: eliminiamo i denominatori senza porci troppi problemi, e rimettiamo a sistema il tutto;
Cosa è successo? Prima di tutto l'equazione di una delle due rette è cambiata, e in secondo luogo abbiamo un sistema in tre equazioni e due incognite. Vediamo di capirci qualcosa.
Primo fatto: se l'equazione originale non aveva termine noto (si dice che era omogenea), allora trasformandola in coordinate omogenee non cambia. Infatti senza termini noti si osserva che z è un denominatore comune, che si può togliere senza scrupoli (se per caso capita da queste parti uno studente di prima superiore: normalmente questa semplificazione è considerata un errore, servono le condizioni di esistenza, eh).
Se l'equazione originale invece aveva termine noto (cioè era non omogenea), la trasformazione in coordinate omogenee la fa diventare omogenea (guarda un po'). Insomma, il termine noto acquisisce una z.
Secondo fatto: un sistema di due equazioni in tre incognite non ha un unico risultato, di solito: ci sono troppe incognite. Se proviamo a risolvere per sostituzione il sistema scritto sopra, otteniamo x=z, e non abbiamo ulteriori equazioni per determinare il valore di z. La soluzione del sistema, utilizzando queste nuove coordinate, diventa quindi (z,z,z). Dividendo tutto per z, otteniamo (1,1,1). Che, in coordinate omogenee, rappresenta il punto (1,1).
Riassunto: abbiamo effettivamente complicato le cose semplici.
Ma allora, perchè lo facciamo?
La risposta è data dal seguente esempio. Proviamo a calcolare l'intersezione tra le due rette y=x e y=x-1.
Le due rette sono parallele, quindi non hanno intersezione. Effettivamente, il sistema tra le loro due equazioni, in coordinate cartesiane, è impossibile. E quello in coordinate omogenee?
Eccolo qua:
Sostituendo x al posto di y nella seconda equazione, otteniamo z=0. Quindi questo sistema ammette soluzione! Tutte le terne del tipo (x,x,0) vanno bene. Dividendo per x, otteniamo ad esempio come soluzione il punto (1,1,0). Quindi il sistema tra le equazioni delle due rette parallele ha soluzione.
Quindi due rette parallele si incontrano in un punto. E buonanotte a Euclide.
Iscriviti a:
Post (Atom)