Si fa presto a dire cina /3

Dopo le classifiche basate sul rapporto medaglie/abitanti, ecco un altro argomento su cui meditare. Come stabilire l'ordinamento in classifica dei vari stati? Perché, ad esempio, dieci medaglie d'oro e una d'argento dovrebbero essere meglio di nove medaglie d'oro e cinquanta d'argento? Come sarebbe meglio ordinare le terne di medaglie?

Si potrebbe privilegiare il totale delle medaglie, e usare le medaglie d'oro per gli spareggi (in questo caso, 9 ori e 50 argenti sono meglio di 10 ori e 1 argento). Oppure si potrebbero privilegiare gli ori, usando gli argenti e i bronzi come spareggio. Esistono anche altri sistemi intermedi tra questi due: si può assegnare un punteggio alle medaglie d'oro, un secondo punteggio più basso del primo agli argenti, e un terzo ancora minore ai bronzi. Per esempio, si potrebbe stabilire che ogni medaglia d'oro vale 3 punti, ogni argento 2 e ogni bronzo 1.

Un vero matematico, a dir la verità, preferirebbe proporre un punteggio pari, ad esempio, a π² per l'oro, π per l'argento e 1 per il bronzo, in modo da non avere parità se non nel caso in cui due stati riescano ad ottenere esattamente le stesse medaglie.

Questi diversi sistemi producono, purtroppo, classifiche diverse. È possibile stilare una classifica che metta tutti d'accordo?

In questa pagina viene proposto un nuovo tipo di ordinamento, che idealmente potrebbe essere condiviso da tutti, e che si basa sulle seguenti leggi:

• il numero di medaglie conta, a parità di altri fattori: se uno stato A ha ottenuto almeno tanti ori, almeno tanti argenti e almeno tanti bronzi di quanti ne abbia ottenuto uno stato B, allora i due stati sono almeno pari in classifica,
• oro è meglio di argento, argento è meglio di bronzo: se lo stato A ha ottenuto un argento in più e un bronzo in meno dello stato B, allora deve essere più in alto in classifica. Infatti B, per ottenere lo stesso risultato di A, dovrebbe fare meglio in una specialità in cui ha vinto il bronzo e riuscire a ottenere l'argento.

Diciamo allora che uno stato A è stato migliore di un altro stato B se il medagliere di B può essere trasformato nel medagliere di A mediante una sequenza di aggiunte di medaglie oppure di sostituzione di medaglie basse con medaglie alte.

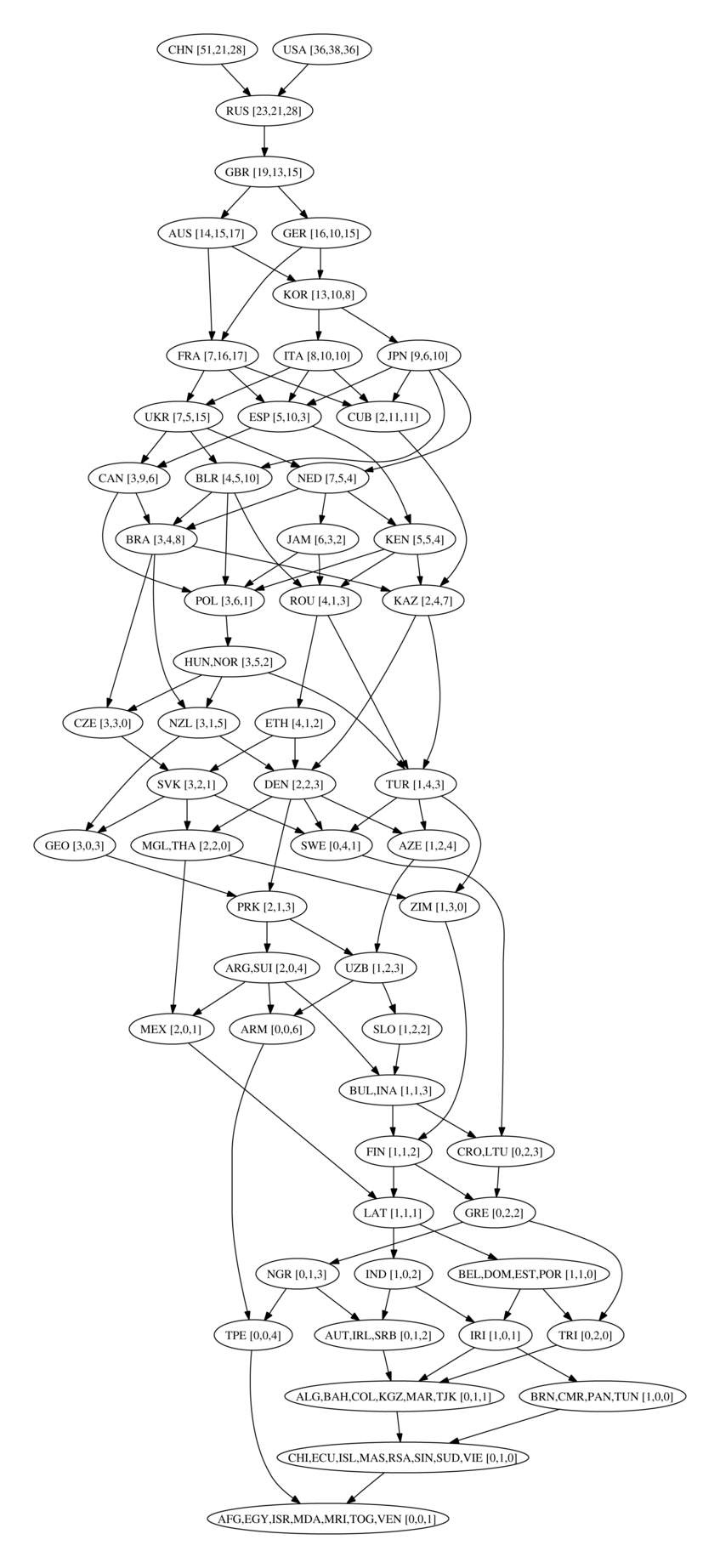
Per esempio, indicando con una terna di numeri le medaglie ottenute, ordinando dall'oro al bronzo, l'Inghilterra ha ottenuto (19,13,15), mentre l'Austria (14,15,17). Sostituiamo 2 medaglie di bronzo dell'Austria con 2 d'argento, ottenendo (14,17,15). Ora sostituiamo 4 argenti con altrettanti ori, arrivando a (18,13,15). Ora dobbiamo aggiungere un oro per arrivare a (19,13,15), quindi l'Austria ha fatto peggio dell'Inghilterra.

Quello che abbiamo ottenuto è un ordinamento parziale: non è detto che due medaglieri siano sempre confrontabili. Per esempio, non lo sono Cina (51,21,28) e Stati Uniti (36,38,36). Ma l'ordinamento che si ottiene dovrebbe mettere d'accordo tutti.

Questo è il risultato: