Ogni ordinale è dunque l'insieme che contiene tutti gli ordinali minori di esso, e questo insieme è bene ordinato. Inoltre gli ordinali finiti corrispondono ai numeri naturali. Poi ci sono gli ordinali transfiniti.
“Esistono anche quelli?”.
“Certo. Dato che esistono insiemi infiniti e dato che ogni insieme è bene ordinabile, a ogni insieme dotato di ordinamento puoi associare un ordinale, così come abbiamo fatto con i cardinali”.
“Ah. E quindi anche in questo caso dovremo usare simboli che non sono numeri?”.
“Eh sì. Ora definiamo un ordinale transfinito, il più semplice. Associato all'insieme infinito più semplice, quello dei numeri naturali”.
“Sono pronto”.
“Ricorderai questa serie di definizioni:”.
0 = {}
1 = {0}
2 = {0,1}
3 = {0,1,2}
...
“Sì, certo. Ogni ordinale è l'insieme di tutti gli ordinali che lo precedono”.
“Bene. Ora, l'insieme dei numeri naturali può essere visto come un insieme di ordinali”.
“Sì, direi l'insieme di tutti gli ordinali finiti”.
“Ok. Allora definiamo l'ordinale ω in questo modo: ω = {0,1,2,3,...}”.
“Bé, mi pare di capire che questo ordinale sia l'insieme dei numeri naturali”.
“È così, come l'ordinale 4 è l'insieme {0,1,2,3}”.
“Va bene, ma non lo avevamo chiamato ℵ0?”.
“Oh, no. Con ℵ0 avevamo indicato solo la cardinalità dell'insieme dei naturali, non abbiamo mai parlato dell'ordinamento. Esistono insiemi di cardinalità ℵ0 che però corrispondono a un ordinale diverso da ω”.
“Uh? Vorrei un esempio”.
“Va bene, ma prima ti farò un esempio di un insieme diverso da quello dei naturali che corrisponde sempre allo stesso numero ordinale”.
“Va bene, vai”.
“Considera questo insieme: {Piccolino, 0,1,2,...}”.
“Carino, è l'insieme dei numeri naturali ai quali hai aggiunto Piccolino. Ma ha sempre cardinalità ℵ0, come insegna il paradosso dell'albergo di Hilbert”.
“Giusto. Devi però osservare che ho aggiunto un elemento all'interno di un insieme ordinato, e quindi ho specificato anche come funziona l'ordinamento per questo nuovo elemento: in pratica, Piccolino è minore di tutti gli altri numeri”.
“Va bene, avresti potuto chiamarlo -1, però”.
“Certo, ma preferisco così per analogia con l'esempio che ti farò dopo”.
“Allora ok, chiamiamolo Piccolino”.
“Questo insieme, allora, è in corrispondenza biunivoca con quello dei naturali?”.
“Sì, certo, come con l'albergo di Hilbert. Basta spostare tutti i numeri di una posizione per fare posto a Piccolino. In questo modo mantengo anche l'ordinamento”.
“E quindi, anche questo insieme corrisponde al numero ordinale ω”
“Sì, giusto”.
“Ora considera quest'altro insieme: {0,1,2,...,Gigante}”.
“Uhm, cosa c'è al posto di quei puntini?”.
“L'elenco di tutti i numeri naturali. Prevengo la tua obiezione: avere scritto Gigante dopo infiniti numeri significa che Gigante, nell'ordinamento dei naturali, è maggiore di qualunque altro numero”.
“Uhm, mi pare di capire. Anche questo insieme ha cardinalità ℵ0, però...”.
“Però?”.
“Però non riesco più a fare una corrispondenza biunivoca che mantiene l'ordine”.
“Perché no?”.
“Perché non so dove sistemare quel Gigante. Se devo mantenere l'ordine, dovrei farlo corrispondere con un numero naturale maggiore di tutti gli altri. Solo che questo numero non esiste”.
“Bravo. Hai capito che questo insieme non corrisponde all'ordinale ω”.
“E a quale ordinale corrisponde?”.
“Te lo dico dopo che avremo imparato a fare le operazioni”.
martedì 30 settembre 2008
lunedì 29 settembre 2008
Verso l'infinito, ma con calma - numeri ordinali
Avevamo accennato a due modi di contare: i numeri cardinali tengono conto della grandezza di un insieme, mentre i numeri ordinali tengono conto dell'ordine con cui compaiono gli elementi che voglio contare.
La cardinalità, abbiamo visto, è una proprietà degli insiemi. Con i numeri ordinali, invece, vogliamo tenere conto anche delle relazioni d'ordine che sono definite sugli insiemi che stiamo considerando.
È necessaria, ed importante, una prima definizione: un insieme si dice bene ordinato se ogni suo sottoinsieme ammette un primo elemento.
“Cominciamo con gli esempi?”.
“Ok. Prendi l'insieme dei numeri naturali, con l'ordinamento usuale”.
“Bene. Poi?”.
“Poi prendi un qualunque suo sottoinsieme, finito o infinito, non importa”.
“Ok. Prendiamo {42,272,314}”.
“Domanda: è vero che ammette un primo elemento? Cioè, è vero che ha minimo?”.
“Certo: 42”.
“Ed è vero che questa proprietà è valida per ogni sottoinsieme, anche se infinito?”.
“Direi di sì, se è infinito contiene elementi sempre più grandi, ma un minimo c'è”.
“Perfetto. Quindi diciamo che l'insieme dei numeri naturali, dotato dell'ordinamento usuale, è bene ordinato”.
“Ok. E se cambio insieme?”.
“Se ricordi, ne avevamo già parlato. Se ammettiamo come vero l'assioma della scelta, ogni insieme è bene ordinabile”.
“Mh, è vero. Avevi anche detto che nessuno è riuscito a trovare un buon ordinamento per i numeri reali”.
“Esatto”.
“Però nemmeno i numeri interi sono bene ordinabili. Se prendo un insieme che contiene infiniti numeri negativi, questo non ha minimo”.
“Vero, ma questo non significa che gli interi non sono bene ordinabili, ma solo che l'ordinamento che stai considerando non è un buon ordinamento”.
“In che senso? Potrei cambiarlo?”.
“Certo. Prova a considerare questo nuovo ordinamento degli interi: {0,1,-1,2,-2,3,-3,...}”.
“Ah! Vedo, questo è un buon ordinamento, a sinistra mi fermo”.
“Perfetto. Ora facciamo un passo avanti. Ricordi le funzioni biunivoche?”.
“Certo, allora la matematica mi sembrava più semplice”.
“Bene, quando parliamo di insiemi ordinati, potremmo desiderare che una funzione biunivoca tra due insiemi preservi l'ordine”.
“Uhm, servirebbe un altro esempio”.
“Prendiamo due insiemi ordinati, per esempio {1,2,3} e {Qua, Paperino, Paperone}”.
“Ehm, capisco l'ordinamento del primo insieme, ma non capisco bene quello del secondo...”.
“Diciamo che è quello dell'età. I tre personaggi sono ordinati in base alla loro età”.
“Va bene. Secondo quanto ho imparato, sono due insiemi di cardinalità 3, ed esiste una corrispondenza biunivoca tra uno e l'altro”.
“Ottimo. Ora ti propongo questa corrispondenza:”.
“Certamente è biunivoca”.
“Infatti. Però non preserva l'ordine. Puoi vedere che 2 è minore di 3, ma f(2), cioè Paperone, non è minore di f(3), cioè Paperino”.
“Ho capito, ora è chiaro. Se vuoi fare una corrispondenza biunivoca che conserva l'ordine devi scrivere questo:”.
“Bene. Ora, se ricordi, avevamo definito i numeri cardinali con le relazioni di equivalenza”.
“È vero. In un delirio di onnipotenza avevi anche raccontato la parabola dei Lego, per spiegare il concetto di classe di equivalenza”.
“Perfetto. Ora facciamo la stessa cosa: definiamo numero ordinale una classe di equivalenza di una relazione molto simile a quella usata per i numeri cardinali”.
“Allora avevamo detto che due insiemi erano in relazione se esiste una corrispondenza biunivoca tra loro”.
“Giusto. Ora modifichiamo la relazione leggermente: due insiemi bene ordinati sono in relazione se esiste una corrispondenza biunivoca che conserva l'ordine tra loro”.
“Ah. Quindi abbiamo una informazione in più, l'ordinamento tra gli elementi di un insieme. Anzi, ne avremmo due in più: gli insiemi devono essere anche bene ordinati”.
“Sì, ma ammettendo l'assioma della scelta, tutti lo sono”.
“E quindi, ora abbiamo preso gli insiemi bene ordinati e li abbiamo raggruppati secondo il loro ordinamento?”.
“No, li abbiamo raggruppati secondo la loro cardinalità e il loro ordinamento”.
“Ah, già, devono avere la stessa cardinalità, perché comunque abbiamo una funzione biunivoca tra uno e l'altro”.
“Esattamente. Ora, ogni classe di equivalenza contiene infiniti insiemi: sarebbe bene trovare un modo per scegliere, in maniera standard, un rappresentante”.
“E questo modo esiste?”.
“Certo, e l'abbiamo anche già visto, quando abbiamo definito i numeri naturali a partire dall'insieme vuoto”.
“Uhm, come funzionerebbe?”.
“L'insieme vuoto è il rappresentante della classe degli insiemi con zero elementi (l'unica classe che contiene solo un elemento, cioè l'insieme vuoto stesso). Insomma, di insiemi vuoti ce n'è uno solo”.
“D'accordo”.
“Diciamo allora che l'insieme vuoto è l'ordinale che chiamiamo zero: {} = 0”.
“Ah, ora ricordo qualcosa”.
“Il secondo ordinale, quello che corrisponde agli insiemi con un elemento, è l'insieme che contiene l'insieme vuoto, cioè l'insieme che contiene lo zero. Lo chiamiamo 1: {{}} = {0} = 1”.
“Ho capito. Poi indichiamo con 2 l'insieme che contiene 0 e 1: {0,1} = 2”.
“Sì, volendo espandere tutti i simboli dovremmo scrivere {{},{{}}} = {0,{0}} = {0,1} = 2”.
“Va bene, ho capito. In pratica ogni nuovo numero è l'insieme di tutti i vecchi numeri”.
“Giustissimo, è proprio così”.
“Ma quindi tutti i numeri naturali sono ordinali?”.
“Già”.
“E sono anche cardinali, però”.
“Vero”.
“Quindi, se non c'è differenza tra ordinali e cardinali, perché li abbiamo definiti?”.
“Perché la differenza ci sarà, ma più avanti”.
“Quanto più avanti?”.
“Tanto”.
La cardinalità, abbiamo visto, è una proprietà degli insiemi. Con i numeri ordinali, invece, vogliamo tenere conto anche delle relazioni d'ordine che sono definite sugli insiemi che stiamo considerando.
È necessaria, ed importante, una prima definizione: un insieme si dice bene ordinato se ogni suo sottoinsieme ammette un primo elemento.
“Cominciamo con gli esempi?”.
“Ok. Prendi l'insieme dei numeri naturali, con l'ordinamento usuale”.
“Bene. Poi?”.
“Poi prendi un qualunque suo sottoinsieme, finito o infinito, non importa”.
“Ok. Prendiamo {42,272,314}”.
“Domanda: è vero che ammette un primo elemento? Cioè, è vero che ha minimo?”.
“Certo: 42”.
“Ed è vero che questa proprietà è valida per ogni sottoinsieme, anche se infinito?”.
“Direi di sì, se è infinito contiene elementi sempre più grandi, ma un minimo c'è”.
“Perfetto. Quindi diciamo che l'insieme dei numeri naturali, dotato dell'ordinamento usuale, è bene ordinato”.
“Ok. E se cambio insieme?”.
“Se ricordi, ne avevamo già parlato. Se ammettiamo come vero l'assioma della scelta, ogni insieme è bene ordinabile”.
“Mh, è vero. Avevi anche detto che nessuno è riuscito a trovare un buon ordinamento per i numeri reali”.
“Esatto”.
“Però nemmeno i numeri interi sono bene ordinabili. Se prendo un insieme che contiene infiniti numeri negativi, questo non ha minimo”.
“Vero, ma questo non significa che gli interi non sono bene ordinabili, ma solo che l'ordinamento che stai considerando non è un buon ordinamento”.
“In che senso? Potrei cambiarlo?”.
“Certo. Prova a considerare questo nuovo ordinamento degli interi: {0,1,-1,2,-2,3,-3,...}”.
“Ah! Vedo, questo è un buon ordinamento, a sinistra mi fermo”.
“Perfetto. Ora facciamo un passo avanti. Ricordi le funzioni biunivoche?”.
“Certo, allora la matematica mi sembrava più semplice”.
“Bene, quando parliamo di insiemi ordinati, potremmo desiderare che una funzione biunivoca tra due insiemi preservi l'ordine”.
“Uhm, servirebbe un altro esempio”.
“Prendiamo due insiemi ordinati, per esempio {1,2,3} e {Qua, Paperino, Paperone}”.
“Ehm, capisco l'ordinamento del primo insieme, ma non capisco bene quello del secondo...”.
“Diciamo che è quello dell'età. I tre personaggi sono ordinati in base alla loro età”.
“Va bene. Secondo quanto ho imparato, sono due insiemi di cardinalità 3, ed esiste una corrispondenza biunivoca tra uno e l'altro”.
“Ottimo. Ora ti propongo questa corrispondenza:”.
1 - Qua 2 - Paperone 3 - Paperino
“Certamente è biunivoca”.
“Infatti. Però non preserva l'ordine. Puoi vedere che 2 è minore di 3, ma f(2), cioè Paperone, non è minore di f(3), cioè Paperino”.
“Ho capito, ora è chiaro. Se vuoi fare una corrispondenza biunivoca che conserva l'ordine devi scrivere questo:”.
1 - Qua 2 - Paperino 3 - Paperone
“Bene. Ora, se ricordi, avevamo definito i numeri cardinali con le relazioni di equivalenza”.
“È vero. In un delirio di onnipotenza avevi anche raccontato la parabola dei Lego, per spiegare il concetto di classe di equivalenza”.
“Perfetto. Ora facciamo la stessa cosa: definiamo numero ordinale una classe di equivalenza di una relazione molto simile a quella usata per i numeri cardinali”.
“Allora avevamo detto che due insiemi erano in relazione se esiste una corrispondenza biunivoca tra loro”.
“Giusto. Ora modifichiamo la relazione leggermente: due insiemi bene ordinati sono in relazione se esiste una corrispondenza biunivoca che conserva l'ordine tra loro”.
“Ah. Quindi abbiamo una informazione in più, l'ordinamento tra gli elementi di un insieme. Anzi, ne avremmo due in più: gli insiemi devono essere anche bene ordinati”.
“Sì, ma ammettendo l'assioma della scelta, tutti lo sono”.
“E quindi, ora abbiamo preso gli insiemi bene ordinati e li abbiamo raggruppati secondo il loro ordinamento?”.
“No, li abbiamo raggruppati secondo la loro cardinalità e il loro ordinamento”.
“Ah, già, devono avere la stessa cardinalità, perché comunque abbiamo una funzione biunivoca tra uno e l'altro”.
“Esattamente. Ora, ogni classe di equivalenza contiene infiniti insiemi: sarebbe bene trovare un modo per scegliere, in maniera standard, un rappresentante”.
“E questo modo esiste?”.
“Certo, e l'abbiamo anche già visto, quando abbiamo definito i numeri naturali a partire dall'insieme vuoto”.
“Uhm, come funzionerebbe?”.
“L'insieme vuoto è il rappresentante della classe degli insiemi con zero elementi (l'unica classe che contiene solo un elemento, cioè l'insieme vuoto stesso). Insomma, di insiemi vuoti ce n'è uno solo”.
“D'accordo”.
“Diciamo allora che l'insieme vuoto è l'ordinale che chiamiamo zero: {} = 0”.
“Ah, ora ricordo qualcosa”.
“Il secondo ordinale, quello che corrisponde agli insiemi con un elemento, è l'insieme che contiene l'insieme vuoto, cioè l'insieme che contiene lo zero. Lo chiamiamo 1: {{}} = {0} = 1”.
“Ho capito. Poi indichiamo con 2 l'insieme che contiene 0 e 1: {0,1} = 2”.
“Sì, volendo espandere tutti i simboli dovremmo scrivere {{},{{}}} = {0,{0}} = {0,1} = 2”.
“Va bene, ho capito. In pratica ogni nuovo numero è l'insieme di tutti i vecchi numeri”.
“Giustissimo, è proprio così”.
“Ma quindi tutti i numeri naturali sono ordinali?”.
“Già”.
“E sono anche cardinali, però”.
“Vero”.
“Quindi, se non c'è differenza tra ordinali e cardinali, perché li abbiamo definiti?”.
“Perché la differenza ci sarà, ma più avanti”.
“Quanto più avanti?”.
“Tanto”.
domenica 28 settembre 2008
Outing
Ho cambiato la mia firma, visto che in altre parti del mondo mi firmo zar e che lo pseudonimo anonimo che mi ero scelto aveva lo scopo di non farmi riconoscere dai miei studenti — riconoscimento che è prontamente avvenuto dopo pochi mesi di post...
sabato 27 settembre 2008
Verso l'infinito, ma con calma - l'ipotesi del continuo
Esistono insiemi più infiniti dei numeri naturali e meno infiniti dei numeri reali? Usando termini un po' più rigorosi, esistono cardinali maggiori di ℵ0 e minori di 2ℵ0? Cantor era convinto che la risposta fosse no, ma non riuscì a dimostrare questa sua affermazione, che diventò nota con il nome di ipotesi del continuo.
Il giorno 8 agosto 1900 il matematico David Hilbert tenne una conferenza al congresso internazionale dei matematici, svoltasi quell'anno a Parigi. In quel suo discorso di inizio secolo, Hilbert propose alla comunità matematica una lista di problemi che riteneva fondamentali.
Il primo della lista era l'ipotesi del continuo.
“E dopo tutto questo tempo è stato risolto?”.
“Ecco, non esattamente”.
“Quindi non si sa ancora se l'ipotesi del continuo è vera oppure no?”.
“No, no, si sa tutto, ma la risposta non risolve il problema”.
“Come è possibile?”.
“Il primo ad occuparsi della dimostrazione fu Kurt Gödel, che nel 1940 riuscì a dimostrare che non si può dimostrare che l'ipotesi del continuo sia falsa”.
“Oh povero me. Ha dimostrato che non si può fare una dimostrazione?”.
“Sì, Gödel era un maestro della metamatematica”.
“Mamma mia. Quindi se non si può dimostrare che è falsa, sarà vera?”.
“Eh, no. Il fatto che non si possa dimostrare che l'ipotesi del continuo sia falsa significa che gli assiomi della teoria degli insiemi sono compatibili con essa. Immaginare che sia vera non produce contraddizioni, ma ancora non abbiamo dimostrato che lo è davvero”.
“Va bene. Ma visto che una affermazione può essere vera o falsa, se non è falsa allora è vera”.
“Ecco, il fatto è che nel 1963 Paul Cohen dimostrò che non si può dimostrare nemmeno che l'ipotesi del continuo sia vera”.
“Eh?”.
“Sì, hai capito bene. Se immagini che sia vera, non hai contraddizioni. Se immagini che sia falsa, non hai contraddizioni”.
“Quindi può essere sia vera che falsa? Non ha senso!”.
“Invece un senso c'è. Queste due dimostrazioni fanno vedere che l'ipotesi del continuo è indecidibile, cioè gli assiomi non sono sufficienti per dimostrarla o per negarla”.
“E quindi gli assiomi sono incompleti?”.
“Esattamente. Puoi farti una teoria degli insiemi in cui l'ipotesi del continuo è vera, e un'altra teoria in cui è falsa. Tutte e due stanno in piedi”.
“Ma ce ne sarà una più giusta dell'altra”.
“Questa volta sono io che mi avvalgo della facoltà di non rispondere”.
“Perché?”.
“Cantor pensava che fosse vera, provò a dimostrarla ma non ci riuscì. Gödel era convinto che fosse falsa, invece”.
“E però avevano ragione tutti e due”.
“Sì, ma Gödel era una testa dura, e pensava che l'impossibilità di dimostrare la sua tesi fosse colpa soltanto del sistema di assiomi, che non era stato scelto in modo corretto”.
“Bella forza! Modifichi le regole e poi dimostri quello che vuoi”.
“Bè, non puoi proprio dimostrare quello che vuoi, perché le regole devono essere comunque consistenti. Comunque Gödel credeva nell'esistenza degli oggetti matematici in modo indipendente dalla loro dimostrazione. Insomma, l'ipotesi del continuo per lui era falsa perché secondo lui la matematica è fatta così. Se non è riuscito a dimostrarlo vuol dire che non ha usato gli strumenti giusti per osservare una realtà che comunque è lì ed esiste, prima ancora che tu la scopra”.
“Wow, ma questa è matematica o teologia?”.
“C'è chi dice che, a questi livelli, non ci sia molta differenza”.
“Comincio a rendermene conto...”.
“C'è una frase emblematica a riguardo, pronunciata da Hilbert. Dice: Nessuno potrà cacciarci dal Paradiso che Cantor ha creato”.
“Bella”.
“Nello stesso periodo Leopold Kronecker, un matematico al quale non piacevano le idee di Cantor, pronunciò questa: Dio fece i numeri naturali; tutto il resto è opera dell'uomo”.
“Ah, ma litigavano pure?”.
“Eh sì. E, per concludere, ti ricordi dell'insieme di tutti gli insiemi?”.
“Quello innominabile?”.
“Quello. Cantor lo chiamava Infinito Assoluto”.
“E allora?”.
“Bé, per lui l'Infinito Assoluto era Dio”.
Il giorno 8 agosto 1900 il matematico David Hilbert tenne una conferenza al congresso internazionale dei matematici, svoltasi quell'anno a Parigi. In quel suo discorso di inizio secolo, Hilbert propose alla comunità matematica una lista di problemi che riteneva fondamentali.
Il primo della lista era l'ipotesi del continuo.
“E dopo tutto questo tempo è stato risolto?”.
“Ecco, non esattamente”.
“Quindi non si sa ancora se l'ipotesi del continuo è vera oppure no?”.
“No, no, si sa tutto, ma la risposta non risolve il problema”.
“Come è possibile?”.
“Il primo ad occuparsi della dimostrazione fu Kurt Gödel, che nel 1940 riuscì a dimostrare che non si può dimostrare che l'ipotesi del continuo sia falsa”.
“Oh povero me. Ha dimostrato che non si può fare una dimostrazione?”.
“Sì, Gödel era un maestro della metamatematica”.
“Mamma mia. Quindi se non si può dimostrare che è falsa, sarà vera?”.
“Eh, no. Il fatto che non si possa dimostrare che l'ipotesi del continuo sia falsa significa che gli assiomi della teoria degli insiemi sono compatibili con essa. Immaginare che sia vera non produce contraddizioni, ma ancora non abbiamo dimostrato che lo è davvero”.
“Va bene. Ma visto che una affermazione può essere vera o falsa, se non è falsa allora è vera”.
“Ecco, il fatto è che nel 1963 Paul Cohen dimostrò che non si può dimostrare nemmeno che l'ipotesi del continuo sia vera”.
“Eh?”.
“Sì, hai capito bene. Se immagini che sia vera, non hai contraddizioni. Se immagini che sia falsa, non hai contraddizioni”.
“Quindi può essere sia vera che falsa? Non ha senso!”.
“Invece un senso c'è. Queste due dimostrazioni fanno vedere che l'ipotesi del continuo è indecidibile, cioè gli assiomi non sono sufficienti per dimostrarla o per negarla”.
“E quindi gli assiomi sono incompleti?”.
“Esattamente. Puoi farti una teoria degli insiemi in cui l'ipotesi del continuo è vera, e un'altra teoria in cui è falsa. Tutte e due stanno in piedi”.
“Ma ce ne sarà una più giusta dell'altra”.
“Questa volta sono io che mi avvalgo della facoltà di non rispondere”.
“Perché?”.
“Cantor pensava che fosse vera, provò a dimostrarla ma non ci riuscì. Gödel era convinto che fosse falsa, invece”.
“E però avevano ragione tutti e due”.
“Sì, ma Gödel era una testa dura, e pensava che l'impossibilità di dimostrare la sua tesi fosse colpa soltanto del sistema di assiomi, che non era stato scelto in modo corretto”.
“Bella forza! Modifichi le regole e poi dimostri quello che vuoi”.
“Bè, non puoi proprio dimostrare quello che vuoi, perché le regole devono essere comunque consistenti. Comunque Gödel credeva nell'esistenza degli oggetti matematici in modo indipendente dalla loro dimostrazione. Insomma, l'ipotesi del continuo per lui era falsa perché secondo lui la matematica è fatta così. Se non è riuscito a dimostrarlo vuol dire che non ha usato gli strumenti giusti per osservare una realtà che comunque è lì ed esiste, prima ancora che tu la scopra”.
“Wow, ma questa è matematica o teologia?”.
“C'è chi dice che, a questi livelli, non ci sia molta differenza”.
“Comincio a rendermene conto...”.
“C'è una frase emblematica a riguardo, pronunciata da Hilbert. Dice: Nessuno potrà cacciarci dal Paradiso che Cantor ha creato”.
“Bella”.
“Nello stesso periodo Leopold Kronecker, un matematico al quale non piacevano le idee di Cantor, pronunciò questa: Dio fece i numeri naturali; tutto il resto è opera dell'uomo”.
“Ah, ma litigavano pure?”.
“Eh sì. E, per concludere, ti ricordi dell'insieme di tutti gli insiemi?”.
“Quello innominabile?”.
“Quello. Cantor lo chiamava Infinito Assoluto”.
“E allora?”.
“Bé, per lui l'Infinito Assoluto era Dio”.
venerdì 26 settembre 2008
Si fa presto a dire cina /3
Dopo le classifiche basate sul rapporto medaglie/abitanti, ecco un altro argomento su cui meditare. Come stabilire l'ordinamento in classifica dei vari stati? Perché, ad esempio, dieci medaglie d'oro e una d'argento dovrebbero essere meglio di nove medaglie d'oro e cinquanta d'argento? Come sarebbe meglio ordinare le terne di medaglie?
Si potrebbe privilegiare il totale delle medaglie, e usare le medaglie d'oro per gli spareggi (in questo caso, 9 ori e 50 argenti sono meglio di 10 ori e 1 argento). Oppure si potrebbero privilegiare gli ori, usando gli argenti e i bronzi come spareggio. Esistono anche altri sistemi intermedi tra questi due: si può assegnare un punteggio alle medaglie d'oro, un secondo punteggio più basso del primo agli argenti, e un terzo ancora minore ai bronzi. Per esempio, si potrebbe stabilire che ogni medaglia d'oro vale 3 punti, ogni argento 2 e ogni bronzo 1.
Un vero matematico, a dir la verità, preferirebbe proporre un punteggio pari, ad esempio, a π2 per l'oro, π per l'argento e 1 per il bronzo, in modo da non avere parità se non nel caso in cui due stati riescano ad ottenere esattamente le stesse medaglie.
Questi diversi sistemi producono, purtroppo, classifiche diverse. È possibile stilare una classifica che metta tutti d'accordo?
In questa pagina viene proposto un nuovo tipo di ordinamento, che idealmente potrebbe essere condiviso da tutti, e che si basa sulle seguenti leggi:
Diciamo allora che uno stato A è stato migliore di un altro stato B se il medagliere di B può essere trasformato nel medagliere di A mediante una sequenza di aggiunte di medaglie oppure di sostituzione di medaglie basse con medaglie alte.
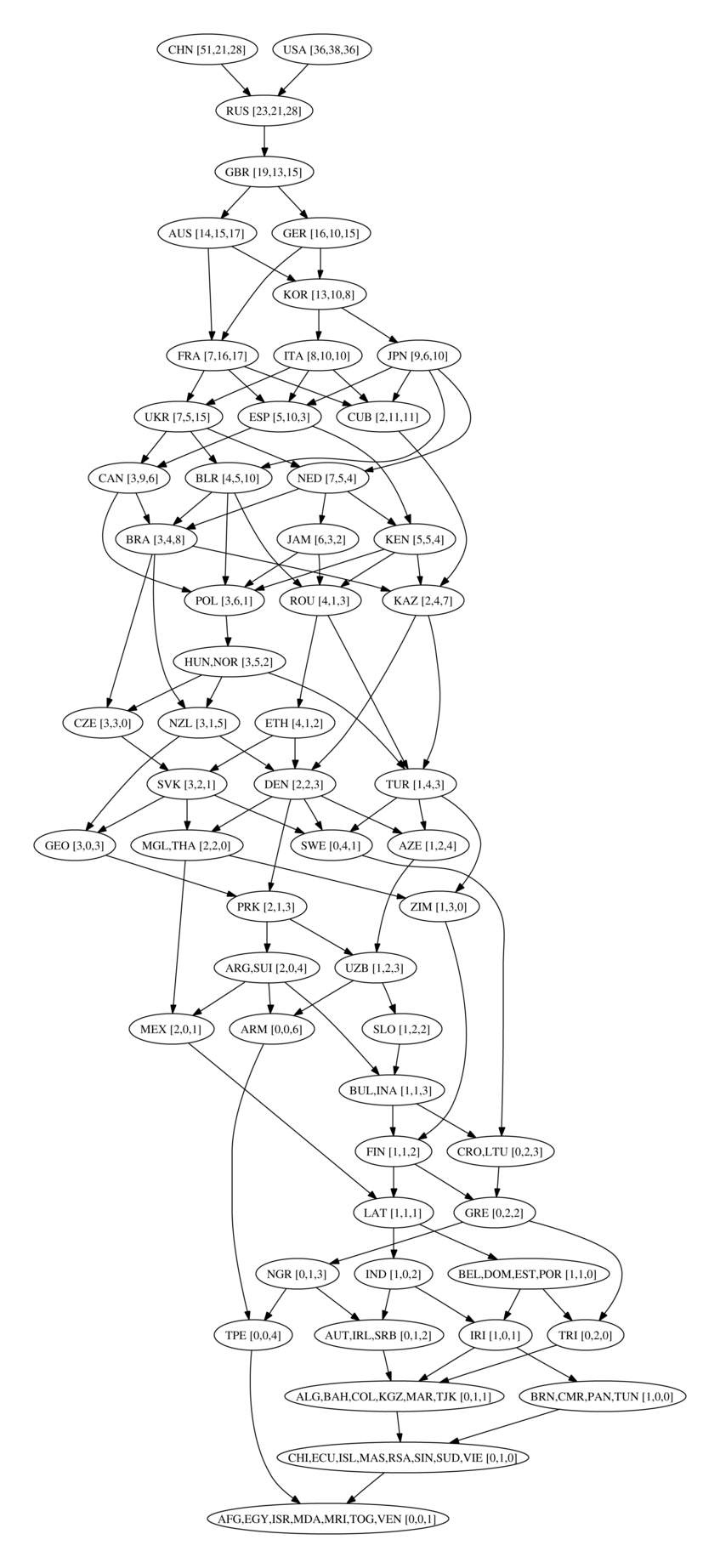
Per esempio, indicando con una terna di numeri le medaglie ottenute, ordinando dall'oro al bronzo, l'Inghilterra ha ottenuto (19,13,15), mentre l'Austria (14,15,17). Sostituiamo 2 medaglie di bronzo dell'Austria con 2 d'argento, ottenendo (14,17,15). Ora sostituiamo 4 argenti con altrettanti ori, arrivando a (18,13,15). Ora dobbiamo aggiungere un oro per arrivare a (19,13,15), quindi l'Austria ha fatto peggio dell'Inghilterra.
Quello che abbiamo ottenuto è un ordinamento parziale: non è detto che due medaglieri siano sempre confrontabili. Per esempio, non lo sono Cina (51,21,28) e Stati Uniti (36,38,36). Ma l'ordinamento che si ottiene dovrebbe mettere d'accordo tutti.
Questo è il risultato:
Si potrebbe privilegiare il totale delle medaglie, e usare le medaglie d'oro per gli spareggi (in questo caso, 9 ori e 50 argenti sono meglio di 10 ori e 1 argento). Oppure si potrebbero privilegiare gli ori, usando gli argenti e i bronzi come spareggio. Esistono anche altri sistemi intermedi tra questi due: si può assegnare un punteggio alle medaglie d'oro, un secondo punteggio più basso del primo agli argenti, e un terzo ancora minore ai bronzi. Per esempio, si potrebbe stabilire che ogni medaglia d'oro vale 3 punti, ogni argento 2 e ogni bronzo 1.
Un vero matematico, a dir la verità, preferirebbe proporre un punteggio pari, ad esempio, a π2 per l'oro, π per l'argento e 1 per il bronzo, in modo da non avere parità se non nel caso in cui due stati riescano ad ottenere esattamente le stesse medaglie.
Questi diversi sistemi producono, purtroppo, classifiche diverse. È possibile stilare una classifica che metta tutti d'accordo?
In questa pagina viene proposto un nuovo tipo di ordinamento, che idealmente potrebbe essere condiviso da tutti, e che si basa sulle seguenti leggi:
- il numero di medaglie conta, a parità di altri fattori: se uno stato A ha ottenuto almeno tanti ori, almeno tanti argenti e almeno tanti bronzi di quanti ne abbia ottenuto uno stato B, allora i due stati sono almeno pari in classifica,
- oro è meglio di argento, argento è meglio di bronzo: se lo stato A ha ottenuto un argento in più e un bronzo in meno dello stato B, allora deve essere più in alto in classifica. Infatti B, per ottenere lo stesso risultato di A, dovrebbe fare meglio in una specialità in cui ha vinto il bronzo e riuscire a ottenere l'argento.
Diciamo allora che uno stato A è stato migliore di un altro stato B se il medagliere di B può essere trasformato nel medagliere di A mediante una sequenza di aggiunte di medaglie oppure di sostituzione di medaglie basse con medaglie alte.
Per esempio, indicando con una terna di numeri le medaglie ottenute, ordinando dall'oro al bronzo, l'Inghilterra ha ottenuto (19,13,15), mentre l'Austria (14,15,17). Sostituiamo 2 medaglie di bronzo dell'Austria con 2 d'argento, ottenendo (14,17,15). Ora sostituiamo 4 argenti con altrettanti ori, arrivando a (18,13,15). Ora dobbiamo aggiungere un oro per arrivare a (19,13,15), quindi l'Austria ha fatto peggio dell'Inghilterra.
Quello che abbiamo ottenuto è un ordinamento parziale: non è detto che due medaglieri siano sempre confrontabili. Per esempio, non lo sono Cina (51,21,28) e Stati Uniti (36,38,36). Ma l'ordinamento che si ottiene dovrebbe mettere d'accordo tutti.
Questo è il risultato:
Verso l'infinito, ma con calma - le dimensioni non contano
Abbiamo chiamato con c (c gotico) la cardinalità dell'insieme dei numeri reali, e abbiamo visto che è maggiore di quella dei numeri naturali. Dato che i numeri reali sono in corrispondenza biunivoca con i punti di una retta, che ha dimensione uguale a 1, si potrebbe pensare che la cardinalità del piano sia maggiore di c, visto che il piano ha dimensione 2. E invece no.
“Puoi naturalmente dimostrare questa affermazione, vero?”.
“Certo”.
“E sarà una cosa complicatissima”.
“No, questa è facile. Per prima cosa, invece di confrontare la retta con il piano, confrontiamo il segmento [0,1) con il quadrato [0,1)×[0,1)”.
“Quello sarebbe un quadrato?”.
“I Veri Matematici lo chiamano prodotto cartesiano, ma è semplice: è l'insieme delle coppie i cui elementi appartengono a [0,1). In pratica è un quadrato, i cui punti hanno coordinate comprese tra 0 e 1, 0 incluso e 1 no”.
“Va bene. Ora costruirai una corrispondenza biunivoca tra il segmento e il quadrato?”.
“No, prima costruisco una funzione iniettiva che immerge il segmento nel quadrato, poi un'altra funzione iniettiva che immerge il quadrato nel segmento”.
“Ok. Il primo caso è semplice, non è difficile immergere un segmento in un quadrato”.
“Bene, come faresti?”.
“Ad ogni punto del segmento associo un punto sulla base del quadrato, per esempio”.
“Bravo. A x associ (x,0), ed è fatta. La funzione è iniettiva, a due x diversi corrispondono due coppie diverse”.
“Sì. Non riesco invece a immaginare come fare per l'operazione contraria”.
“Si fa così: prendi un punto del quadrato, e indicalo con (x,y)”.
“Bene, sia x che y sono compresi tra 0 e 1, 0 incluso e 1 no”.
“Ora scrivili sotto forma di numeri decimali, così:”.
x = 0.x1x2x3...
y = 0.y1y2y3...
“Uhm, e se i numeri sono decimali finiti?”.
“Vorrà dire che da un certo punto in poi la successione delle cifre decimali sarà sempre uguale a 0”.
“Va bene. Accettiamo il periodo 9?”.
“No, quello no”.
“Ci sono. Ora che facciamo?”.
“Ora costruiamo questo numero: 0.x1y1x2y2x3y3...”.
“Alterni le cifre decimali?”.
“Già. Hai visto che abbiamo ottenuto un punto del segmento [0,1)?”.
“Vedo. Mi pare di aver capito, però, che la funzione debba essere iniettiva, altrimenti non funziona”.
“Giusto. Hai capito perché non funziona?”.
“Perché se non uso una funzione iniettiva, potrei far corrispondere a tutti i punti del quadrato anche un solo punto, chessò, 42”.
“Bravo. La funzione f(x,y) = 42 comprime il quadrato in un punto, ma non è iniettiva e non può essere usata per i calcoli di cardinalità, naturalmente”.
“Ho capito. E questa funzione che alterna le cifre decimali è iniettiva?”.
“Sì, perché se prendi due punti diversi nel piano questi differiranno in almeno una coordinata, e quindi almeno una delle due espansioni decimali cambierà”.
“Ah, giusto, e allora cambierà anche il numero che otterrai alternando le cifre decimali. Quindi la tua funzione è iniettiva dal quadrato al segmento”.
“Sì, addirittura qualche punto del segmento viene lasciato fuori”.
“Uh? Quali punti?”.
“Per esempio, il punto che corrisponde a 0.190919091909...”.
“Fammi capire, questo punto sarebbe generato da 0.101010... e da 0.999999... Ah, ho capito, avevamo detto di non considerare il periodo 9. Bè, ancora meglio, siamo riusciti a immergere il quadrato in un sottoinsieme del segmento”.
“Proprio così. Allora, applicando il teorema di Cantor-Bernstein-Schröder, possiamo dire che quadrato e segmento hanno la stessa cardinalità. E quindi anche retta e piano, naturalmente”.
“Bello. E quindi esistono solo due cardinalità, ℵ0 e c?”.
“Oh, no. Ricordati che abbiamo dimostrato che 2α è sempre maggiore di α, e dunque puoi costruire una sequenza di cardinali sempre più grandi così come abbiamo fatto quando siamo passati da ℵ0 a 2ℵ0”.
“Facendo l'insieme delle parti, quindi?”.
“Certo. Se consideri l'insieme delle parti dei numeri reali, questo avrà cardinalità 2c, cioè 22ℵ0”.
“Ah, quindi possiamo salire sempre di più, quanto vogliamo”.
“Già”.
“Un po' come contare gli infiniti con i numeri naturali”.
“Ecco...”.
“Un momento!”.
“Ahia”.
“E se non fosse come con i numeri naturali?”.
“Ahi ahi”.
“Magari c'è qualcosa in mezzo tra ℵ0 e 2ℵ0?”.
“Ohi ohi”.
“Ti sei fatto male?”.
“Puoi naturalmente dimostrare questa affermazione, vero?”.
“Certo”.
“E sarà una cosa complicatissima”.
“No, questa è facile. Per prima cosa, invece di confrontare la retta con il piano, confrontiamo il segmento [0,1) con il quadrato [0,1)×[0,1)”.
“Quello sarebbe un quadrato?”.
“I Veri Matematici lo chiamano prodotto cartesiano, ma è semplice: è l'insieme delle coppie i cui elementi appartengono a [0,1). In pratica è un quadrato, i cui punti hanno coordinate comprese tra 0 e 1, 0 incluso e 1 no”.
“Va bene. Ora costruirai una corrispondenza biunivoca tra il segmento e il quadrato?”.
“No, prima costruisco una funzione iniettiva che immerge il segmento nel quadrato, poi un'altra funzione iniettiva che immerge il quadrato nel segmento”.
“Ok. Il primo caso è semplice, non è difficile immergere un segmento in un quadrato”.
“Bene, come faresti?”.
“Ad ogni punto del segmento associo un punto sulla base del quadrato, per esempio”.
“Bravo. A x associ (x,0), ed è fatta. La funzione è iniettiva, a due x diversi corrispondono due coppie diverse”.
“Sì. Non riesco invece a immaginare come fare per l'operazione contraria”.
“Si fa così: prendi un punto del quadrato, e indicalo con (x,y)”.
“Bene, sia x che y sono compresi tra 0 e 1, 0 incluso e 1 no”.
“Ora scrivili sotto forma di numeri decimali, così:”.
x = 0.x1x2x3...
y = 0.y1y2y3...
“Uhm, e se i numeri sono decimali finiti?”.
“Vorrà dire che da un certo punto in poi la successione delle cifre decimali sarà sempre uguale a 0”.
“Va bene. Accettiamo il periodo 9?”.
“No, quello no”.
“Ci sono. Ora che facciamo?”.
“Ora costruiamo questo numero: 0.x1y1x2y2x3y3...”.
“Alterni le cifre decimali?”.
“Già. Hai visto che abbiamo ottenuto un punto del segmento [0,1)?”.
“Vedo. Mi pare di aver capito, però, che la funzione debba essere iniettiva, altrimenti non funziona”.
“Giusto. Hai capito perché non funziona?”.
“Perché se non uso una funzione iniettiva, potrei far corrispondere a tutti i punti del quadrato anche un solo punto, chessò, 42”.
“Bravo. La funzione f(x,y) = 42 comprime il quadrato in un punto, ma non è iniettiva e non può essere usata per i calcoli di cardinalità, naturalmente”.
“Ho capito. E questa funzione che alterna le cifre decimali è iniettiva?”.
“Sì, perché se prendi due punti diversi nel piano questi differiranno in almeno una coordinata, e quindi almeno una delle due espansioni decimali cambierà”.
“Ah, giusto, e allora cambierà anche il numero che otterrai alternando le cifre decimali. Quindi la tua funzione è iniettiva dal quadrato al segmento”.
“Sì, addirittura qualche punto del segmento viene lasciato fuori”.
“Uh? Quali punti?”.
“Per esempio, il punto che corrisponde a 0.190919091909...”.
“Fammi capire, questo punto sarebbe generato da 0.101010... e da 0.999999... Ah, ho capito, avevamo detto di non considerare il periodo 9. Bè, ancora meglio, siamo riusciti a immergere il quadrato in un sottoinsieme del segmento”.
“Proprio così. Allora, applicando il teorema di Cantor-Bernstein-Schröder, possiamo dire che quadrato e segmento hanno la stessa cardinalità. E quindi anche retta e piano, naturalmente”.
“Bello. E quindi esistono solo due cardinalità, ℵ0 e c?”.
“Oh, no. Ricordati che abbiamo dimostrato che 2α è sempre maggiore di α, e dunque puoi costruire una sequenza di cardinali sempre più grandi così come abbiamo fatto quando siamo passati da ℵ0 a 2ℵ0”.
“Facendo l'insieme delle parti, quindi?”.
“Certo. Se consideri l'insieme delle parti dei numeri reali, questo avrà cardinalità 2c, cioè 22ℵ0”.
“Ah, quindi possiamo salire sempre di più, quanto vogliamo”.
“Già”.
“Un po' come contare gli infiniti con i numeri naturali”.
“Ecco...”.
“Un momento!”.
“Ahia”.
“E se non fosse come con i numeri naturali?”.
“Ahi ahi”.
“Magari c'è qualcosa in mezzo tra ℵ0 e 2ℵ0?”.
“Ohi ohi”.
“Ti sei fatto male?”.
giovedì 25 settembre 2008
Verso l'infinito, ma con calma - rette e segmenti
“Cos'è 'sta roba?”.
“Una costruzione geometrica”.
“E cosa costruisce?”.
“Una corrispondenza biunivoca”.
“Cominciamo da capo?”.
“Ok. In rosso c'è il segmento AB, sul quale è stato scelto un punto a caso, P”.
“Bene, fin qua ci sono”.
“Poi ho costruito la perpendicolare al segmento AB passante per P”.
“Bene. Vedo che passa per un punto che hai chiamato E, che sta su una semicirconferenza”.
“Esatto. La semicirconferenza è costruita in modo tale da essere tangente al segmento AB nel punto medio”.
“Ok. Immagino che C sia il centro, giusto?”.
“Giusto. Dal centro parte una semiretta che passa per E e continua fino ad incontrare la retta che contiene AB”.
“E questa semiretta incontra la retta che contiene AB in D”.
“Perfetto, questa è la costruzione”.
“E la corrispondenza biunivoca qual è?”.
“Il procedimento che abbiamo appena enunciato è la corrispondenza biunivoca. Mette in corrispondenza i punti del segmento AB ai punti della retta”.
“Ah. Immagino che sia uno dei soliti paradossi dell'infinito?”.
“Già. Ogni punto del segmento può essere portato sulla semicirconferenza, e da lì sulla retta. Viceversa, ogni punto della retta può essere portato sulla semicirconferenza e, da lì, sul segmento”.
“Uhm, e per quanto riguarda i punti A e B?”.
“Niente, quelli li lasciamo da parte. La corrispondenza biunivoca è tra i punti interni a AB e la retta”.
“Ok”.
“Quindi il segmento AB e la retta, visti ora come insiemi di numeri, hanno la stessa cardinalità”.
“Ah, ok. Ho capito dove vuoi arrivare: avevi analizzato la cardinalità di [0,1), e ora vuoi dire che ha la stessa cardinalità della retta”.
“Esatto”.
“Ma [0,1) contiene lo zero, mentre nel tuo esempio gli estremi non sono contenuti”.
“Sì, è vero. Per questo dobbiamo fare qualche passaggio in più. Abbiamo appena detto che (0,1) è in corrispondenza biunivoca con i numeri reali, quindi (0,1) e R hanno la stessa cardinalità”.
“E fin qua siamo d'accordo”.
“Ora, puoi immergere facilmente (0,1) in [0,1)”.
“Sì, è ovvio, a ogni elemento di (0,1) associo sé stesso, e sono a posto. Ho costruito una funzione iniettiva, ma non suriettiva, perché nel secondo insieme lo 0 rimane fuori”.
“E altrettanto facilmente puoi immergere [0,1) nella retta”.
“Certo. Ah, ho capito. La cardinalità di (0,1) è minore o uguale di quella di [0,1), che è minore o uguale di quella della retta, che è uguale a quella di (0,1)”.
“E mettendo insieme queste disuguaglianze col teorema di Cantor-Bernstein-Schröder cosa puoi concludere?”.
“Che le cardinalità sono tutte uguali! E sono uguali al tuo famoso c gotico”.
“Esatto. Quindi, ricapitolando tutto, 2ℵ0 = c”.
“Fiuu. Finalmente ci siamo arrivati. Immagino che poi prenderai il piano, e dirai che ha cardinalità maggiore di c, poi lo spazio che avrà cardinalità ancora più grande, poi ti divertirai ad aumentare le dimensioni come fanno i Veri Matematici”.
“No”.
“No? Perché”.
“Ti mostrerò che il piano ha la stessa cardinalità della retta. E dalla dimostrazione capirai che anche lo spazio ha la stessa cardinalità, così come tutti quegli spazi a n dimensioni che non ti piacciono tanto”.
“Oh, no, ancora paradossi”.
mercoledì 24 settembre 2008
Verso l'infinito, ma con calma - facciamo ordine
Una relazione d'ordine è una relazione che gode di tre proprietà:
Se esistesse una relazione d'ordine anche tra i numeri cardinali, allora da c ≤ 2ℵ0 e 2ℵ0 ≤ c potremmo dedurre che c = 2ℵ0.
La relazione d'ordine, effettivamente, esiste, ed è definita così: Card(A) è minore o uguale di Card(B) se esiste una funzione iniettiva da A verso B.
Dimostrare la proprietà riflessiva è semplice: esiste certamente una funzione iniettiva da A verso A, è l'identità (cioè la funzione che a ogni elemento associa sé stesso. Funzione che è biunivoca, quindi certamente iniettiva).
Anche per quanto riguarda la proprietà transitiva non ci sono problemi: se esistono una funzione f iniettiva da A verso B e una g iniettiva da B verso C, ne esiste una da A direttamente verso C, basta comporre le due.
È la proprietà antisimmetrica quella che dà più problemi. Per dimostrarla immaginiamo una partita di ping pong.
“Ping pong?”.
“Lo so che si dice tennis tavolo, ma mi piaceva di più dire ping pong”.
“Vabbè, ma cosa c'entra il ping pong?”.
“Le nostre ipotesi sono queste: esiste una funzione f iniettiva da A a B, ed esiste una funzione g iniettiva da B a A”.
“Ok, e la tesi è che esiste una funzione biunivoca da A a B. Ma il ping pong?”.
“Un momento che arrivo. Immagina di prendere un elemento di A qualsiasi”.
“Bene. Lo chiamiamo a?”.
“Chiamiamolo pallina”.
“Non starai esagerando con i nomi esotici?”.
“Questa pallina viene mandata da f in B, giusto?”.
“Giusto. Volendo, potremmo anche dire che viene rimandata da g in A”.
“Perfetto, ecco la tua partita di ping pong. La pallina si trova in A, poi con f(pallina) la mandiamo in B, poi con g(f(pallina)) di nuovo in A, e così via”.
“Non cade mai questa pallina?”.
“Mai”.
“La partita allora è un po' noiosa”.
“Già. Ma invece di seguire la pallina in avanti, vediamo il suo percorso all'indietro”.
“In che senso?”.
“Nel senso che se la pallina ora si trova in A, può darsi che prima si trovasse in B”.
“Come può darsi? Certamente viene da B, no?”.
“Non è detto. Chi l'avrebbe mandata da B verso A?”.
“La funzione g”.
“Vuoi dire che ogni elemento che si trova in A proviene da qualche elemento di B tramite la funzione g?”.
“Eh, sì”.
“Quindi vuoi dire che la funzione g è suriettiva”.
“Sì. Ah, non l'abbiamo detto nelle ipotesi. Abbiamo detto solo che g è iniettiva”.
“Dunque tutti gli elementi di B sono mandati in A, ma non è detto che ogni elemento di A provenga da qualche elemento di B”.
“Ho capito. Immagino che questo valga anche per la funzione f?”.
“Certo. Tornando alla nostra pallina, e seguendo il suo percorso all'indietro, potremmo dire che è partita dall'insieme A, oppure che è partita da B, oppure che non ha avuto un punto di partenza”.
“Quest'ultimo caso non mi è chiaro”.
“Vuol dire che, andando all'indietro, potresti non trovare mai un'origine. La pallina è sempre stata in gioco. Cioè puoi sempre andare indietro nella catena di funzioni f e g”.
“Uhm, una partita eterna”.
“Non solo: una partita eterna senza inizio, mentre gli altri due tipi un inizio ce l'avevano”.
“Va bene”.
“Allora abbiamo diviso l'insieme A in tre parti: A' è l'insieme degli elementi che fanno parte di una partita senza inizio, AA è l'insieme degli elementi che fanno parte di una partita che ha avuto inizio in A, e analogamente AB è l'insieme degli elementi che fanno parte di una partita che ha avuto inizio in B”.
“Mamma mia. Credo di esserci: tre tipi di partite, tre parti di un insieme”.
“Sì. E osserva che sono tre parti che non hanno nulla in comune: un elemento può appartenere solo a una delle tre”.
“Ok, se fai parte di una partita che è iniziata in A non puoi far parte anche di una partita senza inizio o con inizio in B”.
“Bene. Ora suddividiamo allo stesso modo anche B, ottenendo i tre insiemi B', BA e BB”.
“Perfetto. Mi pare infatti che non ci sia un ruolo privilegiato tra A e B, dovrebbero essere interscambiabili”.
“Giusto. Infatti la proprietà che stiamo dimostrando, pur chiamandosi antisimmetrica, è simmetrica”.
“E non potevamo chiamarla simmetrica?”.
“No, la proprietà simmetrica è un'altra, ricordi le relazioni di equivalenza?”.
“Va bene. Ora cosa facciamo con questi insiemi divisi in tre?”.
“Ora definiamo la corrispondenza biunivoca tra i due. E lo facciamo in tre passi, uno per ogni parte in cui abbiamo diviso i due insiemi”.
“Va bene. Cominciamo da A'?”.
“Sì. Diamo anche un nome alla corrispondenza biunivoca che stiamo definendo: la chiamiamo φ. Allora, se a è un elemento di A, definiamo φ(a) = f(a)”.
“Cioè la nuova funzione biunivoca è uguale alla vecchia f, che era iniettiva?”.
“Sull'insieme A', è così. L'elemento a appartiene a una partita senza inizio, e viene mandato in B', che contiene elementi che fanno anch'essi parte di una partita senza inizio. Siccome non c'è inizio, si può sempre tornare indietro partendo da B', e quindi in questo insieme la funzione f è biunivoca”.
“Va bene, quindi un pezzo è fatto, hai definito una funzione biunivoca tra A' e B'”.
“Ora prendiamo un elemento a appartenente a AA”.
“Quindi un elemento che fa parte di una partita che ha avuto inizio in A”.
“Sì. Anche in questo caso φ(a) = f(a)”.
“Come prima?”.
“Già. Mediante f(a) lo mandiamo in B, anzi, in BA, dato che la sua partita è iniziata in A, e invertendo f possiamo riportarlo indietro. Non c'è il pericolo che da B non si possa tornare indietro, dato che le partite di tutti gli elementi che fanno parte di BA sono iniziate in A”.
“Ho capito, se da BA possiamo sempre tornare indietro, allora f è biunivoca anche qui”.
“Sì, quindi la funzione φ che stiamo definendo è biunivoca anche tra AA e BA”.
“Immagino che il problema salti fuori con AB e BB”.
“Sì, perché in questo caso da BB non è detto che si possa tornare indietro: qualche suo elemento potrebbe costituire l'inizio di una nuova partita”.
“E allora come facciamo?”.
“In questo caso ribaltiamo il problema: se prima abbiamo usato f per andare da A verso B, ora usiamo g”.
“Uhm, in che modo?”.
“Per quanto riguarda l'insieme AB, definiamo φ(a)=g-1(a)”.
“Cosa intendi con quell'esponente -1?”.
“Intendo la funzione inversa di g: se g va da B verso A, g-1 va da A verso B”.
“Ehi, però non sappiamo se g è biunivoca. Anzi, se lo fosse il teorema sarebbe già dimostrato”.
“Giustissimo, infatti non è detto che sia biunivoca. Ma tieni presente che ora stiamo ragionando solo sugli insiemi AB e BB. In questo caso calcolare g-1(a) significa prendere un elemento a di AB e tornare indietro verso BB, e questo si può sempre fare perché la partita di cui fa parte a ha avuto origine in B”.
“Ah! E quindi non c'è pericolo che a si blocchi in AB”.
“Esattamente. Se noti, c'è una simmetria in questa dimostrazione: uso f per AA e BA, uso g per AB e BB. Per A' e B' ho usato ancora f, ma avrei potuto usare indifferentemente anche g, dato che in questo caso non c'è mai pericolo di non tornare indietro”.
“Ah, bello. Comincio a capire il concetto di eleganza in matematica”.
“E alla fine abbiamo dimostrato anche la proprietà antisimmetrica”.
“Era questo il teorema dal nome altisonante di cui mi avevi parlato?”.
“Sì, si chiama teorema di Cantor-Bernstein-Schröder. Inizialmente Cantor ne aveva data una dimostrazione che faceva uso dell'assioma della scelta, e che aveva anche una tesi più forte”.
“In che senso?”.
“Nel senso che dimostrava anche qualcosa di più, e cioè che l'ordinamento tra i cardinali è totale. Significa che due cardinali sono sempre confrontabili, cosa che ora non abbiamo invece dimostrato. Sarebbe la famosa proprietà di tricotomia”.
“Che a me sembrava tanto ovvia”.
“E che invece è equivalente all'assioma della scelta. Se è ovvia quella, allora è ovvio anche il paradosso di Banach-Tarski”.
“Povero me. Penso che farò come fanno i Veri Matematici”.
“Già. A volte far finta di niente è comodo”.
- riflessiva: ogni elemento è in relazione con sé stesso, cioè a ≤ a
- antisimmetrica: se a è in relazione con b e b in relazione con a, allora a è uguale a b; in formule: se a ≤ b e b ≤ a, allora a = b
- transitiva: se a è in relazione con b e b in relazione con c, allora a è in relazione con c; in formule: se a ≤ b e b ≤ c, allora a ≤ c.
Se esistesse una relazione d'ordine anche tra i numeri cardinali, allora da c ≤ 2ℵ0 e 2ℵ0 ≤ c potremmo dedurre che c = 2ℵ0.
La relazione d'ordine, effettivamente, esiste, ed è definita così: Card(A) è minore o uguale di Card(B) se esiste una funzione iniettiva da A verso B.
Dimostrare la proprietà riflessiva è semplice: esiste certamente una funzione iniettiva da A verso A, è l'identità (cioè la funzione che a ogni elemento associa sé stesso. Funzione che è biunivoca, quindi certamente iniettiva).
Anche per quanto riguarda la proprietà transitiva non ci sono problemi: se esistono una funzione f iniettiva da A verso B e una g iniettiva da B verso C, ne esiste una da A direttamente verso C, basta comporre le due.
È la proprietà antisimmetrica quella che dà più problemi. Per dimostrarla immaginiamo una partita di ping pong.
“Ping pong?”.
“Lo so che si dice tennis tavolo, ma mi piaceva di più dire ping pong”.
“Vabbè, ma cosa c'entra il ping pong?”.
“Le nostre ipotesi sono queste: esiste una funzione f iniettiva da A a B, ed esiste una funzione g iniettiva da B a A”.
“Ok, e la tesi è che esiste una funzione biunivoca da A a B. Ma il ping pong?”.
“Un momento che arrivo. Immagina di prendere un elemento di A qualsiasi”.
“Bene. Lo chiamiamo a?”.
“Chiamiamolo pallina”.
“Non starai esagerando con i nomi esotici?”.
“Questa pallina viene mandata da f in B, giusto?”.
“Giusto. Volendo, potremmo anche dire che viene rimandata da g in A”.
“Perfetto, ecco la tua partita di ping pong. La pallina si trova in A, poi con f(pallina) la mandiamo in B, poi con g(f(pallina)) di nuovo in A, e così via”.
“Non cade mai questa pallina?”.
“Mai”.
“La partita allora è un po' noiosa”.
“Già. Ma invece di seguire la pallina in avanti, vediamo il suo percorso all'indietro”.
“In che senso?”.
“Nel senso che se la pallina ora si trova in A, può darsi che prima si trovasse in B”.
“Come può darsi? Certamente viene da B, no?”.
“Non è detto. Chi l'avrebbe mandata da B verso A?”.
“La funzione g”.
“Vuoi dire che ogni elemento che si trova in A proviene da qualche elemento di B tramite la funzione g?”.
“Eh, sì”.
“Quindi vuoi dire che la funzione g è suriettiva”.
“Sì. Ah, non l'abbiamo detto nelle ipotesi. Abbiamo detto solo che g è iniettiva”.
“Dunque tutti gli elementi di B sono mandati in A, ma non è detto che ogni elemento di A provenga da qualche elemento di B”.
“Ho capito. Immagino che questo valga anche per la funzione f?”.
“Certo. Tornando alla nostra pallina, e seguendo il suo percorso all'indietro, potremmo dire che è partita dall'insieme A, oppure che è partita da B, oppure che non ha avuto un punto di partenza”.
“Quest'ultimo caso non mi è chiaro”.
“Vuol dire che, andando all'indietro, potresti non trovare mai un'origine. La pallina è sempre stata in gioco. Cioè puoi sempre andare indietro nella catena di funzioni f e g”.
“Uhm, una partita eterna”.
“Non solo: una partita eterna senza inizio, mentre gli altri due tipi un inizio ce l'avevano”.
“Va bene”.
“Allora abbiamo diviso l'insieme A in tre parti: A' è l'insieme degli elementi che fanno parte di una partita senza inizio, AA è l'insieme degli elementi che fanno parte di una partita che ha avuto inizio in A, e analogamente AB è l'insieme degli elementi che fanno parte di una partita che ha avuto inizio in B”.
“Mamma mia. Credo di esserci: tre tipi di partite, tre parti di un insieme”.
“Sì. E osserva che sono tre parti che non hanno nulla in comune: un elemento può appartenere solo a una delle tre”.
“Ok, se fai parte di una partita che è iniziata in A non puoi far parte anche di una partita senza inizio o con inizio in B”.
“Bene. Ora suddividiamo allo stesso modo anche B, ottenendo i tre insiemi B', BA e BB”.
“Perfetto. Mi pare infatti che non ci sia un ruolo privilegiato tra A e B, dovrebbero essere interscambiabili”.
“Giusto. Infatti la proprietà che stiamo dimostrando, pur chiamandosi antisimmetrica, è simmetrica”.
“E non potevamo chiamarla simmetrica?”.
“No, la proprietà simmetrica è un'altra, ricordi le relazioni di equivalenza?”.
“Va bene. Ora cosa facciamo con questi insiemi divisi in tre?”.
“Ora definiamo la corrispondenza biunivoca tra i due. E lo facciamo in tre passi, uno per ogni parte in cui abbiamo diviso i due insiemi”.
“Va bene. Cominciamo da A'?”.
“Sì. Diamo anche un nome alla corrispondenza biunivoca che stiamo definendo: la chiamiamo φ. Allora, se a è un elemento di A, definiamo φ(a) = f(a)”.
“Cioè la nuova funzione biunivoca è uguale alla vecchia f, che era iniettiva?”.
“Sull'insieme A', è così. L'elemento a appartiene a una partita senza inizio, e viene mandato in B', che contiene elementi che fanno anch'essi parte di una partita senza inizio. Siccome non c'è inizio, si può sempre tornare indietro partendo da B', e quindi in questo insieme la funzione f è biunivoca”.
“Va bene, quindi un pezzo è fatto, hai definito una funzione biunivoca tra A' e B'”.
“Ora prendiamo un elemento a appartenente a AA”.
“Quindi un elemento che fa parte di una partita che ha avuto inizio in A”.
“Sì. Anche in questo caso φ(a) = f(a)”.
“Come prima?”.
“Già. Mediante f(a) lo mandiamo in B, anzi, in BA, dato che la sua partita è iniziata in A, e invertendo f possiamo riportarlo indietro. Non c'è il pericolo che da B non si possa tornare indietro, dato che le partite di tutti gli elementi che fanno parte di BA sono iniziate in A”.
“Ho capito, se da BA possiamo sempre tornare indietro, allora f è biunivoca anche qui”.
“Sì, quindi la funzione φ che stiamo definendo è biunivoca anche tra AA e BA”.
“Immagino che il problema salti fuori con AB e BB”.
“Sì, perché in questo caso da BB non è detto che si possa tornare indietro: qualche suo elemento potrebbe costituire l'inizio di una nuova partita”.
“E allora come facciamo?”.
“In questo caso ribaltiamo il problema: se prima abbiamo usato f per andare da A verso B, ora usiamo g”.
“Uhm, in che modo?”.
“Per quanto riguarda l'insieme AB, definiamo φ(a)=g-1(a)”.
“Cosa intendi con quell'esponente -1?”.
“Intendo la funzione inversa di g: se g va da B verso A, g-1 va da A verso B”.
“Ehi, però non sappiamo se g è biunivoca. Anzi, se lo fosse il teorema sarebbe già dimostrato”.
“Giustissimo, infatti non è detto che sia biunivoca. Ma tieni presente che ora stiamo ragionando solo sugli insiemi AB e BB. In questo caso calcolare g-1(a) significa prendere un elemento a di AB e tornare indietro verso BB, e questo si può sempre fare perché la partita di cui fa parte a ha avuto origine in B”.
“Ah! E quindi non c'è pericolo che a si blocchi in AB”.
“Esattamente. Se noti, c'è una simmetria in questa dimostrazione: uso f per AA e BA, uso g per AB e BB. Per A' e B' ho usato ancora f, ma avrei potuto usare indifferentemente anche g, dato che in questo caso non c'è mai pericolo di non tornare indietro”.
“Ah, bello. Comincio a capire il concetto di eleganza in matematica”.
“E alla fine abbiamo dimostrato anche la proprietà antisimmetrica”.
“Era questo il teorema dal nome altisonante di cui mi avevi parlato?”.
“Sì, si chiama teorema di Cantor-Bernstein-Schröder. Inizialmente Cantor ne aveva data una dimostrazione che faceva uso dell'assioma della scelta, e che aveva anche una tesi più forte”.
“In che senso?”.
“Nel senso che dimostrava anche qualcosa di più, e cioè che l'ordinamento tra i cardinali è totale. Significa che due cardinali sono sempre confrontabili, cosa che ora non abbiamo invece dimostrato. Sarebbe la famosa proprietà di tricotomia”.
“Che a me sembrava tanto ovvia”.
“E che invece è equivalente all'assioma della scelta. Se è ovvia quella, allora è ovvio anche il paradosso di Banach-Tarski”.
“Povero me. Penso che farò come fanno i Veri Matematici”.
“Già. A volte far finta di niente è comodo”.
martedì 23 settembre 2008
Queste son gite
Sono appena tornato da una gita (non si devono chiamare gite, ma visite d'istruzione (ed è bene tenere l'apostrofo, che la confusione con distruzione potrebbe non essere fuorviante)) alla stazione di osservazione climatica sulla vetta del Monte Cimone gestita dal CNR. Partenza ore 7, viaggio in corriera fino a quota 1500 metri s.l.m circa, poi a piedi fino alla vetta, a 2165 metri. Temperatura variabile da +3 gradi a -0.1, sulla vetta è venuta anche giù un po' di neve.
Alla stazione una ricercatrice ci ha mostrato tutta la strumentazione disponibile, ci ha spiegato il tipo di misurazioni che fanno, ci ha detto che il livello di anidride carbonica non è mai stato così alto, che invece la temperatura media della terra è stata anche più alta, in passato, ma che ciò che preoccupa gli scienziati oggi è la sua rapidità di variazione. Ci ha raccontato che si sta osservando un lento ma costante calo dei CFC, e un lento ma costante aumento dei loro sostituti: la coperta è sempre corta, i sostituiti dei CFC non danneggiano l'ozono ma aumentano l'effetto serra. Ci ha parlato del lavoro che fanno i ricercatori lassù, ha risposto alle domande degli studenti, è stata molto gentile e disponibile.
In sostanza, nessuna velina supergnocca può competere in fascino con una donna intelligente.
Alla stazione una ricercatrice ci ha mostrato tutta la strumentazione disponibile, ci ha spiegato il tipo di misurazioni che fanno, ci ha detto che il livello di anidride carbonica non è mai stato così alto, che invece la temperatura media della terra è stata anche più alta, in passato, ma che ciò che preoccupa gli scienziati oggi è la sua rapidità di variazione. Ci ha raccontato che si sta osservando un lento ma costante calo dei CFC, e un lento ma costante aumento dei loro sostituti: la coperta è sempre corta, i sostituiti dei CFC non danneggiano l'ozono ma aumentano l'effetto serra. Ci ha parlato del lavoro che fanno i ricercatori lassù, ha risposto alle domande degli studenti, è stata molto gentile e disponibile.
In sostanza, nessuna velina supergnocca può competere in fascino con una donna intelligente.
Verso l'infinito, ma con calma - immersioni di lampadine
Abbiamo visto che esiste una corrispondenza biunivoca tra le successioni binarie infinite non definitivamente uguali e 1 e i numeri appartenenti all'intervallo [0,1).
Siccome queste successioni binarie costituiscono un sottoinsieme dell'insieme di tutte le successioni binarie (che ha cardinalità 2ℵ0), abbiamo concluso che c è minore o uguale di 2ℵ0.
Ora facciamo il contrario, cioè immergiamo l'insieme di tutte le successioni binarie nell'insieme delle successioni binarie non definitivamente uguali a zero.
“Ma come, prima dici che un insieme è contenuto in un altro, e poi dici che il secondo è contenuto nel primo?”.
“Non ho proprio detto così. Ho detto che immergiamo un insieme grande dentro a un insieme piccolo. Cioè facciamo vedere che esiste una funzione iniettiva che va da uno all'altro. Così come esiste una funzione iniettiva che va dall'insieme dei numeri naturali a quello dei numeri pari”.
“Uffa, un altro dei soliti paradossi?”.
“Un altro, o forse sempre lo stesso visto da punti di vista differenti”.
“Va bene, ormai mi ci hai abituato. Vediamo come si fa”.
“È molto semplice, questa volta. Si fa come ha fatto l'albergatore dell'albergo di Hilbert”.
“Sposti la gente?”.
“In un certo senso, sì. Supponi di avere una successione binaria qualunque, come questa: a0, a1, a2, ...”.
“Ok. Immagino che tutti i vari ai possano essere 0 oppure 1, senza alcuna limitazione?”.
“Proprio così. Per costruire la corrispondenza, facciamo così. Ad ogni successione binaria come quella di prima associamo questa successione: a0, 0, a1, 0, a2, 0, ...”.
“Geniale! Assomiglia proprio all'albergo di Hilbert. Queste successioni non sono definitivamente uguali a 1, perché hai alternato tutti gli elementi con uno zero!”.
“Quindi abbiamo definito una corrispondenza iniettiva tra tutte le successioni binarie e un loro sottoinsieme proprio”.
“È vero. Parlando di cardinalità, cosa abbiamo ottenuto?”.
“Che 2ℵ0 è minore o uguale di c”.
“Ma avevamo appena ottenuto un risultato contrario!”.
“Bè, non proprio contrario. Avevamo detto che c è minore o uguale a 2ℵ0”.
“Ah, già, c'è l'uguale che ci salva. Quindi possiamo concludere subito che c e 2ℵ0 sono uguali”.
“Ecco, non è così ovvio”.
“A me pare ovvio, scusa. Se prima dici che un numero è minore uguale di un secondo numero, poi dici che il secondo è minore o uguale del primo, allora i due numeri sono uguali, no?”.
“I due numeri, sì. I due cardinali transfiniti sono forse numeri?”.
“Ehm, non sono proprio numeri naturali, no”.
“E dunque bisogna dimostrare la tua affermazione”.
“Uffa”.
“Che si chiama proprietà di tricotomia”.
“L'arte di tagliare il capello? Mi sembra un nome molto azzeccato, deve essere stato uno dei tuoi Veri Matematici Spiritosi a trovarlo. Certo, io avrei usato tetratricotomia”.
“Ehm, no, sarebbe semplicemente il verificarsi di una sola proprietà tra tre esistenti”.
Siccome queste successioni binarie costituiscono un sottoinsieme dell'insieme di tutte le successioni binarie (che ha cardinalità 2ℵ0), abbiamo concluso che c è minore o uguale di 2ℵ0.
Ora facciamo il contrario, cioè immergiamo l'insieme di tutte le successioni binarie nell'insieme delle successioni binarie non definitivamente uguali a zero.
“Ma come, prima dici che un insieme è contenuto in un altro, e poi dici che il secondo è contenuto nel primo?”.
“Non ho proprio detto così. Ho detto che immergiamo un insieme grande dentro a un insieme piccolo. Cioè facciamo vedere che esiste una funzione iniettiva che va da uno all'altro. Così come esiste una funzione iniettiva che va dall'insieme dei numeri naturali a quello dei numeri pari”.
“Uffa, un altro dei soliti paradossi?”.
“Un altro, o forse sempre lo stesso visto da punti di vista differenti”.
“Va bene, ormai mi ci hai abituato. Vediamo come si fa”.
“È molto semplice, questa volta. Si fa come ha fatto l'albergatore dell'albergo di Hilbert”.
“Sposti la gente?”.
“In un certo senso, sì. Supponi di avere una successione binaria qualunque, come questa: a0, a1, a2, ...”.
“Ok. Immagino che tutti i vari ai possano essere 0 oppure 1, senza alcuna limitazione?”.
“Proprio così. Per costruire la corrispondenza, facciamo così. Ad ogni successione binaria come quella di prima associamo questa successione: a0, 0, a1, 0, a2, 0, ...”.
“Geniale! Assomiglia proprio all'albergo di Hilbert. Queste successioni non sono definitivamente uguali a 1, perché hai alternato tutti gli elementi con uno zero!”.
“Quindi abbiamo definito una corrispondenza iniettiva tra tutte le successioni binarie e un loro sottoinsieme proprio”.
“È vero. Parlando di cardinalità, cosa abbiamo ottenuto?”.
“Che 2ℵ0 è minore o uguale di c”.
“Ma avevamo appena ottenuto un risultato contrario!”.
“Bè, non proprio contrario. Avevamo detto che c è minore o uguale a 2ℵ0”.
“Ah, già, c'è l'uguale che ci salva. Quindi possiamo concludere subito che c e 2ℵ0 sono uguali”.
“Ecco, non è così ovvio”.
“A me pare ovvio, scusa. Se prima dici che un numero è minore uguale di un secondo numero, poi dici che il secondo è minore o uguale del primo, allora i due numeri sono uguali, no?”.
“I due numeri, sì. I due cardinali transfiniti sono forse numeri?”.
“Ehm, non sono proprio numeri naturali, no”.
“E dunque bisogna dimostrare la tua affermazione”.
“Uffa”.
“Che si chiama proprietà di tricotomia”.
“L'arte di tagliare il capello? Mi sembra un nome molto azzeccato, deve essere stato uno dei tuoi Veri Matematici Spiritosi a trovarlo. Certo, io avrei usato tetratricotomia”.
“Ehm, no, sarebbe semplicemente il verificarsi di una sola proprietà tra tre esistenti”.
lunedì 22 settembre 2008
Il senso del tempo
“Buongiorno!”.
“Buongiorno, prof”.
“Bene, ci siete tutti?
“Sì”.
“Vediamo, il registro... dunque, oggi è il 22. Ah, oggi c'è l'equinozio”.
“Di cosa, prof?”.
“Buongiorno, prof”.
“Bene, ci siete tutti?
“Sì”.
“Vediamo, il registro... dunque, oggi è il 22. Ah, oggi c'è l'equinozio”.
“Di cosa, prof?”.
Verso l'infinito, ma con calma - lampadine e numeri reali
Abbiamo detto che dei numeri reali ci interessa una sola cosa: possono essere espressi come numeri decimali finiti oppure infiniti. Ora prendiamo solo una parte dei numeri reali, l'intervallo [0,1). In pratica, stiamo considerando tutti i numeri che si possono scrivere come zero virgola qualcosa.
“Come mai prendi solo un intervallo, invece di prendere tutti i numeri reali?”.
“Per comodità, tanto poi si dimostra che un intervallo e l'intera retta hanno la stessa cardinalità”.
“Ma come è possibile? Un altro paradosso dell'infinito?”.
“Già. Però lo vediamo più avanti. Adesso ci concentriamo sull'intervallo [0,1) e le successioni binarie infinite”.
“Ah, torniamo a parlare di lampadine?”.
“Sì, però questa volta consideriamo soltanto le successioni binarie che non sono definitivamente uguali a 1”.
“Eh?”.
“Definitivamente significa da un certo punto in poi. Insomma, non vogliamo le successioni binarie che terminano con infinite cifre uguali a 1”.
“Ah, ok. Non capisco però il perché di questa limitazione”.
“Te lo spiego tra un attimo. Prima ti dico che le successioni binarie infinite possono essere interpretate come la parte dopo la virgola di un numero compreso tra 0 e 1, purché lo trasformiamo in binario”.
“Ah! La numerazione binaria. Ma si possono trasformare in binario anche numeri decimali?”.
“Certo, così come 0.110 significa 10-1, 0.12 significa 2-1”.
“Bene, ogni giorno si impara una cosa nuova”.
“Ora si spiega anche il motivo per cui non prendiamo le successioni definitivamente uguali a 1. Così come in base 10 non esiste il periodo 9, in base 2 non esiste il periodo 1”.
“Va bene. Cosa vogliamo dimostrare, allora?”.
“Praticamente l'abbiamo già fatto: esiste una corrispondenza biunivoca tra le successioni binarie infinite non definitivamente uguali a 1 e i numeri appartenenti all'intervallo [0,1)”.
“Ah, già, è vero”.
“E quindi, se indichiamo con c (che sarebbe poi il famoso c gotico) la cardinalità di [0,1), abbiamo che c è minore o uguale di 2ℵ0”.
“Com'è che dici minore o uguale?”.
“Perché le successioni binarie non definitivamente uguali a 1 sono un sottoinsieme di tutte le successioni binarie, che hanno cardinalità 2ℵ0”.
“E allora, visto che sono di meno, non dovresti dire minore invece di minore o uguale?”.
“Dimentichi l'albergo di Hilbert”.
“Uhm, cosa c'entra?”.
“Era un paradosso che ti faceva capire che un insieme infinito e un suo sottoinsieme proprio possono avere la stessa cardinalità”.
“Ah, è vero! Avevi spostato gli infiniti ospiti nelle camere pari”.
“Dimostrando che l'insieme dei numeri pari e quello dei numeri naturali hanno la stessa cardinalità”.
“Ecco spiegato il minore o uguale: è possibile che le successioni binarie e il sottoinsieme di quelle non definitivamente uguali a 1 abbiano la stessa cardinalità”.
“Proprio così”.
“E come facciamo a sapere se è vero il minore oppure l'uguale?”.
“Non è semplice: servono un'altra funzione e un teorema dal nome altisonante”.
“Come mai prendi solo un intervallo, invece di prendere tutti i numeri reali?”.
“Per comodità, tanto poi si dimostra che un intervallo e l'intera retta hanno la stessa cardinalità”.
“Ma come è possibile? Un altro paradosso dell'infinito?”.
“Già. Però lo vediamo più avanti. Adesso ci concentriamo sull'intervallo [0,1) e le successioni binarie infinite”.
“Ah, torniamo a parlare di lampadine?”.
“Sì, però questa volta consideriamo soltanto le successioni binarie che non sono definitivamente uguali a 1”.
“Eh?”.
“Definitivamente significa da un certo punto in poi. Insomma, non vogliamo le successioni binarie che terminano con infinite cifre uguali a 1”.
“Ah, ok. Non capisco però il perché di questa limitazione”.
“Te lo spiego tra un attimo. Prima ti dico che le successioni binarie infinite possono essere interpretate come la parte dopo la virgola di un numero compreso tra 0 e 1, purché lo trasformiamo in binario”.
“Ah! La numerazione binaria. Ma si possono trasformare in binario anche numeri decimali?”.
“Certo, così come 0.110 significa 10-1, 0.12 significa 2-1”.
“Bene, ogni giorno si impara una cosa nuova”.
“Ora si spiega anche il motivo per cui non prendiamo le successioni definitivamente uguali a 1. Così come in base 10 non esiste il periodo 9, in base 2 non esiste il periodo 1”.
“Va bene. Cosa vogliamo dimostrare, allora?”.
“Praticamente l'abbiamo già fatto: esiste una corrispondenza biunivoca tra le successioni binarie infinite non definitivamente uguali a 1 e i numeri appartenenti all'intervallo [0,1)”.
“Ah, già, è vero”.
“E quindi, se indichiamo con c (che sarebbe poi il famoso c gotico) la cardinalità di [0,1), abbiamo che c è minore o uguale di 2ℵ0”.
“Com'è che dici minore o uguale?”.
“Perché le successioni binarie non definitivamente uguali a 1 sono un sottoinsieme di tutte le successioni binarie, che hanno cardinalità 2ℵ0”.
“E allora, visto che sono di meno, non dovresti dire minore invece di minore o uguale?”.
“Dimentichi l'albergo di Hilbert”.
“Uhm, cosa c'entra?”.
“Era un paradosso che ti faceva capire che un insieme infinito e un suo sottoinsieme proprio possono avere la stessa cardinalità”.
“Ah, è vero! Avevi spostato gli infiniti ospiti nelle camere pari”.
“Dimostrando che l'insieme dei numeri pari e quello dei numeri naturali hanno la stessa cardinalità”.
“Ecco spiegato il minore o uguale: è possibile che le successioni binarie e il sottoinsieme di quelle non definitivamente uguali a 1 abbiano la stessa cardinalità”.
“Proprio così”.
“E come facciamo a sapere se è vero il minore oppure l'uguale?”.
“Non è semplice: servono un'altra funzione e un teorema dal nome altisonante”.
sabato 20 settembre 2008
Mousse
Imbrattando mezza cucina e quindi perdendo un certo quantitativo di punti moglie (nonostante l'attività culinaria di solito ne faccia guadagnare) ho prodotto una meravigliosa mousse al cioccolato, seguendo le istruzioni di Dario Bressanini. Consigliatissima (deve piacere il cioccolato fondente, eh).
Verso l'infinito, ma con calma - i numeri reali
Siamo arrivati al punto in cui ci tocca parlare dei numeri reali, cosa che ogni Vero Matematico preferirebbe non fare, perché la loro definizione è complicata e tutti comunque li conoscono.
Per prima cosa, i numeri reali possono essere costruiti o definiti. Il vantaggio del primo approccio è la sua intrinseca eleganza: i reali si costruiscono a partire dai razionali, i razionali dagli interi, gli interi dai naturali, i naturali dall'insieme vuoto. Basta quindi il solo concetto di insieme vuoto per ottenere tutto. Lo svantaggio è che la costruzione è strana e complicata. Anzi, di costruzioni ce ne sono più di una.
Si possono usare le successioni di Cauchy, che sono successioni i cui termini si avvicinano sempre di più fra loro. Parlando molto a braccio e intuitivamente, i numeri reali sono l'insieme in cui tutte le successioni di Cauchy convergono. Nell'insieme dei numeri razionali potrebbero esserci invece problemi di convergenza. Prendiamo per esempio la seguente successione:
Essa è composta solo da frazioni, è di Cauchy, ma non converge a una frazione (perché converge a radice di due, che non è razionale).
Oppure si potrebbero usare le sezioni di Dedekind, che sono un concetto ancora più complicato da descrivere. Parlando in maniera sempre meno rigorosa, le sezioni di Dedekind ci fanno capire che l'insieme dei numeri razionali, pur essendo denso, ha dei buchi. Denso significa che comunque scelgo due numeri, tra di essi ne trovo almeno un altro. I buchi corrispondono ai numeri irrazionali. Per esempio, se consideriamo i due seguenti insiemi:
ci accorgiamo che gli elementi contenuti in essi si avvicinano sempre di più tra loro e si addensano attorno a un buco: il posto occupato dalla radice di due.
Se noi allora chiamiamo numeri reali tutti gli oggetti individuati dalle sezioni di Dedekind, in un certo senso riempiamo i buchi sulla retta dei numeri e completiamo l'insieme dei numeri razionali, ottenendo i reali.
I numeri reali possono anche essere definiti come numeri decimali (illimitati oppure no). Dopodiché si definiscono le operazioni in modo formale, e da lì ci si ricollega agli altri numeri, mostrando che questa definizione comprende anche i numeri naturali, interi e razionali.
Oppure si può partire dai numeri iperrazionali (che sarebbero i razionali dell'analisi non standard). Oppure ancora dai numeri surreali (e questa è la parte che mi affascina di più, che mi piacerebbe approfondire e sulla quale vorrei scrivere qualcosa).
Insomma, le costruzioni dei numeri reali sono tante, tutte complicate. Complicate anche dal fatto che non solo occorre definire i numeri, ma poi è necessario fare vedere come funzionano le operazioni tra di essi, e mostrare che queste nuove definizioni sono in accordo con le vecchie. Perciò è necessario fare vedere che uno più uno fa ancora due. Ecco perché i matematici preferirebbero non costruire i numeri reali.
Esiste un'altra strada, alternativa a quella delle costruzioni: è la strada della assiomatizzazione. Cioè, noi non costruiamo niente, ma diciamo semplicemente che i numeri reali sono l'unico campo ordinato archimedeo completo.
“Ah, certo, semplicemente”.
“Eh, hai ragione, non è semplice nemmeno questo”.
“Anche se, in fondo, ci sono solo quattro parole che mi devi spiegare”.
“Sì, e tieni presente che queste quattro parole implicano una serie di proprietà sovrabbondanti, nel senso che alcune dipendono da altre. Le si potrebbe restringere ulteriormente, come ha fatto Tarski, ma si perde un po' in chiarezza. Non posso però fare a meno di citarti l'ultimo assioma di Tarski”.
“Perché? È incomprensibile? Complicato? Astruso?”.
“Giudica tu. Dice che 1 è minore di 1+1”.
“Forse è meglio se torniamo a quelle quattro parole da spiegare: cominciamo da campo?”.
“Ok. Campo è una struttura algebrica composta da un insieme e due operazioni”.
“Va bene. Suppongo che l'insieme sia quello dei numeri, e le due operazioni siano operazioni su quei numeri?”.
“Certamente. La prima operazione la indichiamo con + e la seconda con ·”.
“Va bene. Tutto qua?”.
“No, le operazioni devono soddisfare a certe proprietà. L'operazione +, che chiamiamo somma, deve essere associativa e commutativa. Poi deve esistere l'elemento neutro, che indichiamo con 0, e deve esistere l'inverso”.
“Va bene, questi sono concetti che si imparano anche alle elementari. Ci sono proprietà anche per il · (posso chiamarlo prodotto)?”.
“Sì, il prodotto deve essere associativo, commutativo, deve esistere l'elemento neutro che indichiamo con 1, e ogni elemento diverso dallo 0 deve possedere il reciproco”.
“Stai ripetendo le proprietà della somma e del prodotto delle normali operazioni, in effetti”.
“Certo. Attento però che sto assiomatizzando, cioè non sto dicendo che un certo insieme e una certa operazione godono di certe proprietà, ma sto facendo il contrario: sto caratterizzando un insieme dicendoti quali sono le proprietà che deve avere”.
“In pratica tu mi dai le proprietà, e io devo immaginarmi l'insieme”.
“Sì, esatto. I filosofi si divertono molto su questo punto, perché ora non stiamo parlando di una cosa in sé, di cui studiamo le proprietà, ma di un oggetto che esiste solo in quanto possiede certe proprietà. Ti dirò anche che personalmente questo secondo aspetto mi piace di meno”.
“Cioè per te gli oggetti matematici esistono, in un qualche modo?”.
“Eh, sì”.
“Sei proprio un Vero Matematico”.
“Grazie”.
“...”.
“O forse non intendevi farmi un complimento?”.
“Ehm, dicevamo delle proprietà dei numeri reali?”.
“Eh, andiamo avanti che è meglio, va... Dunque, deve essere anche vera la proprietà distributiva del prodotto rispetto alla somma. E con queste proprietà abbiamo definito il concetto di campo”.
“Ok, passiamo alla prossima parola: ordinato”.
“Ordinato è facile: esiste un ordine tra tutti gli elementi. Cioè, comunque tu scegli due elementi, puoi dire se sono uguali o se uno è minore (o maggiore) dell'altro”.
“Va bene. Archimedeo?”.
“Archimedeo significa che non ci sono numeri piccoli e numeri grandi in assoluto. Non puoi fare una cosa come scegliere un numero talmente grande e uno talmente piccolo che, moltiplicando il piccolo tante volte quante vuoi, non riesci mai a superare il grande. Lo spiega bene .mau. quando dice che 0.(9) è uguale a 1. E mostra anche un esempio di insieme numerico in cui manca la proprietà archimedea, quando dice che 0.(9) non è uguale a 1”.
“Ah, questo è più complicato rispetto alle altre proprietà. Comunque ho capito, non esistono quelle cose strane come gli infinitesimi”.
“Perfetto. Completo invece significa che ogni sottoinsieme non vuoto e superiormente limitato ammette estremo superiore”.
“Questo è meno chiaro”.
“Significa questo: prendi un sottoinsieme dei numeri, che non sia l'insieme vuoto”.
“Ok”.
“Questo insieme deve essere superiormente limitato, cioè tutti i suoi elementi devono essere più piccoli di un qualche elemento prefissato”.
“Bene”.
“Ti faccio notare che se, per esempio, tutti gli elementi sono minori di 10, essi sono minori anche di 15, di 20, oppure di 42”.
“Certo, è chiaro. Se non vado oltre un certo ostacolo, non vado nemmeno oltre un ostacolo più grande”.
“Bene. Questi ostacoli si chiamano maggioranti. Prendi il più piccolo di tutti gli ostacoli: questo si chiama estremo superiore”.
“E secondo la tua definizione, l'estremo superiore deve appartenere all'insieme?”.
“Sì”.
“E non appartiene sempre all'insieme?”.
“Solo se l'insieme è quello dei numeri reali. Prendi questa nostra vecchia conoscenza:”.
“Ah, sempre lui! Ho capito: gli elementi non superano mai radice di due, ma radice di due non appartiene all'insieme perché non è una frazione. E quindi lascia un buco”.
“Certo. Il concetto di completezza è proprio legato a questa faccenda dei buchi”.
“Insomma, alla fine l'assiomatizzazione non è così complicata”.
“Ecco, vedi, tu avevi detto che c'erano quattro parole da spiegare”.
“Campo. Ordinato. Archimedeo. Completo. Non sono quattro?”.
“Hai dimenticato unico”.
“Ohi ohi.”.
“Si tratterebbe di dimostrare che questa serie di assiomi ha un unico modello”.
“Ed è difficile?”.
“Sì”.
“Lungo?”.
“Sì”.
“Lo facciamo?”.
“No. A noi dei reali interessa solo questa piccola cosa: sono numeri decimali finiti oppure infiniti”.
“E non potevi dirlo subito?”.
“Per risparmiarti quel senso di frustrazione che hanno i Veri Matematici tutte le volte che devono definire i numeri reali? No, la strada per diventare un Vero Matematico è lunga e piena di ostacoli”.
Per prima cosa, i numeri reali possono essere costruiti o definiti. Il vantaggio del primo approccio è la sua intrinseca eleganza: i reali si costruiscono a partire dai razionali, i razionali dagli interi, gli interi dai naturali, i naturali dall'insieme vuoto. Basta quindi il solo concetto di insieme vuoto per ottenere tutto. Lo svantaggio è che la costruzione è strana e complicata. Anzi, di costruzioni ce ne sono più di una.
Si possono usare le successioni di Cauchy, che sono successioni i cui termini si avvicinano sempre di più fra loro. Parlando molto a braccio e intuitivamente, i numeri reali sono l'insieme in cui tutte le successioni di Cauchy convergono. Nell'insieme dei numeri razionali potrebbero esserci invece problemi di convergenza. Prendiamo per esempio la seguente successione:
1, 1.4, 1.41, 1.414, 1.4142, 1.41421, 1.414213, ...
Essa è composta solo da frazioni, è di Cauchy, ma non converge a una frazione (perché converge a radice di due, che non è razionale).
Oppure si potrebbero usare le sezioni di Dedekind, che sono un concetto ancora più complicato da descrivere. Parlando in maniera sempre meno rigorosa, le sezioni di Dedekind ci fanno capire che l'insieme dei numeri razionali, pur essendo denso, ha dei buchi. Denso significa che comunque scelgo due numeri, tra di essi ne trovo almeno un altro. I buchi corrispondono ai numeri irrazionali. Per esempio, se consideriamo i due seguenti insiemi:
A = {1, 1.4, 1.41, 1.414, 1.4142, 1.41421, 1.414213, ...}
B = {2, 1.5, 1.42, 1.415, 1.4143, 1.41422, 1.414214, ...}
ci accorgiamo che gli elementi contenuti in essi si avvicinano sempre di più tra loro e si addensano attorno a un buco: il posto occupato dalla radice di due.
Se noi allora chiamiamo numeri reali tutti gli oggetti individuati dalle sezioni di Dedekind, in un certo senso riempiamo i buchi sulla retta dei numeri e completiamo l'insieme dei numeri razionali, ottenendo i reali.
I numeri reali possono anche essere definiti come numeri decimali (illimitati oppure no). Dopodiché si definiscono le operazioni in modo formale, e da lì ci si ricollega agli altri numeri, mostrando che questa definizione comprende anche i numeri naturali, interi e razionali.
Oppure si può partire dai numeri iperrazionali (che sarebbero i razionali dell'analisi non standard). Oppure ancora dai numeri surreali (e questa è la parte che mi affascina di più, che mi piacerebbe approfondire e sulla quale vorrei scrivere qualcosa).
Insomma, le costruzioni dei numeri reali sono tante, tutte complicate. Complicate anche dal fatto che non solo occorre definire i numeri, ma poi è necessario fare vedere come funzionano le operazioni tra di essi, e mostrare che queste nuove definizioni sono in accordo con le vecchie. Perciò è necessario fare vedere che uno più uno fa ancora due. Ecco perché i matematici preferirebbero non costruire i numeri reali.
Esiste un'altra strada, alternativa a quella delle costruzioni: è la strada della assiomatizzazione. Cioè, noi non costruiamo niente, ma diciamo semplicemente che i numeri reali sono l'unico campo ordinato archimedeo completo.
“Ah, certo, semplicemente”.
“Eh, hai ragione, non è semplice nemmeno questo”.
“Anche se, in fondo, ci sono solo quattro parole che mi devi spiegare”.
“Sì, e tieni presente che queste quattro parole implicano una serie di proprietà sovrabbondanti, nel senso che alcune dipendono da altre. Le si potrebbe restringere ulteriormente, come ha fatto Tarski, ma si perde un po' in chiarezza. Non posso però fare a meno di citarti l'ultimo assioma di Tarski”.
“Perché? È incomprensibile? Complicato? Astruso?”.
“Giudica tu. Dice che 1 è minore di 1+1”.
“Forse è meglio se torniamo a quelle quattro parole da spiegare: cominciamo da campo?”.
“Ok. Campo è una struttura algebrica composta da un insieme e due operazioni”.
“Va bene. Suppongo che l'insieme sia quello dei numeri, e le due operazioni siano operazioni su quei numeri?”.
“Certamente. La prima operazione la indichiamo con + e la seconda con ·”.
“Va bene. Tutto qua?”.
“No, le operazioni devono soddisfare a certe proprietà. L'operazione +, che chiamiamo somma, deve essere associativa e commutativa. Poi deve esistere l'elemento neutro, che indichiamo con 0, e deve esistere l'inverso”.
“Va bene, questi sono concetti che si imparano anche alle elementari. Ci sono proprietà anche per il · (posso chiamarlo prodotto)?”.
“Sì, il prodotto deve essere associativo, commutativo, deve esistere l'elemento neutro che indichiamo con 1, e ogni elemento diverso dallo 0 deve possedere il reciproco”.
“Stai ripetendo le proprietà della somma e del prodotto delle normali operazioni, in effetti”.
“Certo. Attento però che sto assiomatizzando, cioè non sto dicendo che un certo insieme e una certa operazione godono di certe proprietà, ma sto facendo il contrario: sto caratterizzando un insieme dicendoti quali sono le proprietà che deve avere”.
“In pratica tu mi dai le proprietà, e io devo immaginarmi l'insieme”.
“Sì, esatto. I filosofi si divertono molto su questo punto, perché ora non stiamo parlando di una cosa in sé, di cui studiamo le proprietà, ma di un oggetto che esiste solo in quanto possiede certe proprietà. Ti dirò anche che personalmente questo secondo aspetto mi piace di meno”.
“Cioè per te gli oggetti matematici esistono, in un qualche modo?”.
“Eh, sì”.
“Sei proprio un Vero Matematico”.
“Grazie”.
“...”.
“O forse non intendevi farmi un complimento?”.
“Ehm, dicevamo delle proprietà dei numeri reali?”.
“Eh, andiamo avanti che è meglio, va... Dunque, deve essere anche vera la proprietà distributiva del prodotto rispetto alla somma. E con queste proprietà abbiamo definito il concetto di campo”.
“Ok, passiamo alla prossima parola: ordinato”.
“Ordinato è facile: esiste un ordine tra tutti gli elementi. Cioè, comunque tu scegli due elementi, puoi dire se sono uguali o se uno è minore (o maggiore) dell'altro”.
“Va bene. Archimedeo?”.
“Archimedeo significa che non ci sono numeri piccoli e numeri grandi in assoluto. Non puoi fare una cosa come scegliere un numero talmente grande e uno talmente piccolo che, moltiplicando il piccolo tante volte quante vuoi, non riesci mai a superare il grande. Lo spiega bene .mau. quando dice che 0.(9) è uguale a 1. E mostra anche un esempio di insieme numerico in cui manca la proprietà archimedea, quando dice che 0.(9) non è uguale a 1”.
“Ah, questo è più complicato rispetto alle altre proprietà. Comunque ho capito, non esistono quelle cose strane come gli infinitesimi”.
“Perfetto. Completo invece significa che ogni sottoinsieme non vuoto e superiormente limitato ammette estremo superiore”.
“Questo è meno chiaro”.
“Significa questo: prendi un sottoinsieme dei numeri, che non sia l'insieme vuoto”.
“Ok”.
“Questo insieme deve essere superiormente limitato, cioè tutti i suoi elementi devono essere più piccoli di un qualche elemento prefissato”.
“Bene”.
“Ti faccio notare che se, per esempio, tutti gli elementi sono minori di 10, essi sono minori anche di 15, di 20, oppure di 42”.
“Certo, è chiaro. Se non vado oltre un certo ostacolo, non vado nemmeno oltre un ostacolo più grande”.
“Bene. Questi ostacoli si chiamano maggioranti. Prendi il più piccolo di tutti gli ostacoli: questo si chiama estremo superiore”.
“E secondo la tua definizione, l'estremo superiore deve appartenere all'insieme?”.
“Sì”.
“E non appartiene sempre all'insieme?”.
“Solo se l'insieme è quello dei numeri reali. Prendi questa nostra vecchia conoscenza:”.
{1, 1.4, 1.41, 1.414, 1.4142, 1.41421, 1.414213, ...}
“Ah, sempre lui! Ho capito: gli elementi non superano mai radice di due, ma radice di due non appartiene all'insieme perché non è una frazione. E quindi lascia un buco”.
“Certo. Il concetto di completezza è proprio legato a questa faccenda dei buchi”.
“Insomma, alla fine l'assiomatizzazione non è così complicata”.
“Ecco, vedi, tu avevi detto che c'erano quattro parole da spiegare”.
“Campo. Ordinato. Archimedeo. Completo. Non sono quattro?”.
“Hai dimenticato unico”.
“Ohi ohi.”.
“Si tratterebbe di dimostrare che questa serie di assiomi ha un unico modello”.
“Ed è difficile?”.
“Sì”.
“Lungo?”.
“Sì”.
“Lo facciamo?”.
“No. A noi dei reali interessa solo questa piccola cosa: sono numeri decimali finiti oppure infiniti”.
“E non potevi dirlo subito?”.
“Per risparmiarti quel senso di frustrazione che hanno i Veri Matematici tutte le volte che devono definire i numeri reali? No, la strada per diventare un Vero Matematico è lunga e piena di ostacoli”.
venerdì 19 settembre 2008
Verso l'infinito, ma con calma - infinite lampadine
Una successione è una funzione che ha, come insieme di partenza, l'insieme dei numeri naturali. In altre parole, è uno strumento che conta. Ogni volta che contiamo un insieme di oggetti associamo un numero naturale a ogni oggetto, in ordine: in pratica stiamo costruendo una successione; con la differenza che noi, a un certo punto, ci fermiamo, mentre le successioni matematiche vanno avanti sempre.
Bene, ora consideriamo una successione per la quale l'insieme di arrivo sia {0,1}. Come è fatta?
Ad ogni numero naturale sarà associato uno 0 oppure un 1, non ci sono altre possibilità. Ecco un esempio:
In questa successione 0 è associato a 0, 1 a 1, poi 2 è associato nuovamente a 0, 3 a 1, e così via. Siccome l'insieme di partenza di ogni successione è prefissato, possiamo anche ometterlo (tanto sappiamo contare, basta che teniamo in mente che partiamo da zero). In questo caso, la successione di prima diventa più semplice da scrivere:
Si tratta di una stringa infinita composta solo da cifre 0 e 1: la chiamiamo successione binaria (infinita).
Se utilizziamo l'esempio delle lampadine accese e spente, una successione binaria infinita diventa una fila infinita di lampadine, ognuna delle quali può essere accesa o spenta.
Ora, di queste successioni binarie ce ne sono tante.
“Quante?”.
“Tante quanti sono gli elementi di P(N)”.
“L'insieme dei sottoinsiemi dei numeri naturali?”.
“Giusto”.
“Quindi dovrebbe essere 2ℵ0, dato che abbiamo visto che la cardinalità dell'insieme dei naturali è ℵ0, e che se la cardinalità di un insieme è α, allora la cardinalità dell'insieme delle parti è 2α. Giusto?”.
“Proprio così”.
“Ed è difficile da dimostrare?”.
“No, è abbastanza semplice. Usiamo la tecnica che abbiamo già usato per dimostrare che la cardinalità dell'insieme delle parti di un insieme dato è maggiore di quella dell'insieme”.
“Anche allora avevamo parlato di lampadine, se ben ricordo”.
“Infatti è così. Le nostre successioni binarie associano i numeri naturali a 0 oppure a 1, cioè a una lampadina spenta oppure accesa. Bene, allora a una data successione associamo il sottoinsieme dei numeri naturali che contiene tutti i numeri per i quali sono accese le lampadine”.
“Uhm. Un esempio?”.
“Prendi la successione 01010101...”.
“Ok. A 0 è associato il primo numero, che è 0, quindi lampadina spenta. Non ci interessa. A 1 è associato 1, lampadina accesa, bene. A 2 è associato 0. Ho capito, questa successione accende lampadine solo per i numeri dispari”.
“E quindi ad essa sarà associato l'insieme di tutti i numeri dispari, sottoinsieme di N”.
“Ok, chiaro, ho capito”.
“Prova a scrivere la successione che sarà associata ai numeri pari”.
“Facile: 10101010...”.
“Quindi a ogni successione è associato un sottoinsieme, e se due successioni sono diverse, sarà diverso anche l'insieme corrispondente”.
“Ok”.
“Ora vediamo il contrario: a ogni sottoinsieme A di N è associata una successione binaria”.
“Ah, sì, è facile anche questo: basta cominciare a contare da 0 e accendere una lampadina quando si incontra un numero che sta in A”.
“Molto bene. Per esempio, quale successione è associata a {1,2,3}?”.
“Dovrebbe essere 111”.
“No, non va bene, ricordati che i Veri Matematici non cominciano a contare da 1”.
“Ah, già, si parte da 0. Allora è questa: 0111”.
“Quasi. Questa, in effetti, non è una successione infinita”.
“Ah. Ma dopo non ci sono più numeri, mi hai dato un insieme finito... Bé, posso continuare con una successione di 0”.
“E quindi, quale successione è associata a {1,2,3}?”.
“Questa: 011100000...”.
“Ottimo. Riassumendo: esiste una corrispondenza biunivoca tra le successioni binarie (infinite) e l'insieme delle parti dei numeri naturali”.
“E quindi i due insiemi hanno la stessa cardinalità, che è maggiore di quella dei numeri naturali e che abbiamo indicato con 2ℵ0. Ma perché abbiamo dimostrato questo teorema?”.
“Perché ci sarà utile nello studio della cardinalità dei numeri reali”.
Bene, ora consideriamo una successione per la quale l'insieme di arrivo sia {0,1}. Come è fatta?
Ad ogni numero naturale sarà associato uno 0 oppure un 1, non ci sono altre possibilità. Ecco un esempio:
0-0 1-1 2-0 3-1 4-0 5-1 ...
In questa successione 0 è associato a 0, 1 a 1, poi 2 è associato nuovamente a 0, 3 a 1, e così via. Siccome l'insieme di partenza di ogni successione è prefissato, possiamo anche ometterlo (tanto sappiamo contare, basta che teniamo in mente che partiamo da zero). In questo caso, la successione di prima diventa più semplice da scrivere:
01010101...
Si tratta di una stringa infinita composta solo da cifre 0 e 1: la chiamiamo successione binaria (infinita).
Se utilizziamo l'esempio delle lampadine accese e spente, una successione binaria infinita diventa una fila infinita di lampadine, ognuna delle quali può essere accesa o spenta.
Ora, di queste successioni binarie ce ne sono tante.
“Quante?”.
“Tante quanti sono gli elementi di P(N)”.
“L'insieme dei sottoinsiemi dei numeri naturali?”.
“Giusto”.
“Quindi dovrebbe essere 2ℵ0, dato che abbiamo visto che la cardinalità dell'insieme dei naturali è ℵ0, e che se la cardinalità di un insieme è α, allora la cardinalità dell'insieme delle parti è 2α. Giusto?”.
“Proprio così”.
“Ed è difficile da dimostrare?”.
“No, è abbastanza semplice. Usiamo la tecnica che abbiamo già usato per dimostrare che la cardinalità dell'insieme delle parti di un insieme dato è maggiore di quella dell'insieme”.
“Anche allora avevamo parlato di lampadine, se ben ricordo”.
“Infatti è così. Le nostre successioni binarie associano i numeri naturali a 0 oppure a 1, cioè a una lampadina spenta oppure accesa. Bene, allora a una data successione associamo il sottoinsieme dei numeri naturali che contiene tutti i numeri per i quali sono accese le lampadine”.
“Uhm. Un esempio?”.
“Prendi la successione 01010101...”.
“Ok. A 0 è associato il primo numero, che è 0, quindi lampadina spenta. Non ci interessa. A 1 è associato 1, lampadina accesa, bene. A 2 è associato 0. Ho capito, questa successione accende lampadine solo per i numeri dispari”.
“E quindi ad essa sarà associato l'insieme di tutti i numeri dispari, sottoinsieme di N”.
“Ok, chiaro, ho capito”.
“Prova a scrivere la successione che sarà associata ai numeri pari”.
“Facile: 10101010...”.
“Quindi a ogni successione è associato un sottoinsieme, e se due successioni sono diverse, sarà diverso anche l'insieme corrispondente”.
“Ok”.
“Ora vediamo il contrario: a ogni sottoinsieme A di N è associata una successione binaria”.
“Ah, sì, è facile anche questo: basta cominciare a contare da 0 e accendere una lampadina quando si incontra un numero che sta in A”.
“Molto bene. Per esempio, quale successione è associata a {1,2,3}?”.
“Dovrebbe essere 111”.
“No, non va bene, ricordati che i Veri Matematici non cominciano a contare da 1”.
“Ah, già, si parte da 0. Allora è questa: 0111”.
“Quasi. Questa, in effetti, non è una successione infinita”.
“Ah. Ma dopo non ci sono più numeri, mi hai dato un insieme finito... Bé, posso continuare con una successione di 0”.
“E quindi, quale successione è associata a {1,2,3}?”.
“Questa: 011100000...”.
“Ottimo. Riassumendo: esiste una corrispondenza biunivoca tra le successioni binarie (infinite) e l'insieme delle parti dei numeri naturali”.
“E quindi i due insiemi hanno la stessa cardinalità, che è maggiore di quella dei numeri naturali e che abbiamo indicato con 2ℵ0. Ma perché abbiamo dimostrato questo teorema?”.
“Perché ci sarà utile nello studio della cardinalità dei numeri reali”.
giovedì 18 settembre 2008
Sull'importanza delle dimostrazioni di esistenza
Teorema: nell'insieme dei numeri interi positivi si ha che 1 è il più grande di tutti i numeri.
Dimostrazione: si scelga un qualunque numero diverso da 1 e lo si elevi al quadrato: si otterrà sempre un numero maggiore di quello dato. Dunque nessun numero maggiore di 1 è più grande di tutti gli altri. Per quanto riguarda il numero 1, invece, se lo si eleva al quadrato si ottiene ancora 1. Allora 1 è il maggiore tra tutti gli interi positivi. C.V.D.
Dimostrazione: si scelga un qualunque numero diverso da 1 e lo si elevi al quadrato: si otterrà sempre un numero maggiore di quello dato. Dunque nessun numero maggiore di 1 è più grande di tutti gli altri. Per quanto riguarda il numero 1, invece, se lo si eleva al quadrato si ottiene ancora 1. Allora 1 è il maggiore tra tutti gli interi positivi. C.V.D.
Il problema isoperimetrico
All'università di Modena oggi si sono svolte le premiazioni degli studenti che hanno partecipato alle varie fasi delle olimpiadi della matematica. La cerimonia è stata preceduta da una conferenza dal titolo Cerchi, quadrati e triangoli nella competizione isoperimetrica, grazie alla quale ho imparato:
- che esiste una dimostrazione per via sintetica del problema isoperimetrico (che si trova anche sul Courant-Robbins),
- che esiste un problema isoperimetrico inverso,
- che sono molto importanti le dimostrazioni di esistenza.
Verso l'infinito, ma con calma - esistono cardinalità grandi
So che qui perderò la metà dei miei 102 lettori, perché questa dimostrazione è difficile. Ma se uno prova a seguirla, magari con carta, matita, gomma, troverà che è affascinante. Chiaramente, affascinante per un Vero Matematico.
Abbiamo visto che se la cardinalità dell'insieme A è α allora la cardinalità dell'insieme delle parti P(A) è 2α. Nel caso in cui α è transfinito, la scrittura 2α è soltanto un simbolo. Ora vogliamo dimostrare che 2α è effettivamente maggiore di α anche nel caso transfinito.
Supponiamo per assurdo che esista una funzione biunivoca μ tra A e P(A).
“Ehm, per assurdo?”.
“Sì, è una tecnica di dimostrazione”.
“Uhm”.
“Funziona così: tu supponi che quello che vuoi dimostrare non sia vero, e provi a vedere cosa succede. Se arrivi a una contraddizione, vuol dire che la tua supposizione iniziale è sbagliata, e quindi quello che vuoi dimostrare è proprio vero”.
“Ah. Un metodo un po' strano, ma credo di aver capito. Prova ad andare avanti”.
“Allora, questa fantomatica corrispondenza biunivoca μ dovrebbe far corrispondere elementi di A a sottoinsiemi di A”.
“Giusto: parte da A (che contiene elementi di A, evidentemente) e arriva a P(A) (che contiene sottoinsiemi di A)”.
“Allora, prendiamo un generico elemento di A e chiamiamolo (con grande fantasia) a”.
“I Veri Matematici sono noti per la loro fantasia”.
“È vero. Un mio prof all'università un giorno ci fece una dimostrazione in cui si mise a usare un sacco di lettere strane. Scoprimmo solo alla fine che voleva arrivare a usare la variabile ηβ”.
“Mi avvalgo della facoltà di non commentare”.
“Comunque dicevamo dell'elemento a. Questo corrisponderà a un sottoinsieme di A”.
“Sì, certo”.
“Questo sottoinsieme di A potrebbe contenere l'elemento a oppure no”.
“Uhm. Ok. Magari, un esempietto?”.
“Immagina che l'insieme A sia {Pippo, Pluto, Paperino}, e prendiamo un elemento di questo insieme, per esempio Pippo. A questo elemento corrisponde un sottoinsieme di A, diciamo che sia {Pluto, Paperino}”.
“Ok. In questo caso a non appartiene al corrispondente insieme”.
“Esatto. Se invece prendo Pluto, e immagino che sia associato a {Pippo, Pluto}, allora vedo che a appartiene al corrispondente insieme”.
“Ok, ci sono, ho capito. Tutti gli elementi di A saranno associati a insiemi, e abbiamo due possibilità: o questi insiemi contengono i corrispondenti elementi, oppure non li contengono”.
“Perfetto. Allora possiamo considerare l'insieme di tutti gli elementi di A che non appartengono al corrispondente insieme, come il Pippo dell'esempio precedente”.
“Ok. Immagino che un Vero Matematico lo chiamerebbe B”.
“Vedo che sei sulla buona strada. Ora, attento: anche B è un sottoinsieme di A, vero?”.
“Certo. Contiene solo elementi di A”.
“E quindi questo B, nella nostra fantomatica corrispondenza biunivoca, proviene da un qualche elemento di A”.
“Sì, se immaginiamo che questa corrispondenza biunivoca esista, come hai detto tu, allora B proviene da... possiamo chiamarlo b?”.
“Certo, un'ottima scelta. L'elemento b è associato a B. Ora arriva la domanda: b appartiene a B?”.
“Vediamo: B contiene solo elementi che non appartengono all'insieme al quale corrispondono. Siccome b corrisponde a B, b non può stare in B. Perfetto, ho la risposta: b non appartiene a B”.
“Ma l'insieme B non dovrebbe contenere tutti gli elementi che non appartengono all'insieme a cui sono associati?”.
“Certo”.
“E b non è associato a B?”.
“Certo”.
“Allora b appartiene a B”.
“Certo. No, un momento, ho appena detto che b non appartiene a B. Ora tu mi dici che proprio perché b non appartiene a B allora deve appartenere a B! Mi sembra il paradosso del barbiere”.
“È lui. Osserva che puoi anche partire dalla supposizione contraria: se b appartiene a B significa che b non appartiene all'insieme a cui corrisponde, che è sempre B. Da qualunque parte tu la guardi, è una contraddizione. Se supponi che esista una corrispondenza biunivoca tra A e P(A) arrivi al paradosso, anzi, all'antinomia, del barbiere. E questo non può succedere”.
“Quindi?”.
“Quindi la nostra fantomatica μ non esiste”.
“Wow”.
“E quindi A e P(A) non hanno la stessa cardinalità”.
“Vero”.
“E siccome P(A) contiene A, la cardinalità di P(A) è maggiore di quella di A”.
“Come dicono i giovani d'oggi, il barbiere spakka”.
“Guai a te se scrivi un'altra volta con le k”.
“Ehm”.
Abbiamo visto che se la cardinalità dell'insieme A è α allora la cardinalità dell'insieme delle parti P(A) è 2α. Nel caso in cui α è transfinito, la scrittura 2α è soltanto un simbolo. Ora vogliamo dimostrare che 2α è effettivamente maggiore di α anche nel caso transfinito.
Supponiamo per assurdo che esista una funzione biunivoca μ tra A e P(A).
“Ehm, per assurdo?”.
“Sì, è una tecnica di dimostrazione”.
“Uhm”.
“Funziona così: tu supponi che quello che vuoi dimostrare non sia vero, e provi a vedere cosa succede. Se arrivi a una contraddizione, vuol dire che la tua supposizione iniziale è sbagliata, e quindi quello che vuoi dimostrare è proprio vero”.
“Ah. Un metodo un po' strano, ma credo di aver capito. Prova ad andare avanti”.
“Allora, questa fantomatica corrispondenza biunivoca μ dovrebbe far corrispondere elementi di A a sottoinsiemi di A”.
“Giusto: parte da A (che contiene elementi di A, evidentemente) e arriva a P(A) (che contiene sottoinsiemi di A)”.
“Allora, prendiamo un generico elemento di A e chiamiamolo (con grande fantasia) a”.
“I Veri Matematici sono noti per la loro fantasia”.
“È vero. Un mio prof all'università un giorno ci fece una dimostrazione in cui si mise a usare un sacco di lettere strane. Scoprimmo solo alla fine che voleva arrivare a usare la variabile ηβ”.
“Mi avvalgo della facoltà di non commentare”.
“Comunque dicevamo dell'elemento a. Questo corrisponderà a un sottoinsieme di A”.
“Sì, certo”.
“Questo sottoinsieme di A potrebbe contenere l'elemento a oppure no”.
“Uhm. Ok. Magari, un esempietto?”.
“Immagina che l'insieme A sia {Pippo, Pluto, Paperino}, e prendiamo un elemento di questo insieme, per esempio Pippo. A questo elemento corrisponde un sottoinsieme di A, diciamo che sia {Pluto, Paperino}”.
“Ok. In questo caso a non appartiene al corrispondente insieme”.
“Esatto. Se invece prendo Pluto, e immagino che sia associato a {Pippo, Pluto}, allora vedo che a appartiene al corrispondente insieme”.
“Ok, ci sono, ho capito. Tutti gli elementi di A saranno associati a insiemi, e abbiamo due possibilità: o questi insiemi contengono i corrispondenti elementi, oppure non li contengono”.
“Perfetto. Allora possiamo considerare l'insieme di tutti gli elementi di A che non appartengono al corrispondente insieme, come il Pippo dell'esempio precedente”.
“Ok. Immagino che un Vero Matematico lo chiamerebbe B”.
“Vedo che sei sulla buona strada. Ora, attento: anche B è un sottoinsieme di A, vero?”.
“Certo. Contiene solo elementi di A”.
“E quindi questo B, nella nostra fantomatica corrispondenza biunivoca, proviene da un qualche elemento di A”.
“Sì, se immaginiamo che questa corrispondenza biunivoca esista, come hai detto tu, allora B proviene da... possiamo chiamarlo b?”.
“Certo, un'ottima scelta. L'elemento b è associato a B. Ora arriva la domanda: b appartiene a B?”.
“Vediamo: B contiene solo elementi che non appartengono all'insieme al quale corrispondono. Siccome b corrisponde a B, b non può stare in B. Perfetto, ho la risposta: b non appartiene a B”.
“Ma l'insieme B non dovrebbe contenere tutti gli elementi che non appartengono all'insieme a cui sono associati?”.
“Certo”.
“E b non è associato a B?”.
“Certo”.
“Allora b appartiene a B”.
“Certo. No, un momento, ho appena detto che b non appartiene a B. Ora tu mi dici che proprio perché b non appartiene a B allora deve appartenere a B! Mi sembra il paradosso del barbiere”.
“È lui. Osserva che puoi anche partire dalla supposizione contraria: se b appartiene a B significa che b non appartiene all'insieme a cui corrisponde, che è sempre B. Da qualunque parte tu la guardi, è una contraddizione. Se supponi che esista una corrispondenza biunivoca tra A e P(A) arrivi al paradosso, anzi, all'antinomia, del barbiere. E questo non può succedere”.
“Quindi?”.
“Quindi la nostra fantomatica μ non esiste”.
“Wow”.
“E quindi A e P(A) non hanno la stessa cardinalità”.
“Vero”.
“E siccome P(A) contiene A, la cardinalità di P(A) è maggiore di quella di A”.
“Come dicono i giovani d'oggi, il barbiere spakka”.
“Guai a te se scrivi un'altra volta con le k”.
“Ehm”.
mercoledì 17 settembre 2008
Verso l'infinito, ma con calma - la cardinalità dell'insieme delle parti
Ora andiamo sul difficile, vogliamo dimostrare che se la cardinalità di un insieme A è uguale a α, allora la cardinalità del suo insieme delle parti P(A) è uguale a 2α.
La dimostrazione segue questa strada: si vuole far vedere che l'insieme delle funzioni che vanno da A nell'insieme {0,1} è in corrispondenza biunivoca con P(A).
“Insieme di funzioni? Ma le funzioni sono particolari relazioni, cioè a loro volta sono insiemi. Mi sa che stiamo astraendo troppo”.
“L'avevo detto che era difficile. Proviamo a ragionare con un esempio: immagina di avere davanti a te tutti gli oggetti che fanno parte di A”.
“Va bene. Finiti o infiniti?”.
“Per adesso non importa. Per comodità, pensa che siano finiti, ma non è indispensabile”.
“Ok. Ora che faccio?”.
“Ora immagina che a ogni oggetto sia associata una lampadina, che tu puoi accendere o spegnere a tuo piacimento”.
“Bene, fin qua è facile”.
“Ora pensa di accendere qualche lampadina, quelle che vuoi tu, come vuoi tu”.
“Fatto”.
“Perfetto. Hai associato a ogni elemento di A una lampadina, accesa o spenta”.
“Vero”.
“Se la lampadina accesa rappresenta un 1, e la lampadina spenta rappresenta uno 0, hai associato a ogni elemento di A uno 0 oppure un 1”.
“Ho capito! Ho costruito una funzione che va da A all'insieme {0,1}”.
“Bene. Ora ascolta: in quanti modi puoi creare una sequenza di lampadine accese o spente associate agli elementi di A? Supponiamo per ora che A sia finito”.
“Questa è difficile”.
“No, ragiona in questo modo: per quanto riguarda la prima lampadina, quante possibilità hai?”.
“Beh, 2, o è accesa o spenta”.
“Per quanto riguarda la seconda?”.
“Ancora 2”.
“Quindi, se metti insieme la prima e la seconda lampadina, hai 2 possibilità per la prima, e per ognuna di queste 2 possibilità ne hai altre 2 per la seconda”.
“Totale 4?”.
“Certo. Se vuoi te le elenco: 00, 01, 10, 11”.
“Mh, mi ricorda la numerazione binaria. Se aggiungo una terza lampadina, allora, potrei avere uno 0 da associare a queste quattro possibilità, oppure un 1. Otterrei 000, 001, 010, 011 e poi 100, 101, 110, 111. Totale 8. Ogni volta che aggiungo una lampadina moltiplico per 2!”.
“Bene, quindi se in A ci sono α elementi, hai 2α modi di accendere le lampadine. E cioè, hai 2α funzioni che vanno da A a {0,1}”.
“Ok, ho capito, detto così non è difficile”.
“La matematica non è mai difficile quando la capisci”.
“Permettimi di non commentare e andiamo avanti”.
“Ora vogliamo dimostrare che questo insieme di funzioni è in corrispondenza biunivoca con P(A)”.
“E come facciamo?”.
“Facciamo così: ad ogni successione di lampadine (cioè ad ogni funzione) associamo l'insieme che contiene solo gli elementi per le quali le lampadine sono accese”.
“Credo di aver capito, ma se ci fosse un esempio sarebbe meglio”.
“Va bene. Prendiamo un insieme facile: {a,b}. Ora costruisci tu tutte le funzioni che vanno da questo insieme a {0,1}”.
“Allora, posso associare a a 0 e b a 0. Oppure a a 0 e b a 1. Forse è meglio se faccio uno schema. Eccolo qua, ho numerato le quattro funzioni”.
“Perfetto. Ora scegline una”.
“La numero 2. Era il voto preferito del mio prof di matematica”.
“Va bene. La funzione f2 accende solo una lampadina, quella di b. Quindi ad essa associamo l'insieme {b}”.
“Mh. Forse ho capito. La funzione f1 è associata all'insieme vuoto, perché non accende lampadine?”.
“Giusto. Provi a fare uno schema anche per questa corrispondenza tra funzioni e insiemi?”.
“Ok, ecco qua:”.
“Molto bene. Hai notato che hai elencato tutti i sottoinsiemi dell'insieme da cui siamo partiti, cioé {a,b}?”.
“Vedo. Ma siamo sicuri che non sia un caso?”.
“No, è vero in generale: se prendi due modi diversi di accendere le lampadine, troverai certamente due insiemi diversi. Viceversa, se prendi due insiemi diversi, essi ti daranno modi diversi di accendere le lampadine. Insomma, le lampadine accese corrispondono agli elementi: stesse lampadine, stessi elementi; stessi elementi, stesse lampadine”.
“Va bene”.
“E tieni presente che questa dimostrazione vale anche per il caso infinito. Cioè, puoi mettere in corrispondenza biunivoca i due insiemi delle funzioni da A in {0,1} e P(A) anche se A è infinito. Chiaramente non potrai calcolare 2α in questo caso. Però si può dimostrare che il cardinale transfinito α è minore del cardinale transfinito 2α”.
“Non me lo lasci come esercizio, vero?”.
“No, questo è difficile. Lo vediamo la prossima volta”.
La dimostrazione segue questa strada: si vuole far vedere che l'insieme delle funzioni che vanno da A nell'insieme {0,1} è in corrispondenza biunivoca con P(A).
“Insieme di funzioni? Ma le funzioni sono particolari relazioni, cioè a loro volta sono insiemi. Mi sa che stiamo astraendo troppo”.
“L'avevo detto che era difficile. Proviamo a ragionare con un esempio: immagina di avere davanti a te tutti gli oggetti che fanno parte di A”.
“Va bene. Finiti o infiniti?”.
“Per adesso non importa. Per comodità, pensa che siano finiti, ma non è indispensabile”.
“Ok. Ora che faccio?”.
“Ora immagina che a ogni oggetto sia associata una lampadina, che tu puoi accendere o spegnere a tuo piacimento”.
“Bene, fin qua è facile”.
“Ora pensa di accendere qualche lampadina, quelle che vuoi tu, come vuoi tu”.
“Fatto”.
“Perfetto. Hai associato a ogni elemento di A una lampadina, accesa o spenta”.
“Vero”.
“Se la lampadina accesa rappresenta un 1, e la lampadina spenta rappresenta uno 0, hai associato a ogni elemento di A uno 0 oppure un 1”.
“Ho capito! Ho costruito una funzione che va da A all'insieme {0,1}”.
“Bene. Ora ascolta: in quanti modi puoi creare una sequenza di lampadine accese o spente associate agli elementi di A? Supponiamo per ora che A sia finito”.
“Questa è difficile”.
“No, ragiona in questo modo: per quanto riguarda la prima lampadina, quante possibilità hai?”.
“Beh, 2, o è accesa o spenta”.
“Per quanto riguarda la seconda?”.
“Ancora 2”.
“Quindi, se metti insieme la prima e la seconda lampadina, hai 2 possibilità per la prima, e per ognuna di queste 2 possibilità ne hai altre 2 per la seconda”.
“Totale 4?”.
“Certo. Se vuoi te le elenco: 00, 01, 10, 11”.
“Mh, mi ricorda la numerazione binaria. Se aggiungo una terza lampadina, allora, potrei avere uno 0 da associare a queste quattro possibilità, oppure un 1. Otterrei 000, 001, 010, 011 e poi 100, 101, 110, 111. Totale 8. Ogni volta che aggiungo una lampadina moltiplico per 2!”.
“Bene, quindi se in A ci sono α elementi, hai 2α modi di accendere le lampadine. E cioè, hai 2α funzioni che vanno da A a {0,1}”.
“Ok, ho capito, detto così non è difficile”.
“La matematica non è mai difficile quando la capisci”.
“Permettimi di non commentare e andiamo avanti”.
“Ora vogliamo dimostrare che questo insieme di funzioni è in corrispondenza biunivoca con P(A)”.
“E come facciamo?”.
“Facciamo così: ad ogni successione di lampadine (cioè ad ogni funzione) associamo l'insieme che contiene solo gli elementi per le quali le lampadine sono accese”.
“Credo di aver capito, ma se ci fosse un esempio sarebbe meglio”.
“Va bene. Prendiamo un insieme facile: {a,b}. Ora costruisci tu tutte le funzioni che vanno da questo insieme a {0,1}”.
“Allora, posso associare a a 0 e b a 0. Oppure a a 0 e b a 1. Forse è meglio se faccio uno schema. Eccolo qua, ho numerato le quattro funzioni”.
f1 f2 f3 f4 a-0 a-0 a-1 a-1 b-0 b-1 b-0 b-1
“Perfetto. Ora scegline una”.
“La numero 2. Era il voto preferito del mio prof di matematica”.
“Va bene. La funzione f2 accende solo una lampadina, quella di b. Quindi ad essa associamo l'insieme {b}”.
“Mh. Forse ho capito. La funzione f1 è associata all'insieme vuoto, perché non accende lampadine?”.
“Giusto. Provi a fare uno schema anche per questa corrispondenza tra funzioni e insiemi?”.
“Ok, ecco qua:”.
f1 - {}
f2 - {b}
f3 - {a}
f4 - {a,b}
“Molto bene. Hai notato che hai elencato tutti i sottoinsiemi dell'insieme da cui siamo partiti, cioé {a,b}?”.
“Vedo. Ma siamo sicuri che non sia un caso?”.
“No, è vero in generale: se prendi due modi diversi di accendere le lampadine, troverai certamente due insiemi diversi. Viceversa, se prendi due insiemi diversi, essi ti daranno modi diversi di accendere le lampadine. Insomma, le lampadine accese corrispondono agli elementi: stesse lampadine, stessi elementi; stessi elementi, stesse lampadine”.
“Va bene”.
“E tieni presente che questa dimostrazione vale anche per il caso infinito. Cioè, puoi mettere in corrispondenza biunivoca i due insiemi delle funzioni da A in {0,1} e P(A) anche se A è infinito. Chiaramente non potrai calcolare 2α in questo caso. Però si può dimostrare che il cardinale transfinito α è minore del cardinale transfinito 2α”.
“Non me lo lasci come esercizio, vero?”.
“No, questo è difficile. Lo vediamo la prossima volta”.
martedì 16 settembre 2008
Potevate anche dire qualcosa
Il 23 agosto è stato scoperto il quarantacinquesimo numero primo di Mersenne, 243112609-1, un numero di 12978189 cifre, che si guadagna pure il premio di centomila dollari offerto dalla EFF.
Il 6 settembre ne viene scoperto un altro, il quarantaseiesimo, che però è più piccolo del precedente (anche se supera il milione di cifre e quindi sarebbe stato anch'esso un candidato al premio): 237156667-1.
Il 6 settembre ne viene scoperto un altro, il quarantaseiesimo, che però è più piccolo del precedente (anche se supera il milione di cifre e quindi sarebbe stato anch'esso un candidato al premio): 237156667-1.
Verso l'infinito, ma con calma - l'insieme delle parti
Per salire verso cardinalità sempre più grandi dobbiamo introdurre un nuovo oggetto: l'insieme delle parti. La definizione è semplice: si chiama insieme delle parti di un insieme A l'insieme che contiene tutti i sottoinsiemi di A. Il suo simbolo è P(A) (in realtà la P andrebbe scritta in corsivo, ma non stiamo a sottilizzare).
“Facciamo qualche esempio?”.
“Ok, partiamo dall'insieme più semplice: l'insieme vuoto. L'insieme delle parti è...”.
“Vuoto pure lui”.
“No. L'insieme delle parti contiene un elemento, l'insieme vuoto”.
“Eeeh?”.
“Prova a pensare a cosa significa sottoinsieme”.
“Un sottoinsieme S di A contiene alcuni elementi dell'insieme A”.
“Circa. La definizione corretta è: se x appartiene a S, allora x appartiene anche ad A”.
“Va bene. Possiamo dire che tutti gli elementi di S sono contenuti in A?”.
“Certo. Allora vedi che l'insieme vuoto è sottoinsieme dell'insieme vuoto”.
“Veramente non vedo un bel niente”.
“È vero o no che tutti gli elementi dell'insieme vuoto sono contenuti nell'insieme vuoto, o in qualunque altro insieme?”.
“Ma l'insieme vuoto non ha elementi!”.
“Appunto. Esiste forse qualche elemento dell'insieme vuoto che non è contenuto in qualche insieme?”.
“No, certo, non esistono proprio elementi”.
“Dunque è vero il contrario, tutti gli elementi dell'insieme vuoto sono contenuti in qualunque insieme”.
“Mamma mia, che sofismi. Va bene, ho capito: se A=∅, allora P(A)={∅}”.
“Perfetto. Parlando di cardinalità, Card(∅)=0, Card(P(A))=1”.
“Ok. Possiamo prendere un insieme un pochino più grosso?”.
“Prendiamo A={a}. Quali sono i suoi sottoinsiemi?”.
“Allora, ho capito che c'è l'insieme vuoto, quello è dappertutto”.
“Poi?”.
“Ce ne sono ancora?”.
“Sì”.
“Forse A stesso?”.
“Molto bene: ogni insieme è sottoinsieme di sé stesso. È un concetto analogo a quello di essere minore o uguale tra due numeri. Accettiamo anche l'uguaglianza”.
“Ho capito. Quindi, se A={a}, P(A)={∅,{a}}”.
“Parlando di cardinalità: Card(A)=1, Card(P(A))=2”.
“Ok, ora provo con un insieme di due elementi: A={a,b}. Se non sbaglio, P(A)={∅,{a},{b},{a,b}}. Card(A)=2, Card(P(A))=4”.
“Bene. Facciamo un ultimo esempio con tre elementi: A={a,b,c}. L'insieme delle parti è fatto in questo modo:
P(A)={∅,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}.
Quindi Card(A)=3, mentre Card(P(A))=8”.
“Uhm, mi pare che ci sia una regola sotto”.
“Quale?”.
“Se la cardinalità di A è uguale a n, la cardinalità di P(A) è uguale a 2n”.
“È vero”.
“E si dimostra?”.
“Certo. Per gli insiemi finiti è semplice, per quelli infiniti più complicato, ma la formula vale sempre”.
“Cioè, mi stai dicendo che si può calcolare 2ℵ0?”.
“Già”.
“E immagino che faccia sempre ℵ0?”.
“No. Questa volta fa di più”.
“Ah, quanto?”.
“c gotico”.
“Eh?”.
“I Veri Matematici scrivono una lettera c minuscola in caratteri gotici”.
“Cioè, mi stai dicendo che prima vanno a scomodare l'alfabeto ebraico, prendono la prima lettera e ci aggiungono un indice, come a dire state a vedere quanti numeri tiriamo fuori, poi per un po' temono che quella sia l'unica lettera che mai useranno, e alla fine, quando scoprono che ne possono usare un'altra, scrivono c gotico?”.
“Ehm”.
“Facciamo qualche esempio?”.
“Ok, partiamo dall'insieme più semplice: l'insieme vuoto. L'insieme delle parti è...”.
“Vuoto pure lui”.
“No. L'insieme delle parti contiene un elemento, l'insieme vuoto”.
“Eeeh?”.
“Prova a pensare a cosa significa sottoinsieme”.
“Un sottoinsieme S di A contiene alcuni elementi dell'insieme A”.
“Circa. La definizione corretta è: se x appartiene a S, allora x appartiene anche ad A”.
“Va bene. Possiamo dire che tutti gli elementi di S sono contenuti in A?”.
“Certo. Allora vedi che l'insieme vuoto è sottoinsieme dell'insieme vuoto”.
“Veramente non vedo un bel niente”.
“È vero o no che tutti gli elementi dell'insieme vuoto sono contenuti nell'insieme vuoto, o in qualunque altro insieme?”.
“Ma l'insieme vuoto non ha elementi!”.
“Appunto. Esiste forse qualche elemento dell'insieme vuoto che non è contenuto in qualche insieme?”.
“No, certo, non esistono proprio elementi”.
“Dunque è vero il contrario, tutti gli elementi dell'insieme vuoto sono contenuti in qualunque insieme”.
“Mamma mia, che sofismi. Va bene, ho capito: se A=∅, allora P(A)={∅}”.
“Perfetto. Parlando di cardinalità, Card(∅)=0, Card(P(A))=1”.
“Ok. Possiamo prendere un insieme un pochino più grosso?”.
“Prendiamo A={a}. Quali sono i suoi sottoinsiemi?”.
“Allora, ho capito che c'è l'insieme vuoto, quello è dappertutto”.
“Poi?”.
“Ce ne sono ancora?”.
“Sì”.
“Forse A stesso?”.
“Molto bene: ogni insieme è sottoinsieme di sé stesso. È un concetto analogo a quello di essere minore o uguale tra due numeri. Accettiamo anche l'uguaglianza”.
“Ho capito. Quindi, se A={a}, P(A)={∅,{a}}”.
“Parlando di cardinalità: Card(A)=1, Card(P(A))=2”.
“Ok, ora provo con un insieme di due elementi: A={a,b}. Se non sbaglio, P(A)={∅,{a},{b},{a,b}}. Card(A)=2, Card(P(A))=4”.
“Bene. Facciamo un ultimo esempio con tre elementi: A={a,b,c}. L'insieme delle parti è fatto in questo modo:
P(A)={∅,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}.
Quindi Card(A)=3, mentre Card(P(A))=8”.
“Uhm, mi pare che ci sia una regola sotto”.
“Quale?”.
“Se la cardinalità di A è uguale a n, la cardinalità di P(A) è uguale a 2n”.
“È vero”.
“E si dimostra?”.
“Certo. Per gli insiemi finiti è semplice, per quelli infiniti più complicato, ma la formula vale sempre”.
“Cioè, mi stai dicendo che si può calcolare 2ℵ0?”.
“Già”.
“E immagino che faccia sempre ℵ0?”.
“No. Questa volta fa di più”.
“Ah, quanto?”.
“c gotico”.
“Eh?”.
“I Veri Matematici scrivono una lettera c minuscola in caratteri gotici”.
“Cioè, mi stai dicendo che prima vanno a scomodare l'alfabeto ebraico, prendono la prima lettera e ci aggiungono un indice, come a dire state a vedere quanti numeri tiriamo fuori, poi per un po' temono che quella sia l'unica lettera che mai useranno, e alla fine, quando scoprono che ne possono usare un'altra, scrivono c gotico?”.
“Ehm”.
lunedì 15 settembre 2008
Verso l'infinito, ma con calma - cominciamo dal basso
Abbiamo capito che ℵ0 è il cardinale associato ai numeri naturali. Ora la domanda è questa: esistono cardinali transfiniti più piccoli?
Prendiamo un insieme A, infinito. Da esso scegliamo un elemento, e associamolo al numero 1. Poi ne prendiamo un secondo, e lo associamo al numero 2. Poi un terzo, che associamo a 3, un quarto, e così via. Non c'è mai il pericolo di non trovare un altro elemento, perché A è infinito, e quindi possiamo procedere quanto vogliamo.
In pratica abbiamo costruito una funzione che immerge tutti i numeri naturali all'interno del nostro insieme A (facciamo attenzione perché a una prima lettura potrebbe sembrare il contrario: tutti i numeri naturali vengono associati a infiniti elementi di A, ma non è detto che tutti gli elementi di A vengano presi in considerazione): questo significa che la cardinalità di A sarà maggiore o uguale alla cardinalità dei numeri naturali.
Dunque ℵ0 è il più piccolo cardinale transfinito.
“Bè, questa mi sembra semplice, l'ho capita subito”.
“Purtroppo non è così semplice”.
“Ma come? Una volta che avevo capito!”.
“Il grosso problema è la frase da esso scegliamo un elemento”.
“Oh bella, e perché”.
“Perché scegliere un elemento tra infiniti non è immediato”.
“Ma va? Ce ne sono tanti, potrò pur sceglierne uno!”.
“Mettiamola così: scegliere un elemento tra tanti significa definire una funzione che i Veri Matematici chiamano funzione di scelta. Dato un insieme, la funzione mi dice quale elemento estrarre”.
“Va bene, se ti vuoi complicare la vita, ok”.
“Il problema è che questa funzione non sempre puoi definirla, magari puoi dire che esiste, ma se io ti domando come funziona, quale elemento restituisce, tu non puoi saperlo”.
“Boh?”.
“Ti faccio un esempio: hai presente la corriera con infiniti posti che è arrivata all'albergo di Hilbert?”.
“Sì, me la ricordo”.
“Ok. I passeggeri, stanchi per il viaggio, si sono tolti le scarpe”.
“Che puzza!”.
“E le calze. E hanno appoggiato tutto sopra al loro seggiolino”.
“Bleah”.
“Ora tu devi fare una corsa sulla corriera e portarmi una scarpa per ogni passeggero. Ce la fai?”.
“Mah, sì, tempo permettendo. Ci sono due scarpe, ne prendo una”.
“Quale prendi? Serve una regola”.
“No so, prendo la destra, va bene?”.
“Va bene, avresti potuto prendere la sinistra, oppure stabilire una regola più complicata. Che so, nei seggiolini di posto pari prendo la destra, in quelli di posto dispari la sinistra. Va bene qualunque regola”.
“Mah. Quindi la scelta posso farla”.
“Certo. Ora devi fare un altro giro e prendere una calza per ogni passeggero. Ricordati che le calze possono essere indifferentemente portate nel piede destro oppure nel piede sinistro”.
“Vabbè, ne prendo una”.
“Ma quale?”.
“Ma non lo so, una delle due! Ce ne sono due, una a caso. Sarò ben capace di prenderne una?”.
“Sarai anche capace, ma non sei capace di dirmi una regola. Se non sei capace di fare una scelta esplicita, come faccio io a sapere che hai ottenuto tutte le calze che dovevi raccogliere?”.
“Uhm, questi mi sembrano sofismi da filosofi”.
“Allora ti propongo un patto: io mi fido di te, e dico che tu in un qualche modo che non conosco riuscirai a prendere una calza per ogni persona, e tu mi permetti di esplicitare questa possibilità mediante un assioma. Voglio che sia chiaro che hai bisogno di questo assioma (chiamiamolo atto di fiducia) per poter fare la tua scelta”.
“Va bene”.
“Ecco l'assioma, che i Veri Matematici chiamano assioma della scelta: data una famiglia di scatole, ognuna delle quali contenenti almeno un oggetto, è possibile selezionare esattamente un oggetto da ogni scatola, anche se le scatole sono infinite e non esiste nessuna regola per selezionare gli oggetti”.
“Mah, evidentemente i Veri Matematici ci tengono a sottolineare l'ovvio. Mi pare una cosa inutile”.
“Quindi tu lo prenderesti per vero senza pensarci un momento”.
“Certo”.
“Senti, allora che mi dici di quest'altro, che i veri matematici chiamano principio del buon ordinamento: ogni insieme è ordinabile in modo tale che ogni suo sottoinsieme abbia minimo”.
“Mh, non è chiaro”.
“Pensa ai numeri naturali ordinati. Prendi un qualunque sottoinsieme, uno qualsiasi”.
“Boh, vediamo: {5,42,314,2718}”.
“Perfetto. È vero che ha minimo?”.
“Certo, è 5”.
“Bene, hai capito. Questa operazione la puoi fare sempre: prendi un insieme qualunque, lo riordini opportunamente, e ottieni questa proprietà. Ogni sottoinsieme ha minimo. Ti pare un teorema accettabile?”.
“Certo che no. Se prendo i numeri reali, come faccio a riordinarli in modo tale che ogni sottoinsieme abbia minimo?”.
“Devo dire che hai scelto un ottimo esempio. Nessuno, finora, è riuscito a trovare un ordinamento dei numeri reali con quella proprietà”.
“Dunque il tuo principio del buon ordinamento è falso!”.
“Invece no, è vero”.
“Eh?”.
“Anzi, si dimostra che è equivalente all'assioma della scelta, quello che tu consideravi tanto ovvio”.
“Equivalente?”.
“Sì, se è vero uno, è vero l'altro. Se è falso uno, è falso l'altro. Vanno via in parallelo”.
“Ohi ohi”.
“Oppure prendi quest'altro esempio: è possibile prendere una sfera piena, spezzettarla in piccole parti e poi ricomporle fino ad ottenere due copie identiche della sfera iniziale”.
“Ma va, via, non è possibile”.
“Si chiama paradosso di Banach-Tarski, è tutto vero, e dipende anche questo dal tuo assioma della scelta”.
“Mi gira la testa... Ma i Veri Matematici come prendono queste cose paradossali?”.
“Dipende. Alcuni prima cercano conseguenze dell'assioma della scelta, o enunciati equivalenti tipo il lemma di Zorn, che non sto nemmeno a raccontarti perché dice cose abbastanza incomprensibili”.
“E poi?”.
“Poi ci scherzano sopra, con frasi del tipo l’assioma della scelta è ovviamente vero, il principio del buon ordinamento è ovviamente falso e, circa il lemma di Zorn, chi è capace di capirci qualcosa? Oppure fanno battute sul fatto che tre enunciati equivalenti sono chiamati uno assioma, il secondo principio, il terzo lemma”.
“Carini. E gli altri matematici cosa fanno?”.
“Devo proprio dirtelo?”.
“Ah, ok, ho capito”.
Prendiamo un insieme A, infinito. Da esso scegliamo un elemento, e associamolo al numero 1. Poi ne prendiamo un secondo, e lo associamo al numero 2. Poi un terzo, che associamo a 3, un quarto, e così via. Non c'è mai il pericolo di non trovare un altro elemento, perché A è infinito, e quindi possiamo procedere quanto vogliamo.
In pratica abbiamo costruito una funzione che immerge tutti i numeri naturali all'interno del nostro insieme A (facciamo attenzione perché a una prima lettura potrebbe sembrare il contrario: tutti i numeri naturali vengono associati a infiniti elementi di A, ma non è detto che tutti gli elementi di A vengano presi in considerazione): questo significa che la cardinalità di A sarà maggiore o uguale alla cardinalità dei numeri naturali.
Dunque ℵ0 è il più piccolo cardinale transfinito.
“Bè, questa mi sembra semplice, l'ho capita subito”.
“Purtroppo non è così semplice”.
“Ma come? Una volta che avevo capito!”.
“Il grosso problema è la frase da esso scegliamo un elemento”.
“Oh bella, e perché”.
“Perché scegliere un elemento tra infiniti non è immediato”.
“Ma va? Ce ne sono tanti, potrò pur sceglierne uno!”.
“Mettiamola così: scegliere un elemento tra tanti significa definire una funzione che i Veri Matematici chiamano funzione di scelta. Dato un insieme, la funzione mi dice quale elemento estrarre”.
“Va bene, se ti vuoi complicare la vita, ok”.
“Il problema è che questa funzione non sempre puoi definirla, magari puoi dire che esiste, ma se io ti domando come funziona, quale elemento restituisce, tu non puoi saperlo”.
“Boh?”.
“Ti faccio un esempio: hai presente la corriera con infiniti posti che è arrivata all'albergo di Hilbert?”.
“Sì, me la ricordo”.
“Ok. I passeggeri, stanchi per il viaggio, si sono tolti le scarpe”.
“Che puzza!”.
“E le calze. E hanno appoggiato tutto sopra al loro seggiolino”.
“Bleah”.
“Ora tu devi fare una corsa sulla corriera e portarmi una scarpa per ogni passeggero. Ce la fai?”.
“Mah, sì, tempo permettendo. Ci sono due scarpe, ne prendo una”.
“Quale prendi? Serve una regola”.
“No so, prendo la destra, va bene?”.
“Va bene, avresti potuto prendere la sinistra, oppure stabilire una regola più complicata. Che so, nei seggiolini di posto pari prendo la destra, in quelli di posto dispari la sinistra. Va bene qualunque regola”.
“Mah. Quindi la scelta posso farla”.
“Certo. Ora devi fare un altro giro e prendere una calza per ogni passeggero. Ricordati che le calze possono essere indifferentemente portate nel piede destro oppure nel piede sinistro”.
“Vabbè, ne prendo una”.
“Ma quale?”.
“Ma non lo so, una delle due! Ce ne sono due, una a caso. Sarò ben capace di prenderne una?”.
“Sarai anche capace, ma non sei capace di dirmi una regola. Se non sei capace di fare una scelta esplicita, come faccio io a sapere che hai ottenuto tutte le calze che dovevi raccogliere?”.
“Uhm, questi mi sembrano sofismi da filosofi”.
“Allora ti propongo un patto: io mi fido di te, e dico che tu in un qualche modo che non conosco riuscirai a prendere una calza per ogni persona, e tu mi permetti di esplicitare questa possibilità mediante un assioma. Voglio che sia chiaro che hai bisogno di questo assioma (chiamiamolo atto di fiducia) per poter fare la tua scelta”.
“Va bene”.
“Ecco l'assioma, che i Veri Matematici chiamano assioma della scelta: data una famiglia di scatole, ognuna delle quali contenenti almeno un oggetto, è possibile selezionare esattamente un oggetto da ogni scatola, anche se le scatole sono infinite e non esiste nessuna regola per selezionare gli oggetti”.
“Mah, evidentemente i Veri Matematici ci tengono a sottolineare l'ovvio. Mi pare una cosa inutile”.
“Quindi tu lo prenderesti per vero senza pensarci un momento”.
“Certo”.
“Senti, allora che mi dici di quest'altro, che i veri matematici chiamano principio del buon ordinamento: ogni insieme è ordinabile in modo tale che ogni suo sottoinsieme abbia minimo”.
“Mh, non è chiaro”.
“Pensa ai numeri naturali ordinati. Prendi un qualunque sottoinsieme, uno qualsiasi”.
“Boh, vediamo: {5,42,314,2718}”.
“Perfetto. È vero che ha minimo?”.
“Certo, è 5”.
“Bene, hai capito. Questa operazione la puoi fare sempre: prendi un insieme qualunque, lo riordini opportunamente, e ottieni questa proprietà. Ogni sottoinsieme ha minimo. Ti pare un teorema accettabile?”.
“Certo che no. Se prendo i numeri reali, come faccio a riordinarli in modo tale che ogni sottoinsieme abbia minimo?”.
“Devo dire che hai scelto un ottimo esempio. Nessuno, finora, è riuscito a trovare un ordinamento dei numeri reali con quella proprietà”.
“Dunque il tuo principio del buon ordinamento è falso!”.
“Invece no, è vero”.
“Eh?”.
“Anzi, si dimostra che è equivalente all'assioma della scelta, quello che tu consideravi tanto ovvio”.
“Equivalente?”.
“Sì, se è vero uno, è vero l'altro. Se è falso uno, è falso l'altro. Vanno via in parallelo”.
“Ohi ohi”.
“Oppure prendi quest'altro esempio: è possibile prendere una sfera piena, spezzettarla in piccole parti e poi ricomporle fino ad ottenere due copie identiche della sfera iniziale”.
“Ma va, via, non è possibile”.
“Si chiama paradosso di Banach-Tarski, è tutto vero, e dipende anche questo dal tuo assioma della scelta”.
“Mi gira la testa... Ma i Veri Matematici come prendono queste cose paradossali?”.
“Dipende. Alcuni prima cercano conseguenze dell'assioma della scelta, o enunciati equivalenti tipo il lemma di Zorn, che non sto nemmeno a raccontarti perché dice cose abbastanza incomprensibili”.
“E poi?”.
“Poi ci scherzano sopra, con frasi del tipo l’assioma della scelta è ovviamente vero, il principio del buon ordinamento è ovviamente falso e, circa il lemma di Zorn, chi è capace di capirci qualcosa? Oppure fanno battute sul fatto che tre enunciati equivalenti sono chiamati uno assioma, il secondo principio, il terzo lemma”.
“Carini. E gli altri matematici cosa fanno?”.
“Devo proprio dirtelo?”.
“Ah, ok, ho capito”.
domenica 14 settembre 2008
Carnevale della Matematica 5
È uscito oggi dai Rudi Matematici, e qua ci pavoneggiamo molto per il buon grado di anticonformismo creativo...
sabato 13 settembre 2008
Verso l'infinito, ma con calma - operazioni con gli alef
Il paradosso dell'albergo di Hilbert ci fa capire che il senso comune non ci aiuta più, quando si tratta di fare operazioni che coinvolgono i cardinali transfiniti.
Nel primo esempio (l'albergo è pieno, arriva un nuovo ospite) abbiamo praticamente visto che ℵ0+1=ℵ0. Non è difficile generalizzare al caso in cui arriva un numero finito n di ospiti. Otterremo sempre che
ℵ0+n=ℵ0.
Nel caso dell'unico nuovo arrivato, abbiamo messo in corrispondenza biunivoca l'insieme degli infiniti ospiti (cioè i numeri naturali) con l'insieme degli infiniti ospiti più uno (cioè i naturali con l'aggiunta di un nuovo elemento). La funzione biunivoca è f(n)=n+1. Esercizio facile: scrivere la funzione biunivoca nel caso in cui arrivi un numero x finito di ospiti.
E fin qua il senso comune potrebbe essere ancora d'accordo: dire che infinito più uno è uguale a infinito non è sconvolgente più di tanto.
Quando arrivano infiniti nuovi ospiti le cose sembrano complicarsi, in realtà l'albergatore se l'è cavata con poco: ha utilizzato la funzione f(n)=2n per liberare infiniti posti. Esercizio facile: scrivere la funzione biunivoca che mette in corrispondenza i due insiemi. In questo caso, allora, abbiamo verificato la formula:
ℵ0+ℵ0=ℵ0.
Nell'ultimo caso arriva un'infinità di infiniti, ma l'albergatore trova posto per tutti (lasciando anche qualche posto vuoto, per eventuali nuovi ospiti. Esercizio: trovare qualche posto vuoto). Abbiamo visto dunque che
ℵ0·ℵ0=ℵ0.
“Insomma, con l'infinito puoi farci quello che vuoi, ma rimane sempre infinito”.
“Eh, no. Non è così, Cantor ha scoperto che ci sono diversi livelli di infinito”.
“Ah. E come ha fatto?”.
“Ha cominciato a mettere in corrispondenza biunivoca insiemi diversi, e ha iniziato a capire come stavano le cose. Per esempio, ha visto che i numeri naturali e i numeri interi sono in corrispondenza biunivoca”.
“Uhm, com'è possibile?”.
“Si può fare così: ai numeri pari puoi associare n/2, ai numeri dispari invece -(n+1)/2”.
“Mh, devo provare. Allora, a 0 associo 0, e fin qua siamo a posto. A 1, che è dispari, associo -1. A 2 associo 1. A 3 associo -2. Ah, vedo. È come se elencassi i numeri interi in questo modo: 0, -1, 1, -2, 2, -3, 3, e così via”.
“Proprio così. Cantor ha visto che i numeri interi, pur sembrando il doppio dei numeri naturali, in realtà sono caratterizzati dallo stesso tipo di infinito”.
“Allora avrà preso i numeri razionali e si sarà accorto che quelli sono di più, giusto?”.
“No, ti sbagli. I numeri razionali, cioè le frazioni, possono essere messi in corrispondenza biunivoca con i naturali”.
“Anche loro? Non riesco a capire come”.
“Cantor ha usato un procedimento ingegnoso. Prima di tutto, ha scritto i razionali come coppie di numeri: numeratore/denominatore. Ha considerato solo quelle positive, ma non è difficile estendere il procedimento anche a quelle negative. Si può sempre usare il metodo dell'albergatore, che ha spostato tutti gli ospiti nelle camere pari”.
“Ok”.
“Poi le ha messe in un tabella, in questo modo”.
“In questo modo ci sono alcuni numeri che si ripetono, però: 1/1 è uguale a 2/2, a 3/3, eccetera”.
“Non importa, perché questi numeri sono di più delle frazioni, e Cantor ha dimostrato che comunque la loro cardinalità è ℵ0”.
“Ah, va bene. Come ha fatto, allora, a dimostrarlo?”.
“Ha fatto vedere un modo per contare le frazioni. Eccolo qua”.
“Geniale! Ha seguito le diagonali! Ma, allora, esistono insiemi con cardinalità maggiore di quella dei numeri naturali?”.
“Questo dubbio è venuto anche a Cantor, in effetti. Si può salire, creando una sorta di graduatoria di numeri transfiniti?”.
“E si può?”.
“Sì, finché vuoi. Ma c'è un'altra domanda non meno importante: si può scendere?”.
“Intendi dire se esistono infiniti, anzi, transfiniti, più piccoli di ℵ0?”.
“Esattamente, ma in questo caso la risposta è no”.
“Oh, bene, una certezza”.
“Se consideri valido l'assioma della scelta”.
“Come?”.
“Niente, niente”.
Nel primo esempio (l'albergo è pieno, arriva un nuovo ospite) abbiamo praticamente visto che ℵ0+1=ℵ0. Non è difficile generalizzare al caso in cui arriva un numero finito n di ospiti. Otterremo sempre che
ℵ0+n=ℵ0.
Nel caso dell'unico nuovo arrivato, abbiamo messo in corrispondenza biunivoca l'insieme degli infiniti ospiti (cioè i numeri naturali) con l'insieme degli infiniti ospiti più uno (cioè i naturali con l'aggiunta di un nuovo elemento). La funzione biunivoca è f(n)=n+1. Esercizio facile: scrivere la funzione biunivoca nel caso in cui arrivi un numero x finito di ospiti.
E fin qua il senso comune potrebbe essere ancora d'accordo: dire che infinito più uno è uguale a infinito non è sconvolgente più di tanto.
Quando arrivano infiniti nuovi ospiti le cose sembrano complicarsi, in realtà l'albergatore se l'è cavata con poco: ha utilizzato la funzione f(n)=2n per liberare infiniti posti. Esercizio facile: scrivere la funzione biunivoca che mette in corrispondenza i due insiemi. In questo caso, allora, abbiamo verificato la formula:
ℵ0+ℵ0=ℵ0.
Nell'ultimo caso arriva un'infinità di infiniti, ma l'albergatore trova posto per tutti (lasciando anche qualche posto vuoto, per eventuali nuovi ospiti. Esercizio: trovare qualche posto vuoto). Abbiamo visto dunque che
ℵ0·ℵ0=ℵ0.
“Insomma, con l'infinito puoi farci quello che vuoi, ma rimane sempre infinito”.
“Eh, no. Non è così, Cantor ha scoperto che ci sono diversi livelli di infinito”.
“Ah. E come ha fatto?”.
“Ha cominciato a mettere in corrispondenza biunivoca insiemi diversi, e ha iniziato a capire come stavano le cose. Per esempio, ha visto che i numeri naturali e i numeri interi sono in corrispondenza biunivoca”.
“Uhm, com'è possibile?”.
“Si può fare così: ai numeri pari puoi associare n/2, ai numeri dispari invece -(n+1)/2”.
“Mh, devo provare. Allora, a 0 associo 0, e fin qua siamo a posto. A 1, che è dispari, associo -1. A 2 associo 1. A 3 associo -2. Ah, vedo. È come se elencassi i numeri interi in questo modo: 0, -1, 1, -2, 2, -3, 3, e così via”.
“Proprio così. Cantor ha visto che i numeri interi, pur sembrando il doppio dei numeri naturali, in realtà sono caratterizzati dallo stesso tipo di infinito”.
“Allora avrà preso i numeri razionali e si sarà accorto che quelli sono di più, giusto?”.
“No, ti sbagli. I numeri razionali, cioè le frazioni, possono essere messi in corrispondenza biunivoca con i naturali”.
“Anche loro? Non riesco a capire come”.
“Cantor ha usato un procedimento ingegnoso. Prima di tutto, ha scritto i razionali come coppie di numeri: numeratore/denominatore. Ha considerato solo quelle positive, ma non è difficile estendere il procedimento anche a quelle negative. Si può sempre usare il metodo dell'albergatore, che ha spostato tutti gli ospiti nelle camere pari”.
“Ok”.
“Poi le ha messe in un tabella, in questo modo”.
1/1 1/2 1/3 ...2/1 2/2 2/3 ...3/1 3/2 3/3 ......
“In questo modo ci sono alcuni numeri che si ripetono, però: 1/1 è uguale a 2/2, a 3/3, eccetera”.
“Non importa, perché questi numeri sono di più delle frazioni, e Cantor ha dimostrato che comunque la loro cardinalità è ℵ0”.
“Ah, va bene. Come ha fatto, allora, a dimostrarlo?”.
“Ha fatto vedere un modo per contare le frazioni. Eccolo qua”.
“Geniale! Ha seguito le diagonali! Ma, allora, esistono insiemi con cardinalità maggiore di quella dei numeri naturali?”.
“Questo dubbio è venuto anche a Cantor, in effetti. Si può salire, creando una sorta di graduatoria di numeri transfiniti?”.
“E si può?”.
“Sì, finché vuoi. Ma c'è un'altra domanda non meno importante: si può scendere?”.
“Intendi dire se esistono infiniti, anzi, transfiniti, più piccoli di ℵ0?”.
“Esattamente, ma in questo caso la risposta è no”.
“Oh, bene, una certezza”.
“Se consideri valido l'assioma della scelta”.
“Come?”.
“Niente, niente”.
venerdì 12 settembre 2008
Verso l'infinito, ma con calma - i paradossi dell'infinito
L'albergo Hilbert è un albergo molto particolare: ha infinite stanze, tutte belle, arieggiate, con bagno e con un'ottima vista. Siamo all'inizio dell'alta stagione, e le stanze sono già tutte occupate.
Un giorno arriva un turista, parcheggia la sua auto nell'ampio parcheggio a fianco dell'albergo, e domanda una stanza. Il portiere controlla per un momento il suo registro, poi attiva il microfono che gli permette di parlare con tutte le stanze, e dice:
“Avvertiamo i nostri gentili ospiti che è necessario un cambio di stanza. Chi si trova nella stanza numero n dovrà spostarsi nella numero n+1”.
Poi, rivolgendosi al nuovo cliente, continua:
“Ecco a lei, signore, la chiave della sua stanza. È la numero 0”.
Il giorno dopo arriva, in corriera, una comitiva numerosa. Il capo gita scende velocemente e va dall'albergatore, per chiedere se c'è posto per tutti.
“Quanti siete?”.
“Infiniti”.
“Ah, però. Un momento solo”, e, parlando di nuovo al microfono, si rivolge ai suoi clienti: “si comunica ai gentili ospiti che è necessario un cambio di stanza. Chi si trova alla stanza numero n deve recarsi alla numero 2n, grazie”. Poi, rivolto al capo gita: “Ecco a lei, queste sono le chiavi delle stanze dispari, le può distribuire come crede ai suoi”.
“Molte grazie, avreste ancora un po' di posto per altri ospiti? Dovrebbero arrivare la prossima settimana”.
“Non c'è problema”.
Dopo una settimana, infatti, arriva una lunga serie di corriere. Il responsabile della comitiva scende e va a parlare col portiere, un po' preoccupato alla vista di tanta gente.
“Buongiorno, avete posto per un po' di persone?”.
“Quanti siete?”.
“Bè, in ogni corriera ci sono infinite persone”.
“E quante corriere avete?”.
“Infinite”.
“Pensavo peggio. Certo, certo, c'è posto. Un attimo solo che devo comunicare qualche cambiamento di stanza”. E, nuovamente parlando al microfono: “Ci scusiamo con i gentili ospiti, ma è necessario un cambio di stanza. Chi si trova alla stanza numero n deve recarsi alla numero 2n, grazie”. Poi, consegnando un piccolo visore con alcuni bottoni al responsabile della comitiva: “ecco a lei, tenga. Questo è un generatore di numeri primi. Gli occupanti della prima corriera andranno alle stanze del tipo 3n, quelli della seconda corriera alle stanze del tipo 5n, poi 7n, e così via. Mi raccomando non si sbagli, controlli sempre sul generatore. Una volta è venuta una gita sociale della facoltà di ingegneria e mi hanno occupato tutte le 9n, non le dico le discussioni che ci sono state dopo”.
Un giorno arriva un turista, parcheggia la sua auto nell'ampio parcheggio a fianco dell'albergo, e domanda una stanza. Il portiere controlla per un momento il suo registro, poi attiva il microfono che gli permette di parlare con tutte le stanze, e dice:
“Avvertiamo i nostri gentili ospiti che è necessario un cambio di stanza. Chi si trova nella stanza numero n dovrà spostarsi nella numero n+1”.
Poi, rivolgendosi al nuovo cliente, continua:
“Ecco a lei, signore, la chiave della sua stanza. È la numero 0”.
Il giorno dopo arriva, in corriera, una comitiva numerosa. Il capo gita scende velocemente e va dall'albergatore, per chiedere se c'è posto per tutti.
“Quanti siete?”.
“Infiniti”.
“Ah, però. Un momento solo”, e, parlando di nuovo al microfono, si rivolge ai suoi clienti: “si comunica ai gentili ospiti che è necessario un cambio di stanza. Chi si trova alla stanza numero n deve recarsi alla numero 2n, grazie”. Poi, rivolto al capo gita: “Ecco a lei, queste sono le chiavi delle stanze dispari, le può distribuire come crede ai suoi”.
“Molte grazie, avreste ancora un po' di posto per altri ospiti? Dovrebbero arrivare la prossima settimana”.
“Non c'è problema”.
Dopo una settimana, infatti, arriva una lunga serie di corriere. Il responsabile della comitiva scende e va a parlare col portiere, un po' preoccupato alla vista di tanta gente.
“Buongiorno, avete posto per un po' di persone?”.
“Quanti siete?”.
“Bè, in ogni corriera ci sono infinite persone”.
“E quante corriere avete?”.
“Infinite”.
“Pensavo peggio. Certo, certo, c'è posto. Un attimo solo che devo comunicare qualche cambiamento di stanza”. E, nuovamente parlando al microfono: “Ci scusiamo con i gentili ospiti, ma è necessario un cambio di stanza. Chi si trova alla stanza numero n deve recarsi alla numero 2n, grazie”. Poi, consegnando un piccolo visore con alcuni bottoni al responsabile della comitiva: “ecco a lei, tenga. Questo è un generatore di numeri primi. Gli occupanti della prima corriera andranno alle stanze del tipo 3n, quelli della seconda corriera alle stanze del tipo 5n, poi 7n, e così via. Mi raccomando non si sbagli, controlli sempre sul generatore. Una volta è venuta una gita sociale della facoltà di ingegneria e mi hanno occupato tutte le 9n, non le dico le discussioni che ci sono state dopo”.
giovedì 11 settembre 2008
Verso l'infinito, ma con calma - alef
E finalmente arriviamo a parlare di infinito. Qual è la cardinalità dell'insieme dei numeri naturali? Dato che questo insieme è infinito, la sua cardinalità non sarà un numero, quindi non esiste, fine della storia.
Per fortuna le cose non sono andate così: Cantor è andato avanti, definendo (scoprendo?) nuovi numeri. Alla cardinalità dei numeri naturali ha associato il cardinale transfinito ℵ0 (si legge alef zero, e a volte si trova scritto aleph. Per rendere le cose semplici Cantor ha scelto la prima lettera dell'alfabeto ebraico).
Insomma, tutti gli elementi in corrispondenza biunivoca coi numeri naturali hanno cardinalità uguale a ℵ0: sono cioè infiniti.
“Ma possiamo confrontare questo alef zero con gli altri numeri? Voglio dire, quando si parla di infinito si vorrebbe intendere qualcosa di più grande di tutto il resto. Possiamo dire che alef zero è maggiore di 42, per dire?”.
“Certo che si può: tra i cardinali (di tutti i tipi) si possono fare confronti”.
“Come si fa?”.
“Qui saltano fuori di nuovo le funzioni. Ricordi che avere la stessa cardinalità significa essere in corrispondenza biunivoca?”.
“Sì, una freccia per ogni elemento, nessuno escluso”.
“Perfetto. Ora pensa a una funzione iniettiva da A a B. Iniettiva, ma non suriettiva”.
“Mh, vediamo. Da ogni elemento di A parte una sola freccia”.
“Bene, poi?”.
“Frecce diverse vanno a finire su elementi diversi di B, non si possono congiungere”.
“Ok”.
“Ma non tutti gli elementi di B sono raggiunti”.
“Benissimo. Intuitivamente, B ha più elementi di A”.
“Ok, certo. Tutti gli elementi di A sono associati a B, ma in B ne avanza qualcuno”.
“Bene, questa è la nostra definizione: diciamo che la cardinalità di A è minore della cardinalità di B se esiste una funzione iniettiva ma non suriettiva che va da A a B. In pratica possiamo immergere A dentro a B”.
“Tutto chiaro, bene”.
“Se, poi, sappiamo che la funzione è certamente iniettiva, ma non sappiamo se è anche suriettiva, allora diciamo che la cardinalità di A è minore o uguale a quella di B”.
“D'accordo, se non abbiamo la certezza che avanzino dei termini in B, dobbiamo usare questa formulazione debole”.
“Un modo alternativo per dire che la cardinalità di A è minore di quella di B è questo: le due cardinalità devono essere diverse, e l'insieme A deve essere strettamente contenuto in B”.
“Ma è necessario specificare che le due cardinalità devono essere diverse? Se A è strettamente contenuto in B, allora la cardinalità di A sarà certamente diversa da quella di B”.
“Ecco, ehm, no”.
“No? Ma come è possibile?”.
“Ecco, ci sono concetti che, quando si ha a che fare con l'infinito, sono un po' diversi da quelli che ci aspetteremmo”.
“Paradossi?”.
“Paradossi. Questa volta sono veri paradossi, non antinomie. Se li nominiamo non succede nulla”.
(Esercizio: dimostrare che 42 è minore di ℵ0)
Per fortuna le cose non sono andate così: Cantor è andato avanti, definendo (scoprendo?) nuovi numeri. Alla cardinalità dei numeri naturali ha associato il cardinale transfinito ℵ0 (si legge alef zero, e a volte si trova scritto aleph. Per rendere le cose semplici Cantor ha scelto la prima lettera dell'alfabeto ebraico).
Insomma, tutti gli elementi in corrispondenza biunivoca coi numeri naturali hanno cardinalità uguale a ℵ0: sono cioè infiniti.
“Ma possiamo confrontare questo alef zero con gli altri numeri? Voglio dire, quando si parla di infinito si vorrebbe intendere qualcosa di più grande di tutto il resto. Possiamo dire che alef zero è maggiore di 42, per dire?”.
“Certo che si può: tra i cardinali (di tutti i tipi) si possono fare confronti”.
“Come si fa?”.
“Qui saltano fuori di nuovo le funzioni. Ricordi che avere la stessa cardinalità significa essere in corrispondenza biunivoca?”.
“Sì, una freccia per ogni elemento, nessuno escluso”.
“Perfetto. Ora pensa a una funzione iniettiva da A a B. Iniettiva, ma non suriettiva”.
“Mh, vediamo. Da ogni elemento di A parte una sola freccia”.
“Bene, poi?”.
“Frecce diverse vanno a finire su elementi diversi di B, non si possono congiungere”.
“Ok”.
“Ma non tutti gli elementi di B sono raggiunti”.
“Benissimo. Intuitivamente, B ha più elementi di A”.
“Ok, certo. Tutti gli elementi di A sono associati a B, ma in B ne avanza qualcuno”.
“Bene, questa è la nostra definizione: diciamo che la cardinalità di A è minore della cardinalità di B se esiste una funzione iniettiva ma non suriettiva che va da A a B. In pratica possiamo immergere A dentro a B”.
“Tutto chiaro, bene”.
“Se, poi, sappiamo che la funzione è certamente iniettiva, ma non sappiamo se è anche suriettiva, allora diciamo che la cardinalità di A è minore o uguale a quella di B”.
“D'accordo, se non abbiamo la certezza che avanzino dei termini in B, dobbiamo usare questa formulazione debole”.
“Un modo alternativo per dire che la cardinalità di A è minore di quella di B è questo: le due cardinalità devono essere diverse, e l'insieme A deve essere strettamente contenuto in B”.
“Ma è necessario specificare che le due cardinalità devono essere diverse? Se A è strettamente contenuto in B, allora la cardinalità di A sarà certamente diversa da quella di B”.
“Ecco, ehm, no”.
“No? Ma come è possibile?”.
“Ecco, ci sono concetti che, quando si ha a che fare con l'infinito, sono un po' diversi da quelli che ci aspetteremmo”.
“Paradossi?”.
“Paradossi. Questa volta sono veri paradossi, non antinomie. Se li nominiamo non succede nulla”.
(Esercizio: dimostrare che 42 è minore di ℵ0)
Iscriviti a:
Commenti (Atom)