«Uffa».
«Che riguarda il famoso legame tra le radici e i coefficienti di un'equazione di secondo grado».
«Non ne avevamo già parlato?».
«Sì, ora generalizziamo».
«Andiamo bene».
«Prendiamo un'equazione di grado n, e per comodità facciamo in modo che il coefficiente del termine di grado massimo sia uguale a 1».
«Se non lo è, possiamo sempre dividere tutti i termini per quel valore».
«Proprio così. Scriviamo l'equazione in questo modo: xn+a1xn-1+a2xn-2+…+an = 0».
«Bleah».
«E indichiamo con r1, r2, …, rn le sue radici, eventualmente multiple, eventualmente complesse».
«D'accordo».
«Allora, il teorema dice questo: la somma di tutte le radici è uguale a -a1».
«Come nel caso del secondo grado: avevamo indicato il coefficiente di x con -S, cioè la somma cambiata di segno».
«Giusto, anche se qui non stiamo parlando del coefficiente di x, ma di xn-1».
«Ah, ok».
«Il teorema va avanti, e dà un significato a tutti i coefficienti. Per esempio, la somma di tutti i prodotti del tipo rirj, con i minore di j, è uguale a a2».
«Uhm».
«La somma di tutti i prodotti del tipo rirjrk, con i minore di j e di k, e j minore di k, è uguale a -a3».
«Vedo che questi a hanno i segni alterni, è così sempre, andando avanti?».
«Esatto, i segni sono sempre alterni, e si parte dal segno meno. Ogni coefficiente si ottiene sommando tutti i prodotti ottenuti moltiplicando tra loro due, tre, quattro radici, e così via».
«Alla fine cosa ho?».
«L'ultimo termine è un unico prodotto, di tutte le radici, che è uguale in valore assoluto a an. Il segno dipende dal valore di n: se è pari, il segno è positivo, altrimenti è negativo».
«Ok, non conoscevo questa generalizzazione».
«Infatti, a scuola non si spiega. Finalmente siamo pronti per vedere un esempio concreto, il pentagono».
«Oh, bene».
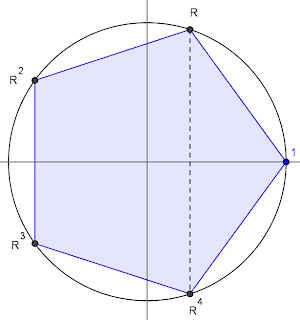
«Per prima cosa, rappresentiamo le radici dell'equazione x5-1 = 0 in questo modo: 1, R, R2, R3, R4».
«Ricordo che avevamo parlato di questa notazione. Avevi anche detto che queste radici formano un gruppo».
«Ottimo. Ora le accoppiamo in questo modo:».
y1 = R+R4,
y2 = R2+R3.
«Perché in questo modo?».
«Osserva la figura: gli accoppiamenti sono fatti tra radici che hanno la stessa parte reale, e parte immaginaria opposta».
«Sono radici complesse coniugate, vero?».
«Esatto, si chiamano così. Se le sommi, sparisce la parte immaginaria e rimangono solo numeri reali».
«Ah, ecco. Quindi i nostri y sono numeri reali, bene».
«Ora prova a calcolare la somma y1+y2».
«Dovrebbe risultare R+R4+R2+R3».
«Quanto fa?».
«Boh, come faccio a saperlo?».
«Guarda quello che hai sommato: sono tutte le radici dell'equazione iniziale, tranne quella uguale a 1».
«E quindi?».
«E quindi sono le soluzioni dell'equazione ciclotomica».
«Non vorrei ripetermi, ma quindi questo a cosa mi serve?».
«Se sostituisci R al posto di x nell'equazione ciclotomica del pentagono, cosa ottieni?».
«Uhm, viene R4+R3+R2+R+1 = 0. Ehi, ho capito, se porto 1 a destra dell'uguale, ottengo che la somma che voglio calcolare è uguale a -1».
«Molto bene, quindi y1+y2 = -1. Ora prova a calcolare il prodotto y1y2».
«Pronti. Mi viene R3+R4+R6+R7. Non mi piace».
«Ricordati quello che abbiamo detto sulle radici dell'unità. Quanto fa R6?».
«Dovrebbe essere uguale a R, funziona come le lancette dell'orologio, mi ricordo».
«Benissimo. E quanto fa R7?».
«R2. Ma allora il prodotto risulta uguale alla somma, sempre -1».
«Sì. Quindi il nostro problema diventa: trova due numeri y1 e y2 la cui somma sia uguale a -1 e il cui prodotto sia ancora uguale a -1».
«Mi basta la regola delle equazioni di secondo grado, non ho bisogno della tua generalizzazione».
«Per questo esempio, no. Per il prossimo sì: allora, che equazione devi risolvere?».
«Questa: y2+y-1 = 0».
«Che è una equazione irriducibile di secondo grado, quindi possiamo costruire con riga e compasso le sue soluzioni. Da lì, sappiamo trovare tutti gli R, e quindi il pentagono è costruibilie».
«Ma questo lo sapevano fare anche i greci, senza equazioni ciclotomiche».
«Già. E noi, utilizzando un altro metodo più complicato, abbiamo ottenuto lo stesso risultato. Non è meraviglioso che tutto torni?».
«Tu non sei normale».
Nessun commento:
Posta un commento