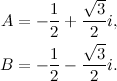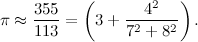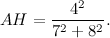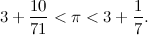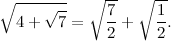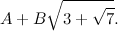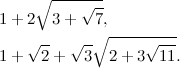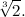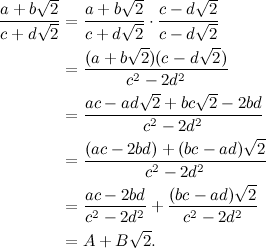I greci non erano normali — 15: radici dell'unità

«Parliamo di radici dell'unità».

«Eh? Ma poi, cosa significa? Radice di uno è uno, fine del problema».

«Eh, magari. Allora, per prima cosa per radice dell'unità si intende qualunque numero che sia soluzione dell'equazione xⁿ = 1. Per essere più precisi, quei numeri si chiamano radici n-esime dell'unità».

«E dai, ma perché usi il plurale? Ah, no, aspetta, ho capito, quando n è un numero pari anche -1 è soluzione dell'equazione. Quando n è dispari però no. Anche se io insisto sul fatto che radice di uno sia uguale a uno, e basta».

«Vero, radice di uno è uno. Ed è anche vero che se n è pari, allora -1 elevato alla n è uguale a 1, ma noi ora ci mettiamo nei numeri complessi».

«Uhm. Quella roba con la i?».

«Esatto».

«Con i² = -1?».

«Proprio quelli. Ti ricordi quando abbiamo esteso i numeri razionali introducendo radici di numeri che non sono quadrati perfetti?».

«Sì, avevamo ad esempio creato numeri del tipo a+b√2».

«Giusto. Ora, quello che si fa per creare i numeri complessi è la stessa cosa: si aggiunge i al campo dei numeri reali, e si ottengono numeri del tipo a+bi».

«Che formano un campo pure loro?».

«Certo, non cambia nulla rispetto a quanto abbiamo detto quando abbiamo esteso i razionali con le radici. Ora utilizziamo uno strumento molto comodo per visualizzare i numeri complessi: il piano complesso».

«Se ben ricordo, è come il piano cartesiano».

«Sì, solo che invece di avere un asse delle x e uno delle y, ha un asse reale e un asse immaginario. Se il numero che vuoi rappresentare è a+bi, allora metti in ascissa a e in ordinata b».

«Come se io volessi rappresentare il punto (a,b)».

«Proprio così. Ora torniamo alle radici n-esime dell'unità: in campo complesso sono sempre n».

«Mh, io ne vedo una sola, al massimo due».

«Per capire come mai ce ne siano n, bisogna che parliamo un momento dei due modi di rappresentare un numero complesso su un piano. Uno è quello che abbiamo detto poco fa, il numero a+bi diventa il punto (a,b)».

«E l'altro?».

«L'altro non usa le coordinate cartesiane, ma quelle polari. Invece di dirti “muoviti in orizzontale di a e in verticale di b”, ti dice “ruota di un certo angolo θ rispetto all'orizzontale e cammina di una certa lunghezza ρ”».

«Ok, mi pare di aver capito. Servono sempre due numeri».

«Sì, i numeri complessi stanno su un piano, quindi servono sempre due numeri per definirli».

«E perché ci piace questa forma polare?».

«Perché gode di una interessante proprietà che riguarda le potenze. Se tu vuoi elevare alla n un certo numero complesso, ti basta elevare alla n la sua lunghezza ρ (che si chiama modulo) e moltiplicare per n il suo angolo θ (che si chiama argomento)».

«Ah, quindi in un certo senso questi numeri ruotano nel piano».

«Sì, esatto. Allora, per fare la radice n-esima, ti basta fare il contrario: fai la radice n-esima del modulo e dividi per n l'argomento».

«E questo mi serve per le radici dell'unità?».

«Sì, ora ti spiego. Per prima cosa, l'unità ha modulo uguale a 1, quindi se la elevi o se ne estrai la radice, il suo modulo rimane tale e quale».

«Ok, fin qua ci sono. Quindi ci rimane da ragionare sulle rotazioni».

«Sì. Partiamo da un esempio semplice: avevi detto che 1 e -1 sono radici quadrate dell'unità».

«Vero».

«Questo significa che se le eleviamo al quadrato, otteniamo 1. Allora, se vogliamo verificare la proprietà che ti ho raccontato prima, dobbiamo rappresentarle sul piano complesso e raddoppiare il loro argomento».

«E fare il quadrato del modulo».

«Ma il modulo è uguale a 1, quindi rimane 1».

«Giusto. Bé, se considero 1, quello ha argomento uguale a zero».

«E se moltiplichi zero per due rimane zero. Quindi la radice 1 al quadrato fa effettivamente 1».

«Se prendo -1, invece, quello ha argomento uguale a 180 gradi».

«Esatto. Se moltiplichi per due l'argomento, cosa ottieni?».

«Ottengo 360 gradi, che è come dire 0 gradi. Quindi anche -1 al quadrato fa 1. Ok, ci sono».

«Se osservi la figura, il punto rosso rappresenta il numero -1. Se lo elevi al quadrato, raddoppi il suo argomento: fai cioè fare un altro mezzo giro al punto, portandolo sul punto blu, che è 1».

«Ho capito. Ancora non riesco a capire, però, perché ci debbano essere n radici n-esime. Se prendo n = 3, dovrei avere tre radici cubiche, ma io ne vedo solo una, quella ovvia, cioè 1. Dove sono le altre due?».

«Te le faccio vedere».

«Uh, fammi capire».

«Nella figura vedi tre punti. Quello blu è il solito 1, non abbiamo bisogno di verificare che 1 alla terza fa 1».

«Ok».

«Quelle rosse sono le altre due radici dell'unità. Cioè sono altri due numeri che, elevati alla terza, danno 1. I segmenti tratteggiati servono solo per capire che le tre radici si trovano sui vertici di un triangolo equilatero, non servono per il calcolo».

«Allora, l'argomento di A dovrebbe essere 120 gradi, giusto?».

«Giusto. Se elevi A alla terza, come dovresti modificare il suo argomento?».

«Dovrei moltiplicarlo per tre, e 120 moltiplicato 3 fa 360, quindi vado a finire sul punto blu. Perfetto, anche A elevato alla terza fa 1. E B, invece?».

«Qual è l'argomento di B?».

«Uhm, 240 gradi?».

«Sì, che moltiplicato per 3…».

«…fa 720 gradi! Ho capito, faccio due giri e torno su 1. Bello!».

«Con un po' di calcoli che ti risparmio, si possono calcolare sia la parte reale che quella immaginaria di A e B».

«Dimmi come risultano».

«Ecco qua:».

«Bruttine».

«Sì, ma se provi ad elevare alla terza, risulta proprio 1 in entrambi i casi».

«E allora per le radici quarte avrò un quadrato?».

«Certo. Quali sono i numeri complessi che elevati alla quarta danno 1?».

«Allora, vediamo 1 e -1 di sicuro».

«Poi?».

«Forse i? Fammi pensare: i alla seconda fa -1, quindi alla quarta fa (-1)², cioè 1. Ho capito, le altre due radici sono i e -i».

«Ottimo. Eccole rappresentate sul piano complesso».

«Ah, ma certo, gli angoli sono di 90, 180 e 270 gradi. Se moltiplico per 4, arrivo sempre su 1».

«Sì, facendo un giro solo nel caso di i, due giri nel caso di -1 e tre giri nel caso di -i».

«E quindi tutte le radici dell'unità si possono trovare disegnando un poligono regolare?».

«Esatto. E qui ritrovi anche il risultato che avevi anticipato tu: se il poligono ha un numero pari di lati, un vertice cade su -1, altrimenti no. Questo significa che le radici n-esime dell'unità sono tutte complesse tranne una, se n è dispari, mentre sono tutte complesse tranne due, se n è pari».

«E quelle due sono 1 e -1. Perfetto, ho capito. Ma perché abbiamo parlato di questo argomento?».

«Per introdurre un ultimo argomento che stava a cuore ai greci: la costruzione di poligoni regolari mediante l'uso della riga e del compasso».

I greci non erano normali — 14: in matematica non si butta via niente

«E siamo arrivati al terzo periodo, quello che conclude la storia del pi greco».

«Siamo oltre l'analisi?».

«Bé, non oltre, ma ora l'analisi viene usata in maniera più approfondita. Partiamo da Hermite, che nel 1873 dimostrò che e è un numero trascendente».

«Eh? Cosa sarebbe?».

«Un numero è trascendente se non è soluzione di una equazione polinomiale a coefficienti interi».

«Di qualunque grado?».

«Già. La radice cubica di 2, per esempio, non è trascendente, perché è soluzione di x³ = 2».

«Ok. E se un numero non è trascendente, cosa è?».

«Un numero che non è trascendente si dice algebrico. I numeri reali vengono divisi in queste due grandi categorie; naturalmente i numeri razionali sono tutti algebrici, possiamo sempre scrivere un'equazione a coefficienti interi che abbia come soluzione una frazione del tipo n/d».

«Sì, è vero. Per esempio, dx = n».

«Infatti. Perciò la distinzione tra algebrico e trascendente diventa interessante quando parliamo di numeri irrazionali».

«Va bene, Il fatto che e sia trascendente cosa ha a che fare con π?».

«Eh, ora ci arriviamo. Nel 1882 Lindemann generalizzò il risultato di Hermite, dimostrando che in una equazione del tipo a₀ + a₁e^p₁ + a₂e^p₂ + … = 0 non solo i coefficienti e gli esponenti non possono essere interi, ma non possono essere nemmeno tutti algebrici».

«Quindi almeno uno deve essere trascendente?».

«Sì. E se applichiamo questo risultato all'equazione 1 + e^iπ = 0, dato che 1 è un numero algebrico, allora possiamo concludere che iπ deve essere trascendente».

«Ci sono. Immagino che ora dovremmo togliere quella i, si può?».

«Sì, si può, perché i numeri algebrici formano un campo. Questo significa che il prodotto di due numeri algebrici è algebrico. Ora ti domando: i è algebrico o trascendente?».

«Uhm, i, in effetti, è soluzione di una equazione facile».

«Quale?».

«x² = -1».

«Giusto, è una equazione a coefficienti interi».

«Quindi i è algebrico».

«E dato che iπ è trascendente, mentre il prodotto di due numeri algebrici è algebrico…».

«Allora π è trascendente!».

«Ottimo. Quindi π non è radice di nessuna equazione polinomiale, e dunque non può essere espresso mediante somme, sottrazioni, moltiplicazioni o divisioni di numeri razionali, né può essere il risultato di un quadrato o di una radice quadrata».

«E quindi non è costruibile con riga e compasso».

«Esatto. E allora non si può costruire un quadrato equivalente a un cerchio, utilizzando solo riga e compasso».

«Poveri greci».

I greci non erano normali — 13: arriva l'analisi

«Il secondo periodo della nostra storia vede personaggi come Newton, Fermat, Wallis, Eulero alle prese con lo studio di pi greco».

«Oh, gente famosa».

«I nuovi metodi dell'analisi hanno permesso a questi matematici di esprimere il valore di π come risultato di somme infinite, prodotti infiniti, frazioni continue».

«Tutta roba che i greci si sognavano».

«Già. Nel 1849 Jakob de Gelder, un matematico che esiste solo nella wikipedia olandese…».

«… che dice anche che nel 1849 il matematico era già morto…».

«Eh, le fonti qua non sono molto concordi… comunque, nel diciannovesimo secolo questo matematico, utilizzando le frazioni continue, arrivò a questa approssimazione:».

«Bleah».

«No, non è brutta. Devi sapere che la frazione 355/113 è molto importante: è la migliore frazione che approssima pi greco avente numeratore e denominatore di tre cifre».

«Non si può fare di meglio?».

«No, con tre cifre meglio di così non si fa. Anzi, se vuoi una frazione che migliora l'approssimazione fatta da 355/113, devi passare a 103993/33102».

«Gulp».

«Ma il nostro Jakob non si è fermato qua: ha anche spiegato come ottenere quella approssimazione utilizzando riga e compasso».

«Sarà complicatissimo».

«Un po'. Guarda questa figura:».

«Io la guardo, ma bisogna che me la spieghi».

«La circonferenza ha raggio 1, e il segmento OD è lungo 7/8».

«E già qui i numeri cominciano a essere brutti».

«Aspetta, allora. Congiungi A con D, e costruisci il segmento AF lungo 1/2».

«Mh, poi?».

«Poi traccia FG, perpendicolare ad AB, congiungi G con D e, finalmente, da F traccia la parallela a GD».

«E trovo il punto H».

«Ecco fatto. Se provi a fare i calcoli (che ti risparmio, però li ho fatti e ti assicuro che è vero), risulta che».

«E quindi mi basta aggiungere 3 per avere quella frazione che approssima pi greco tanto bene».

«Esatto».

«Però questo non dimostra che pi greco è irrazionale».

«No, ancora no. La dimostrazione del fatto che π è irrazionale è opera di Lambert. Lo dimostrò nel 1761. Anche se questo ancora non significa nulla, se vogliamo sapere se pi greco è costruibile con riga e compasso».

«Già. Con riga e compasso si possono costruire anche numeri irrazionali piuttosto brutti».

«Sì, è vero. Ma i matematici si stavano avvicinando alla soluzione. In particolare, un grosso passo avanti è stato fatto da un certo Eulero, con la sua apparentemente inutile formula più bella della matematica».

«Quale? e^iπ + 1 = 0?».

«Proprio quella».

I greci non erano normali — 12: approssimazioni con poligoni

«E siamo arrivati alla quadratura del cerchio».

«Che sarebbe?».

«Sarebbe la costruzione di un quadrato equivalente a un cerchio dato».

«Difficile?».

«Impossibile. Ma la scoperta dell'impossibilità della quadratura del cerchio, naturalmente usando solo riga e compasso, è stata una vicenda lunga e sofferta».

«Addirittura».

«Sì, ci è voluto molto tempo. Possiamo dividere la storia in tre grandi capitoli, che sono poi la storia di pi greco».

«Ah. Sì, in effetti immagino che pi greco c'entri, dato che parliamo di cerchi…».

«Eh, bé, sì. Prendi un cerchio di raggio 1, tanto per semplificare i conti. La sua area sarà π».

«E quindi io vorrei costruire un quadrato di lato √π».

«Esatto. Il nostro scopo è capire se la radice di pi greco possa essere costruita utilizzando solo riga e compasso».

«Va bene. Avevi parlato di tre periodi?».

«Sì. Il primo finisce a metà del diciassettesimo secolo».

«E parte?».

«Parte con Archimede. Il quale aveva calcolato le aree di tanti poligoni inscritti e circoscritti in una circonferenza, allo scopo di ottenere almeno una approssimazione decente per π».

«E ci è riuscito?».

«È arrivato a ragionare su poligoni di 96 lati…».

«Quanti?».

«Eh, hai capito bene, 96.».

«Ci assomiglia abbastanza, a un cerchio, eh».

«Già. Archimede ha trovato questa approssimazione:».

«Uhm, fammi fare i calcoli: pi greco risulta compreso tra 3.1408 e 3.1429. Meglio di quanto facciano gli studenti delle elementari».

«E delle medie… Da Archimede passiamo a Ludolph van Ceulen, sedicesimo secolo».

«Ah, e in mezzo ai due nessuno ha fatto progressi?».

«No, ci sono stati altri matematici che hanno migliorato un po' il risultato di Archimede, o che lo hanno ricavato in maniera autonoma, comunque sempre approssimando il cerchio con poligoni. Ludolph van Ceulen arrivò a 17 cifre dopo la virgola, e poi migliorò ancora i calcoli fino ad arrivare a 35 cifre, uilizzando poligoni con 2³⁰ lati. Era così orgoglioso del suo risultato, che volle che fosse inciso sulla sua lapide».

«Un altro pazzo furioso».

«Comunque, anche se erano stati fatti dei passi avanti dal punto di vista pratico, non si poteva dire altrettanto per la teoria. Ancora non si conosceva la natura di pi greco, non sapevano nemmeno se fosse razionale o irrazionale. E qui termina il primo periodo della nostra storia».

«E dopo che è successo?».

«Dopo è arrivata l'analisi».

I greci non erano normali — 11: la quadratura dei poligoni

«I greci erano in grado di costruire un quadrato equivalente a un qualunque poligono dato».

«Indipendentemente dal numero dei lati del poligono?».

«Sì, con un procedimento molto bello e generale».

«Mh, interessante».

«Tutto è basato sul fatto che triangoli aventi la stessa base e la stessa altezza sono equivalenti».

«Cioè hanno la stessa area?».

«Sì, anche se il concetto di equivalenza è un po' più astratto. Quando parli di area, usi i numeri, quando parli di equivalenza no».

«E cosa uso?».

«Niente. Cioè, usi il concetto di avere la stessa estensione, occupare la stessa superficie. Un concetto che, senza numeri, non è ulteriormente definibile. Negli Elementi di Euclide è un concetto primitivo, cioè non ulteriormente definibile. Ma se vuoi parlare di area, va benissimo».

«Sì, ho parlato di area perché mi è venuto in mente che l'area di un triangolo dipende proprio solo dalla base e dall'altezza».

«Infatti, è così, la formula per il calcolo dell'area di un triangolo funziona proprio perché tutti i triangoli aventi stessa base e stessa altezza sono equivalenti, e quindi l'area è sempre quella».

«Va bene. Vediamo questo procedimento, allora».

«Ecco qua, prendiamo un poligono qualsiasi, composto da un certo numero di lati. In questa figura, ne prendiamo cinque».

«Ok, un pentagono irregolare. Adesso?».

«Adesso scegliamo due vertici non adiacenti, ma tali che se percorriamo il bordo della figura, ci sia un solo vertice tra i due».

«Per esempio A e C?».

«Esatto: tra A e C abbiamo solo il vertice B. Congiungiamo A con C e, a partire da B, tracciamo una parallela ad AC».

«Ok, fin qua ci sono. So che con riga e compasso si riesce a tracciare una parallela a una retta data».

«Infatti. Ora prolunghiamo il lato DC verso C, fino ad incontrare la retta che abbiamo tracciato prima. Chiamiamo F il punto di intersezione».

«Ok, adesso?».

«Adesso abbiamo finito: il poligono AFDE è equivalente al precedente».

«Perché?».

«Perché i due triangoli ABC e AFC hanno la stessa base e la stessa altezza, mentre la parte composta dal poligono ACDE non è stata toccata dalla nostra costruzione».

«Ah, ecco. Sì, è vero, ma perché dici che abbiamo finito?».

«Perché questo è il procedimento: siamo partiti dal poligono ABCDE, cinque lati, e siamo arrivati al poligono AFDE, quattro lati».

«Ah! Quindi possiamo partire da un poligono di n lati, e arrivare a un poligono di n-1 lati».

«Certo, poi possiamo proseguire così fino ad arrivare a un poligono di tre lati, cioè un triangolo. E lì ci fermiamo».

«Bene, ci sono. Cioè, no, non avevi detto che dovevamo costruire un quadrato?».

«Sì, è vero. Per ora abbiamo ricondotto tutti i poligoni ai triangoli, e questo è già un passo notevole. Ora ricordati che puoi ricondurre un triangolo a un parallelogramma».

«Mmmh?».

«Guarda questa figura:».

«Ah, vedo. Però è un parallelogramma grande il doppio del triangolo».

«Esatto, poi ci ricorderemo di dividerlo a metà, ma non sarà un problema. Ora facciamo un passo avanti: ogni parallelogramma è equivalente a un rettangolo avente la stessa base e la stessa altezza, giusto?».

«Giusto, è una proprietà dei parallelogrammi».

«E anche il rettangolo è un parallelogramma. Quindi il nostro triangolo sarà equivalente a un rettangolo avente per base metà della base del triangolo, e la stessa altezza».

«Oppure la stessa base e altezza metà».

«Esatto. Quindi, riassumendo, per ora siamo in grado di passare da qualunque poligono a un rettangolo».

«Giusto. Rimane il passaggio da rettangolo a quadrato».

«Che possiamo fare utilizzando il secondo teorema di Euclide, che avevamo anche già usato in precedenza per estrarre la radice quadrata».

«Vediamo, in un triangolo rettangolo il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo avente per dimensioni le due proiezioni dei cateti sull'ipotenusa».

«Esatto. Eccoti la figura:».

«Uh, fammi capire».

«Partiamo dal rettangolo blu».

«Ok».

«Riportiamo l'altezza BC lungo il lato DC».

«Ok, lo facciamo col compasso».

«Esatto. Poi costruiamo la semicirconferenza di diametro DF».

«Sempre col compasso».

«Naturalmente. Ora troviamo il punto di intersezione della retta BC con la semicirconferenza, e abbiamo il triangolo rettangolo al quale applicare il teorema di Euclide».

«Il triangolo DFG. Se applico il teorema, risulta che CG² = DC·CF».

«Proprio così. Quindi il quadrato rosso è equivalente al rettangolo blu».

«Ah, ottimo. Quindi tutti i poligoni sono riconducibili a quadrati: molto bello».

«E così i greci erano a posto. Il passo successivo è stato quello di fare lo stesso giochino con la più semplice figura con i lati curvi, cioè la circonferenza».

«E ci sono riusciti?».

«No».

I greci non erano normali — 10: la trisezione dell'angolo

«Amici ateniesi!».

«Dicci, Sommo Matematico!».

«Siamo o non siamo i maestri della geometria?».

«Sììì!».

«Siamo noi in grado di realizzare costruzioni mirabolanti con riga e compasso?».

«Sììì!».

«Siamo noi i maestri della dimostrazione? Gli alfieri della logica? Abili scopritori dei segreti matematici?».

«Sììì, lo siamo!».

«Siamo noi in grado di prendere un angolo, e di dividerlo a metà?».

«Sììì!».

«E allora, cosa ci vuole a dividerlo in tre parti? Coraggio!».

«…».

«Perché non rispondete?».

«Eehhm».

«Cosa?».

«Non siam capaci».

«Vergogna! Venite, ragioniamo ancora un po' su queste dimostrazioni, portate nuove righe, portate altri compassi! Appuntite quelle matite! Coraggio, costruiamo!».





«Ci sono riusciti?».

«Eh, no, ».

«Non c'erano mica tanto con la testa, eh».

«Eh, magari erano ancora sotto gli effetti dell'epidemia che li aveva colpiti ai tempi della duplicazione del cubo».

«Ma smettila… Quindi anche questo è uno dei problemi irrisolvibili con riga e compasso, eh?».

«Già. Tagliare a metà un angolo è facile, in tre impossibile, anche se la dimostrazione è un po' più complicata rispetto a quella della duplicazione del cubo».

«Vediamo, vah».

«Va bene. Partiamo da questa formula di trigonometria:».

cos(3α) = 4cos³α - 3cosα.

«Mi fido».

«Ora consideriamo un angolo di 60 gradi, e lo sostituiamo al posto di 3α».

«Ok, quindi α sarebbe 20 gradi».

«Esatto».

«Ecco, dovrebbe essere così:».

cos(60°) = 4cos³(20°) - 3cos(20°).

«Bene, ricordati che il coseno di 60 gradi è noto, vale 1/2».

«Ah, già».

«Ora applica questa sostituzione: x = 2cos20°».

«Uh, ok. Diventa così: 1/2 = x³/2- 3x/2».

«E, se moltiplichiamo tutto per 2 e portiamo da una parte, otteniamo questa equazione:».

x³ - 3x - 1 = 0.

«Dobbiamo risolverla?».

«Sì, e dobbiamo capire se il risultato è un numero costruibile con riga e compasso».

«Ah, ma sappiamo risolvere un'equazione di terzo grado?».

«Sì, le formule sono note, ma non sempre sono utili».

«Perché?».

«Perché a volte usano numeri immaginari anche quando le soluzioni sono reali, e allora il risultato potrebbe essere poco chiaro ed evidente».

«Eh?».

«Guarda, se applichiamo la formula risolutiva (possiamo farlo fare a wolfram alpha, dato che siamo pigri), otteniamo queste bellezze:».

«Argh!».

«Ma, se facciamo i conti, otteniamo questi tre numerini:».

x₁ = -1.53209…
x₂ = -0.347296…
x₃ = 1.87939…

«Ah, ora capisco cosa intendi con risultato poco chiaro ed evidente. Così è meglio».

«Così è meglio, sì, ma ancora non sappiamo rispondere alla domanda iniziale: possiamo trisecare l'angolo?».

«Allora, un momento, fammi fare il punto: abbiamo scritto un'equazione valida per tutti gli angoli α».

«Giusto».

«Poi abbiamo sostituito α con 20 gradi».

«Sì».

«Abbiamo quindi una equazione valida in particolare per l'angolo di 20 gradi».

«Giusto anche questo».

«Poi abbiamo fatto una sostituzione, ed è sparito l'angolo α, mentre è comparso x».

«Sì. Tieni presente che x è legato all'angolo α, in realtà x è il doppio del coseno di 20 gradi. Tieni anche presente che se sappiamo costruire un angolo, allora sappiamo anche costruire il suo coseno, e viceversa. Sono costruzioni facilissime da fare con riga e compasso».

«Va bene. Quindi, dobbiamo capire se x è costruibile?».

«Esatto. Noi abbiamo elencato tre soluzioni dell'equazione di terzo grado, in realtà quella che ci interessa è quella positiva, perché il coseno di 20 gradi è un numero positivo».

«Va bene. Come facciamo allora a sapere se è costruibile?».

«Ecco, qua viene il difficile. Per prima cosa, si usa questo teorema: se una equazione di terzo grado ha una radice razionale, allora le sue radici sono costruibili. Altrimenti nessuna delle radici è costruibile».

«Ah. E questa è difficile da dimostrare?».

«Non è difficile, ma è noiosa. Non ti spiego tutta la dimostrazione, ma cerco di farti capire come funziona. La formula risolutiva generale per le equazioni di terzo grado contiene delle radici cubiche…».

«Che a noi non piacciono».

«Se non si semplificano, no, infatti. Allora, se una delle soluzioni è razionale, allora l'equazione di terzo grado si abbassa di grado facilmente e si ottiene un'equazione di secondo grado».

«Che noi sappiamo costruire».

«Esatto».

«Se invece l'equazione di terzo grado non ha una soluzione razionale, allora quelle radici cubiche rimangono, e non si semplificano».

«Va bene. Quindi a noi rimane da capire se la nostra equazione ammette una soluzione razionale?».

«Esatto. Supponiamo che esista questa benedetta soluzione, chiamiamola x = a/b, con a e b numeri interi, primi tra loro, e naturalmente b diverso da zero».

«Ok. Suppongo che tu stia facendo una dimostrazione per assurdo, vero?».

«Esatto. Prova a sostituire quindi x = a/b nell'equazione».

«Pronti: (a³/b³) - (3a/b) - 1 = 0».

«Bene. Eliminando i denominatori, abbiamo a³ - 3ab² = b³, cioè b³ = a(a² - 3b²)».

«E questo cosa ci dice?».

«Ci dice che a divide b³. Dato però che a e b sono primi tra loro, allora a deve essere uguale a +1 oppure a -1».

«Capisco».

«Ma possiamo anche scrivere l'uguaglianza precedente in modo diverso: a³ = b²(b + 3ab)».

«Quindi b² divide a³, giusto?».

«Certo, e questo significa che anche b è uguale a +1 oppure a -1. Ma allora se la nostra equazione ammette una soluzione razionale, questa deve essere +1 oppure -1».

«E ci basta sostituire per capire che non è vero».

«Esatto. Quindi niente soluzioni razionali, niente costruibilità con riga e compasso per il coseno di 20 gradi. Quindi abbiamo trovato almeno un angolo che non è divisibile in tre parti uguali».

«Nonostante gli sforzi dei poveri greci».

I greci non erano normali — 9: la duplicazione del cubo

Gli ateniesi si rivolsero all'oracolo di Delo allo scopo di far cessare l'epidemia che aveva colpito la città. L'oracolo rispose che essi avrebbero dovuto duplicare l'altare di Apollo, che aveva forma cubica. Gli ateniesi costruirono così un nuovo altare, avente il lato lungo il doppio di quello precedente, ma l'epidemia non si placò.

Gli ateniesi si rivolsero allora nuovamente all'oracolo, il quale disse: «Stolti! Non sapete nemmeno fare le moltiplicazioni? L'altare che avete costruito è grande otto volte il precedente, io vi avevo detto di costruirne uno grande il doppio!».

E gli ateniesi, avviliti, risposero: «Ma come si fa? Noi non siamo capaci di farlo».

E l'oracolo concluse: «Polli! Se vi ostinate a usare riga e compasso, non ce la fate di certo. Vedete un po' voi, o usate qualche altro strumento, oppure vi tenete l'epidemia».




«Bé?».

«Cosa?».

«E come è andata a finire?».

«La storia non lo racconta, probabilmente perché gli ateniesi sono morti tutti in seguito all'epidemia».

«Ma dai!».

«Comunque sia, questo è uno dei problemi classici che non si possono risolvere con riga e compasso».

«Si tratta di costruire un cubo di lato uguale al primo, moltiplicato per radice cubica di 2, no?».

«Esatto, ma abbiamo detto che la radice cubica di due è un numero che non si può costruire con riga e compasso. Non si può creare una radice cubica utilizzando solo radici quadrate».

«E quindi gli ateniesi non ci sono riusciti».

«Già. Bé, a loro mancava tutta la teoria algebrica, quindi non sapevano che quello fosse un problema impossibile da risolvere. Ci hanno provato in vari modi, ma quelli che funzionavano non utilizzavano solo riga e compasso».

«Poveretti».

«Già, tutti morti per non aver voluto cedere alla tentazione di usare altri strumenti, oltre a quelli leciti».

«Allora! La smettiamo?».

I greci non erano normali — 8: numeri costruibili con riga e compasso

«Abbiamo visto come, partendo dal campo dei numeri razionali, possiamo creare delle estensioni aggiungendo numeri irrazionali».

«Giusto».

«Abbiamo però anche detto che, con riga e compasso, possiamo costruire radici quadrate».

«Vero anche questo».

«Il procedimento di costruzione, poi, potrebbe prevedere più passi. Cioè, prima costruisco una radice, poi sommo un razionale, poi faccio un'altra radice, e così via».

«Eh?».

«Allora, andiamo per gradi. Avevamo chiamato F₀ il campo dei razionali, vero?».

«Sì».

«Prendiamo un elemento di F₀, uno qualunque».

«Prendiamo 4».

«Bene. Ora prendiamo un altro elemento di F₀ tale che la sua radice quadrata non sia razionale».

«Prendiamo 7, la radice di 7 non è razionale».

«Ottimo. Sommiamo questi due elementi».

«4+√7».

«E questo è un elemento di F₁».

«Ok. Adesso?».

«Adesso ricominciamo: prendiamo un elemento di F₁ la cui radice quadrata non appartenga a F₁».

«Uh, un momento. Bé, potrebbe andare bene anche il numero che abbiamo trovato prima, no? La radice di 4+√7 è una schifezza tale che sicuramente non appartiene a F₁».

«Siamo sicuri?».

«Bé, no, non lo so, ho sparato a caso».

«Ti è andata male, guarda:».

«Ma no, non è possibile!».

«Eppure è così: se provi ad elevare al quadrato a destra e a sinistra, ottieni lo stesso risultato».

«Ma questa magia funziona sempre?».

«Eh, no, funziona solo in alcuni casi. Un radicale doppio del tipo √(a+√b) si semplifica solo quando a²-b è un quadrato perfetto, quindi puoi cambiare esempio».

«Uff. Allora, invece di prendere 4+√7 prendo 3+√7, va bene?».

«Sì, quello va bene. Ora, se estendi il campo F₁ utilizzando la radice del tuo numero, ottieni il campo F₂ i cui elementi sono fatti così:».

«Se ho ben capito, questa volta A e B non sono numeri razionali, vero?».

«No, possono essere elementi di F₁, quindi a loro volta sono del tipo C+D√7».

«Ah».

«E poi osserva questo particolare: tu hai preso 7 come numero per passare da F₀ a F₁, e poi hai utilizzato ancora la radice di 7 (assieme a 3) per passare da F₁ a F₂, ma non è obbligatorio».

«In che senso?».

«Nel senso che puoi cambiare radici ogni volta che estendi, non devi fissarti solo su un valore».

«Fammi capire con qualche esempio».

«Allora, i numeri in F₀ sono i razionali, credo che qua non ci sia bisogno di fare esempi».

«No, andiamo avanti».

«Nella generazione successiva, cambiando di volta in volta la radice che usi per estendere F₀, puoi creare numeri come 1+√2 oppure 7-3√5, e così via».

«Va bene. Al passo successivo?».

«Ecco un paio di esempi di numeri contenuti in diversi F₂:».

«Ah, ecco».

«Riesci a dirmi in quale F_i è contenuto questo numero?».

«Oh, questo è complicato, vediamo. La radice di 5 si trova in F₁».

«Sì».

«E anche 7+√5».

«Esatto».

«La sua radice si trova invece in F₂».

«E anche 3 più quella radice, no?».

«Certo, giusto. Invece la radice di tutta quella espressione si trova in F₃. E la radice di quella radice allora si trova in F₄».

«E cosa mi dici della √2 che si trova all'inizio della formula?».

«Ah, niente, quella è in F₁, non dà fastidio, è contenuta in uno dei campi più vecchi. Quindi quel numerone lì è contenuto in F₄, giusto?».

«Giusto. E quindi è un numero costruibile con riga e compasso».

«Ah».

«Ora guarda questo numero: appartiene a qualche F_i?».

«Uhm, una radice cubica?».

«Sì, semplice semplice».

«Eh. Ma posso costruire radici cubiche, con quella faccenda delle estensioni di campi?».

«Tu cosa dici?».

«Posso fare radici quadrate, e radici di radici quadrate».

«Cioè radici di indice 4».

«Ma di indice 3 no».

«Esatto».

«E quindi?».

«E quindi quel numero non si può costruire con riga e compasso».

I greci non erano normali — 7: radici

Già i Pitagorici avevano scoperto che la diagonale di un quadrato è un numero incommensurabile con il lato del quadrato stesso. In termini moderni, questo significa che radice di 2 non è un numero razionale. Però si può costruire con riga e compasso: in effetti, abbiamo visto che ogni radice quadrata può essere costruita con riga e compasso.

«Vorrà dire che con riga e compasso si possono costruire tutti i numeri reali, e non solo i razionali, no?».

«Eh, no, non è così. È per questo motivo che i greci non sono riusciti a risolvere alcuni problemi, come ti avevo detto».

«Ah. Ma allora quali sono i numeri reali che non si riescono a costruire?».

«Eh, per rispondere a questa domanda dobbiamo tornare a parlare di algebra. Abbiamo detto che con le quattro operazioni possiamo costruire il campo dei numeri razionali».

«Vero».

«Chiamiamolo F₀».

«Mmmmh, come mi piace poco quell'indice…».

«F sta per field, mentre 0 sta a significare che poi ne faremo altri».

«Lo immaginavo».

«Allora, prendiamo un numero che non appartiene a F₀, per esempio la famosa radice di 2, e aggiungiamola all'insieme».

«Possiamo?».

«Certo che possiamo, i matematici possono fare tutto. Bisogna vedere se quello che fanno ha senso, ma questo è un altro discorso».

«Volevo dire: il nuovo insieme che otteniamo ha le proprietà di quello vecchio? È un campo?».

«Tu cosa dici?».

«Boh, non so, posso provare a guardarci. Ah, ma no, certo che no, mi basta fare una somma semplice: 1+√2 non sta in quell'insieme».

«Che, quindi, non è più un campo, perfetto. Ora, quanta roba dobbiamo aggiungere a F₀, oltre a √2, perché il nuovo insieme che otteniamo sia di nuovo un campo?».

«Uh, domanda difficile, vediamo. Se devo poter fare tutte le somme, l'insieme deve contenere numeri del tipo a+√2».

«Giusto. Ma se vuoi fare √2+√2?».

«Ah, quello fa 2√2. Ok, ci sono, l'insieme deve contenere numeri del tipo a+b√2».

«Bene, e così hai messo a posto le somme».

«Ok. Se voglio fare anche delle sottrazioni, bé, mi pare che non ci siano problemi, non devo aggiungere nient'altro».

«Esatto: la differenza tra a+b√2 e c+d√2 è ancora un numero del tipo A+B√2, quindi siamo a posto. Per quanto riguarda la moltiplicazione, invece?».

«Ah, ormai ho capito il trucco: provo a moltiplicare due numeri del tipo A+B√2 e guardo se il risultato è ancora di quel tipo lì oppure no».

«Prova».

«Subito. Allora, ecco qua: (a+b√2) + (c+d√2) dà come risultato (a+c) + (b+d)√2, che è ancora un numero del tipo A+B√2».

«Bene. Vediamo la divisione, adesso?».

«Subito. Ecco: (a+b√2) diviso (c+d√2) fa… uhm, non lo so mica quanto fa».

«Perché?».

«Eh, perché non la so fare la divisione con una radice».

«Sì, bé, in un certo senso nessuno la sa fare».

«Eh?».

«Sì, per dare un senso a una divisione del genere, i Veri Matematici usano un trucchetto che si chiama razionalizzazione del denominatore».

«Uh, mi pare di ricordare qualcosa dai miei studi di algebra».

«Bene. Ti ricordi come si fa?».

«Non tanto, mi pare che si dovesse moltiplicare la frazione, sia al numeratore che al denominatore, per una certa espressione, in modo da eliminare la radice di due al denominatore? Era una cosa del genere?».

«Esatto. Ti faccio vedere i passaggi:».

«Bello! Quindi anche con la divisione siamo a posto».

«Già, la divisione di due numeri del tipo A+B√2 produce un risultato dello stesso tipo».

«E quindi abbiamo ottenuto il nostro nuovo campo».

«Che, indovina un po', chiameremo F₁».

«Mh».

«Ci sarebbe da aggiungere una considerazione: quando si fa la divisione, si ottiene un denominatore».

«Sì, è c²-2d²».

«Ecco, bisogna che quel denominatore non diventi mai zero».

«Ah. Potrebbe diventarlo?».

«No, dato che stiamo lavorando con numeri razionali: se quel denominatore fosse uguale a zero, la radice di 2 dovrebbe essere un numero razionale».

«Cosa che non è vera».

«Infatti, e quindi siamo a posto. Ti faccio notare anche che il nuovo campo F₁ poteva essere costruito a partire da un qualunque numero irrazionale, radice di 2 non ha niente di speciale».

«Sì, giusto, se al posto di √2 usiamo √3 non cambia nulla, si possono ripetere gli stessi calcoli».

«Esatto. E se invece usiamo √4, potremmo avere dei valori di c e d che annullano il denominatore. Quindi, riassumendo ecco quello che abbiamo fatto: abbiamo preso il campo dei numeri razionali, abbiamo preso un elemento k tale che √k non è razionale, e abbiamo ampliato il campo costruendo tutti i numeri del tipo A+B√k, con A e B razionali».

«E questo è F₁».

«E poi ci saranno F₂, F₃, e così via».

«Grrr».

I greci non erano normali — 6: campi

Punto della situazione: i greci sapevano sommare, sottrarre, moltiplicare, dividere, elevare al quadrato ed estrarre la radice quadrata.

«Utilizzando riga e compasso».

«Esattamente. Ora trasferiamo il tutto nel linguaggio algebrico. Se, in geometria, fissiamo una unità di misura, in algebra diciamo semplicemente che prendiamo il numero 1».

«E da lì cominciamo a fare operazioni?».

«Sì. Se noi cominciamo a creare numeri sommando, e abbiamo a disposizione come mattone iniziale il numero 1, cosa possiamo costruire?».

«Tutti i numeri naturali».

«Bene. Anche se cominciamo a fare sottrazioni?».

«No».

«Perché?».

«Bé, per esempio 1-3 non è un numero naturale».

«Benissimo. Quindi l'insieme dei numeri naturali non è chiuso rispetto alla sottrazione. Se noi allora cominciamo a sommare e sottrarre tutto ciò che otteniamo, quale sarà l'insieme che conterrà tutti i nostri risultati?».

«Quello dei numeri interi».

«Perfetto. Se moltiplichiamo?».

«Se moltiplichiamo utilizzando solo il numero 1, rimaniamo nei naturali. Se però usiamo anche i numeri negativi, siamo all'interno dell'insieme dei numeri interi».

«E dividendo?».

«Ah, dividendo usciamo da quell'insieme. Potremmo creare anche le frazioni».

«Sì, è vero. Qual è, quindi, l'insieme che contiene tutti i possibili risultati che si possono ottenere applicando al numero 1 le quattro operazioni?».

«L'insieme dei numeri razionali».

«Bene. I Veri Matematici dicono che l'insieme dei razionali è un campo».

«Campo?».

«Campo. In parole povere, significa quello che abbiamo appena detto. Dato però che i Veri Matematici vanno matti per le definizioni più stringate possibili, posso anticiparti che la definizione rigorosa di campo è quasi incomprensibile, a prima vista».

«Capirai».

«La definizione è questa: un campo è una struttura algebrica K dotata di due operazioni binarie, chiamate somma e moltiplicazione, tale che K, assieme alla somma, è un gruppo abeliano con elemento neutro 0, mentre K-{0}, assieme al prodotto, è un gruppo abeliano con elemento neutro 1, e infine la moltiplicazione è distributiva rispetto alla somma».

«Non ho capito quasi niente, se non che ci sono due operazioni, quando invece noi ne abbiamo quattro».

«Ti ho pur detto che la definizione è la più stringata possibile, no? All'interno della definizione di gruppo è prevista l'esistenza di un elemento inverso, che ci permette di risparmiare le parole sottrazione e divisione».

«Roba da matti. E un gruppo abeliano cosa sarebbe?».

«Un gruppo è una struttura algebrica più semplice, dotata di una operazione sola, la quale gode di alcune proprietà che sono il minimo sindacale, se si vuole costruire una struttura che funzioni in modo decente».

«Quali sono queste proprietà?».

«L'operazione deve godere della proprietà associativa, deve esistere l'elemento neutro, e deve esistere l'inverso. La parola abeliano significa che vale anche la proprietà commutativa».

«Mh, vabbé, mi sembrano proprietà ragionevoli».

«Ma sì, il prototipo di campo è proprio l'insieme dei numeri razionali. Un campo gode di tutte quelle belle proprietà a cui siamo abituati».

«Va bene, ho capito. Mi sfugge però il senso di quello che stiamo facendo: tutto questo discorso servirebbe per dire che…?».

«Che, utilizzando riga e compasso, riusciamo a costruire almeno tutti i razionali».

«Almeno? Ah, già, è vero: con riga e compasso si possono anche fare quadrati e radici quadrate. Cambia molto?».

«Per quanto riguarda i quadrati, non cambia nulla: un quadrato puoi sempre vederlo come prodotto di un numero per sé stesso».

«E per quanto riguarda le radici?».

«Bella domanda».

I greci non erano normali — 5: risoluzione di un'equazione di secondo grado con riga e compasso

«Un'equazione di secondo grado di solito si scrive così:».

ax² + bx + c = 0.

«Sì, questo l'ho studiato in seconda superiore».

«Una equazione di questo tipo, quindi, è determinata da tre parametri: i coefficienti a, b e c. Dato che però è uguagliata a zero, possiamo dividere tutto per a e semplificarla un po'».

«Sì, è vero, dopo rimangono solo due coefficienti. Però sono delle frazioni, mi piace di meno».

«Bé, questo non è un problema. Possiamo usare una delle tecniche preferite dai Veri Matematici».

«Quale?».

«Cambiare nome alle cose per farle sembrare più semplici».

«Ah».

«In questo caso, la nostra equazione potrebbe essere scritta così:».

x² - Sx + P = 0.

«Perché proprio S e P?».

«Perché se passa per caso di qua qualcuno che si ricorda la relazione tra le radici e i coefficienti di un'equazione di secondo grado, si ritrova. Se risolvi l'equazione, ottieni che S è uguale alla somma delle soluzioni, mentre P è uguale al loro prodotto».

«Uh, è vero, è un'altra di quelle cose su cui il prof insisteva».

«Eh, infatti. Comunque, andiamo avanti. Ora consideriamo, sul piano cartesiano, i punti A(0,1) e B(S,P), poi costruiamo la circonferenza avente diametro AB».

«Va bene, questo con riga e compasso si fa senza problemi».

«Proviamo a calcolare la sua equazione?».

«Proviamo. Allora, il centro è il punto medio del segmento AB, quindi dovrebbe avere coordinate uguali a S/2 e (P+1)/2».

«Esatto, chiamiamolo C».

«Il raggio è uguale alla distanza AC».

«Sì, e risulta la radice quadrata di S²/4 + (P-1)²/4».

«Bleah».

«Sì, non è un gran che. Ora, l'equazione della circonferenza diventa questa:».

«Sempre peggio».

«Eh, lo so, ma c'è poco da fare. Comunque ormai abbiamo finito: se poni y = 0, in modo da trovare le intersezioni con l'asse delle x, ottieni proprio le soluzioni della equazione iniziale».

«Mh, mi sono perso. Alla fine a cosa sono serviti questi calcoli?».

«A spiegare questa figura: le soluzioni dell'equazione di secondo grado sono i punti di intersezione della circonferenza con l'asse delle x. Usando riga e compasso fai in un attimo».

I greci non erano normali — 4: passiamo alla geometria analitica

I greci, quindi, potevano fare costruzioni geometriche che richiedevano un numero finito di somme, sottrazioni, moltiplicazioni, divisioni, quadrati e radici quadrate. Ma non erano in grado di dire se un qualunque problema fosse risolubile o no con riga e compasso.

«Perché?».

«Eh, dato un certo problema, se erano in grado di risolverlo con riga e compasso, bene. Ma se non ci riuscivano?».

«Allora il problema non era risolubile con riga e compasso».

«Eh, non è mica detto. O davvero non era risolubile, oppure loro non avevano ancora trovato il modo di farlo».

«Ah. E quindi?».

«E quindi i greci ci hanno lasciato alcuni problemi che loro non erano stati capaci di risolvere».

«E noi ci siamo riusciti?».

«No, ma abbiamo fatto di più. Abbiamo dimostrato che è impossibile risolverli utilizzando solo riga e compasso».

«Saranno problemi complicatissimi».

«No, sono molto semplici. Spesso i problemi più difficili hanno enunciati molto semplici. Ad esempio, costruire un angolo uguale a un terzo di un dato angolo».

«È un enunciato molto semplice, in effetti».

«Oppure costruire un quadrato avente superficie uguale a quella di un cerchio dato. O ancora, costruire un cubo avente volume doppio di quello di un altro cubo».

«Facili anche questi. E quindi adesso siamo in grado di capire quali problemi sono risolubili con riga e compasso, e quali non lo sono?».

«Sì».

«E come si fa a capirlo?».

«Serve uno strumento che i greci non avevano: la geometria analitica».

«Ah. Trasformiamo tutto in equazioni, quindi?».

«Esatto. Riconsideriamo le operazioni di base che si possono fare con riga e compasso, e le traduciamo in formule. Poi ci ragioniamo su».

«Allora, vediamo. Con la riga si può tracciare una retta passante per due punti».

«Bene. Se noi utilizziamo il piano cartesiano, ad ogni punto possiamo associare le sue coordinate. Quindi, dati due punti A(x_A,y_A) e B(x_B,y_B), siamo capaci di scrivere l'equazione della retta che passa per questi punti?».

«Sì, direi di sì, l'ho imparato a scuola. Ci sono vari modi, se ben ricordo».

«Sì, la formula più generale, quella che non ha casi particolari e che non distingue tra rette verticali, orizzontali o oblique, è questa:».

x(y_B-y_A) - y(x_B-x_A) - x_Ay_B + y_Ax_B = 0.

«Bruttina».

«Eh, sì, ma non importa, non dobbiamo fare dei gran calcoli. Dobbiamo solo capire quello che si può e quello che non si può fare».

«Va bene, allora così abbiamo messo a posto la riga. Passiamo al compasso?».

«Sì, col compasso si può costruire una circonferenza dati il centro e il raggio. Come si fa in geometria analitica?».

«Ah, questa era una domanda classica a scuola. Allora, l'equazione della circonferenza dati centro e raggio è questa:».

(x-x_C)² + (y-y_C)² = R².

«Esatto, è proprio quella».

«Quindi siamo a posto».

«No, ancora no. Con riga e compasso si possono fare altre cose».

«Che cosa?».

«Trovare le intersezioni tra gli oggetti che abbiamo disegnato».

«Ah, è vero. Però è facile: per trovare l'intersezione tra due rette, occorre mettere a sistema le equazioni delle due rette».

«Sì, e si ottiene un sistema di primo grado, che sappiamo risolvere senza problemi».

«Sì, lo so fare. Se intersechiamo una retta e una circonferenza, abbiamo un sistema di secondo grado».

«E anche quello è semplice, sappiamo risolverlo, no?».

«Sì, conosco la formula risolutiva delle equazioni di secondo grado. Ma allora, se vogliamo trovare l'intersezione tra due circonferenze, dovremmo risolvere un sistema di quarto grado? Quella formula non la so».

«Sì, il sistema sarebbe di quarto grado. Ma si riduce sempre a un sistema di secondo grado».

«E come si fa?».

«Se tu svolgi le equazioni delle due circonferenze di cui vuoi calcolare l'intersezione, ti accorgi che hai sempre due termini uguali, che sono x² e y²».

«E che sono anche gli unici termini di secondo grado».

«Esatto. Se tu sottrai membro a membro le equazioni di secondo grado, quei termini lì spariscono, si cancellano».

«E rimango con un'equazione di primo grado».

«Proprio così. Allora prendi quella equazione, la metti a sistema con una delle due circonferenze, ed ecco fatto, hai un sistema di secondo grado che sai risolvere».

«Mh, interessante. Quindi, riassumendo…».

«Riassumendo: le costruzioni con riga e compasso si traducono in operazioni con equazioni di primo oppure di secondo grado».

«Vale anche il viceversa? Tutte le operazioni con equazioni di primo e secondo grado sono fattibili con riga e compasso?».

«Abbiamo praticamente già risposto: per risolvere una equazione di primo grado, è sufficiente sapere calcolare somme, sottrazioni, prodotti e divisioni. Per quelle di secondo grado servono anche quadrati e radici quadrate. Quindi, sì, la risposta è sì».

«Però costruire le soluzioni di un'equazione di secondo grado diventa complicato. Devo procedere passo passo, ricalcando la formula che non è proprio semplicissima».

«Giusto. In linea di principio è possibile costruirle, e tanto ci basta. Ma possiamo farlo anche in modo più immediato: la prossima volta lo vediamo».

I greci non erano normali — 3: operazioni geometriche

I greci, utilizzando riga e compasso, erano in grado di eseguire le quattro operazioni, il quadrato e la radice quadrata.

«Cosa intendi quando dici che si possono fare le operazioni con riga e compasso?».

«Per esempio, dati due segmenti di lunghezza a e b, costruire il segmento di lunghezza a+b».

«Ah, capisco. Questo è facile, si mettono i segmenti uno dietro l'altro e si ha il risultato».

«Infatti, e altrettanto facile è costruire a-b; con a maggiore di b, naturalmente».

«Sì, sono cose che si fanno alle elementari. Invece, per quanto riguarda il prodotto ab? Devo costruire il rettangolo?».

«Eh, no. Il rettangolo ha effettivamente area ab, ma noi vogliamo un segmento di lunghezza ab».

«Ah. Allora non saprei come fare».

«Guarda questa costruzione».

«Uhm, mi ricorda un teorema che ho studiato a scuola».

«Sì, si chiama teorema di Talete, e afferma che se BD e CE sono paralleli, allora AB:BC=AD:DE».

«Ora ricordo: i segmenti sulla prima trasversale sono proporzionali ai segmenti sulla seconda».

«Sì. Detto in altri termini, il prodotto AB per DE è uguale a BC per AD».

«E dato che AB è uguale a 1, abbiamo che x è uguale a ab, e abbiamo costruito il prodotto. Bello».

«Sì. Naturalmente quando facciamo calcoli coi segmenti, abbiamo bisogno di una unità di misura. Nella nostra costruzione l'unità di misura è il segmento AB».

«Bene, ho capito».

«Se sai costruire ab, sai anche costruire a²».

«Ah, certo, basta porre a=b».

«Giusto. Ora prova a pensare a come fare per costruire a/b».

«Uhm, non saprei. Qui abbiamo imparato a fare le moltiplicazioni, ma con le divisioni come si fa?».

«Ricordati che abbiamo usato una proporzione, che è una uguaglianza tra due rapporti. Quindi la divisione c'è, bisogna solo usarla bene».

«Forse ho capito: scambio di posto 1 e b?».

«Esatto. Se poni AB=b e AD=1, hai che xb=a, cioè x=a/b».

«Benissimo. Rimane la radice quadrata, allora».

«Sì. Per quella dobbiamo usare un teorema diverso, quello che di solito si chiama secondo teorema di Euclide».

«In un triangolo rettangolo, il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo avente per dimensioni le proiezioni dei cateti sull'ipotenusa. Giusto, vero? Il prof ce lo faceva ripetere sempre».

«Ve lo faceva studiare a memoria?».

«All'inizio pensavo di sì, poi però quando finalmente ero riuscito a imparare a memoria l'enunciato, lui mi ha detto "bravo, adesso dimmi cosa vuol dire", e io sono rimasto lì come un pesce lesso».

«Perché non avevi capito niente?».

«Eh, no. Lui voleva delle parole precise, io ho detto le parole precise. Poi mi sono reso conto che lui voleva che capissimo quello che stavamo dicendo».

«E magari, capendo quello che si sta studiando, si fa anche meno fatica a studiare, vero?».

«Ehm, già».

«Ottimo, mi piace il tuo prof. Allora, dato che sai cosa dice il secondo teorema di Euclide, eccoti un disegnino».

«Uhm, fammi capire. Vedo il triangolo rettangolo, ma vedo anche una semicirconferenza, come mai?».

«Ricordati che stiamo utilizzando riga e compasso. Il triangolo rettangolo c'è, ma non è necessario disegnarlo. Dato che ogni triangolo inscritto in una semicirconferenza è rettangolo, ci basta disegnare la semicirconferenza».

«Vero, questo me lo ricordo. Quindi, alla fine, per fare questa figura ci servono solo i segmenti AC e CB, giusto? Poi traccio la perpendicolare in C e trovo D».

«Esatto, questi due segmenti sono i nostri dati. L'unità, quella c'è sempre, e il segmento a di cui vogliamo calcolare la radice quadrata. Ora, se applichi il teorema di Euclide…».

«Ottengo che x² è uguale al prodotto di a per 1. Cioè il quadrato di x è uguale ad a, quindi x è uguale alla radice quadrata di a. Ottimo. Ma tutte queste costruzioni si possono fare con riga e compasso?».

«Sì, sia la costruzione della parallela che la costruzione della perpendicolare sono costruzioni standard. Le proposizioni 11 e 12 degli Elementi di Euclide riguardano la costruzione della perpendicolare, mentre la proposizione 31 spiega come costruire la parallela».

«Va bene. Quindi con riga e compasso possiamo costruire somme, prodotti, moltiplicazioni, divisioni, quadrati e radici quadrate. C'è altro?».

«Continui a fare belle domande».