«Oh, gente famosa».
«I nuovi metodi dell'analisi hanno permesso a questi matematici di esprimere il valore di π come risultato di somme infinite, prodotti infiniti, frazioni continue».
«Tutta roba che i greci si sognavano».
«Già. Nel 1849 Jakob de Gelder, un matematico che esiste solo nella wikipedia olandese…».
«… che dice anche che nel 1849 il matematico era già morto…».
«Eh, le fonti qua non sono molto concordi… comunque, nel diciannovesimo secolo questo matematico, utilizzando le frazioni continue, arrivò a questa approssimazione:».
«Bleah».
«No, non è brutta. Devi sapere che la frazione 355/113 è molto importante: è la migliore frazione che approssima pi greco avente numeratore e denominatore di tre cifre».
«Non si può fare di meglio?».
«No, con tre cifre meglio di così non si fa. Anzi, se vuoi una frazione che migliora l'approssimazione fatta da 355/113, devi passare a 103993/33102».
«Gulp».
«Ma il nostro Jakob non si è fermato qua: ha anche spiegato come ottenere quella approssimazione utilizzando riga e compasso».
«Sarà complicatissimo».
«Un po'. Guarda questa figura:».
«Io la guardo, ma bisogna che me la spieghi».
«La circonferenza ha raggio 1, e il segmento OD è lungo 7/8».
«E già qui i numeri cominciano a essere brutti».
«Aspetta, allora. Congiungi A con D, e costruisci il segmento AF lungo 1/2».
«Mh, poi?».
«Poi traccia FG, perpendicolare ad AB, congiungi G con D e, finalmente, da F traccia la parallela a GD».
«E trovo il punto H».
«Ecco fatto. Se provi a fare i calcoli (che ti risparmio, però li ho fatti e ti assicuro che è vero), risulta che».
«E quindi mi basta aggiungere 3 per avere quella frazione che approssima pi greco tanto bene».
«Esatto».
«Però questo non dimostra che pi greco è irrazionale».
«No, ancora no. La dimostrazione del fatto che π è irrazionale è opera di Lambert. Lo dimostrò nel 1761. Anche se questo ancora non significa nulla, se vogliamo sapere se pi greco è costruibile con riga e compasso».
«Già. Con riga e compasso si possono costruire anche numeri irrazionali piuttosto brutti».
«Sì, è vero. Ma i matematici si stavano avvicinando alla soluzione. In particolare, un grosso passo avanti è stato fatto da un certo Eulero, con la sua apparentemente inutile formula più bella della matematica».
«Quale? eiπ + 1 = 0?».
«Proprio quella».
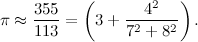
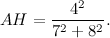
Nessun commento:
Posta un commento