«E siamo arrivati alla quadratura del cerchio».
«Che sarebbe?».
«Sarebbe la costruzione di un quadrato equivalente a un cerchio dato».
«Difficile?».
«Impossibile. Ma la scoperta dell'impossibilità della quadratura del cerchio, naturalmente usando solo riga e compasso, è stata una vicenda lunga e sofferta».
«Addirittura».
«Sì, ci è voluto molto tempo. Possiamo dividere la storia in tre grandi capitoli, che sono poi la storia di pi greco».
«Ah. Sì, in effetti immagino che pi greco c'entri, dato che parliamo di cerchi…».
«Eh, bé, sì. Prendi un cerchio di raggio 1, tanto per semplificare i conti. La sua area sarà π».
«E quindi io vorrei costruire un quadrato di lato √π».
«Esatto. Il nostro scopo è capire se la radice di pi greco possa essere costruita utilizzando solo riga e compasso».
«Va bene. Avevi parlato di tre periodi?».
«Sì. Il primo finisce a metà del diciassettesimo secolo».
«E parte?».
«Parte con Archimede. Il quale aveva calcolato le aree di tanti poligoni inscritti e circoscritti in una circonferenza, allo scopo di ottenere almeno una approssimazione decente per π».
«E ci è riuscito?».
«È arrivato a ragionare su poligoni di 96 lati…».
«Quanti?».
«Eh, hai capito bene, 96.».
«Ci assomiglia abbastanza, a un cerchio, eh».
«Già. Archimede ha trovato questa approssimazione:».
«Uhm, fammi fare i calcoli: pi greco risulta compreso tra 3.1408 e 3.1429. Meglio di quanto facciano gli studenti delle elementari».
«E delle medie… Da Archimede passiamo a Ludolph van Ceulen, sedicesimo secolo».
«Ah, e in mezzo ai due nessuno ha fatto progressi?».
«No, ci sono stati altri matematici che hanno migliorato un po' il risultato di Archimede, o che lo hanno ricavato in maniera autonoma, comunque sempre approssimando il cerchio con poligoni. Ludolph van Ceulen arrivò a 17 cifre dopo la virgola, e poi migliorò ancora i calcoli fino ad arrivare a 35 cifre, uilizzando poligoni con 230 lati. Era così orgoglioso del suo risultato, che volle che fosse inciso sulla sua lapide».
«Un altro pazzo furioso».
«Comunque, anche se erano stati fatti dei passi avanti dal punto di vista pratico, non si poteva dire altrettanto per la teoria. Ancora non si conosceva la natura di pi greco, non sapevano nemmeno se fosse razionale o irrazionale. E qui termina il primo periodo della nostra storia».
«E dopo che è successo?».
«Dopo è arrivata l'analisi».

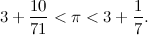
2 commenti:
hai dimenticato cinesi e indiani.
accidenti, gli indiani usavano le serie prima che fosse scoperta l'analisi...
Posta un commento