«Giusto».
«Abbiamo però anche detto che, con riga e compasso, possiamo costruire radici quadrate».
«Vero anche questo».
«Il procedimento di costruzione, poi, potrebbe prevedere più passi. Cioè, prima costruisco una radice, poi sommo un razionale, poi faccio un'altra radice, e così via».
«Eh?».
«Allora, andiamo per gradi. Avevamo chiamato F0 il campo dei razionali, vero?».
«Sì».
«Prendiamo un elemento di F0, uno qualunque».
«Prendiamo 4».
«Bene. Ora prendiamo un altro elemento di F0 tale che la sua radice quadrata non sia razionale».
«Prendiamo 7, la radice di 7 non è razionale».
«Ottimo. Sommiamo questi due elementi».
«4+√7».
«E questo è un elemento di F1».
«Ok. Adesso?».
«Adesso ricominciamo: prendiamo un elemento di F1 la cui radice quadrata non appartenga a F1».
«Uh, un momento. Bé, potrebbe andare bene anche il numero che abbiamo trovato prima, no? La radice di 4+√7 è una schifezza tale che sicuramente non appartiene a F1».
«Siamo sicuri?».
«Bé, no, non lo so, ho sparato a caso».
«Ti è andata male, guarda:».
«Ma no, non è possibile!».
«Eppure è così: se provi ad elevare al quadrato a destra e a sinistra, ottieni lo stesso risultato».
«Ma questa magia funziona sempre?».
«Eh, no, funziona solo in alcuni casi. Un radicale doppio del tipo √(a+√b) si semplifica solo quando a2-b è un quadrato perfetto, quindi puoi cambiare esempio».
«Uff. Allora, invece di prendere 4+√7 prendo 3+√7, va bene?».
«Sì, quello va bene. Ora, se estendi il campo F1 utilizzando la radice del tuo numero, ottieni il campo F2 i cui elementi sono fatti così:».
«Se ho ben capito, questa volta A e B non sono numeri razionali, vero?».
«No, possono essere elementi di F1, quindi a loro volta sono del tipo C+D√7».
«Ah».
«E poi osserva questo particolare: tu hai preso 7 come numero per passare da F0 a F1, e poi hai utilizzato ancora la radice di 7 (assieme a 3) per passare da F1 a F2, ma non è obbligatorio».
«In che senso?».
«Nel senso che puoi cambiare radici ogni volta che estendi, non devi fissarti solo su un valore».
«Fammi capire con qualche esempio».
«Allora, i numeri in F0 sono i razionali, credo che qua non ci sia bisogno di fare esempi».
«No, andiamo avanti».
«Nella generazione successiva, cambiando di volta in volta la radice che usi per estendere F0, puoi creare numeri come 1+√2 oppure 7-3√5, e così via».
«Va bene. Al passo successivo?».
«Ecco un paio di esempi di numeri contenuti in diversi F2:».
«Ah, ecco».
«Riesci a dirmi in quale Fi è contenuto questo numero?».
«Oh, questo è complicato, vediamo. La radice di 5 si trova in F1».
«Sì».
«E anche 7+√5».
«Esatto».
«La sua radice si trova invece in F2».
«E anche 3 più quella radice, no?».
«Certo, giusto. Invece la radice di tutta quella espressione si trova in F3. E la radice di quella radice allora si trova in F4».
«E cosa mi dici della √2 che si trova all'inizio della formula?».
«Ah, niente, quella è in F1, non dà fastidio, è contenuta in uno dei campi più vecchi. Quindi quel numerone lì è contenuto in F4, giusto?».
«Giusto. E quindi è un numero costruibile con riga e compasso».
«Ah».
«Ora guarda questo numero: appartiene a qualche Fi?».
«Uhm, una radice cubica?».
«Sì, semplice semplice».
«Eh. Ma posso costruire radici cubiche, con quella faccenda delle estensioni di campi?».
«Tu cosa dici?».
«Posso fare radici quadrate, e radici di radici quadrate».
«Cioè radici di indice 4».
«Ma di indice 3 no».
«Esatto».
«E quindi?».
«E quindi quel numero non si può costruire con riga e compasso».
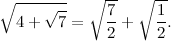
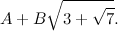
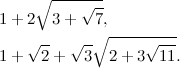
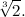
5 commenti:
Sempre più complicato ma intrigante! :-)
g
Basta, non si complica più...
Come Basta? Finiti?
ooooh! :)
g
finite le cose difficili...
aaaah! :-)
g
Posta un commento