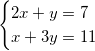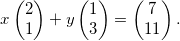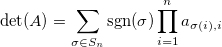E quindi, Cramer?

“Cramer! Chi era costui? — ruminava tra sé il Vero Matematico seduto sul suo seggiolone, in una stanza del piano superiore, con un libricciolo aperto davanti…”.

“Ma cosa stai dicendo?”.

“Avevi iniziato a parlare dei determinanti, pensavo che prima o poi mi avresti raccontato anche del misterioso metodo di Cramer per la risoluzione dei sistemi”.

“Hai ragione, rimedio subito! Cosa significa risolvere un sistema?”.

“Eh, significa trovare i valori delle incognite che rendono vere entrambe le equazioni, se non mi sbaglio”.

“Giusto, è così. Ma adesso vorrei mostrarti la cosa da un altro punto di vista”.

“Capirai, fai sempre così!”.

“Guarda che è questo il bello della matematica, vedere le cose da diversi punti di vista, riconoscere analogie, creare collegamenti, ed essere felici per questo”.

“…”.

“Comunque, ti propongo un nuovo punto di vista sui sistemi, e lo faccio con un esempio, così abbiamo dei numeri con cui giocare. Eccoti il testo di un esercizio:”.

“Ok, non mi sembra difficile, fammi fare un po' di conti… mi pare che risulti x = 2 e y = 3”.

“Bene, fin qua ci siamo. Adesso permettimi di scrivere il sistema in un modo leggermente diverso, ecco:”.

“Uh? Ma che roba è”.

“Possiamo vederla come una scrittura in forma vettoriale del sistema di prima: quei numeri scritti tra le parentesi sono le componenti dei vettori”.

“Quindi, per capire, all'inizio sto moltiplicando x per il vettore avente componenti 2 e 1?”.

“Esatto. Per dirla in un altro modo, stiamo considerando la prima riga del sistema come una descrizione di quello che succede nel mondo delle ascisse di certi vettori, e la seconda riga, invece, come una descrizione di quello che succede nel mondo delle ordinate”.

“Ma le ascisse sono le x, che compaiono sia nella prima che nella seconda riga. E anche le ordinate, eh”.

“Non fare confusione, le x e le y che vedi nel sistema non c'entrano con le ascisse e le ordinate di cui ti sto parlando. Tu hai un vettore, che ha componenti 2 e 1…”.

“Ascissa 2 e ordinata 1”.

“Esatto. Lo moltiplichi per x, cioè ne vari la lunghezza, e ottieni un altro vettore…”.

“Di ascissa 2x e ordinata x?”.

“Proprio così. Poi hai un secondo vettore, di componenti 1 e 3. Questo lo moltiplichi per y”.

“E ottengo un vettore di componenti y e 3y”.

“Sì. Adesso li sommi: ti ricordi come si fa la somma tra due vettori?”.

“Si fa componente per componente. Il risultato dovrebbe essere il vettore di ascissa 2x + y e di ordinata x + 3y”.

“E queste sono le due righe del sistema. Cioè, le due parti a sinistra dell'uguale”.

“Ah, ho capito. E il sistema quindi ci domanda quanto devono valere x e y perché il vettore risultante sia quello di componenti 7 e 11?”.

“Ottimo, hai detto bene: traducendo in linguaggio geometrico, il sistema ci domanda di quanto devo allungare i due vettori (2,1) e (1,3) perché il risultato sia il vettore (7,11)”.

“E quindi potrei fare anche un disegnino, con questi vettori? Giusto per vedere meglio le cose”.

“Naturalmente. Puoi giocare con la figura qua sotto: in rosso sono indicati i vettori u e v, che sono i vettori (2,1) e (1,3). Puoi trascinare il punto viola dove vuoi, e osservare come devono essere modificati i due vettori dati perché la loro somma dia il vettore che termina sul punto viola”.



“Mh, carino, ma il punto rosso cosa sarebbe?”.

“È il punto di coordinate (7,11), cioè il punto dove tu vorresti fare andare la punta del vettore”.

“Beh, posso trascinarcela sopra, no?”.

“Certo. Se lo fai, puoi vedere come devono essere modificati i vettori u e v in modo tale che la loro somma finisca proprio su (7,11)”.

“Provo… a occhio mi sembra che il vettore u raddoppi…”.

“Eh eh”.

“Cosa c'è da ridere?”.

“Magari ti sembra anche che il vettore v triplichi?”.

“Mh, non riesco a vederlo bene a occhio, ma potrebbe essere. Continuo a non capire perché ridacchi, però”.

“Perché hai già risolto il sistema prima! Non avevi trovato x = 2 e y = 3?”.

“Sì, ma cosa c'entra… Ah! Ma certo! Il fatto che x sia uguale a 2 significa che devo moltiplicare il vettore u per 2, e il fatto che y sia uguale a 3 significa che devo moltiplicare v per 3, e il risultato è proprio (7,11). Ma guarda un po', non avevo mai visto un sistema risolto in questo modo”.

“Bello, vero? In pratica abbiamo interpretato il sistema come un'equazione vettoriale. Se diamo un nome anche al vettore risultante, cioè (7,11)…”.

“A questo punto chiamiamolo w”.

“Bene, se poniamo allora w = (7,11), il sistema che abbiamo scritto prima può essere riscritto così:”.

xu + yv = w.

“Molto semplice”.

“E però non possiamo mica sempre trovare x e y a occhio, no?”.

“Eh, no. Ma questa visualizzazione ci aiuterà molto nella ricerca di un metodo risolutivo”.

“Il famoso metodo di Cramer?”.

“Proprio lui”.

Il determinante di una matrice, che rimane sempre un concetto misterioso

Tempo fa avevo scritto del determinante visto come volume orientato, e di come la sua definizione fosse necessariamente complicata (cioè: se vuoi una formula che funzioni in un certo modo, con determinate proprietà, allora deve essere fatta così).

Possiamo affrontare il problema anche in un altro modo: invece di elencare le proprietà e vedere come va a finire, facciamo il conto una volta per tutte. Lo facciamo in un caso particolare, quello bidimensionale, che riusciamo a visualizzare bene, perché spesso un disegnino spiega più di mille parole (se non sarà una dimostrazione generale da Veri Matematici, pazienza).

Quindi: cosa vogliamo fare? Vogliamo calcolare l'area di un parallelogramma conoscendo i due vettori che lo generano.

Ecco, questa immagine è una dimostrazione senza parole (quasi, via) del fatto che il determinante di una matrice quadrata rappresenta l'area di un parallelogramma generato dai due vettori (a,b) e (c,d), che nel disegno sono scritti in verticale così come si fa di solito in algebra lineare/geometria.

Ecco la spiegazione:

• Il rettangolo blu ha il lato orizzontale lungo a e quello verticale lungo d, quindi la sua area vale ad.
• Trasporto il triangolo rettangolo avente cateti a e b (quello con il tratteggio arancione) in alto.
• Trasporto il triangolo rettangolo avente cateti c e d (quello con il tratteggio viola) a destra.
• Osservo che in questo modo copro tutto il parallelogramma e anche qualcosa in più, e più precisamente il rettangolino in alto a destra, di dimensioni c e b, e quindi di area bc.
• Concludo quindi che l'area del parallelogramma si ottiene sottraendo l'area del rettangolino bc dall'area del rettangolone ad, cioè ad − bc.
• (Noto che devo sottrarre tutto il rettangolino bc e non solo la parte esterna al parallelogramma, perché la parte interna viene contata due volte (e infatti presenta un doppio tratteggio), mentre devo contarla una volta sola)
• Concludo che va tutto bene, quindi l'area del parallelogramma è proprio uguale al determinante della matrice.

Questo disegnino serve anche per capire perché funziona la misteriosa regola di Cramer per risolvere i sistemi lineari, ma questa è un'altra storia.

P.S. Questo è il millesimo post di questo blog. Incredibile.

Uso privato di blog privato

Qualche giorno fa ho partecipato alla Quinta Giornata Nazionale di Analisi Non Standard (sì, c'è gente strana al mondo) e, siccome non sono mica abituato a parlare in pubblico — a gente che ascolta davvero, voglio dire — ero molto nervoso e per questo alla fine del mio intervento ero così provato che, quando una persona è venuta da me a dirmi complimenti professore tirando fuori il mio libro e chiedendomi di firmarglielo, io l'ho fatto quasi meccanicamente, un po' drogato dal fatto che avevo finito di parlare senza aver fatto errori clamorosi e anche dal fatto che qualcuno mi era venuto a cercare col mio libro. Poi, alla fine di tutto, quando ci si saluta e ognuno se ne torna a casa, quella persona è tornata e molto educatamente ha salutato, e io credo di aver detto grazie e arrivederci, ma insomma, non le ho nemmeno chiesto il nome, chi fosse, come mai avesse deciso di partecipare a questa roba non standard.

Ecco, allora, grazie ancora, gentile sconosciuto, e se volesse palesarsi nei commenti mi farebbe molto piacere.

Le terne pitagoriche, spiegate bene — 4. Cosa c'è da dire ancora?

“Non so immaginare cosa ci sia ancora da dire, però fammi vedere qualche altra terna pitagorica oltre a (3,4,5)”.

“Certo. Ti ricordo il teorema:”.

x = 2st
y = s² - t²
z = s² + t²

con s > t > 0, s e t primi tra loro, s e t hanno diversa parità.

“Ricordo”.

“Ed eccoti una tabella, con s minore o uguale di 10”.

  s  t     x   y   z
 -------------------
  2  1 |   4   3   5
  3  2 |  12   5  13
  4  1 |   8  15  17
  4  3 |  24   7  25
  5  2 |  20  21  29
  5  4 |  40   9  41
  6  1 |  12  35  37
  6  3 |  36  27  45
  6  5 |  60  11  61
  7  2 |  28  45  53
  7  4 |  56  33  65
  7  6 |  84  13  85
  8  1 |  16  63  65
  8  3 |  48  55  73
  8  5 |  80  39  89
  8  7 | 112  15 113
  9  2 |  36  77  85
  9  4 |  72  65  97
  9  6 | 108  45 117
  9  8 | 144  17 145
 10  1 |  20  99 101
 10  3 |  60  91 109
 10  5 | 100  75 125
 10  7 | 140  51 149
 10  9 | 180  19 181

“Uh, la prima è proprio (3,4,5)”.

“Sì, ordinata in modo diverso perché abbiamo deciso di chiamare con x il cateto pari”.

“Vero”.

“Ora, avendo scritto un po' di numeri con cui poter giocare, ecco un paio di proprietà. Prima: x è divisibile per 3, oppure y è divisibile per 3”.

“Fammi controllare… sembra vero”.

“Lo è. Però facciamo una dimostrazione, non un controllo su un esiguo numero di terne”.

“Che sono infinite, no?”.

“Appunto, quindi controllarne solo alcune non dimostra nulla”.

“Ok. Come lo dimostriamo?”.

“Se 3 divide x, siamo già a posto, fine del problema”.

“Bé, ma che dimostrazione è?”.

“È un pezzo di dimostrazione, porta pazienza. Primo caso: se 3 divide x, il teorema è già dimostrato e siamo a posto”.

“Ma non è detto che 3 divida x, no?”.

“No, infatti, e questo è il secondo caso: se 3 non divide x vuole dire che non divide né s né t, dato che x = 2st”.

“Ah, ho capito, stai analizzando separatamente i due casi. Il primo è ovvio, il secondo invece mi sembra meno semplice”.

“Certo. Se 3 non divide s e non divide t, come possiamo scriverli in modo tale da mettere in evidenza questa proprietà?”.

“Possiamo dire che s = 3h + 1, per esempio”.

“Molto bene, ma non è l'unica possibilità”.

“Giusto, s potrebbe anche essere uguale a 3h + 2”.

“Certo, ci sono tre possibilità: o un numero è divisibile per 3 (e quindi lo possiamo scrivere come 3h), o ha resto 1 nella divisione per 3 (e lo possiamo scrivere come 3h + 1), o ha resto 2 (e lo scriviamo come 3h + 2). Non ci sono altri casi”.

“Ok. Stessa cosa per t: potrebbe essere 3k + 1 oppure 3k + 2”.

“Giusto. A questo punto calcola s²”.

“In entrambi i casi?”.

“Sì”.

“Allora, nel primo caso, quello in cui s = 3h + 1, se elevo al quadrato ottengo s² = 9h² + 6h + 1”.

“Cosa puoi dire per quanto riguarda la divisione per 3?”.

“Che questo è ancora un numero del tipo 3H + 1, cioè dà ancora resto 1”.

“Perfetto. Controlla l'altro caso”.

“Darà come resto 2”.

“Controlla bene”.

“Mh. Allora, se s = 3h + 2, si ha che s² = 9h² + 12h + 4, quindi è del tipo 3H + 4. No, 4 è troppo, come faccio?”.

“Ricordati che 4 è uguale a 3 più 1”.

“Ah, ma certo, s² = 3H + 4 = 3H + 3 + 1 = 3(H + 1) + 1, cioè 3K+1. È ancora dello stesso tipo!”.

“Già. Hai scoperto che i quadrati di numeri non divisibili per 3 hanno sempre resto 1 nella divisione per 3”.

“Non lo sapevo”.

“Eh, ora possiamo concludere: dato che y è uguale a s² - t², quanto sarà il resto della divisione di y per 3?”.

“Bé, si può scrivere y = (3H + 1) - (3K + 1), quindi y = 3H - 3K. Ehi, y è divisibile per 3”.

“Ecco dimostrata la proprietà: o x è divisibile per 3, oppure lo è y”.

“Bello. Avevi parlato di un paio di proprietà?”.

“Sì, eccone un'altra: in una terna pitagorica primitiva almeno uno tra gli interi x, y e z è divisibile per 5”.

“Ah. Si ragiona allo stesso modo?”.

“Più o meno, sì. Se un numero non è divisibile per 5 puoi scriverlo in quattro modi diversi, a seconda del resto della sua divisione per 5”.

“Esattamente come prima. Se il numero… lo chiamo a, non è divisibile per 5, posso scriverlo così:”.

a = 5h + 1
a = 5h + 2
a = 5h + 3
a = 5h + 4

“Giusto. Ora eleva al quadrato, ma non stare a fare tutti i calcoli. Tieni presente che quando svolgi i calcoli del quadrato di binomio, il quadrato del primo termine contiene 25, mentre il doppio prodotto contiene 5”.

“Ah, vero! Allora la somma dei primi due termini è sempre divisibile per 5, mi rimane da controllare cosa succede al quadrato del secondo termine”.

“Esatto. Scrivi l'elenco dei quadrati dei secondi termini”.

“Sarebbe questo:”.

1
4
9
16

“Giusto. Come si comportano questi numeri nella divisione per 5?”.

“Vediamo… 1 dà resto 1, naturalmente, 4 dà resto 4, 9 dà resto ancora 4, e 16 dà resto 1”.

“Riassunto: il quadrato di un numero non divisibile per 5 dà resto 1 oppure 4 nella divisione per 5”.

“Ok, e adesso?”.

“E adesso abbiamo, come prima, due casi. O z è divisibile per 5…”.

“E abbiamo già dimostrato quello che vogliamo dimostrare”.

“Oppure non lo è. In questo caso il suo quadrato dà resto 1 oppure 4 nella divisione per 5. Se non fossero divisibili per 5 nemmeno x e y, anche i loro quadrati darebbero resto 1 oppure 4”.

“Bene”.

“Ma la somma di x² + y² che resto darebbe?”.

“Ci sono vari casi, non so”.

“Prova a elencarli, non sono tanti. Fai direttamente le somme con i resti”.

“Ho queste possibilità”.

1 + 1
1 + 4
4 + 1
4 + 4

“Giusto. Il primo caso dà un resto di 2, il secondo un resto di 0…”.

“Di cinque! Uno più quattro fa cinque”.

“Ma no, in una divisione per 5 non puoi avere resto 5: il fatto che venga 5 significa semplicemente che il numero è divisibile per 5, cioè il resto è 0”.

“Ah già”.

“Il terzo caso dà ancora 0, e il quarto caso…”.

“Non 8, ma 3”.

“Giusto, 8 - 5 = 3. Quindi la somma dei quadrati di x e y darebbe resto 0, oppure 2, oppure 3 nella divisione per 5, mentre il quadrato di z può solo dare 1 oppure 4”.

“Allora è impossibile che sia x che y e z non siano divisibili per 5, uno almeno deve esserlo”.

“Proprio così”.

“Abbiamo finito?”.

“Sì. Ti faccio solo notare un'ultima proprietà: l'unica terna pitagorica formata da tre numeri consecutivi è la tua amica (3,4,5)”.

“Ah. Dimostriamo anche questo?”.

“No, te lo lascio per esercizio. Basta svolgere i calcoli”.

Le terne pitagoriche, spiegate bene — 3. Come sono fatte?

“Allora, oggi mi dici come sono fatte le terne pitagoriche primitive?”.

“Sì. Vediamo di costruirle pian piano. Abbiamo detto che se vale l'equazione x² + y² = z² allora x è pari, y è dispari, z è dispari”.

“A meno di uno scambio tra x e y”.

“Esatto, è solo una questione di nomi. Il triangolo rettangolo ha due cateti, uno pari e uno dispari. Quello pari si chiama x”.

“Perfetto”.

“Inoltre, in una terna primitiva non ci sono fattori comuni tra x, y e z”.

“Nemmeno se li si prende a due a due”.

“Vero anche questo. Infine, possiamo anche sottolineare il fatto che z è maggiore di y”.

“Certamente, è l'ipotenusa”.

“Quindi z - y è una quantità positiva”.

“Vero anche questo, ma perché me lo dici?”.

“Perché ci serve saperlo tra un attimo. Dato che x² è uguale a z²-y², utilizzando la formuletta della differenza tra due quadrati possiamo scrivere:”.

x² = (z - y)(z + y)

“Ok, ci sono”.

“(z - y) è una quantità positiva, perché z è maggiore di y, come abbiamo detto poco fa”.

“Ah, ecco perché me l'hai fatto notare”.

“E naturalmente anche (z + y) è positiva”.

“Certo”.

“Sono anche entrambe quantità pari”.

“Questo perché…”.

“La somma e la differenza di due numeri dispari danno un numero pari”.

“Giusto”.

“Quindi possiamo indicare (z - y) con 2u e (z + y) con 2v”.

“Va bene, così è evidente che sono numeri pari”.

“E dunque x² = (z - y)(z + y) = 4uv”.

“Fin qua ci sono”.

“Allora (x/2)² sarà uguale a uv.”.

“Va bene, anche se mi piace poco quella frazione”.

“Ma in realtà non è una frazione, perché abbiamo detto che x è pari, quindi stiamo sempre lavorando con numeri interi”.

“Ah, giusto! Ci sono, allora, andiamo avanti”.

“Ragioniamo un momento su questi due numeri u e v. Voglio dimostrare che sono primi tra loro”.

“E come fai?”.

“Intanto ti faccio notare che si possono esprimere in funzione di y e z. Cosa si può ricavare, infatti, da queste due relazioni?”.

z + y = 2v
z - y = 2u

“Cosa si può ricavare?”.

“Se le sommi, ottieni che 2z = 2(v + u), no?”.

“Vero. Quindi z = v + u”.

“E se le sottrai?”.

“Se faccio la prima meno la seconda ottengo 2y = 2(v - u). Quindi y = v - u. Ah, allora z e y si possono esprimere facilmente in funzione di u e v:”.

z = v + u
y = v - u

“Molto bene. Allora possiamo dimostrare quello che abbiamo detto un momento fa: u e v sono primi tra loro perché, se avessero un fattore comune, questo sarebbe comune anche a v + u e a v - u, e di conseguenza sarebbe comune a z e y”.

“Che però devono essere primi tra loro”.

“Esattamente, l'abbiamo dimostrato l'altra volta, è quella che abbiamo chiamato proprietà 3.”.

“E adesso?”.

“Adesso torniamo all'uguaglianza (x/2)² = uv. Abbiamo un prodotto di due numeri primi tra loro che dà come risultato un quadrato, quindi…”.

“Quindi, applicando la proprietà 4, possiamo dire che quei due numeri sono due quadrati!”.

“Perfetto, quindi possiamo indicare u con t² e v con s²”.

“Molto bene”.

“Dato che v - u è uguale a y, numero positivo, questo significa che v è maggiore di u, e quindi che s è maggiore di t”.

“Giusto anche questo”.

“E allora abbiamo finito, ecco come sono fatte le terne pitagoriche:”.

x = 2st
y = s² - t²
z = s² + t²

“Ah, ecco. Un momento, la prima uguaglianza da dove viene?”.

“Bè, avevamo detto che x² = 4uv, cioè 4s²t²”.

“Ah, ok, facciamo la radice. Ma possiamo assegnare a s e t tutti i valori che vogliamo?”.

“No. Abbiamo già detto che s deve essere maggiore di t, perché y deve risultare positivo”.

“Vero”.

“Inoltre s e t devono essere uno pari e uno dispari”.

“Provo a capire perché, ormai ci ho preso la mano… Allora, se fossero entrambi pari, vediamo, la loro somma e la loro differenza sarebbero pari, ma allora y e z sarebbero entrambi pari, e non va bene”.

“Stessa cosa se fossero entrambi dispari, no?”.

“Ah, certo, la somma e la differenza di due numeri dispari sono pari, quindi si fa esattamente lo stesso ragionamento”.

“Infine: è possibile che s e t abbiano fattori comuni?”.

“No, questo è facile: se li avessero li avrebbero anche x, y e z”.

“Benissimo. Questo è il teorema, che non è ancora completo però”.

“Cosa manca?”.

“Il viceversa. Cioè adesso abbiamo detto che se abbiamo una terna pitagorica allora la si può scrivere in funzione di s e t come detto poco fa. Viceversa, dati s e t con le caratteristiche dette sopra, è sempre vero che generano una terna pitagorica?”.

“Ah. Boh, e come si fa a saperlo?”.

“Qui è facile, si fa il calcolo. È vero che x² + y² = z²? Prova a calcolarlo”.

“Allora, x² sarebbe 4s²t², mentre y² sarebbe s⁴ - 2s²t² + t⁴. Se li sommo ottengo s⁴ + 2s²t² + t⁴”.

“Che, guarda un po', è proprio il quadrato di z”.

“Ah, bene, allora abbiamo finito”.

“Quasi”.

“Ma come? Cosa c'è ancora?”.

“Eh, quella che hai ottenuto è effettivamente una terna pitagorica, l'hai appena dimostrato. Ma è anche primitiva?”.

“Uffa. Allora, vediamo, se x, y e z avessero un fattore comune…”.

“Chiamalo p, e supponi che sia primo”.

“Se avessero un fattore comune avrebbero anche un fattore primo comune, lo chiamo p, ok”.

“Questo p dovrebbe dividere anche z + y”.

“Certo”.

“E z + y è uguale a 2s²”.

“Fammi controllare… ok, giusto, basta sommarli”.

“E ragionando allo stesso modo, p dovrebbe dividere anche z - y”.

“Giusto. Ti anticipo dicendo che z - y è uguale a 2t²”.

“Perfetto. E osserva anche il fatto che p non è uguale a 2”.

“Uh, allora, p non è 2 perché…”.

“Perché divide x e anche y, ma uno è pari e uno è dispari”.

“Giusto”.

“Quindi p divide 2s², p divide 2t², p non è 2”.

“E allora p dividerà s² e t²”.

“E dunque, siamo alla fine, p divide s e anche t. Ma s e t erano…”.

“Primi tra loro! Impossibile! Ah, finalmente, abbiamo dimostrato che quella è davvero la formula per ottenere tutte e sole le terne pitagoriche”.

“Te la riassumo qua sotto:”.

---

Tutte e sole le terne pitagoriche primitive con x pari sono date dalle formule seguenti:

x = 2st
y = s² - t²
z = s² + t²

con s > t > 0, s e t primi tra loro, s e t hanno diversa parità.

---

“Uff. Finito?”.

“Sì. Bé, la prossima volta concludiamo con qualche proprietà poco nota, e poi magari scriviamo anche qualche terna diversa dalla solita (3,4,5)”.

“Molto bene”.

Le terne pitagoriche, spiegate bene — 2. Che proprietà hanno?

“Allora, mi hai detto che in una terna pitagorica i due cateti sono uno pari e uno dispari”.

“Esatto. Da adesso in poi diciamo che quello pari sia quello che abbiamo indicato con x, e quindi quello dispari è y”.

“E z?”.

“Proviamo a capire se c'è anche qualche proprietà che riguarda z. Può essere pari?”.

“Eh, boh, devo provare”.

“Prova. Ricordati che l'equazione x² + y² = z² può anche essere scritta come y² = z² - x²”.

“Ah, allora se sia x che z sono pari, dovrebbe esserlo anche y”.

“Che invece è dispari”.

“Allora è impossibile che z sia pari, quindi deve essere sempre dispari”.

“Benissimo, ecco una nuova proprietà:”.

Proprietà 2: in una terna pitagorica primitiva, x è pari, y è dispari, z è dispari (a meno di uno scambio tra x e y)

“Molto bene”.

“Ora, è possibile che i due termini y e z abbiano fattori in comune?”.

“Se ce li hanno, devono essere dispari”.

“Giusto. Inoltre, se ce li hanno, li possiamo scomporre e possiamo così affermare che esiste un numero primo p che li divide entrambi”.

“Certo”.

“E quindi p divide anche i loro quadrati”.

“Senza dubbio”.

“E allora p deve dividere anche il quadrato di x, perché x² = z² - y²”.

“Ma allora p li dividerebbe tutti e tre, e questo è impossibile, perché abbiamo a che fare con terne primitive”.

“Forse x e y potrebbero avere qualche fattore comune, allora?”.

“Mah, mi sembra che si possa ripetere il ragionamento appena fatto. Non serviva sapere che y e z fossero dispari”.

“Esatto. Quindi nemmeno x e z possono avere fattori comuni, giusto?”.

“Giusto. Ecco una nuova proprietà:”.

Proprietà 3: in una terna pitagorica primitiva, MCD(x,y) = MCD(x,z) = MCD(y,z) = 1

“Che è un modo complicato per dire che nemmeno presi a coppie x, y e z hanno fattori comuni”.

“Proprio così. Ora vediamo un'ultima proprietà, che è abbastanza semplice da raccontare, ma un po' noiosa da dimostrare alla maniera dei Veri Matematici”.

“Uhh”.

“Eccola:”.

Proprietà 4: Se il prodotto di due numeri primi tra loro è un quadrato, allora i due numeri sono due quadrati

“Mh”.

“Il prodotto di due numeri primi tra loro è 36, che è un quadrato. Quali sono questi due numeri?”.

“Sei e sei. Sei per sei fa trentasei. Ma sei non è un quadrato, qualcosa non va”.

“Certo che qualcosa non va: sei e sei non sono primi tra loro”.

“Ah, ehm, vero”.

“I due numeri corretti sono 4 e 9, che sono due quadrati”.

“Già”.

“Questo vale sempre”.

“Ed è difficile da dimostrare?”.

“No, è noioso perché devi sempre pensare alle scomposizioni in fattori primi dei numeri, e allora le formule da scrivere sono lunghe perché non sai mai a priori in quanti fattori sia scomponibile un numero. Comunque, vediamo un'idea di dimostrazione. Indichiamo con a e b i due numeri che, moltiplicati, danno un quadrato, che indichiamo con c²”.

“Ok, ab = c²”.

“Succede che a sarà scomponibile in fattori, così come b”.

“Certo”.

“Dato che a e b sono primi tra loro, i fattori della scomposizione di a saranno diversi da quelli della scomposizione di b”.

“Ok”.

“E quindi i fattori di ab saranno tutti quelli di a assieme a tutti quelli di b”.

“Giusto”.

“Ma tutto questo è uguale a c², che sarà pure lui scomponibile in fattori. Ma è un quadrato…”.

“Quindi nella sua scomposizione ci saranno tanti fattori al quadrato”.

“Questo è il punto. Dato che il teorema fondamentale dell'aritmetica ci dice che la scomposizione in fattori primi è unica, la scomposizione in fattori di ab deve essere uguale a quella di c²”.

“Ah, allora ci saranno quadrati anche nella scomposizione di a e b”.

“Ed ecco fatto: anche a e b sono quadrati. Te lo faccio capire meglio con un esempio: il prodotto ab = 8100, che è il quadrato di 90. Prova a scomporlo:”.

“Dunque, 8100 è 2²3⁴5². Come faccio a sapere chi sono a e b?”.

“Fai i vari casi, ma ricordati che devono essere primi tra loro”.

“Allora, potrei avere a = 2² e b = 3⁴5²”.

“E sia a che b sarebbero due quadrati”.

“Vero. Oppure potrei avere a = 2²3⁴ e b = 5²”.

“E anche in questo caso hai due quadrati”.

“Ah, ma ho capito, si hanno sempre quadrati. L'unico modo per non averli sarebbe quello di spezzare le potenze distribuendole un po' su a e un po' su b”.

“Ma non si può, perché a e b devono essere primi tra loro”.

“Ok, ho capito. E adesso?”.

“Adesso costruiamo queste benedette terne”.

Le terne pitagoriche, spiegate bene — 1. Cosa sono?

“Ahh, i bei tempi in cui si poteva giocare”.

“Eh?”.

“Ma sì, me lo vedo Pitagora, nei pomeriggi di Natale, intorno alla tavola assieme ai suoi soci, con il nonno che estraeva i numeri, tre!, quattordici!, quindici!, e Pitagora che urlava terna!, e Ippaso invece tombola!, e Pitagora si arrabbiava sempre, e poi si sa che fine ha fatto Ippaso…”.

“…”.

“E allora Pitagora voleva cambiare gioco, dai mettiamoci a suonare un po' la lira, sentite come vibrano bene queste corde, Ippaso smettila che sei stonato, e gli altri basta Pitagora ci hai rotto con le tue corde che suonano, ma una bella batteria quando la mettiamo su, che noia questa musica, e se sei sfortunato alla tombola non è mica colpa nostra…”.

“ALLORA”.

“Ehm”.

“NO, DICO”.

“Erano altre terne quelle di cui volevi parlare, vero?”.

“Già”.

“Forse quelle del teorema di Pitagora, vero?”.

“Eh”.

“Il quadrato costruito sull'ipotenusa di un triangolo rettangolo è equivalente alla somma dei quadrati costruiti sui cateti”.

“Così andiamo meglio. Se vogliamo tradurre in formule, x² + y² = z²”.

“Dove x e y sono i cateti e z invece è l'ipotenusa, vero?”.

“Certo. Per terna pitagorica si intende una terna di numeri naturali che soddisfa quell'equazione”.

“La famosa terna 3, 4 e 5. Mi ricordo solo quella…”.

“Quella è un esempio, ma ce ne sono altre. Tante altre. Naturalmente se trovi una terna di numeri interi che va bene, puoi anche cambiare qualche segno e quello che ottieni soddisfa ancora l'equazione, perché tanto elevi tutto al quadrato e i segni si perdono”.

“Anche se non ha significato geometrico”.

“Infatti. Noi ragioniamo sui numeri positivi per non avere problemi di segno”.

“Ok”.

“Allora, la domanda è: come sono fatte queste terne? Che proprietà hanno? Come si trovano?”.

“Boh?”.

“Una prima proprietà che possiamo notare subito (e che conoscono anche gli studenti delle medie, quando risolvono problemi che si basano sulle terne pitagoriche) è questa: data una terna che soddisfa l'equazione x² + y² = z², ne possiamo trovare infinite altre moltiplicando tutti i termini della terna per un fattore comune”.

“Cioè mi stai dicendo che se va bene la terna (3,4,5) allora va bene anche la terna (6,8,10)? Mh, sì, in effetti è vero, il fattore comune viene elevato al quadrato e lo si può semplificare”.

“Esattamente, se (x,y,z) soddisfa all'equazione del teorema di Pitagora, allora lo fa anche la terna (dx,dy,dz), perché risulta d²x² + d²y² = d²z²”. Dividendo tutto per d² ritrovi l'equazione iniziale.

“Ok, chiaro. Quindi in sostanza ci interessano le terne non semplificabili”.

“Sì, che vengono dette terne pitagoriche primitive, e sono tali per cui il massimo comun divisore tra x, y e z è uguale a 1”.

“Cioè sono non semplificabili, come ho detto io”.

“Io ho usato il linguaggio che usano i Veri Matematici”.

“Che sono abituati a complicare le cose semplici”.

“Ma no, sono solo precisi”.

“Ma smettila… Allora dobbiamo capire come sono fatte queste terne primitive?”.

“Sì, vediamo una prima proprietà. Diamo sempre per scontato che x e y siano le lunghezze dei due cateti, mentre z è l'ipotenusa. Domanda: x e y possono essere entrambi numeri pari?”.

“Boh? No, hai detto che devono essere primi tra loro”.

“No. L'affermazione che hai appena detto tu è diversa: io ho detto che x, y e z devono essere primi tra loro, ma è possibile che x e y abbiano fattori comuni. In realtà vedremo dopo che non è così, ma adesso non lo sappiamo ancora”.

“Ah, ok. Come faccio allora a sapere se x e y possono essere entrambi pari?”.

“Prova: se sono entrambi pari come saranno i loro quadrati?”.

“Pari pure loro”.

“Puoi dire di più: sono divisibili per il quadrato di 2, cioè sono multipli di 4”.

“Giusto”.

“E dall'equazione x² + y² = z² puoi immediatamente dedurre che anche il quadrato di z deve essere divisibile per 4…”.

“E quindi z deve essere pari, ma questo non è possibile, perché stiamo studiando le terne primitive! In questo caso invece avremmo tre numeri pari, e non va bene”.

“Molto bene. Possono essere entrambi dispari?”.

“Eh, uhm, qui non so mica rispondere, se sono dispari non vuole dire che abbiano un fattore comune”.

“Vero. Se sono dispari li puoi scrivere in questo modo: x = 2h + 1, y = 2k + 1”.

“D'accordo, i numeri dispari si possono scrivere così. È come dire che sono uguali a un numero pari più uno”.

“O, se vuoi usare l'aritmetica modulare, è come dire che sono congruenti a 1 modulo 2. Insomma, il resto della divisione per 2 è uguale a 1. Quando elevi al quadrato, il resto della divisione per 2 sarà ancora 1”.

“Che è un modo complicato per dire che il quadrato di un numero dispari è dispari. Se non c'era un fattore 2 prima di elevare al quadrato, non c'è nemmeno dopo”.

“Perfetto. Cosa mi dici allora della somma dei due quadrati dispari?”.

“Dispari più dispari fa pari”.

“Bene, ma rispetto alla divisione per 4? Quanto vale il resto della divisione per 4 di un dispari più un altro dispari?”.

“Boh?”.

“Dobbiamo fare il calcolo. Eleva al quadrato (2h + 1)”.

“Col quadrato del binomio?”.

“Certo”.

“Viene 4h² + 4h + 1… ah, forse ho capito. È un numero che si può scrivere come 4H + 1”.

“Molto bene”.

“Quindi il quadrato di un numero dispari dà resto 1 nella divisione per 4. Bello”.

“E se sommi due quadrati di dispari, cioè due numeri del tipo 4H + 1 e 4K + 1?”.

“Ottengo 4(H + K) + 2, quindi z² dovrebbe essere un numero che, nella divisione per 4, mi dà resto 2”.

“E questo è impossibile”.

“Perché?”.

“Perché l'abbiamo appena visto: se un numero è pari, il suo quadrato è divisibile per 4, e quindi il resto della divisione per 4 è 0. Se è dispari, il resto è 1. Non ci sono altre possibilità, è impossibile che un quadrato abbia resto 2 nella divisione per 4”.

“Ahh. Ma allora se x e y non possono essere entrambi pari o entrambi dispari, vorrà dire che saranno uno pari e uno dispari”.

“Certo, è rimasta solo questa possibilità. E almeno una volta è verificata, la terna (3,4,5) esiste”.

“Bello”.

“Ok, riassumiamo quindi quello che abbiamo stabilito:”.

Proprietà 1: in una terna pitagorica primitiva x e y sono uno pari e uno dispari.

“Bene”.

“E, come bonus, abbiamo anche scoperto che il quadrato di un numero è sempre congruente a 0 oppure a 1 modulo 4”.

Poi uno chiede perché a scuola ci si ferma al secondo grado

(Via smoot)

Di altalene, molle e vasche da bagno — risonanza

“Il bimbetto dell'altra volta, quello che voleva essere spinto sull'altalena, dopo un po' si è scocciato e ha cominciato a giocare con la terra e il fango”.

“Ottimo”.

“A un certo punto è ora di andare a casa, verso la quale lo trasciniamo perché naturalmente lui vorrebbe stare ancora in mezzo alla terra fino a che non è tutta finita”.

“Benissimo”.

“E, necessariamente, deve farsi il bagno”.

“Oh, finalmente parliamo di vasche da bagno. O lo mettiamo sotto la doccia?”.

“Eh, questa volta vasca”.

“Ottimo”.

“Mentre la vasca si riempie il bimbo si prepara per entrare, raccattando tutti i giochi che gli sono necessari per questa importante attività”.

“Certamente”.

“Poi mette una mano dentro l'acqua, e sente che è troppo calda”.

“Aggiungiamone di fredda, allora”.

“Lo facciamo, ma dopo un po' il bimbo ancora si lamenta perché, con la sua manina, sente ancora caldo nella zona lontana dal rubinetto”.

“Mescolala un po', santo cielo”.

“Hai pronunciato le parole magiche, e il bimbetto si mette a mescolare. Mescolando mescolando, si accorge che riesce a produrre delle belle onde che attraversano la vasca in tutta la sua lunghezza”.

“Oh oh”.

“Queste onde accarezzano la sua mano, che si fa trasportare avanti e indietro, avanti e indietro…”.

“Ahi”.

“Il bimbo, naturalmente, non se ne sta fermo, e anche lui accarezza le onde, a ritmo”.

“Disastro!”.

“Improvvisamente, dopo un ultimo leggero colpetto della mano innocente, si alza uno tsunami che vuota mezza vasca e allaga il pavimento”.

“È successo anche a me da piccolo, coff coff”.

“Credo che sia successo a tutti. Una esperienza divertente, se non fosse per le conseguenze”.

“Ehm”.

“La dura vita dello scienziato: a volte sperimenti senza sapere come andrà a finire”.

“Povero bimbo”.

“Ma proviamo a capire cosa è successo: il bimbo non ha tanta forza da vuotare mezza vasca con una sola manata”.

“Certamente no”.

“E quindi?”.

“Eh, mi sa che ha spinto al momento giusto: questa volta è riuscito ad andare a tempo”.

“Esattamente. Anche questo è un oscillatore forzato smorzato, con una grossa differenza: la frequenza con cui la forza esterna agisce sull'acqua è quella giusta. La piccola quantità di energia che il bimbo fornisce all'acqua contribuisce sempre a aumentare l'ampiezza delle onde della vasca. E a forza di piccoli trasferimenti…”.

“… arriva l'onda anomala”.

“Esatto. Nel caso più semplice di tutti, cioè quello dell'oscillatore senza attriti, non ci sono perdite di energia, mentre tutta l'energia proveniente dall'esterno contribuisce soltanto ad aumentare l'ampiezza delle oscillazioni. Quella modulazione che avevi notato prima ora è in sincronia con le oscillazioni proprie del sistema, che teoricamente potrebbero aumentare di ampiezza all'infinito. Questo è il fenomeno della risonanza”.

“Uh, aumenta sempre di più”.

“Sì, dopo una fase transitoria iniziale, l'oscillazione si stabilizza in frequenza e aumenta sempre di più in ampiezza”.

“Ho capito. Però in realtà non esistono oscillatori senza attriti, no?”.

“In realtà un po' di dispersione c'è sempre, infatti. In questo caso non si verificherà una risonanza pura come quella di questo esempio, in cui l'ampiezza cresce infinitamente: quello che si osserva, e che ha osservato anche il bambino, è che se si verificano opportune condizioni l'ampiezza aumenta molto”.

“Quanto?”.

“Eh, non si può dire a priori: dipende da quanto è l'attrito e quanto è la frequenza propria del sistema. In ogni caso: quanto basta per allagare un bagno”.

“Già”.

“Qui sotto puoi giocare con un oscillatore. Hai tre parametri che puoi modificare:

• k rappresenta la forza di attrito: se lo poni uguale a zero, hai un oscillatore senza attriti,
• a è l'ampiezza della forza esterna: se lo poni uguale a zero hai un oscillatore non forzato,
• b rappresenta invece la frequenza della forza esterna: se trovi il valore giusto puoi fare le onde nella vasca da bagno.

Attento a non allagare”.

Di altalene, molle e vasche da bagno — oscillazioni forzate

“Aggiungiamo alla nostra altalena uno che spinge”.

“Oh, bene”.

“Come sai, se non spingi l'altalena nel modo giusto non ti diverti”.

“Eh, sì. I bimbi piccoli chiedono sempre di essere spinti perché non sono capaci di tenere il tempo”.

“Tenere il tempo è proprio l'espressione giusta, infatti. Il fatto è che un'altalena, e più in generale un oscillatore, ha una sua frequenza di oscillazione”.

“In che senso?”.

“Nel senso che non puoi decidere tu il modo in cui oscilla”.

“Ma io posso decidere se andare più forte o più lentamente!”.

“Certo, ma non puoi decidere la durata di ogni oscillazione. Questo fenomeno si chiama isocronismo del pendolo, una scoperta fatta da Galileo”.

“Ah”.

“In realtà è una legge che vale se le oscillazioni sono abbastanza piccole, se sono troppo grandi non è più vera, ma se lasciamo perdere questo piccolo particolare possiamo dire che tutti gli oscillatori si comportano in questo modo: la frequenza delle oscillazioni non è legata alla loro ampiezza. Vale anche per le corde della chitarra, per esempio”.

“Uh?”.

“Ogni corda emette, oscillando, una nota. Se tu pizzichi la corda con più o meno forza, ottieni solo un cambiamento nel volume della nota, cioè nell'ampiezza dell'oscillazione. Ma la nota rimane sempre quella”.

“Ah, giusto. Ma quindi tu mi stai dicendo che se metto un bambino su un'altalena, oppure se ci salgo io, entrambi andiamo alla stessa velocità?”.

“Non velocità: frequenza. Entrambi battete il tempo allo stesso modo: se tu spingi più forte significa che vai più in alto, con maggiore velocità. Le due cose si compensano: sei più veloce ma devi fare più strada; del resto, gli orologi a pendolo si basano su questo principio.”.

“Pure!”.

“Pure loro, sì. Il pendolo batte sempre il tempo alla stessa frequenza, sia che oscilli molto sia che oscilli poco. In realtà lo si fa oscillare poco perché, come dicevamo prima, per i pendoli questa legge non è del tutto esatta. Se l'angolo di oscillazione cresce molto, non è più vera”.

“E quindi come si fa a regolare un orologio a pendolo?”.

“Si cambia la lunghezza: gli orologi a pendolo hanno un contrappeso in fondo che può essere spostato verso l'alto o verso il basso. In questo modo modifichi la posizione del baricentro e, sostanzialmente, ottieni un pendolo più o meno lungo. Le oscillazioni dipendono solo dalla lunghezza del pendolo”.

“Ah”.

“In realtà dipendono anche dal valore dell'accelerazione di gravità del pianeta su cui il pendolo oscilla, ma direi che possiamo pensare di stare con i piedi per terra”.

“Sono d'accordo”.

“Torniamo allora alla nostra altalena, spinta da qualcuno che non conosce la frequenza di oscillazione”.

“Ma nessuno conosce la frequenza di oscillazione delle altalene!”.

“Vero, ma appena ci sali sopra, o ti metti a spingerla, ti accorgi del modo giusto di farlo, se hai fatto un po' di pratica da bambino”.

“Ah, questo è vero”.

“Ecco, supponiamo che qualcuno che non ha mai visto un'altalena voglia spingerla con una certa frequenza decisa da lui, che non è quella giusta. Che succede?”.

“Boh? Immagino che chi spinge faccia molta fatica a farlo”.

“Sicuramente, perché si troverà spesso fuori sincrono con le oscillazioni, per cui a volte spinge mentre l'altalena va indietro”.

“Deve stare attento a non farsi del male”.

“Pensa a quello che fa un bambino piccolo le prime volte in cui sale su un'altalena: si siede e comincia a muovere all'impazzata le gambe avanti e indietro. Che succede all'altalena?”.

“Niente”.

“Bé, non proprio niente”.

“Sì, va bene, un pochino si muove”.

“Esatto: un pochino oscilla avanti e indietro, seguendo il moto dato dal bimbo, ma senza quelle belle oscillazioni che il bimbo vorrebbe”.

“Già”.

“E che succede se tu gli dai una spinta, all'inizio, e poi lo lasci andare?”.

“Eh, succede che l'altalena oscilla un pochino, e pian piano si smorza”.

“Bene, hai descritto perfettamente il comportamento di un oscillatore forzato e smorzato”.

“Forzato?”.

“Sì, con uno che spinge, insomma. C'è una forza esterna che imprime una oscillazione”.

“Ah. Ma non ho ben capito cosa ho descritto…”.

“Hai descritto questo: l'oscillatore ha una sua frequenza di oscillazione, che pian piano si smorza a causa dell'attrito. Quello che rimane è dovuto soltanto alla forza esterna, che oscilla a una frequenza che non è quella giusta e che, quindi, provoca soltanto piccoli movimenti”.

“Ma la forza esterna c'è anche all'inizio, quando l'oscillatore è ancora in grado di oscillare secondo la sua frequenza propria, no?”.

“Certo: i due tipi di oscillazione sono sempre presenti; all'inizio, però, prevale l'oscillazione propria (cioè prevale la grossa spinta che dai all'altalena in modo da fare divertire il bimbo che non è capace di spingersi), e in seguito prevale l'oscillazione forzata (cioè il bimbo che sgambetta e fa oscillare di poco l'altalena). Eccoti un disegno di esempio”.

“Ah, ecco, sembra una modulazione”.

“Lo è! L'oscillazione smorzata dell'altalena viene modulata dalle piccole oscillazioni impresse dal bimbo. Alla fine rimangono solo quelle e il bimbo si scoccia”.

“Bello. Questo comportamento si verifica anche nel caso dell'altalena arrugginita?”.

“Quello della modulazione? Sì. Naturalmente nel caso dell'altalena arrugginita non c'è nemmeno una qualche oscillazione iniziale e quindi il bimbo si scoccia subito”.

“E quand'è che insegniamo al bimbo ad andare in altalena?”.

“La prossima volta”.

“Con anche la vasca da bagno?”.

“Con anche la vasca da bagno”.

Di altalene, molle e vasche da bagno — oscillazioni

“Parliamo di altalene meno arrugginite, oggi?”.

“Sì. Tutto è come prima, ma c'è meno attrito. Tu sali sull'altalena, ti lasci andare, man mano che scendi vieni sottoposto a una forza sempre più piccola, come succedeva prima, con una importante differenza”.

“La forza è sempre più piccola, ma non troppo piccola”.

“Esatto. La forza ti permette di arrivare in un tempo finito alla posizione più bassa dell'altalena, e con ancora abbastanza velocità da poter salire dall'altra parte”.

“Un po' meno in alto rispetto alla quota dalla quale ero partito, però”.

“Esatto, perché l'attrito ti fa perdere un po' di energia. Però, dato che riesci a risalire dall'altra parte, poi puoi tornare indietro, e di nuovo passi dalla posizione più bassa con ancora abbastanza velocità da poter risalire dall'altra parte”.

“E così via”.

“E così via. E questo, in matematica, significa che oscillerai per sempre, con ampiezza sempre più piccola”.

“Ma in pratica dopo un po' mi fermerò, no?”.

“Sì, nel mondo fisico a un certo punto non apprezzi più nessuna oscillazione, mentre dal punto di vista matematico puoi pensare a oscillazioni di ampiezza sempre più piccola, ma non nulla”.

“Ok”.

“Ti faccio vedere il grafico anche di questo secondo caso, eccolo”.

“Bello, oscillazioni sempre più piccole”.

“Questo viene detto moto oscillatorio smorzato, o sottosmorzato”.

“Perché è smorzato troppo poco, giusto? Mentre l'altalena arrugginita era sovrasmorzata”.

“Esatto”.

“E il terzo caso, quindi? Sarebbe una via di mezzo tra il moto sottosmorzato e quello sovrasmorzato?”.

“Proprio così, lo smorzamento del caso rimanente si chiama smorzamento critico. Sarebbe quello di un'altalena che ha la giusta quantità di attrito per non farti oltrepassare lo zero, ma non di più. Non ti frena troppo, ma neanche troppo poco”.

“Mi frena il giusto, insomma”.

“Sì, ti fa arrivare in fretta alla posizione più bassa, ma non troppo in fretta. Mh, in realtà non sono stato preciso: anche in questo caso alla posizione di riposo ci arrivi in un tempo infinito, però scendi più velocemente rispetto a quello che facevi prima. Ma se scendessi con una velocità ancora superiore, anche se di pochissimo, passeresti dall'altra parte e cominceresti a oscillare. Ecco il disegno”.

“Mi sembra uguale al primo caso”.

“No, in realtà questo moto scende più velocemente. Guarda, te li sovrappongo sulla stessa figura”.

“Ah, ecco, ora è chiaro”.

“Il mio prof di fisica diceva che, quando devi tarare gli ammortizzatori di un'automobile, devi cercare lo smorzamento critico. Se le molle sono troppo dure, sei nel caso sovrasmorzato e l'auto si adatta male alle buche, e chi è a bordo sente troppi contraccolpi. Viceversa, nel caso sottosmorzato l'auto comincia a oscillare e a chi è a bordo viene il mal di mare”.

“Bello, ho capito. Mi manca un'ultima cosa, però”.

“Cosa?”.

“La vasca da bagno”.

“Porta pazienza”.

Di altalene, molle e vasche da bagno — attriti

“Vasche da bagno?”.

“E altalene, e molle”.

“E cosa c'entrano con la matematica?”.

“A parte il fatto che, volendo, tutto c'entra con la matematica, in questo caso parliamo di un fenomeno preciso: le oscillazioni”.

“Quindi parliamo di fisica”.

“Eh, dipende dal punto di vista: la matematica fa da modello per i fenomeni fisici, oppure è l'alfabeto nel quale Dio ha fcritto l'univerfo?”.

“…”.

“Ma non addentriamoci in queste questioni filosofiche”.

“Ecco, meglio”.

“Parliamo di equazioni matematiche che vengono usate in fisica per studiare le oscillazioni, e lo facciamo ponendo l'accento sulla parte matematica, senza però tralasciare riferimenti alla vita quotidiana”.

“Come la vasca da bagno”.

“Esatto”.

“Cosa c'entra, poi, la vasca da bagno?”.

“Vedrai, vedrai. Ma partiamo dall'inizio: in fisica esistono fenomeni oscillatori di tanti tipi, da quelli generati dai circuiti elettrici che vengono usati, tanto per fare un esempio, in tutti i nostri dispositivi wi-fi alle oscillazioni prodotte da una massa collegata a una molla, o quelle di un pendolo, o di un'altalena”.

“Ok”.

“E il bello è che le equazioni che descrivono questi fenomeni sono sempre le stesse: cambiano certamente le grandezze in gioco e le unità di misura, ma la forma dell'equazione è quella. Che siano elettroni che si muovono lungo un conduttore, o masse sottoposte alla forza di gravità, o a forze elastiche, si ha sempre a che fare con lo stesso tipo di equazione”.

“Che sarebbe?”.

“Eh, purtroppo è un'equazione complicata: i Veri Matematici la chiamano equazione differenziale”.

“Roba di cui non ho assolutamente idea”.

“E che non cerco di spiegarti adesso: servono troppe conoscenze matematiche per farti vedere come si può risolvere. Posso però cercare di darti un'idea intuitiva”.

“Proviamo”.

“In questo tipo di equazioni l'incognita non è un numero, ma una funzione”.

“Uhm”.

“La funzione che ti dà la posizione, istante per istante, del pendolo, o dell'altalena, o della massa attaccata alla molla, o della quantità di carica elettrica che attraversa un filo conduttore”.

“Ah”.

“Inoltre, questo tipo di equazioni contiene informazioni sul modo in cui varia la funzione incognita, e questo è il difficile”.

“Infatti non ho capito niente”.

“Pensa a una molla fissata in terra, e a te che ci sali sopra”.

“Bene, come un tappeto elastico”.

“Esattamente. L'incognita è la posizione dell'estremo della molla che si muove”.

“Quello attaccato a me, insomma?”.

“Esatto”.

“E perché è una funzione?”.

“Perché la posizione non è fissa, ma dipende dal tempo”.

“Ah, ok”.

“Ora pensa a quello che succede: se tu sali sulla molla, questa si comprime”.

“Giusto”.

“Ma comprimendosi esercita una forza verso l'alto, cioè verso di te”.

“Anche questo è vero”.

“E allora l'effetto della tua salita sulla molla sarà un po' mitigato da questa forza contraria”.

“Giusto”.

“E quindi la tua azione di compressione sarà meno efficace, e la molla farà sempre più fatica a accorciarsi”.

“Sì, è così, infatti non la posso comprimere all'infinito, a un certo punto mi bilancerà”.

“Benissimo. Il fatto interessante è che questa azione di bilanciamento non si manifesta all'improvviso: man mano che comprimi la molla senti una forza contraria sempre più grande che ti impedisce di comprimerla con la stessa intensità. Insomma, la velocità con cui la molla si comprime varia nel tempo, fino a che non si arriva alla massima compressione. Anzi, può succedere che tu venga poi spinto via, cioè verso l'alto”.

“Come succede effettivamente nei tappeti elastici”.

“Certo. L'equazione che descrive questo comportamento tiene conto di tutto: cioè tiene conto della tua posizione e del fatto che più comprimi, maggiore è la forza esercitata dalla molla su di te. Forza che a sua volta produce una variazione nella tua velocità”.

“Uh, complicato”.

“Eh, sì. Si dice che un'equazione differenziale dà una descrizione locale di un fenomeno”.

“Locale?”.

“Locale in senso matematico, cioè in questo caso circoscritta a un istante di tempo. In sostanza ti dice: guarda che adesso le leggi che governano il tuo moto sono queste, ma tra un po' saranno diverse perché la molla non sarà più nella stessa posizione e quindi eserciterà una forza diversa su di te”.

“Una roba del tipo adesso la molla spinge poco, tra un po' spingerà di più, e così via?”.

“Più o meno… Quello che ti dice l'equazione è ciò che succede istante per istante, quello che devi fare tu per risolverla è ricostruire il comportamento globale. È come se tu fossi all'interno di un'automobile con i vetri oscurati, assieme a un navigatore che ti dice, istante per istante, che strada devi prendere. Tu, oltre a fidarti delle indicazioni, devi ricostruire il percorso”.

“Ah, bello, così ho quasi capito”.

“Bene, mi fa piacere. Allora, risolvendo l'equazione si possono verificare tre casi, che adesso provo a descriverti”.

“Vai”.

“Il primo caso è quello senza oscillazioni”.

“Ma come?”.

“Eh, ricordi che ti ho parlato di altalene?”.

“Certo, quelle oscillano”.

“Non sempre: immaginati un'altalena molto arrugginita”.

“…”.

“Dico sul serio: immagina che ci sia una grande forza di attrito. Puoi immaginarti un'altalena arrugginita, oppure una molla che fa strisciare un corpo molto rugoso e pesante sul pavimento”.

“Uhm”.

“A fatica sollevi il seggiolino dell'altalena, ti ci siedi sopra, e ti lasci andare. Con un grande cigolio di cardini pian piano scendi verso il basso, ma sempre più lentamente”.

“Prima o poi arrivo in fondo”.

“Dal punto di vista fisico, in una situazione reale, prima o poi ci arrivi. Nel nostro modello matematico la tua velocità diminuisce sempre di più man mano che scendi, in modo tale che ti ci vorrebbe un tempo infinito per arrivare in basso”.

“Ah”.

“Ora provo a farti vedere un disegno: sull'asse orizzontale metto il tempo, sull'asse verticale invece metto l'angolo che l'altalena forma con una immaginaria retta verticale che rappresenta la condizione di riposo”.

“Uh, tutto qua?”.

“Eh, sì, un'altalena arrugginita non è tanto divertente”.

“Cosa rappresentano i numeri sugli assi?”.

“Niente di speciale, immagina delle unità di misura arbitrarie, scelte per comodità. Quello che conta è che la posizione dell'altalena si avvicina molto lentamente allo zero”.

“E più si avvicina, più è lenta, giusto?”.

“Esatto, è proprio così, questo è quello che dice l'equazione differenziale. Più sei vicino alla posizione verticale, più sei lento negli spostamenti”.

“Ho capito. Ma questo è uno solo dei tre casi, vero?”.

“Sì, è quello che viene detto moto aperiodico smorzato, o sovrasmorzato”.

“In pratica, c'è troppo attrito, niente oscillazioni”.

“Esatto”.

“E gli altri due casi?”.

“Li vediamo la prossima volta”.

Trucchi matematici per le vostre serate mondane

Come elevare al quadrato un numero di due cifre

Ricordando il famoso prodotto notevole (a + b)² = a² + 2ab + b² (e cioè quadrato del primo più doppio prodotto del primo per il secondo più quadrato del secondo), si può elevare al quadrato a mente in questo modo:

• si calcola il quadrato della cifra delle unità, e si scrive la cifra delle unità del risultato (le decine vanno a riporto)
• si calcola il doppio prodotto della cifra delle unità per la cifra delle decine, si somma l'eventuale riporto, e si scrive la cifra delle unità alla sinistra della cifra scritta al punto precedente
• si calcola il quadrato della cifra delle decine, si somma l'eventuale riporto, e si scrive i risultato a sinistra delle due cifre scritte prima

Funziona perché un numero avente come cifra delle decine a e come cifra delle unità b può essere scritto come (10a + b) e quindi, elevandolo al quadrato, si ottiene:

(10a + b)² = 100a² + 20ab + b²,

da cui si deduce che la cifra delle unità è quella di b², quella delle decine è data da 2ab più l'eventuale riporto della cifra delle unità, e quella delle centinaia da a² più l'eventuale riporto della cifra delle decine.

Esempio, vogliamo calcolare il quadrato di 42:

• 2² = 4 — scrivo 4 e non riporto niente: 4
• 2·4·2 = 16 — scrivo 6 e riporto 1: 64
• 4² = 16, aggiungo il riporto: 16+1 = 17 — scrivo 17: 1764

---

Come elevare al quadrato un numero che finisce per 5

Riprendendo quanto detto sopra, e notando che un numero che finisce per 5 può essere scritto come (10a + 5), con a eventualmente anche maggiore di 9, abbiamo che

(10a + 5)² = 100a² + 100a + 25 = 100a(a + 1) + 25

da cui si deduce che i quadrati di tutti i numeri che finiscono per 5 hanno, come ultime due cifre, 25; le cifre più a sinistra (quindi centinaia, migliaia, eccetera) si ottengono moltiplicando a per a + 1. Quindi il procedimento è:

• si prende il numero ottenuto cancellando la cifra delle unità del numero dato e lo si moltiplica per il successivo, si scrive il risultato
• alla destra del risultato si scrive 25

Esempio, vogliamo calcolare il quadrato di 65:

• cancello il 5, rimane 6 — lo moltiplico per il successivo, cioè 7, ottengo 6·7 = 42 
• scrivo 25 a destra di 42: 4225.

---

Come moltiplicare due numeri vicini tra loro.

Si può usare il prodotto notevole (a + b)(a − b) = a² − b² per calcolare il prodotto di due numeri p e q, se li si riesce a esprimere come somma e differenza di altri due numeri a e b (se sono vicini, la differenza a − b è un numero piccolo, e i calcoli risultano piu facili)

Esempio: calcolare il prodotto 41·43.

Si esprime 43 come 42 + 1 e 41 come 42 − 1, e quindi si calcola (42 + 1)(42 − 1) = 42² − 1² (il quadrato di 42 può essere calcolato con il metodo indicato sopra) =
1763.

---

Come moltiplicare per 11

Il prodotto di un qualunque numero a per 11 può essere calcolato seguendo questo procedimento:

• si scrive la prima cifra
• si sommando le cifre consecutive di a a 2 a 2, tenendo conto dei riporti
• si scrive l'ultima cifra.

Esempio: calcolare 1489·11.

• si scrive la prima cifra: 1
• Si sommano le cifre a 2 a 2 (le scrivo separate da parentesi, che non indicano prodotti): 1(1+4)(4+8)(8+9)
• Si scrive l'ultima cifra: 1(1+4)(4+8)(8+9)9
• Si eseguono i calcoli tra parentesi: 1(5)(12)(17)9
• Andando da destra a sinistra, si scrive una sola cifra per raggruppamento e si tiene conto dei riporti: 1(5+1)(2+1)(7)9 = 16379

---

(Questo post si aggiornerà se verranno suggeriti altri trucchi strabilianti (e se mi ricorderò di farlo)).

Allora, questi angoli retti sono congruenti o no?

“Ma allora com'era la soluzione del paradosso degli angoli retti diversi?”.

“Hai provato a studiare il problema?”.

“Eh, sì, però non ho mica capito quale fosse l'errore: i due triangoli coi lati rosso, verde e viola sono effettivamente congruenti”.

“E questo è giusto”.

“Ma allora? Non è possibile!”.

“L'errore, questa volta, sta nella figura”.

“Ma come? La figura è corretta, non capisco”.

“La figura è sbagliata. Tu hai guardato quella che ho fatto io e non hai provato a costruirtela in autonomia, vero?”.

“Mah, a dir la verità ho provato a fare qualche scarabocchio, però non ho ottenuto nessun risultato. In fondo, che senso ha rifare una figura che ho già davanti?”.

“Se la figura è fatta bene potrei darti ragione, e però in questo caso non era fatta bene. Prova a farla utilizzando qualche strumento un po' preciso, senza pensare alla figura che già hai davanti”.

“Boh, proviamo pure”.

“Ti descrivo la procedura, poi tu esegui le varie operazioni, in questo modo non ti fai ingannare dalla figura che hai in mente”.

“OK”.

“Allora, disegna il rettangolo ABCD”.

“Fatto”.

“Ruota il segmento AB intorno al punto A, in senso orario, di un angolo scelto da te, a piacere. Il segmento ruotato lo puoi chiamare AE”.

“Bene”.

“Congiungi C con E, poi traccia gli assi dei due segmenti DA e CE. Chiama F il loro punto di intersezione”.

“Fatto. Oh”.




“Capisci, adesso?”.

“Capisco, i triangoli sono congruenti ma non sono disegnati come pensavo io. Ma forse se ruoto un po' di meno il primo segmento…”.

“Prova pure, questa non è un'immagine, puoi trascinare il punto E dove vuoi”.

“Uh. Ci deve essere una morale, in questa storia”.

“Già. Non fidarti dei disegni fatti dagli altri”.

“Pensavo a qualcosa un po' più zen”.

“Non fidarti, pensa”.

“OK”.

Scienziaggini

Mix, allonimo di Cristiano Micucci, non lo conoscevo mica prima di iniziare a frequentare l'ex socialino dell'odio (che dopo la chiusura è rinato e ogni giorno ha qualcosa di nuovo e tu lo guardi crescere come se fosse un bambino, poi ti rendi conto di stare per cadere nel ridicolo e allora smetti, ma non per molto).

Dicevo, Mix non lo conoscevo, e quando ho saputo che sarebbe uscito un suo elettrolibro per i tipi di 40k mi sono detto: ma pensa, non sapevo che fosse un matematico.

E infatti non lo è.

In realtà a Mix piace scrivere, e in questo libro lo fa parlando di cose di scienza, ma non come lo farebbe un Vero Scienziato. Lo fa in modo umoristico, che quando leggi ti sembra che sia una cosa seria e poi, zac, ti trovi in un altro universo in cui è possibile viaggiare nel tempo (ma solo in modalità base base), in cui abbiamo avuto un primo contatto con una specie extraterrestre, in cui la siepe di cui Leopardi parla nella sua L'infinito è… beh, oh, non posso mica dire tutto sennò spoilero troppo.

Bene, il titolo del libro è Scienziaggini, lo potete trovare su amazon o bookrepublic, costa 1.99 euro. Leggetelo, ha anche una prestigiosa prefazione scritta da un Vero Scienziato.

Non tutti gli angoli retti sono congruenti

A colori uguali corrispondono oggetti uguali. Dunque un angolo maggiore di un angolo retto è congruente a un angolo retto. Ehm.

---

Edit: siccome dal disegno non si capisce la costruzione, la esplicito qua, anche se non ho lettere sui vertici della figura.

Dato un rettangolo (quello coi lati blu e rossi in alto), ruotare di un certo angolo uno dei suoi lati (quello rosso in alto a destra). Costruire l'asse del lato lungo del rettangolo e l'asse del segmento arancione: si formano due triangoli isosceli (quello coi lati viola e quello coi lati verdi).

I due triangoli coi lati rosso, viola e verde risultano così congruenti.

Il determinante di una matrice, questo sconosciuto (per non parlare dei parallelotopi)

Qualcuno ricorderà, dalle scuole superiori, di avere già sentito nominare la parola determinante. Magari legata a un magico metodo per risolvere i sistemi di equazioni, il metodo di Cramer (che, tra parentesi, non si scrive con la K). Un metodo che aveva a che fare con le matrici, che sono poi griglie di punti — per la precisione, le matrici di cui si può calcolare il determinante sono griglie quadrate di punti.

Chi, all'università, studia matematica, o fisica, o qualche ingegneria, probabilmente incontra le matrici per la prima volta nel corso di geometria, l'unica materia che si studia senza fare nemmeno una figura (è così, sembra assurdo ma è così). La definizione di determinante di una matrice è del tutto incomprensibile: provo a scriverla in italiano.

Il determinante di una matrice quadrata n×n è dato dalla somma, fatta su tutte le permutazioni di n elementi, dei prodotti tra il segno della permutazione considerata e gli elementi di ogni riga (o di ogni colonna) riordinati secondo la permutazione stessa.

In formule:

La prima domanda che mi sono fatto io quando ho visto questa definizione è stata: ma come hanno fatto a pensarci? Quale mente malata può produrre una roba del genere? Nessuno te lo spiega, naturalmente, e tu rimani lì a bocca aperta in balia di sentimenti contrastanti: ammirazione per chi ha potuto pensare a una cosa del genere (che funziona, eh, non è scritta a caso) e odio per chi ha potuto pensare a una cosa del genere (che funziona, ma come è possibile che funzioni, santo cielo?).

Prima di provare a dare una spiegazione, ecco una citazione di un famoso matematico, Arnold, uno che faceva disegnini per ogni cosa (disegnava anche gattini) (per spiegare la matematica):

The determinant of a matrix is an (oriented) volume of the parallelepiped whose edges are its columns. If the students are told this secret (which is carefully hidden in the purified algebraic education), then the whole theory of determinants becomes a clear chapter of the theory of poly-linear forms. If determinants are defined otherwise, then any sensible person will forever hate all the determinants, Jacobians and the implicit function theorem.

Ecco. Visto cosa dice sul segreto indicibile riguardante il determinante?

Bene, proviamo allora a capire la definizione geometrica, quella con i disegnini. Partiamo da un parallelogramma:



Potete giocare un po' con l'applet trascinando le punte dei vettori: si vede bene che l'area dipende da quanto sono lunghi i vettori e dall'angolo compreso tra essi (se l'angolo diventa molto piccolo anche l'area diventa piccola). Se i due vettori sono sovrapposti (collineari, come dicono i Veri Matematici), l'area diventa nulla, e in effetti la figura non è più bidimensionale, ma è un segmento.

La stessa cosa vale in tre dimensioni e, se siete capaci di astrarre e diventare Veri Geometri, anche in un numero maggiore di dimensioni.



Il volume diventa uguale a zero quando almeno due dei tre vettori diventano collineari (se ci provate con la figurina qua sopra non è detto che ci riusciate, perché spostare con il mouse una proiezione bidimensionale di un oggetto tridimensionale non è facile. Insomma, il software fa quello che può (e che vuole)).

Ora, quello che vogliamo fare è definire un Coso Matematico che ci permetta di calcolare volumi di oggetti definiti come quelli qui sopra (cioè se parallelogrammi, con due vettori; se parallelepipedi, con tre vettori; se n-parallelotopi (pare che si chiamino così), con n vettori). Come fare?

Prima di tutto, la notazione: immaginiamo che i vettori partano tutti dall'origine, e quindi per definirli ci bastano le coordinate della loro punta. Due coordinate se siamo sul piano, tre coordinate se siamo nello spazio, n coordinate se siamo in spazi di dimensione n. Ecco, queste coordinate le mettiamo in colonna, formando una matrice (se decidessimo di metterle in riga non cambierebbe nulla, ma per fissare le idee pensiamo alle coordinate dei punti scritte in colonna).

Prima regola: un (iper)cubo di lato 1 deve avere area 1. In 2 dimensioni il cubo si chiama quadrato, definito dai vettori aventi estremi in (1,0) e (0,1), e quindi vogliamo definire il determinante in modo che dia come risultato 1 se applicato alla matrice avente come colonne (1,0) e (0,1). Insomma, in formule:

Questo deve valere in generale: in tre dimensioni, ad esempio, avremmo una matrice con tre righe e tre colonne così fatte: (1,0,0), (0,1,0), (0,0,1).

Insomma, abbiamo la

Regola 1: il determinante di una matrice avente 1 sulla diagonale che va dall'alto a sinistra al basso a destra e 0 in tutte le altre caselle deve valere 1. E fin qua ci siamo, andiamo avanti.

D'ora in poi indico con A₁, A₂, …, A_n le colonne della matrice (cioè le coordinate delle punte dei vettori).

Poco sopra abbiamo detto che se due vettori sono uguali allora il determinante deve dare zero. Quindi ecco la

Regola 2: det(A₁, …, A_i, …, A_j, …, A_n) = 0 se A_i = A_j per qualche coppia di valori i, j con i diverso da j.

Andiamo avanti: se moltiplichiamo un lato del parallelepipedo per un fattore λ (ai matematici che giocano con le matrici piace molto la lambda, chissà perché), allora il volume deve essere moltiplicato anch'esso per lo stesso valore. Quindi ecco la

Regola 3: det(λA₁, …, A_n) = λdet(A₁, …, A_n) — e questo deve valere per tutte le colonne della matrice, non solo per la prima.

Ora arriva una specie di proprietà distributiva. Cerchiamo di capirla prima con una figura (bidimensionale, così la vediamo meglio, eh):



Anche qua potete spostare le punte dei vettori. L'idea è questa: la somma delle aree dei due parallelogrammi azzurri è uguale a quella di quello rosso (i due triangoli che si formano sopra e sotto sono congruenti, in sostanza)(non fate commenti sui colori). Da qui deduciamo la

Regola 4: det(A₁ + B₁, …, A_n) = det(A₁, …, A_n) + det(B₁, …, A_n), e questo deve valere per tutte le colonne, non solo per la prima.

Ebbene, queste quattro regole ci permettono di definire il determinante e di arrivare alla Formulaccia Incomprensibile scritta lassù, basta fare un po' di giochini. Per esempio:

det(A₁ + A₂, A₁ + A₂, …, A_n) deve essere uguale a 0 per la regola 2 (ci sono due colonne uguali), ma se applichiamo per tre volte di seguito la regola 4 abbiamo che

det(A₁ + A₂, A₁ + A₂, …, A_n) =
= det(A₁, A₁ + A₂, …, A_n) + det(A₂, A₁ + A₂, …, A_n)
= det(A₁, A₁, …, A_n) + det(A₁, A₂, …, A_n) + det(A₂, A₁, …, A_n) + det(A₂, A₂, …, A_n)
= 0 + det(A₁, A₂, …, A_n) + det(A₂, A₁, …, A_n) + 0,

da cui ricaviamo che det(A₁, A₂, …, A_n) + det(A₂, A₁, …, A_n) = 0. Ed ecco la

Proprietà 1: scambiando di posto due colonne si inverte il segno del determinante (qui sono state scambiate le prime due, ma potete tranquillamente scambiare quelle che volete). E cambiare l'ordine di due vettori significa cambiare l'orientazione, ecco perché il determinante è il volume orientato del parallelepipedo. Insomma, diamo un significato anche al segno negativo.

Queste regole definiscono il determinante in modo non ambiguo, cioè lo caratterizzano. Vediamo per esempio come si fa per calcolare

Con la notazione usata qui (più comoda per un blog che usa l'html e non il LaTeX), i calcoli sono questi:

A = det((a,c), (b,d)) = det( a(1,0) + c(0,1), b(1,0) + d(0,1))

(applicando la regola 4:)
= det(a(1,0), b(1,0)) + det(a(1,0), d(0,1)) + det(c(0,1), b(1,0)) + det(c(0,1), d(0,1))

(applicando la regola 3;)
= ab[det((1,0), (1,0))] + ad[det((1,0), (0,1)] + bc[det((0,1), (1,0)] + cd[det((0,1), (0,1))]

(applicando la regola 2:)
= ab0 + ad[det((1,0), (0,1)] + bc[det((0,1), (1,0)] + cd0

(applicando la proprietà 1:)
= ad[det((1,0), (0,1)] − bc[det((1,0), (0,1)]
= (ad − bc)[det((1,0),(0,1)]

(applicando la regola 1:)
= ad − bc.

Ecco qua. Come si diceva a scuola: diagonale principale meno diagonale secondaria.

Se si applicano le stesse regole a matrici di ordine superiore ecco che salta fuori la somma fatta sulle permutazioni degli indici di cui si parlava all'inizio. Ora, almeno, c'è un perché che dà un'idea del motivo per cui la definizione sia fatta in quel modo.

Questo non è il percorso storico che ha portato alla definizione di determinante, e si può fare tanta matematica senza avere presente questo aspetto geometrico. Conoscerlo, però, secondo me è meglio.

---

Credits a Quora, che ogni tanto ha cose interessanti.

La ricetta definitiva dei tortellini

Mia suocera non era come le suocere delle barzellette: mi voleva bene e mi faceva sentire come uno di famiglia. Una volta ogni due settimane ci invitava a casa sua per il pranzo della domenica, e la scena tipica era questa: annunciava di aver preparato una certa ricetta, alla quale però aveva apportato alcune modifiche, perché magari non aveva in casa il tal ingrediente e allora lo aveva sostituito con un altro, perché una volta il piatto non era venuto bene e allora aveva aggiunto, tolto, modificato qualcosa, sentite un po' se è buono, non sarà troppo insipido, secondo me adesso è meglio. Cose così.

In pratica quando una ricetta entrava nella sua cucina veniva provata, modificata, migliorata, a volte stravolta, con un procedimento di approssimazioni successive che portava verso la perfezione.

Si chiamava Giuseppina, ma in realtà tutti l'hanno sempre chiamata Pina (potrei sottolineare quel tutti narrando la leggenda su mia moglie che pare abbia conosciuto il nome vero di sua mamma solo molto tardi (per molto tardi intendo verso i sedici anni) (ma è solo una leggenda, appunto, quindi non lo farò)); comunque da quando ha iniziato ad avere nipoti era nota come la nonna Pina — come quella della canzone, esatto, ma la canzone è venuta dopo.

La nonna Pina ora non c'è più, se n'è andata improvvisamente due settimane fa. I suoi figli il giorno della festa del papà erano soliti festeggiare, assieme a suo marito, anche il suo onomastico.

E io, oggi, la ricordo così, con il suo capolavoro culinario frutto di sperimentazioni e esperienza: i tortellini. Non so se esista una ricetta ufficiale, un qualche documento depositato, un marchio dop, igp, stg, boh. Non mi interessa: i migliori tortellini li ho mangiati a casa sua, e questo basta.

Dunque, ecco la sua ricetta, così come è stata raccolta da un'amica che è stata a casa sua a lezione di tortellini.

---

Prodotto finito: 130 g a testa (adulti)

RIPIENO per 2 kg finiti:

600 g polpa di maiale (prosciutto) a pezzi, sbollentata e poi tritata con:
1 hg di mortadella
1 hg di prosciutto crudo
2.5 hg parmigiano reggiano grattugiato
2 uova
noce moscata e sale (se serve)

BRODO: mezza gallina + 8 hg di manzo. Bollire per 2 ore circa. Segreto: mettere anche un dado. (Questo non me l'aveva mai detto, sapeva che io e il dado non andiamo molto d'accordo)

NB: Se i tortellini avanzano dopo il pasto, separarli dal brodo. Poi, la volta seguente, riscaldare solo il brodo.

---

Breaking news: un recente ritrovamento (bigliettino giallo scritto a matita), di datazione più recente rispetto alla ricetta riportata sopra, riporta un rapporto carne/mortadella/prosciutto pari a 4/1/1 e non 6/1/1. Provate e guardate un po' cosa vi piace di più.

---

Per quanto riguarda il ripieno: la procedura di sbollentare la polpa e poi tritarla è stata sostituita dalla seguente. Si trita la polpa di maiale, la si cuoce in pentola, la si trita nuovamente assieme al prosciutto crudo e alla mortadella.

Polinomi e dadi

“Mi hanno proposto un quesito che mi sembrava facile, e invece…”.

“Eh, succede spesso con le cose che sembrano facili. Uno dice dai, è semplice, si farà così e cosà, poi quando prova a risolvere si pianta”.

“Già”.

“Ma il quesito in questione qual è?”.

“Questo: abbiamo dei dadi a sei facce numerate in un modo non standard, cioè con i numeri 0, 0, 1, 2, 3, 4. Ne lanciamo cinque e sommiamo le cifre che vediamo: quali sono le probabilità di ottenere i numeri da 0 a 20?”.

“Hai ragione, non è per niente facile. Esiste un metodo per provare a risolvere quesiti del genere, metodo che fornisce una soluzione semplice da scrivere ma comunque difficile da calcolare”.

“Andiamo bene”.

“Eh, lo so, alcuni problemi sono proprio difficili, non si riescono a trovare (o non esistono, chissà) formule semplici per risolverli.”.

“Ma quindi questo si risolve o no?”.

“In un certo senso, sì”.

“Uhm”.

“Ma il bello non è tanto il risultato, quanto la strada percorsa per arrivarci”.

“Ti sento molto zen”.

“Quando la strada ti permette di vedere un problema da tanti punti di vista che apparentemente sembrano scollegati uno dall'altro, nel momento in cui scopri un filo conduttore che li lega tutti quanti ecco che ti sembra di raggiungere l'illuminazione”.

“Sempre più zen”.

“Provo a spiegarti il metodo, ok?”.

“Vai”.

“Partiamo da un caso semplice, però”.

“Mi sembra giusto”.

“Prendiamo un dado a due facce…”.

“Una moneta, insomma”.

“Sì, ma numeriamo le facce con i due numeri 0 e 1, poi lanciamo un po' di monete e cerchiamo di calcolare quello che succede”.

“Va bene”.

“Con una moneta è facile, puoi ottenere solo 0 e 1”.

“E vabbé”.

“Con due monete puoi ottenere i valori 0, 1 e 2”.

“Ma non con la stessa probabilità, no?”.

“Esattamente. Facciamo uno schema di quello che può succedere:”.

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 2

“È più facile ottenere 1 che non 0 oppure 2”.

“Certo. Se riportiamo questo problema al tuo problema, hai solo molti più conti da fare, ma compilando uno schema come questo ce la fai sempre”.

“Grazie! Ma uno schema come questo è lunghissimo da fare. Ho provato, sai? Ma poi ho lasciato lì in fretta, i valori intermedi tra 0 e 20 si possono ottenere in un'infinità di modi diversi, ci si perde”.

“Perfetto, questo è esattamente il problema: troppi conti da fare senza nessuna regola semplice che ci permetta di evitarli”.

“Eh, e quindi?”.

“Quindi adesso cambio completamente problema, te ne propongo un altro che non ha niente a che fare con questo, e poi scopriremo invece che non è così”.

“Sono curioso, sentiamo”.

“Sai calcolare il quadrato di un binomio?”.

“Uh, ma cosa c'entra… ok, ok, come non detto. Sì, se mi ricordo bene, sì: quadrato del primo più doppio prodotto del primo per il secondo più quadrato del secondo”.

“Ricordi bene. Sai applicarlo a questo binomio?”.

(1 + x)²

“Direi proprio di sì, viene 1 + 2x + x²”.

“Ok. Ora, dimmi, perché si fa il doppio prodotto?”.

“Eh, uh, perché… perché sì!”.

“…”.

“Ok, ora non ricordo bene, ehm. Ma, boh, probabilmente uno ha provato una volta a fare la moltiplicazione e si sarà accorto che va bene così”.

“Vuoi provare tu?”.

“A calcolare il quadrato come se fosse (1 + x)(1 + x)?”.

“Sì”.

“Ah, va bene, allora: 1 + x + x + x². I due termini di primo grado si sommano e risulta quello che avevo detto”.

“Bene. Come potresti spiegare il motivo per cui risultano due termini di primo grado che si sommano e uno solo di secondo grado?”.

“Beh, i due termini di primo grado sarebbero uno 1·x, l'altro x·1. Insomma, una volta moltiplico l'uno che si trova nella prima parentesi con la x che si trova nella seconda, l'altra invece moltiplico la x che si trova nella prima parentesi con l'uno che si trova nella seconda”.

“E il termine di secondo grado, invece?”.

“Per quello è ancora più semplice: c'è un solo modo di ottenerlo”.

“Quale?”.

“Moltiplicare la x della prima parentesi con la x della seconda”.

“Quindi, riassumendo: nel risultato hai tre termini, uno di grado 2, uno di grado 1, e un termine noto che è di grado 0”.

“Giusto”.

“Il termine di grado 0 lo puoi ottenere soltanto moltiplicando due termini di grado 0”.

“Certo”.

“In simboli: 0 + 0 = 0”.

“Già”.

“Il termine di grado 2 lo puoi ottenere in un solo modo, moltiplicando due termini di grado 1”.

“Vero anche questo”.

“In simboli: 1 + 1 = 2”.

“Uh, ma questa è la tabella che hai fatto prima coi possibili risultati dei dadi!”.

“Già: concludi tu”.

“Il termine di grado 1 lo posso ottenere in due modi, moltiplicando un termine di grado 0 per uno di grado 1, oppure viceversa, moltiplicando un termine di grado 1 per uno di grado 0. In simboli: 0 + 1 = 1 e anche 1 + 0 = 0”.

“Ecco il filo conduttore: nel lancio di due dadi con i numeri 0 e 1 sulle facce e nel calcolo dello sviluppo del quadrato di (1 + x) si fanno gli stessi calcoli”.

“Roba da matti”.

“Proviamo a farlo con tre dadi?”.

“Sempre con due facce?”.

“Per adesso sì. Facciamo prima una tabellina coi risultati possibili, con tre dadi ci si riesce ancora”.

“Faccio subito, dovrebbe essere questa:”.

0 + 0 + 0 = 0

1 + 0 + 0 = 1
0 + 1 + 0 = 1
0 + 0 + 1 = 1

1 + 1 + 0 = 2
1 + 0 + 1 = 2
0 + 1 + 1 = 2

1 + 1 + 1 = 3

“Bene, quindi hai un modo per fare 0, tre modi per fare 1 oppure 2, e un modo per fare 3”.

“Ok. E il quadrato di binomio?”.

“Questo non sarà più un quadrato, perché puoi anche ottenere 3 come risultato. Prima hai calcolato il quadrato perché il risultato più alto che potevi ottenere lanciando due dadi era 2, e analogamente il grado più alto che puoi ottenere facendo il quadrato di (1 + x) è 2”.

“Adesso quindi devo fare il cubo, dato che ho un massimo uguale a 3?”.

“Esatto”.

“Vediamo, ehm, non ricordo bene, mumble mumble, uno più x al quadrato, poi ancora per uno più x, puff pant…”.

“Tutto bene?”.

“Ehh, sì, ecco, due più uno, fatto! Mi viene così: 1 + 3x + 3x² + x³”.

“Perfetto. Hai capito la corrispondenza tra questo polinomio e la tabella che abbiamo fatto prima?”.

“Sì, sì! Molto bella! Quell'uno che ho trovato corrisponde all'unico modo che ho di ottenere 0”.

“E osserva che 0 è proprio il grado del monomio 1”.

“Giusto. Invece 3x corrisponde ai 3 modi di ottenere 1. In effetti 3x è 3x¹, il grado della x corrisponde al risultato”.

“Molto bene. Poi hai visto che hai altri tre modi di ottenere 2”.

“E questo fatto si traduce nella presenza del monomio 3x². Alla fine poi ho un solo modo di ottenere 3, e infatti nello sviluppo del cubo di binomio ho proprio un solo termine x³”.

“Perfetto. Ora generalizziamo in un'altra direzione”.

“In che senso?”.

“Abbiamo due dadi, questa volta con tre facce”.

“E come sono fatti?”.

“Beh, non importa, fai finta che esistano. Nella pratica puoi prendere un dado a sei facce e numerate 0, 0, 1, 1, 2, 2, ma non complichiamo le cose, vorrei ragionare proprio su tre sole facce”.

“Ah, va bene. Numerate da 0 a 2, allora?”.

“Esatto. Fai la tabellina dei possibili risultati?”.

“Pronti.”.

0 + 0 = 0

1 + 0 = 1
0 + 1 = 1

2 + 0 = 2
1 + 1 = 2
0 + 2 = 2

2 + 1 = 3
1 + 2 = 3

2 + 2 = 4

“Ora pensiamo a come costruire il polinomio che corrisponde a questo dado”.

“Uhm, tre facce, come si fa?”.

“Pensa a dove memorizzavi, nel caso precedente, i valori scritti sulle facce”.

“Erano gli esponenti della x, i gradi dei singoli monomi, insomma”.

“Ora hai tre facce…”.

“E quindi tre valori, allora devo scrivere un trinomio questa volta?”.

“Esatto”.

“Va bene (1 + x + x²)?”.

“Va benissimo, è lui. Il numero di lanci, invece, dove lo utilizzavi?”.

“Era l'esponente del polinomio. Quindi adesso dovrei calcolarmi (1 + x + x²)²?”.

“Già”.

“Eh, ehm, devo farlo a mano?”.

“Permettimi di ricordarti la formula, così facciamo prima”.

“Ne hai facoltà”.

“Devi calcolarti tre quadrati e poi aggiungere i tre possibili doppi prodotti”.

“Ah. Allora faccio i conti”.

(1 + x + x²)² = 1 + x² + x⁴ + 2x + 2x² + 2x³.

“Bene, ma non hai finito, metti insieme i termini simili”.

“Ah, già. Ecco:”.

(1 + x + x²)² = 1 + 2x + 3x² + 2x³ + x⁴.

“E, come vedi, i conti tornano, il risultato corrisponde alla tabella di prima”.

“Devo dire che questa connessione tra dadi e polinomi è affascinante. Quindi potrei risolvere in questo modo anche il mio problema originale?”.

“Esatto. Ma, per fare un'analisi completa, lasciami fare prima un'altra domanda: cosa succederebbe se le facce del nostro dado non avessero la stessa probabilità di uscire?”.

“Uh?”.

“Supponi che il dado a due facce non sia equilibrato, ma che 2 volte su 3 esca lo zero, mentre 1 volta su 3 esca l'uno. Come facciamo l'analisi?”.

“Boh?”.

“Fai una tabella…”.

“Eh, ma con probabilità diverse come si fa?”.

“Fai finta che il dado abbia tre facce”.

“Ah! Un dado con le facce numerate così: 0, 0, 1”.

“Già. Prova a lanciarlo due volte”.

“Ok, ecco la tabella:”.

0 + 0 = 0

1 + 0 = 1
0 + 1 = 1

1 + 1 = 2

“Siamo sicuri?”.

“Eh, in effetti mi viene uguale a quella del dado a due facce. Come faccio a tener conto del fatto che ci sono due facce uguali?”.

“Fai finta, inizialmente, che siano diverse. Invece di numerarle con 0, 0, 1 usa un'altra simbologia, in modo da distinguere i due zeri”.

“Ah, allora numero i due zeri in modo diverso, li chiamo 0₁ e 0₂. Ecco quello che potrei ottenere”.

0₁ + 0₁ = 0
0₁ + 0₂ = 0
0₂ + 0₁ = 0
0₂ + 0₂ = 0

0₁ + 1 = 1
0₂ + 1 = 1
1 + 0₁ = 1
1 + 0₂ = 1

1 + 1 = 2

“Ok, quindi hai quattro modi per fare 0, quattro modi per fare 1 e un solo modo per fare 2”.

“E coi polinomi come faccio?”.

“Prova a calcolare il quadrato di (2 + x)”.

“Ah! Risulta 4 + 4x + x²”.

“Come vedi, tutto torna”.

“Ma quindi uso (2 + x) invece di (1 + x) perché ci sono due facce uguali?”.

“Puoi ragionare in due modi diversi. Il primo è questo: usi 2 al posto di 1 perché hai 2 casi in cui esce il numero 0, e non uno solo. Altrimenti puoi sempre immaginare di avere una faccia in più, e quindi in realtà quello che stai calcolando è il quadrato del trinomio (1 + 1 + x) ”.

“Perfetto”.

“In sostanza, i coefficienti delle incognite nel polinomio sono legati alla probabilità di uscita della corrispondente faccia del dado”.

“Mentre il valore presente sulla faccia corrisponde all'esponente dell'incognita in ogni monomio”.

“È così. Tutto si basa sulla regola che trasforma la moltiplicazione di potenze con la stessa base in una somma di esponenti”.

“E questa è la somma dei valori delle facce”.

“Sì, mentre la probabilità di uscita di ogni faccia può essere vista come un peso assegnato al valore corrispondente: nel nostro esempio lo zero pesa più dell'uno, perché ha più probabilità di uscita”.

“E allora di zeri ce ne mettiamo due”.

“Già. Volendo potresti mettere come coefficiente della x proprio la probabilità di uscita di quella faccia, in questo caso avresti a che fare con coefficienti frazionari, ma siccome essi avrebbero tutti lo stesso denominatore, potresti raccoglierlo a fattor comune e portarlo fuori dalla parentesi”.

“In sostanza farei gli stessi calcoli”.

“Sì, si tratta di vedere se preferisci lasciare sottinteso il denominatore, o se invece vuoi esplicitarlo: non cambia niente. E ora sei pronto a risolvere il problema del tuo dado”.

“Provo, eh. Allora, sei facce, quindi devo costruire un… esanomio?”.

“Facciamo un polinomio di sei termini”.

“Forse è meglio, sì. Le facce hanno valore 0, 0, 1, 2, 3, 4: questi sono gli esponenti dell'incognita”.

“E sono anche tutte equiprobabili”.

“Giusto, quindi i coefficienti sono uguali a 1. Il polinomio dovrebbe essere questo: (1 + 1 + x + x² + x³ + x⁴)”.

“E siccome lanci il dado cinque volte…”.

“Devo elevare il polinomio alla quinta. Ecco la formula finale:”.

(1 + 1 + x + x² + x³ + x⁴)⁵

“Bene”.

“Sì, ma, ehm, quanto fa?”.

“Ah, boh, bisogna farsi tutti i calcoli. Ricordi che all'inizio di questo discorso avevamo detto che il quesito si risolve in un certo senso?”.

“Eh”.

“Beh, in teoria è risolto, devi solo metterti lì a fare i conti. Rispetto a farsi tutta la tabella con tutte le possibili combinazioni dei risultati è comunque un passo avanti”.

“Questo è vero, però è una soluzione deludente”.

“Non si può fare di meglio, i calcoli sono proprio brutti. Un punto chiave del problema è capire in quanti modi puoi ottenere un numero, per esempio 8, sommando cinque valori presi dall'insieme che contiene 0, 1, 2, 3, 4”.

“È proprio quello il problema, avevo cominciato a fare i conti ma sono tantissimi”.

“Già: sono 905”.

“Cosa? Così tanti? E come hai fatto a calcolarlo?”.

“Beh, oggi certi calcoli possiamo farli fare alle macchine. Ecco qua lo sviluppo del tuo polinomio elevato alla quinta:”.

x²⁰ + 5x¹⁹ + 15x¹⁸ + 35x¹⁷ + 75x¹⁶ + 141x¹⁵ + 235x¹⁴ + 355x¹³ + 505x¹² + 655x¹¹ + 781x¹⁰ + 865x⁹ + 905x⁸ + 855x⁷ + 745x⁶ + 601x⁵ + 450x⁴ + 280x³ + 160x² + 80x + 32.

“Santo cielo”.

“Pensa a quando questi conti si facevano tutti a mano”.

“Mo'c lavòr”.

---

[EDIT: ho dimenticato di inserire i ringraziamenti a chi ha partecipato alla risoluzione del problema. La discussione è iniziata sul socialino dell'amore, raggiungibile (finché dura) a questo link]