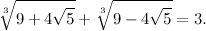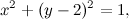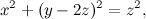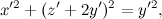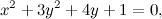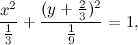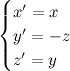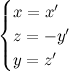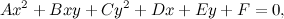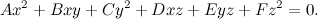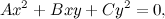Our whole universe was in a hot dense state

Le (più di cento) immagini che compongo la sigla iniziale di The Big Bang Theory.

Criteri di divisibilità (quasi) senza parole

Un numero è divisibile per 2 se la sua ultima cifra è divisibile per 2. E fin qua.

Complichiamo le cose con un disegnino. Scriviamo uno 0 e un 1, mettiamo un dito sullo 0, e cominciamo a contare da 0 al numero di cui vogliamo stabilire la divisibilità per 2, spostando il dito alternativamente sullo 0 e sull'1 che abbiamo scritto. Se finiamo la conta sullo 0, il numero è divisibile per 2, altrimenti non lo è.

Possiamo fare la stessa cosa per quanto riguarda la divisibilità per ogni numero: se vogliamo vedere se un numero è divisibile per 3, ad esempio, dobbiamo scrivere i numeri 0, 1 e 2 e contare, come se essi fossero collegati in maniera circolare, così:

Però, se il numero che stiamo studiando è molto grande, la faccenda diventa noiosa. Prendiamo un numero a caso, ad esempio 42. Se non vogliamo fare il giro dell'oca per 42 volte, possiamo scomporlo in decine e unità. Abbiamo 4 decine: dato che 3 decine sono certamente divisibili per 3, è come se avessimo una sola decina da considerare. E sappiamo che 10 è uguale a 9+1, quindi dopo aver contato per 40 passi dobbiamo finire sul numero 1. Poi aggiungiamo le 2 unità e arriviamo sullo 0: 42 è divisibile per 3. Bella forza.

La morale della storia è che invece di contare 42 volte si potrebbe contare solo 4 volte per le decine, 2 volte per le unità, e si ottiene il risultato corretto: il passaggio da decine a unità è come se non ci fosse. Ma perché succede questo? Funziona sempre così?

Proviamo ad analizzare quello che succede. Una decina, abbiamo detto, è uguale a 9+1, quindi fare 10 passi corrisponde a farne uno solo. Contare dunque le decine o le unità è la stessa cosa. Possiamo passare da decine a unità come se niente fosse, o anche da centinaia a decine, o da migliaia a centinaia, eccetera.

Vediamo che succede con 2 decine: dato che 20 è uguale a 18+2, contare 2 decine oppure contare 2 unità è uguale. Stessa cosa con 30: 30 è multiplo di 10 e quindi contare per 30 passi è come stare fermi sullo zero.

Potremmo allora generalizzare il nostro schema in questo modo: mettiamo il dito sullo 0, consideriamo la prima cifra del numero dato e cominciamo a contare. Ogni volta che cambiamo cifra (passando da decine a unità, o a centinaia a decine, o da migliaia a centinaia, eccetera) dobbiamo seguire una freccia rossa.

Ok, direte, è una cosa un po' inutile. È vero.

Proviamo a fare lo schema per il criterio di divisibilità per 4.

Qui le cose cambiano un po': 10, ad esempio, è uguale a 8+2, quindi se passiamo da una decina alle unità, dobbiamo saltare da 1 a 2. Invece 20 è un multiplo di 4, quindi quando passiamo da 2 decine alle unità, ripartiamo da 0. Infine, 30 è uguale a 28+2, quindi passando da 3 decine alle unità ripartiamo da 2.

La regola dunque è questa: conto sulle cifre nere, quando cambio posizione seguo una freccia rossa, poi ricomincio.

Ecco la divisibilità per 5 (questo è facile, le decine sono tutte divisibili per 5).

Il grafo per il criterio di divisibilità per 6 comincia a diventare interessante:

Ora arriviamo a un bel numero primo: 7

Tra l'altro, esiste un criterio di divisibilità per 7, ma è un po' complicato. Funziona in questo modo: dal numero dato si cancella l'ultima cifra e si sottrae dal risultato il doppio della cifra appena cancellata, e si va avanti così fino a che non si capisce se il numero ottenuto è multiplo di sette oppure no.

In formule:

x → x div 10 - 2(x mod 10)

Esempio: partiamo da 325 → 32 - 2×5 = 22, non divisibile per 7.
Altro esempio: partiamo da 294 → 29 - 2×4 = 21, divisibile per 7.

Esercizio: riuscite a dimostrare che il grafo della divisibilità per 7 è planare (cioè sta sul piano senza che vi siano intersezioni tra le varie frecce)? Qui la soluzione.

Dicono poi che il grafo per la divisibilità per 8 non sia planare, ma non conosco la dimostrazione. Comunque eccolo qua:

Ecco il 9:

(la prova del 9 ce la ricordiamo, no?).

Infine (saltando il grafo per il 10), ecco quello per la divisibilità per 11:

La disposizione dei numeri in queste figure è stata fatta da un programma, graphviz — io ho soltanto dovuto scrivere i vari collegamenti, ci ha pensato lui a dare una forma circolare al tutto. Se trovate dei modi migliori per rappresentare i vari criteri, fatemi sapere.

Ah, dimenticavo un ultimo grafo:

Non era una bugia

Quando, più di due mesi fa, ho parlato di Scienza Express, avevo detto che non ci avrei guadagnato niente nel farlo. Ed era proprio così. L'ho fatto perché si parlava di libri scientifici, perché mi piaceva l'idea di libri disponibili nel tempo, perché c'era un occhio di riguardo per gli insegnanti.

Poi mi sono detto: ehi, ma anche io sono un insegnante. E, ora che ci penso, anche io ho scritto una specie di libro, che è stato pubblicato su questo blog, che parlava di scienza (di matematica, per la precisione).

Allora ho riscritto ai due signori di Scienza Express e ho domandato: ma lo sapete che anche io ho scritto delle cose che forse vi possono piacere? Non è che magari vi interessano?

Bè, mi han detto sì.

Battlestar Galactica space and timeline

Se, durante la visione di Battlestar Galactica (e magari di Caprica) vi siete un po' persi, e ancora vi chiedete quante volte sono stati creati i cyloni, ecco una meravigliosa space and timeline.

(cliccare per ingrandire)

Poi dicono che la fisica è utile

In un tavolo da biliardo perfettamente piano le palle rotolano al centro.

Cose inutili

Wow

(Potevan fare in due parti tutti i film della serie, 'sti disgraziati)

Un'altra dimostrazione senza parole

Le meraviglie della termodinamica

Thermodynamics is a funny subject. The first time you go through it, you don't understand it at all. The second time you go through it, you think you understand it, except for one or two small points. The third time you go through it, you know you don't understand it, but by that time you are so used to it, it doesn't bother you any more.

Arnold Johannes Sommerfeld

(Visto su facebook)

Neal Stephenson — Anathem

Versione breve: leggetelo, è bellissimo.





Versione lunga: per prima cosa, non leggete i commenti in seconda e in quarta di copertina, sono pieni di spoiler.

Detto questo, provo a spiegare che cosa sia questo romanzo, senza rivelare niente. È stato diviso in due volumi per comodità della casa editrice, suppongo, ma l'originale è uscito in un volume unico. La copertina della versione inglese mostra il profilo di quello che sembra essere un monaco nell'atto di salire una scala, ma il nerd che è in noi non può fare a meno di notare l'analemma che è sovrapposto al nome dell'autore.



Le due copertine della versione italiana non sono, invece, molto significative. Vabbè, ringraziamo la Rizzoli comunque per aver tradotto quest'opera, anche se non potrà mai essere perdonata per non aver tradotto il terzo volume del Ciclo Barocco.

Neal Stephenson è un genio: riesce a scrivere opere coinvolgenti e per niente banali, in cui mescola stili diversi che rendono difficile la classificazione dei suoi romanzi. Questo, per esempio, in una prima approssimazione potremmo definirlo di fantascienza.

Quello che sto per dire viene spiegato nella prefazione, scritta dall'autore, o nelle prime pagine del libro, quindi potete leggere tranquillamente.

In un mondo che assomiglia alla terra, ma che non è la terra, scienza e tecnologia sono tenute il più possibile separate. Gli uomini di scienza, i pensatori, gli studiosi (chiamati avout nella lingua di quel mondo) vivono in strutture che assomigliano a monasteri: sono circondati da mura, sono separati dal mondo esterno, e non hanno comunicazione con esso. Sono perlopiù autosufficienti anche se, in qualche raro caso, è necessaria la consulenza o l'opera di qualche esperto esterno. Questi monasteri si chiamano mat (in originale, math). Il mondo matico è separato dal mondo esterno nel senso che nessuno, di regola, può attraversare le mura e andare nell'altro mondo. Esistono però gradi di separazione diversi: il gruppo degli unariani, per esempio, vive in mat i cui cancelli vengono aperti una volta all'anno, per dieci giorni. Durante quella specie di capodanno gli avout possono uscire e visitare il mondo esterno, e analogamente gli esterni (detti extramuros) possono visitare il mat. I decenariani, invece, aprono le loro porte solo ogni dieci anni. I centenariani addirittura ogni cento anni, per non parlare dei mitici millenariani che, finora, hanno aperto le loro porte solo tre volte.

Una piccola parentesi sulla lingua: dice l'autore che i neologismi che si trovano nel libro sono delle specie di traduzioni dalla lingua originale del mondo in cui è ambientata la storia all'inglese (e, per noi, dall'inglese all'italiano). Sono parole che sono state create in modo da dare al lettore delle suggestioni, delle sensazioni.

Per esempio, l'insieme dei giganteschi edifici (mat) che accolgono i vari avout, suddivisi per gruppi (unariani, decenariani, eccetera) si chiama concento. Ci ho messo una cinquantina di pagine per cogliere la doppia analogia con convento e con concentramento. In effetti questa faccenda dei neologismi all'inizio mi ha dato un po' fastidio, temevo che avrei subito dimenticato il significato e che non avrei capito niente nella lettura. Non è così, invece: dopo un po' ci si immerge nel mondo e sembra di essere a casa propria.

Bene, questo è l'inizio. Non vado avanti ulteriormente per non rivelare nulla della trama. Però posso ugualmente provare a spiegare perché questo libro mi è piaciuto.

Per esempio, è un libro sul platonismo.

Vi è piaciuto Godel, Escher, Bach. Un'eterna ghirlanda brillante, di Hofstadter? Siete rimasti affascinati dalle tecniche tipografiche/sintattiche di elaborazione dei teoremi dell'aritmetica? Del fatto che le cose funzionino anche senza la necessità che le stringhe dell'aritmetica abbiano un significato reale? Vi siete magari detti che non è vero, che quelle cose lì un significato ce l'hanno? Vi siete spinti, addirittura, a pensare che gli oggetti matematici possano avere un'esistenza reale?

Magari avete letto anche La mente nuova dell'imperatore, di Roger Penrose, il quale la pensa in modo oserei dire opposto rispetto a Hofstadter? E che suggerisce il fatto che la nostra coscienza sia legata alle strane proprietà che ci vengono raccontate dalla meccanica quantistica?

E, a proposito di meccanica quantistica, come vi ponete rispetto all'interpretazione a molti mondi?

Stephenson riesce ad inserire tutte queste cose in un romanzo che, comunque, rimane di fantascienza. Con, in alcuni momenti, un po' di sapore steampunk.

A poco a poco si capirà perché, in passato, è stato necessario separare il mondo matico da quello prassico (cioè gli scienziati dai tecnici), e si esploreranno le conseguenze di questo fatto. E basta così, non voglio raccontare di più.

Leggetelo, che è bello.

Gravity

Uno si mette davanti allo schermo nero, crea dei mondi, delle stelle, dei corpi celesti qualsiasi, e guarda cosa succede. Questo è Gravity.


(via smoot)

Il Cieco del Non-Spazio

Questo mese Urania Collezione propone un ottimo romanzo di Bob Shaw, Il Cieco del Non-Spazio. Dategli un'occhiata, se non lo conoscete.

Nei suoi romanzi, Bob Shaw inserisce sempre oggetti inventati da lui che poi saranno importanti nello sviluppo della trama. In questo romanzo sono i quasiocchi, che permetteranno al protagonista di…

Gnuovità

GnuGnu ha modificato la sua dimostrazione senza parole relativa ai formati An, producendo infine questa immagine.

Essenziale e chiara.

Sogni

C'è una frase alla quale ogni tanto penso quando ho bisogno di camminare con piede più leggero in questa valle di lacrime (ehm), una frase pronunciata da uno dei miei figli quando aveva quattro anni, che mi dà una sensazione di pace e di serenità di cui, a volte, ho bisogno, come ad esempio quando la cifra delle unità dei miei anni fa uno scatto in avanti e diventa uguale a quella delle decine. Bè, per non farla troppo lunga, la frase è questa:

Babbo, ma quando noi facciamo i sogni rimaniamo a casa?

Dimostrazione senza parole: ancora sui formati An

GnuGnu, che molti extramuros non conoscono perché è un avout centenariano del quale si sa poco, ha proposto un'altra dimostrazione senza parole relativa ai formati An della carta. Eccola qua:

Mi piace perché ci vedo il rettangolino rosso in movimento.

[Non sono impazzito, le parole strane derivano dalla mia attuale lettura, l'ultimo di Neal Stephenson (la descrizione del libro riportata su Anobii è uno spoiler dietro l'altro, non leggetela — appena finirò il libro mi premurerò di farne un elogio senza spoiler)]

Dimostrazione senza parole: i formati An

Prima di produrre la versione finale della sua dimostrazione senza parole relativa ai formati per la carta usati da noi europei, .mau. ha proposto un'altra versione della stessa dimostrazione, che non lo soddisfaceva molto. Io l'ho leggermente modificata e ve la propongo qua sotto, anche se non mi pare definitiva.

Insomma, non basta guardarla per comprendere la necessità del rapporto uno su radice di due nei formati An. Però è carina…

Hanno lanciato di nuovo un Saturn V

z ← z2+c

Per commemorare Benoit Mandelbrot, morto il 14 ottobre 2010, Scientific American ha ripubblicato un articolo pubblicato in origine nell'agosto del 1985 intitolato Computer Recreations: A computer microscope zooms in for a look at the most complex object in mathematics. Scritto dal buon Dewdney.

Si può scaricare il pdf direttamente da qui.

Cosa sia l'insieme di Mandelbrot lo sapete tutti, ma quell'articolo parla anche di una variante molto carina: prendiamo un numero intero compreso tra 0 e 99, eleviamolo al quadrato e teniamo solo le ultime due cifre del risultato. Poi ripetiamo il calcolo.

Bene, è chiaro che dopo (al massimo) 100 iterazioni dobbiamo avere una ripetizione, entrando in un ciclo. Quanti cicli ci sono? Che struttura hanno? Esistono degli attrattori? Avete provato a disegnare in un qualche modo i cicli? Avete notato delle simmetrie? Avete voglia (chiede Dewdney) di esplorare altri insiemi finiti (come, per esempio, gli interi da 0 a 999, elevandoli al quadrato ed estraendo le ultime tre cifre)?

Non bisogna dimenticare che l'articolo è stato scritto nel 1985, quando i personal computer non erano diffusi come lo sono oggi (ma la gente che li aveva sapeva programmarli). Dewdney suggerisce anche un algoritmo, avente lo scopo di ricercare eventuali cicli, che occupa solo due locazioni di memoria; così può essere eseguito anche dalle più semplici calcolatrici programmabili.

Altro che gigahertz e gigabyte.

Serendipità

Due ragazzi che abitano qua sotto hanno da poco aperto una gastronomia nel centro di Modena. Questa sera siamo usciti tutti quanti per andare a mangiare da loro, dato che era la serata utòber fest (ovvero Oktober Fest in dialetto modenese). Dopo la cena abbiamo approfittato della serata per fare un giretto in centro; in piazza Grande, di fianco al duomo, un gruppo di astrofili aveva installato un galileoscopio e quattro telescopi moderni: oggi e domani si celebrano le Galilean Nights 2010. Ho visto la luna da vicino, da ancora più vicino, Giove e quattro suoi satelliti.

(Se vi dicono che la luna non è fatta di formaggio, non credeteci)

Cose che voi umani

Il sottile confine che separa lo studente delle medie ancora bambino, vestito in modo normale, da quello che deve ogni giorno combattere contro impietosi attacchi ormonali, e che si veste mettendo in mostra le mutande e le forme di ciò che esse ricoprono, sta in una simpatica attività ideata dagli appartenenti al primo gruppo: attività che consiste nell'afferrare con due mani le mutande del compagno e tirare con forza verso l'alto.

Tale azione prende il nome di sparticulo.

Scienza Express

Non ho mai fatto pubblicità su questo blog. Primo, perché mi piace l'idea di essere libero di scrivere quello che desidero. Secondo, perché tanto non ci guadagno niente.

Oggi faccio un'eccezione. Primo, perché si parla di libri scientifici. Secondo, perché tanto non ci guadagno niente.

Insomma, ci sono questi due signori che hanno fondato una casa editrice che si chiama Scienza Express. Nel loro manifesto dicono che vogliono portare i libri a un clic e a pochi euro dai cittadini che non leggono ancora, dicono che vogliono rendere i libri disponibili nel tempo, e non lasciare che dopo pochi mesi siano già introvabili. E poi, udite udite, vogliono che gli insegnanti abbiano strumenti per lavorare e per pensare.

Insomma, dategli un'occhio: sono qua.

Dimostrazione senza parole

Prezi

Scopro oggi Prezi: trovo che queste presentazioni potrebbero essere una valida alternativa a quelle fatte in powerpoint usando il Comics Sans…

Sistemi di riferimento e relatività galileiana

Il PSSC ha prodotto, ormai troppi anni fa, una serie di filmati riguardanti i principali argomenti della fisica. Questo è uno dei più belli, date un'occhiata almeno all'inizio (peccato per quella pubblicità che compare proprio al centro del video).

Erlangen 1872 — Un modello per il piano proiettivo

Non è facile visualizzare il piano proiettivo. Facciamo fatica non solo perché i punti impropri sono all'infinito, e ci riesce difficile vedere fin là, ma anche a causa di una strana proprietà di cui godono questi benedetti punti.

La sostanza è questa: una retta possiede un solo punto improprio, ma va all'infinito seguendo due direzioni opposte. Detto in altri termini, due persone che si trovano su una retta e camminano verso l'infinito andando verso due direzioni opposte, arrivano allo stesso punto. È come se le rette possedessero una natura circolare.

Il disegno in prospettiva non ci aiuta nel visualizzare il piano proiettivo nella sua totalità: effettivamente ci permette di vedere la retta impropria, perché essa diventa la linea di orizzonte, ma questo non basta. Se la retta impropria è diventata propria, assumendo il ruolo di orizzonte, un'altra retta che prima era propria ha preso il suo posto. Insomma, una proiettività non può far diventare propria la retta impropria senza trovare un'altra retta che la sostituisca.

Se il piano proiettivo è formato dal piano euclideo usuale più la retta impropria, noi avremmo bisogno di qualcosa che comprima il tutto nella zona finita, e che non lasci nulla all'infinito. Un modello del piano proiettivo in cui tutto è visibile da occhi umani.

Bene, modelli di questo tipo esistono, ma sono molto strani.

Prima di tutto, abbiamo bisogno di una dimensione in più: per vedere il piano proiettivo abbiamo bisogno dello spazio normale (cioè euclideo). In secondo luogo, l'apparente natura circolare propria di ogni retta viene esplicitata utilizzando una sfera.

Siccome l'animazione aiuta molto di più di qualche disegnino, ecco un filmato che mostra come associare i punti di un piano a quelli di una sfera.



Le rette diventano cerchi massimi di una sfera (cioè circonferenze che stanno sulla sfera e hanno, come centro, il centro della sfera), e due cerchi massimi si incontrano sempre: anche se le corrispondenti rette sono parallele, essi si intersecano comunque, purtroppo in due punti. Dico purtroppo perché noi ne vorremmo uno solo, di punti di intersezione. Dato che invece ne abbiamo due (che sono sempre antipodali), dobbiamo compiere un'ulteriore operazione di astrazione: i punti antipodali sulla sfera devono essere identificati. Li dobbiamo immaginare come se fossero lo stesso punto: siamo ancora di fronte a quella apparente circolarità della retta di cui abbiamo parlato prima.

Se riusciamo a immaginare i punti antipodali come un solo punto, e i cerchi massimi come rette, siamo a posto: quello della sfera è un modello del piano proiettivo.

Altrimenti, se non ci piace il fatto di avere due punti che dobbiamo identificare mentalmente, possiamo costruire una figura in cui questi punti vengono effettivamente identificati.

Prendiamo la sfera e tagliamola a metà: in questo modo gettiamo via quasi tutti i punti doppi. Ci rimangono solo quelli del bordo, che devono essere identificati a due a due.

Cominciamo a prendere il bordo e a piegarlo, in modo da fare corrispondere ogni punto con quello diametralmente opposto.

E alla fine richiudiamo il tutto: purtroppo, per poter fare coincidere ogni punto con quello antipodale, è necessario che la superficie si autointersechi.

La figura che otteniamo si chiama cross-cap. Se andate sulla pagina di mathworld, trovate una applicazione java che vi permette di esaminare il cross-cap girandolo come vi pare.

Insomma, non si scappa: o ci immaginiamo la sfera in cui due punti sono uno solo, o ci prendiamo il cross-cap con la superficie che interseca sé stessa. Oppure passiamo in quattro dimensioni. TANSTAAFL.

(Direi che possiamo fermarci qua, con il programma di Erlangen)

Erlangen 1872 — Dualità

La magia che fa corrispondere punti a rette e rette a punti si chiama dualità. Ed è una magia molto potente, perché permette di avere teoremi gratis e, cosa forse ancora più importante, permette di avere una visione nuova della geometria: una di quelle esperienze a-ha di cui ha parlato anche il Sommo Divulgatore.

Provo a fare qualche esempio.

Due punti individuano una retta (detto in altri termini: per due punti passa una e una sola retta). Scambiando i punti con le rette, otteniamo la proposizione due rette individuano un punto (cioè: due rette si intersecano sempre in un punto).

Per un punto passano infinite rette, che diventa una retta contiene infiniti punti.

Insomma, ogni teorema può essere trasformato in un altro teorema scambiando tra loro i termini punto e retta. Naturalmente cambiano anche i verbi che vengono usati: un punto appartiene a una retta, una retta passa per un punto, ma la relazione che intercorre tra il punto e la retta è una sola, e viene detta struttura di incidenza.

Vediamo un esempio un po' più corposo.

Dati tre punti allineati A, B e C e altri tre punti allineati a, b e c, allora i punti X, Y e Z, rispettivamente intersezioni delle rette Ab e aB, Ac e aC, Bc e bC, sono anch'essi allineati.

Che diventa, applicando la dualità:

Date tre rette A, B e C incidenti, e altre tre rette a, b e c anch'esse incidenti, allora le rette X, Y e Z, rispettivamente passanti per i punti di intersezione di A con b e di a con B, di A con c e di a con C, di B con c e di b con C sono anch'esse incidenti.

Un altro esempio:

Sono dati due triangoli ABC e A'B'C'. Se le rette AA', BB' e CC' sono incidenti, allora le rette AB e A'B', BC e B'C', CA e C'A' si intersecano rispettivamente in tre punti X, Y e Z che sono allineati.

Vediamo di dualizzarlo:

Sono dati due triangoli ABC e A'B'C'. Se tre punti X, Y e Z sono allineati e, rispettivamente, si trovano sul prolungamento di AB e A'B', BC e B'C', CA e C'A', allora le tre rette AA', BB' e CC' sono incidenti.

Insomma, questo teorema è duale di sé stesso.

Bello, eh?

Erlangen 1872 — È una specie di magia

Un punto ha due coordinate, e fin qua niente di strano: due numeri individuano un punto sul piano cartesiano.

Una retta ha equazione y=mx+q. Per determinare una retta, quindi, bisogna conoscere i due numeri m e q. Due numeri individuano una retta sul piano cartesiano.

Quindi se io scrivo 3 e 14, potrei voler descrivere un punto oppure una retta. Oppure tutte e due.

In realtà le cose non stanno proprio così: non tutte le rette hanno la forma y=mx+q, quelle verticali si scrivono in un'altra maniera: x=k. Ma possiamo evitare il problema passando alle coordinate omogenee.

Ricominciamo: un punto ha tre coordinate, (a,b,c), definite a meno di una costante.

Una retta ha equazione ax+by+c=0, dove i coefficienti a, b e c sono definiti a meno di una costante.

Quindi tre numeri a, b e c definiscono, a meno di una costante moltiplicativa, un punto o, indifferentemente, una retta. O tutte e due.

Detto in un altro modo: ad ogni punto è associata una retta, e ad ogni retta è associato un punto. Il mondo dei punti potrebbe essere trasformato nel mondo delle rette e, viceversa, il mondo delle rette potrebbe diventare quello dei punti. Anche le rette, quindi, hanno delle coordinate, che vengono dette coordinate plückeriane.

Esempio: (3,1,4).

Se le consideriamo come coordinate omogenee di un punto, trasformandole in coordinate cartesiane otteniamo il punto (3/4,1/4).

Se invece le consideriamo come coordinate plückeriane, esse rappresentano la retta 3x+y+4z=0. Ecco qua:

C'è una relazione geometrica tra il punto e la retta: se noi tracciamo, dall'origine O degli assi, la perpendicolare alla retta data, e indichiamo con H il punto di intersezione, risulta che il punto P si trova sulla stessa perpendicolare, in una posizione tale per cui PO è il reciproco di OH.

Viceversa, se partiamo dal punto e tracciamo una retta passante per P e O, la retta cercata sarà ortogonale a PO, e l'intersezione tra le due rette H è tale per cui OH è il reciproco di PO.

E il tutto funziona anche coi punti impropri! A un punto improprio corrisponde una retta passante per l'origine, e viceversa.

Ma tutto questo non basta: consideriamo un'altra coppia punto-retta, per esempio quella identificata dalla terna (-1,2,1). Indichiamo con Q il nuovo punto:

Ora tracciamo la retta passante per P e Q: quale sarà il suo punto associato? Ebbene, non è un punto a caso, ma è l'intersezione tra le due rette che abbiamo già tracciato.

E se le rette sono parallele? Nessun problema, ci sono i punti impropri.

Tutto ciò è meraviglioso.

Glissando

Erlangen 1872 — Esiste una sola conica

Utilizziamo la proiettività della volta scorsa per trasformare qualche conica. Prendiamo la circonferenza di equazione

che è semplicemente la circonferenza con centro nel punto (0,2) e raggio 1 (se volete saltare i calcoli, più giù c'è la figurina che mostra subito la prospettiva). Dobbiamo trasformarla in coordinate omogenee,

e poi applicare la trasformazione scritta l'altra volta, quella che al posto di x sostituisce x' (cioè non fa nulla), al posto di y sostituisce z' e, al posto di z, sostituisce -y'. Ecco il risultato:

che possiamo riscrivere eliminando gli apici, che ora non servono più, svolgendo un po' i calcoli e rimettendo in coordinate cartesiane. Quello che si ottiene è la seguente formula:

che, se vogliamo scrivere in una forma più utile (per chi ricorda qualcosa di geometria analitica), diventa:

una ellisse, insomma, con centro in (0,-2/3), semiasse maggiore uguale a 1 su radice di 3, semiasse minore uguale a 1 su 3.

Per quelli che hanno saltato i calcoli, ecco la figurina: una circonferenza in prospettiva diventa una ellisse.

Direi che sia una cosa abbastanza naturale, se mi è concesso l'ardire.

Ora trasformiamo qualcosa di meno immediato: una parabola. Precisamente, quella di equazione y=x²+1, che diventa yz=x²+z² in coordinate omogenee.

Tralascio i passaggi e scrivo subito il risultato: si ottiene la curva x²+y²+y=0 che, scritta in modo da mettere in evidenza centro e raggio, diventa:

Si tratta di una circonferenza con centro in (0,-1/2) e raggio 1/2. Ecco la figura:

Stranamente, una parabola in prospettiva diventa ancora una circonferenza. Questa volta, però, la circonferenza è tangente all'asse delle x, cioè alla linea di orizzonte, cioè alla retta impropria. Insomma, i due rami di parabola non sono proprio come due rette parallele, ma quasi.

Prima di passare all'iperbole, bisogna aggiungere una considerazione. Abbiamo detto che la proiettività che stiamo usando prende ciò che si trova al di sopra dell'asse x e lo mette in prospettiva nella parte sottostante, avendo cioè l'asse x come orizzonte. Naturalmente la trasformazione lavora anche sui punti che si trovano al di sotto dell'asse delle ascisse, anche se finora non abbiamo (volutamente) mai visto un esempio.

Come dobbiamo interpretare l'azione della proiettività nella parte sottostante l'asse delle x? Ecco, è come se noi ci voltassimo dall'altra parte: se finora abbiamo pensato al disegno in prospettiva di ciò che vediamo davanti a noi, ora aggiungiamo anche il disegno di ciò che si trova dietro di noi.

Faccio due disegni, che è meglio. Nel primo, metto solo una parte dell'iperbole di equazione x²-y²=-1, quella che sta di sopra, al posto giusto. E metto anche la funzione trasformata, che è x²+y²=1.

E fin qua possiamo anche essere d'accordo. Ora aggiungo il ramo inferiore dell'iperbole (che si trova nella zona dove noi disegniamo la prospettiva) e la curva trasformata (che si troverà nella parte sopra all'asse delle x). Ecco:

Abbiamo di nuovo una circonferenza, che questa volta attraversa l'orizzonte, cioè la retta impropria.

Riassunto: la prospettiva è un sistema che ci permette di vedere la retta impropria. Mediante il disegno in prospettiva abbiamo capito che le tre categorie di coniche si differenziano solo per il modo in cui vanno all'infinito, cioè intersecano la retta impropria.

L'ellisse non ci va, la retta impropria la vede solo da lontano. La parabola è tangente alla retta impropria, l'iperbole è secante.

Se noi trattiamo la retta impropria come una retta normale, succede che la forma delle tre curve, che ci appare così diversa nella geometria affine, è invece la stessa: sono tutte e tre curve chiuse.

Nella geometria proiettiva esiste una sola conica.

Non ce la posso fare

Dopo una settimana di lezione, ancora non mi capacito di avere studenti dell'età di mio figlio maggiore.

Erlangen 1872 — Prospettiva

Facciamo un esempio. Prendiamo questa proiettività, dalle equazioni molto semplici:

Dobbiamo interpretare le equazioni in questo modo: noi abbiamo le coordinate (omogenee) di un punto (x,y,z), le inseriamo nelle formule e otteniamo le coordinate del punto trasformato (x',y',z').


Ora prendiamo questi quattro punti: A(-1,1,1), B(1,1,1), C(1,3,1) e D(-1,3,1), e li trasformiamo. Utilizzando le formule della proiettività, otteniamo A'(-1,-1,1), B'(1,-1,1), e fin qua è facile. Quando andiamo a fare i conti per C', risulta (1,-1,3): se ci ricordiamo che le coordinate sono omogenee, e quindi possiamo moltiplicare o dividere ogni termine per una costante arbitraria, possiamo scrivere che C' ha coordinate (1/3,-1/3,1), così lo possiamo rappresentare meglio. Analogamente per D' otteniamo (-1/3,-1/3,1).

Ecco un disegno:

Si capisce come agisce la trasformazione? Prende ciò che si trova al di sopra dell'asse x e lo rappresenta in prospettiva di sotto: in questo caso l'asse x diventa la linea d'orizzonte; le rette parallele BC e AD convergono in un punto. In pratica questa proiettività prende la retta impropria e la sposta al posto dell'asse x.

Ecco un altro esempio:

La figura ABCD è un rettangolo, le cui coordinate sono le seguenti: A(0,1), B(1,3), C(-3,5), D(-4,3). Se volete fare i conti, i punti trasformati sono A'(0,-1), B'(1/3,-1/3), C'(-3/5,-1/5), D'(-4/3,-1/3). Il rettangolo ha i lati opposti paralleli secondo due direzioni diverse, quindi AB e DC si incontrano nello stesso punto improprio, mentre BC e AD si incontrano in un punto improprio diverso (sono quelli che, in disegno tecnico, si chiamano punti di fuga): ecco un ingrandimento della figura in prospettiva.

Bene, trasformare i punti è facile. Ora vorremmo trasformare delle curve. È altrettanto facile purché capiamo una cosa: se la curva ha equazione f(x,y)=0, noi non possiamo prendere i suoi infiniti punti e trasformarli uno per uno, e allora giriamo il problema: prendiamo le equazioni della trasformazione geometrica e le inseriamo nella curva. Occorre quindi un passaggio preliminare, molto semplice: dobbiamo ricavare le coordinate x,y,z in funzione di x',y',z'.

Questa è quindi la trasformazione da usare per trasformare delle curve:

Trasformare alcune coniche sarà molto simpatico.

Erlangen 1872 — Intersezioni con la retta impropria

Abbiamo detto che l'equazione di una conica è una generica equazione di secondo grado in due incognite:

che in coordinate omogenee diventa:

Se ora intersechiamo con la retta impropria (che ha equazione z=0), otteniamo:

che è una equazione di secondo grado facilmente risolvibile con la solita formula. Come succede per tutte le equazioni di secondo grado, sono possibili tre casi:

— due soluzioni reali distinte: in questo caso la conica ha due punti impropri diversi, e quindi è una iperbole;

— due soluzioni reali coincidenti: in questo caso la conica è tangente alla retta impropria, ed è una parabola;

— nessuna soluzione reale: ecco l'ellisse.

Insomma, le coniche si riconoscono dal tipo di intersezione che hanno con la retta impropria. O, se vogliamo, per come vanno all'infinito.

Sarà meglio fare qualche disegnino.