giovedì 29 novembre 2007
mercoledì 28 novembre 2007
Rivoluzione
“Prof, posso fare una domanda?”, chiede Elisa Rivoluzionaria, classe prima.
“Vai”.
“Però non c'entra molto con quello che stiamo facendo...”.
“Mmh”.
“No, perché... bè, no, niente” (ottima tattica).
“Dai, dimmi”.
“Ecco, io non ho mai capito bene una cosa. Perché 3×0 fa 0? Secondo me dovrebbe fare 3. Cioè, se moltiplico 3 per sé stesso 0 volte, rimane un solo 3”.
“Ok, capito. Potrei dirti che prendere un numero zero volte significa non prenderlo, quindi non hai niente, quindi zero, ma immagino che come risposta non ti soddisfi, dico bene?”.
“Eh, in effetti, sì”.
“Allora proviamo con un'altra risposta. Ti ricordi quando, all'inizio dell'anno, abbiamo parlato delle potenze? Di come abbiamo spiegato il significato delle potenze con esponente negativo? Quando diciamo 3-2 non pensiamo alla moltiplicazione di 3 per sé stesso meno due volte, vero?”.
“Eh, no”.
“Avevamo detto che quella era una definizione. Se vuoi che le proprietà delle potenze valgano ancora, 3-2 deve essere uguale a 1/32, giusto?”.
“Sì, mi ricordo”.
“Bene, allora guarda questo”. E scrivo alla lavagna questa uguaglianza:
3×0 = 3×(1-1) = 3×1 - 3×1 = 3 - 3 = 0.
“Vedi? Se vuoi che la proprietà distributiva sia ancora valida, bisogna che tre per zero faccia zero”.
“Ah, che bello! Ho capito!”. Sorrisone, espressione soddisfatta.
“Va meglio questa spiegazione, eh?”.
“Sì. Sa, prof, alle medie avevamo fatto una mezza rivoluzione su questa cosa...”.
“Rivoluzione?”.
“Eh, sì. Noi eravamo del gruppo del 3×0=3”.
“Ma dai. E magari facevate anche le proteste?”.
“Sì, eravamo molto presi, andavamo in giro per i corridoi, avevamo gli striscioni con scritto sopra 3×0=3”.
“Vai”.
“Però non c'entra molto con quello che stiamo facendo...”.
“Mmh”.
“No, perché... bè, no, niente” (ottima tattica).
“Dai, dimmi”.
“Ecco, io non ho mai capito bene una cosa. Perché 3×0 fa 0? Secondo me dovrebbe fare 3. Cioè, se moltiplico 3 per sé stesso 0 volte, rimane un solo 3”.
“Ok, capito. Potrei dirti che prendere un numero zero volte significa non prenderlo, quindi non hai niente, quindi zero, ma immagino che come risposta non ti soddisfi, dico bene?”.
“Eh, in effetti, sì”.
“Allora proviamo con un'altra risposta. Ti ricordi quando, all'inizio dell'anno, abbiamo parlato delle potenze? Di come abbiamo spiegato il significato delle potenze con esponente negativo? Quando diciamo 3-2 non pensiamo alla moltiplicazione di 3 per sé stesso meno due volte, vero?”.
“Eh, no”.
“Avevamo detto che quella era una definizione. Se vuoi che le proprietà delle potenze valgano ancora, 3-2 deve essere uguale a 1/32, giusto?”.
“Sì, mi ricordo”.
“Bene, allora guarda questo”. E scrivo alla lavagna questa uguaglianza:
3×0 = 3×(1-1) = 3×1 - 3×1 = 3 - 3 = 0.
“Vedi? Se vuoi che la proprietà distributiva sia ancora valida, bisogna che tre per zero faccia zero”.
“Ah, che bello! Ho capito!”. Sorrisone, espressione soddisfatta.
“Va meglio questa spiegazione, eh?”.
“Sì. Sa, prof, alle medie avevamo fatto una mezza rivoluzione su questa cosa...”.
“Rivoluzione?”.
“Eh, sì. Noi eravamo del gruppo del 3×0=3”.
“Ma dai. E magari facevate anche le proteste?”.
“Sì, eravamo molto presi, andavamo in giro per i corridoi, avevamo gli striscioni con scritto sopra 3×0=3”.
martedì 27 novembre 2007
Langkofelscharte
Era l'inverno della quarta superiore. I miei mi portarono in settimana bianca, a S. Cristina di Val Gardena. Mi iscrissi alla scuola di sci, e venni assegnato alla sesta classe, quella dei “bravi”.
Dopo tre giorni di lezione il maestro (ho trovato la foto, c'è ancora!) ci portò ai piedi di una montagna e ci disse:
“Vedete lassù? Quello è il Sassolungo, di fianco c'è il Sassopiatto. Lì in mezzo c'è la forcella del Sassolungo: se vi va bene, domani la facciamo”.
Guardando in alto, vedemmo un impianto di risalita che portava alla forcella tra le due cime e, sotto, una pista piena di sassi, interrotta qua e là da alcune reti che forse servivano per fermare le eventuali cadute degli sciatori, o forse per le valanghe, chissà.
“Maestro, ma dobbiamo fare quella pista piena di sassi?”.
“Ah, no, non scendiamo da questa parte, scendiamo dall'altra!”.
“Ma dall'altra parte non ci sono piste!”.
“Appunto”.
La mattina dopo, inquieti (almeno, io lo ero), tornammo all'impianto di risalita. Era una vecchia ovovia, di quelle con cabine da due persone, gialle, dove si deve stare in piedi. Gli sci si infilavano in un portasci all'esterno, si doveva correre per salire, e poi si doveva attendere. Infatti le cabine non si staccavano dalla fune per permettere una salita agevole, e quindi la fune stessa non poteva andare troppo veloce. Forse allora non esistevano ancora impianti di quel tipo, fatto sta che la risalità durò un quarto d'ora. Al giorno d'oggi un tempo d'attesa così lungo, in piedi, al freddo, è impensabile. Allora era abbastanza normale, io ero salito con un tedesco col quale ho scambiato una sola frase: gli dissi che a scuola studiavo tedesco, ma devo averglielo detto così male che lui lasciò perdere ogni tentativo di dialogo.
Intanto la forcella si avvicinava, noi eravamo sospesi su una pista ripidissima, le pareti del Sassolungo e del Sassopiatto erano sempre più vicine, in alto si vedeva un rifugio, nulla si poteva sapere su quello che ci sarebbe stato dall'altra parte.
Arrivati su, congelati, il maestro ci propose di entrare nel rifugio a scaldarci un po'. Tutti accettammo con piacere, e nel breve percorso dalla stazione di arrivo dell'ovovia all'entrata del rifugio riuscii a dare un'occhiata all'“altra parte” della forcella: un nulla bianco. E stretto. Entrai nel rifugio tremando, non solo per il freddo.
Ingurgitata una serie di sostanze dopanti (erano solo le dieci del mattino), ci toccò di lasciare il rifugio, che per me era diventato un nido da non abbandonare per nessun motivo al mondo, e cominciammo la discesa.
“Ora vado avanti io”, ci disse il maestro, “mi fermo laggiù e vi faccio segno di scendere. Scendete uno alla volta, così se cadete vi fermo io”.
Questo fu l'inizio di una discesa meravigliosa, fuori dalle piste, che ci portò fino a valle. Non prendemmo nessun altro impianto, arrivammo in fondo, avremmo dovuto prendere una seggiovia per ritornare al punto di partenza, ma gli impianti erano ormai chiusi. Allora sciammo lungo stradine che, d'estate, erano pedonali in mezzo al paesino, tra la gente che stava passeggiando. Arrivammo alle sette di sera, dopo nove ore di sci.
Un'esperienza che ricordo ancora con orgoglio: quando passo da quelle parti non manco mai di ricordare che “io sono stato sulla forcella del Sassolungo” (tra parentesi, ora mi viene in mente che, il giorno dopo, ci fu la gara di sci della scuola, e io arrivai secondo — ma di questo sono molto meno orgoglioso, tant'è che me l'ero dimenticato).
Ora scopro la storia del mio “ultimo” rifugio.
Dopo tre giorni di lezione il maestro (ho trovato la foto, c'è ancora!) ci portò ai piedi di una montagna e ci disse:
“Vedete lassù? Quello è il Sassolungo, di fianco c'è il Sassopiatto. Lì in mezzo c'è la forcella del Sassolungo: se vi va bene, domani la facciamo”.
Guardando in alto, vedemmo un impianto di risalita che portava alla forcella tra le due cime e, sotto, una pista piena di sassi, interrotta qua e là da alcune reti che forse servivano per fermare le eventuali cadute degli sciatori, o forse per le valanghe, chissà.
“Maestro, ma dobbiamo fare quella pista piena di sassi?”.
“Ah, no, non scendiamo da questa parte, scendiamo dall'altra!”.
“Ma dall'altra parte non ci sono piste!”.
“Appunto”.
La mattina dopo, inquieti (almeno, io lo ero), tornammo all'impianto di risalita. Era una vecchia ovovia, di quelle con cabine da due persone, gialle, dove si deve stare in piedi. Gli sci si infilavano in un portasci all'esterno, si doveva correre per salire, e poi si doveva attendere. Infatti le cabine non si staccavano dalla fune per permettere una salita agevole, e quindi la fune stessa non poteva andare troppo veloce. Forse allora non esistevano ancora impianti di quel tipo, fatto sta che la risalità durò un quarto d'ora. Al giorno d'oggi un tempo d'attesa così lungo, in piedi, al freddo, è impensabile. Allora era abbastanza normale, io ero salito con un tedesco col quale ho scambiato una sola frase: gli dissi che a scuola studiavo tedesco, ma devo averglielo detto così male che lui lasciò perdere ogni tentativo di dialogo.
Intanto la forcella si avvicinava, noi eravamo sospesi su una pista ripidissima, le pareti del Sassolungo e del Sassopiatto erano sempre più vicine, in alto si vedeva un rifugio, nulla si poteva sapere su quello che ci sarebbe stato dall'altra parte.
Arrivati su, congelati, il maestro ci propose di entrare nel rifugio a scaldarci un po'. Tutti accettammo con piacere, e nel breve percorso dalla stazione di arrivo dell'ovovia all'entrata del rifugio riuscii a dare un'occhiata all'“altra parte” della forcella: un nulla bianco. E stretto. Entrai nel rifugio tremando, non solo per il freddo.
Ingurgitata una serie di sostanze dopanti (erano solo le dieci del mattino), ci toccò di lasciare il rifugio, che per me era diventato un nido da non abbandonare per nessun motivo al mondo, e cominciammo la discesa.
“Ora vado avanti io”, ci disse il maestro, “mi fermo laggiù e vi faccio segno di scendere. Scendete uno alla volta, così se cadete vi fermo io”.
Questo fu l'inizio di una discesa meravigliosa, fuori dalle piste, che ci portò fino a valle. Non prendemmo nessun altro impianto, arrivammo in fondo, avremmo dovuto prendere una seggiovia per ritornare al punto di partenza, ma gli impianti erano ormai chiusi. Allora sciammo lungo stradine che, d'estate, erano pedonali in mezzo al paesino, tra la gente che stava passeggiando. Arrivammo alle sette di sera, dopo nove ore di sci.
Un'esperienza che ricordo ancora con orgoglio: quando passo da quelle parti non manco mai di ricordare che “io sono stato sulla forcella del Sassolungo” (tra parentesi, ora mi viene in mente che, il giorno dopo, ci fu la gara di sci della scuola, e io arrivai secondo — ma di questo sono molto meno orgoglioso, tant'è che me l'ero dimenticato).
Ora scopro la storia del mio “ultimo” rifugio.
lunedì 26 novembre 2007
Tare di famiglia
Mia sorella ha partecipato a un corso di tecnica di memorizzazione veloce. In pochi secondi mi ha snocciolato una quarantina di cifre di pi greco.
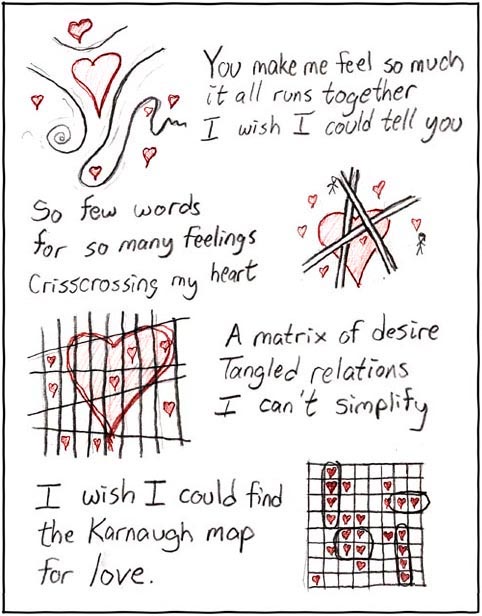
Io ero rimasto a How I wish I could enumerate pi easily (anche se, in realtà, ne so due in più, perché la mia prima calcolatrice aveva un display a dieci cifre).
Io ero rimasto a How I wish I could enumerate pi easily (anche se, in realtà, ne so due in più, perché la mia prima calcolatrice aveva un display a dieci cifre).
venerdì 23 novembre 2007
È dura la sesta ora
“Il quaderno — non c'è”.
“L'esercizio — non lo stai facendo”.
“Attraverso la valvola del termo — non ci si vede”.
“L'esercizio — non lo stai facendo”.
“Attraverso la valvola del termo — non ci si vede”.
giovedì 22 novembre 2007
mercoledì 21 novembre 2007
Tirato in ballo
A lui dà della blogstar, a me invece dello scarso :-)
Scherzi a parte, rispondo all'invito.
1. Chi o cosa ti ha spinto a scrivere un blog?
Un mio studente aveva raccolto le perle pronunciate dai suoi insegnanti durante tutto il triennio. A me è venuta voglia di fare altrettanto (nei confronti degli studenti, però). L'episodio che ha dato l'avvio al tutto è stato quello raccontato nel...
2. Il tuo primo post?
...mio primo post.
3. Il post di cui ti vergogni di più?
Questo, era proprio scarso.
4. Il post di cui sei più fiero?
Non saprei. Stando alle statistiche di lloogg, questo ha funzionato bene. Bè, questo sicuramente deve essere segnalato. E la storia della Cocca. E quello sui giochi di ruolo, con la citazione di Pirandello e il titolo Tolkeniano. E l'apologia dell'insegnamento. E la mia storia telematica, con la citazione di Wargames. Vabbè, basta, potevo fermarmi al non saprei.
5. Per quanto pensi che continuerai a scrivere sul tuo blog?
Mah, è dal 1989 che scrivo da qualche parte - prima fidonet, poi newsgroup, email, blog. Diciamo che potrà cambiare la struttura, ma da qualche parte scriverò sempre.
Scherzi a parte, rispondo all'invito.
1. Chi o cosa ti ha spinto a scrivere un blog?
Un mio studente aveva raccolto le perle pronunciate dai suoi insegnanti durante tutto il triennio. A me è venuta voglia di fare altrettanto (nei confronti degli studenti, però). L'episodio che ha dato l'avvio al tutto è stato quello raccontato nel...
2. Il tuo primo post?
...mio primo post.
3. Il post di cui ti vergogni di più?
Questo, era proprio scarso.
4. Il post di cui sei più fiero?
Non saprei. Stando alle statistiche di lloogg, questo ha funzionato bene. Bè, questo sicuramente deve essere segnalato. E la storia della Cocca. E quello sui giochi di ruolo, con la citazione di Pirandello e il titolo Tolkeniano. E l'apologia dell'insegnamento. E la mia storia telematica, con la citazione di Wargames. Vabbè, basta, potevo fermarmi al non saprei.
5. Per quanto pensi che continuerai a scrivere sul tuo blog?
Mah, è dal 1989 che scrivo da qualche parte - prima fidonet, poi newsgroup, email, blog. Diciamo che potrà cambiare la struttura, ma da qualche parte scriverò sempre.
martedì 20 novembre 2007
lunedì 19 novembre 2007
Qwghlm
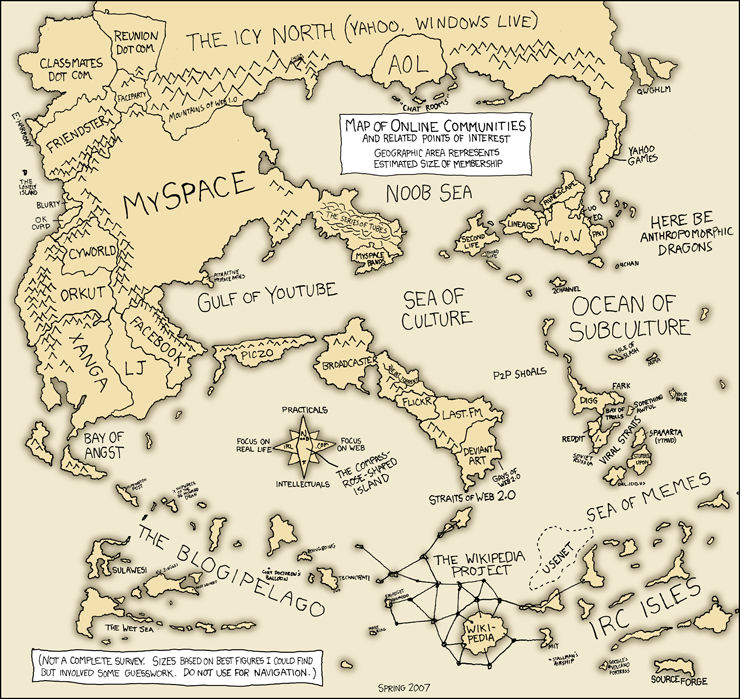
Oggi mi sono impallinato con xkcd... Nella sua Online Communities compare, in alto a destra, una coppia di isolette. Se non riconoscete la citazione, significa che non avete letto questo libro:

E se non avete letto questo libro, non potete dire di aver vissuto.
Prince of Persia
Quanto ci ho giocato a questo gioco...
Uno dei primi ad usare la famosa scheda musicale Adlib (prima si andava solo di pc speaker...). Per l'epoca, la grafica era spettacolare, i movimenti del protagonista erano fluidissimi.
Ecco l'ultimo livello:
(Via AntonioGenna.net blog)
Uno dei primi ad usare la famosa scheda musicale Adlib (prima si andava solo di pc speaker...). Per l'epoca, la grafica era spettacolare, i movimenti del protagonista erano fluidissimi.
Ecco l'ultimo livello:
(Via AntonioGenna.net blog)
domenica 18 novembre 2007
venerdì 16 novembre 2007
Indecisioni
“Allora, ragazzi, su quale asse si misura il coseno? Chi è che ha detto icsilon?”.
giovedì 15 novembre 2007
Teorema
Ipotesi
Tesi
Dimostrazione
- Il mio nucleo familiare è composto da cinque persone
- I quattro quinti dei componenti sono di sesso maschile
- Il quinto rimanente appartiene alla categoria moglie.
- Il figlio più grande frequenta la prima media.
- La scuola frequentata dal figlio più grande attiva ogni anno dei laboratori educativi pomeridiani, dove esperti e genitori volontari propongono attività di vario tipo (per esempio: cucina, danza, riparazione biciclette, lettura, modellismo).
- Il quinto femminile della famiglia ha pronunciato la frase: “perché non fai qualcosa anche tu?”.
- Alla domanda precedente ho risposto: “no, no, assolutamente no”.
- Ieri c'è stata una riunione fatta dagli insegnanti organizzatori del progetto per presentarlo ai nuovi genitori e per raccogliere nuove disponibilità.
Tesi
- La scuola frequentata dal figlio maggiore quest'anno offrirà un nuovo laboratorio dal titolo Enigmi e giochi matematici.
Dimostrazione
- L'ovvia dimostrazione è lasciata al lettore per esercizio.
lunedì 12 novembre 2007
Mai più senza
Questa mattina, andando a scuola in bicicletta, ho provato Sports Tracker, un programmino della Nokia che, usato assieme a un ricevitore GPS, memorizza il percorso e le velocità fatte, crea un riepilogo con tante belle informazioni utili, un grafico della velocità in funzione del tempo, un altro grafico della velocità in funzione della strada percorsa, uno dell'altitudine, e permette di esportare il tutto sotto forma di file leggibile su google earth. Una cosa assolutamente inutile e, quindi, meravigliosa.
domenica 11 novembre 2007
Calunnie
Un'amica dei miei figli, che frequenta la scuola dove insegno, sostiene che tra gli studenti io abbia la fama di essere cattivissimo.
Spero che mi assegnino un'ora di supplenza nella sua classe.
Spero che mi assegnino un'ora di supplenza nella sua classe.
mercoledì 7 novembre 2007
Tavole della legge
Mentre sgridavo quelli di seconda, che dopo quattro ore di lezione erano riusciti ad accumulare tre note disciplinari, ho sentito pronunciare il mio nome.
Allora mi è venuta la geniale idea di dire: “non nominate il mio nome invano!”.
Subito dopo c'è stato un coro di “non avrai altro Dio fuori che la matematica”, “ricordati di santificare la matematica”, “onora la matematica”...
Sono riuscito a fermarli prima che arrivassero al sesto comandamento.
Allora mi è venuta la geniale idea di dire: “non nominate il mio nome invano!”.
Subito dopo c'è stato un coro di “non avrai altro Dio fuori che la matematica”, “ricordati di santificare la matematica”, “onora la matematica”...
Sono riuscito a fermarli prima che arrivassero al sesto comandamento.
martedì 6 novembre 2007
lunedì 5 novembre 2007
I'll be back
Google annuncia l'ingresso nella telefonia mobile, presentando un sistema operativo per telefoni cellulari basato su linux e chiamato Android. Qualcuno ha immediatamente pensato a Skynet. Se prendono Sarah Connor come testimonial stracciano subito la concorrenza.
sabato 3 novembre 2007
La soluzione della sequenza numerica
Il fattoriale di un numero n si indica con n! ed è il prodotto di tutti i numeri naturali compresi tra n e 1. Per esempio:
1! = 1.
2! = 2·1 = 2.
3! = 3·2·1 = 6.
4! = 4·3·2·1 = 24.
(Naturalmente moltiplicare per 1 non serve a niente, ma una definizione che si fermi a 2 non sarebbe elegante. Anzi, esisterebbe anche 0! che, per evitare di specificare casi particolari in alcune formule, è definito uguale a 1)
Bene, se analizziamo la sequenza proposta un paio di post fa, osserviamo che all'inizio sembra una cosa tranquilla, e poi risulta evidentemente il prodotto di una malata mente matematica. L'ultimo numero è grosso, e se proviamo a scomporlo in fattori scopriamo che contiene tutti i numeri primi fino a 719. Questo dovrebbe farci venire in mente il numero 720, pari a 6!. Ma anche 6 è il fattoriale di 3. E quindi potremmo scrivere che 720=6!=3!!. E poi potremmo calcolare il fattoriale di 720, ottenendo proprio quel numero gigantesco. Allora dovremmo capire che la sequenza è la seguente:
0
1!
2!!
3!!!
e quindi il numero successivo è 4!!!!. Il calcolo del quale è lasciato al lettore volonteroso.
1! = 1.
2! = 2·1 = 2.
3! = 3·2·1 = 6.
4! = 4·3·2·1 = 24.
(Naturalmente moltiplicare per 1 non serve a niente, ma una definizione che si fermi a 2 non sarebbe elegante. Anzi, esisterebbe anche 0! che, per evitare di specificare casi particolari in alcune formule, è definito uguale a 1)
Bene, se analizziamo la sequenza proposta un paio di post fa, osserviamo che all'inizio sembra una cosa tranquilla, e poi risulta evidentemente il prodotto di una malata mente matematica. L'ultimo numero è grosso, e se proviamo a scomporlo in fattori scopriamo che contiene tutti i numeri primi fino a 719. Questo dovrebbe farci venire in mente il numero 720, pari a 6!. Ma anche 6 è il fattoriale di 3. E quindi potremmo scrivere che 720=6!=3!!. E poi potremmo calcolare il fattoriale di 720, ottenendo proprio quel numero gigantesco. Allora dovremmo capire che la sequenza è la seguente:
0
1!
2!!
3!!!
e quindi il numero successivo è 4!!!!. Il calcolo del quale è lasciato al lettore volonteroso.
Iscriviti a:
Commenti (Atom)

