«Fenomeno…».
«Lo sai che Gauss è il Chuck Norris della matematica».
«Voi. Siete. Pazzi».
«Bé, comunque la dimostrazione di Gauss è complicatina. Cominciamo dalla figura».
«Mh, hai colorato i vertici con due colori, perché?».
«Eh, perché questa volta non possiamo accoppiare a due a due le radici e costruire un'equazione. Dato che abbiamo 8 coppie, avremmo 8 incognite, e un'equazione di ottavo grado non è molto gestibile. Gauss allora fa una serie di raggruppamenti: il primo è quello che vedi in figura: le radici rosse vanno sommate tra loro, e quelle blu anche».
«Quindi Gauss fa una cosa del genere?».
y1 = R+R16+R2+R15+R4+R13+R8+R9,
y2 = R3+R14+R5+R12+R6+R11+R7+R10.
«Esatto».
«Ma perché?».
«Aspetta e vedrai. Per prima cosa bisogna calcolare y1+y2».
«Bé, questo è facile: è la somma di tutti gli R, vale -1. Ormai ho imparato».
«Molto bene. Ora bisogna calcolare y1y2».
«Uhm, qua mi sa che non si finisce più… potresti dirmi direttamente il risultato».
«Viene -4».
«Oh, bene. Immagino che ora si debba costruire un'equazione che abbia come soluzione questi due valori».
«Esatto, sai farlo?».
«Certo: y2+y-4 = 0».
«Bene. Vorrei farti presente che non abbiamo ancora risolto il problema, perché la conoscenza di questi due valori di y non ci consente ancora di costruire R. Per poter avere R direttamente, avremmo dovuto utilizzare solo la somma di R + R16, ad esempio, in analogia con quanto avevamo fatto per il pentagono».
«Ok, allora come andiamo avanti?».
«Facciamo una nuova costruzione:».
z1 = R+R16+R4+R13,
z2 = R2+R15+R8+R9.
«È come se avessimo spezzato a metà y1: sono gli stessi elementi, divisi in due gruppi».
«Proprio così, quindi z1+z2 è uguale a y1».
«Ma perché abbiamo suddiviso proprio y1?».
«No, non c'è niente di speciale in y1, ora facciamo la stessa cosa con y2. Costruiamo altre due variabili:».
w1 = R3+R14+R5+R12,
w2 = R6+R11+R7+R10.
«Ah. Qui abbiamo che w1+w2 = y2».
«Giusto. E ti dirò anche che z1z2 = -1, e pure w1w2 = -1».
«Grazie per avermi risparmiato i calcoli. A questo punto suppongo che si debbano costruire altre due equazioni».
«Già. Una avente come soluzioni le due z…».
«Che sarà z2-y1z-1 = 0».
«E l'altra avente come soluzioni le due w».
«Eccola: w2-y2w-1 = 0».
«Ma non siamo ancora arrivati: conoscere i valori delle z o delle w non è sufficiente, non ci permette di trovare R».
«E quindi?».
«E quindi facciamo un'altra costruzione:».
v1 = R+R16,
v2 = R4+R13.
«Gulp, non si finisce più».
«Pensa a Gauss, che ha avuto l'illuminazione mentre era in vacanza».
«Roba da matti. Immagino che si debba costruire un'altra equazione, vero?».
«Eh, sì».
«Però devi dirmi quanto valgono la somma e il prodotto delle v».
«La somma è ovvia, no?».
«Sì, è vero, v1+v2 = z1».
«Bene, ed ecco il genio di Gauss: il prodotto v1v2 = w1».
«Magari ci è arrivato senza nemmeno fare qualche prova su un foglio di carta?».
«Questo la storia non lo dice. Comunque lui ci è arrivato, e ora puoi costruire una nuova equazione».
«Ecco qua: v2-z1v+w1 = 0».
«E questa ha come soluzioni v1 e v2. Ora ti faccio notare che v1 è il termine che ci interessa: è la somma di R + R16: da v1 possiamo ricavare finalmente R. Giusto per essere espliciti fino in fondo, R è una soluzione di r2-v1r+1 = 0».
«L'ultimo termine dell'equazione è 1 perché è uguale al prodotto di R per R16, vero?».
«Esatto. Quindi, per trovare R, dobbiamo risolvere una serie di equazioni di secondo grado. Te le riassumo, risparmiandoti le varie considerazioni che si devono fare sui segni, per fare in modo che R sia proprio la radice dell'unità che vogliamo noi, e non una delle altre 15».
«Ok, vai».
«Primo passaggio: y1 = (√17 - 1)/2».
«Ok».
«Secondo passaggio: y2 = (-√17 -1)/2».
«Ah, giusto, ci serve anche y2 per poter trovare w».
«Esatto. Terzo passaggio: z1 = y1/2 + √(1+y12/4)».
«Carino».
«Quarto passaggio: w1 = y2/2 + √(1+y22/4)».
«Finito?».
«Quasi: ora ci basta trovare v1, che è la radice maggiore dell'equazione v2-z1v+w1 = 0. A questo punto abbiamo R».
«Mamma mia. Ma alla fine quanto risulta, questo benedetto lato dell'eptadecagono?».
«Risulta questo:».
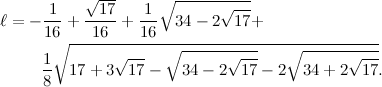
9 commenti:
la costruzione grafica è ipnotizzante :-)
L'animazione è spettacolare :O
Courtesy of wikipedia, naturalmente
Grazie di questo post!
Giovanni
Prego :-)
P.S. Gauss ha anche esplicitato la costruzione del 65537-gono oppure ha scritto "lasciamo la costruzione del 65537-gono al lettore come esercizio"? :-)
Non è stato Gauss, ma qualcuno l'ha fatto, roba da matti. Vai alla puntata 24 che ci sono i link...
Grazie di nuovo. Sto leggendo i tuoi ultimi post e ancora non ci ero arrivato.
Aiutooooooooooooooooooo! Io di matematica non ci capisco niente, ma il compasso mi ha ipnotizzatoooooo!
Posta un commento