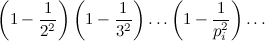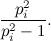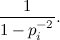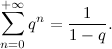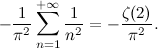Crivelli — 4: Atkin

«L'idea che sta sotto al crivello di Atkin, che sarebbe il crivello che migliora quello di Eratostene, è questa: invece di utilizzare la forma quadratica xy, se ne utilizzano delle altre per le quali i calcoli sono più rapidi».

«Quali?».

«Atkin e Bernstein, i due che hanno pubblicato il loro studio sul nuovo crivello, ne hanno proposte tre, anche se dicono che se ne potrebbero usare delle altre».

«Addirittura tre».

«Eh, sì. Allora, le cose stanno così: tutto è riferito al modulo 60, i numeri vengono divisi in categorie in base al resto della divisione con 60».

«Quindi abbiamo 60 categorie».

«Ora le riduciamo un po', però. Dobbiamo arrivare a tre».

«Bene».

«Prima di tutto, tutti i resti pari li mettiamo nella stessa categoria».

«Perché?».

«Indichiamo con 2N il resto della divisione con 60: posso scrivere 2N perché immagino che sia pari. Allora questi numeri possono essere scritti come 60h+2N, e vedi subito che sono divisibili per 2. Quindi non sono primi (a parte 2, naturalmente)».

«Ah, giusto. Ma allora nella stessa categoria ci possiamo mettere anche quei numeri che hanno resto 3 e 5, per lo stesso motivo».

«Infatti, è così. E questa categoria non ci interessa: non contiene numeri primi, e quindi non la consideriamo più. Rimangono allora questi resti, coi quali costruiremo tre categorie interessanti:».

1, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 49, 53, 59.

«E cosa ci facciamo?».

«Raggruppiamo anche questi: come ti dicevo, in tre classi diverse».

«Come sono fatte?».

«Eh, qui cominciano le cose strane. Per poter usare tre teoremi che ti racconterò dopo, le classi sono fatte così: nella prima ci vanno tutti i numeri uguali a 1 modulo 4».

«Vediamo, dovrebbero essere questi: 1, 13, 17, 29, 37, 41, 49, 53».

«Esatto. Nella seconda classe ci vanno i numeri uguali a 7 modulo 12».

«Mh, sono 7, 19, 31, 43».

«Proprio loro. Nella terza e ultima classe ci vanno i numeri uguali a 11 modulo 12».

«Sono i rimanenti: 11, 23, 47, 59».

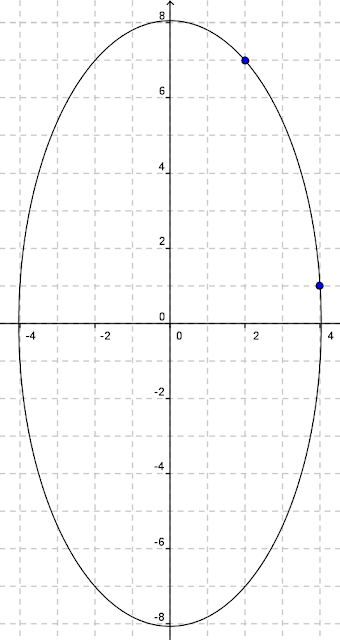
«Bene. Ora, prima di enunciarti il primo teorema ti faccio una figura. Prendiamo un numero della prima classe, per esempio 13. Eccoti il grafico di 4x² + y² = 13».

«Vedo che hai evidenziato un punto».

«Sì, in realtà ce ne sono quattro, simmetrici. Uno solo è quello con coordinate intere positive. Ora, prima di  trarre delle conclusioni, eccoti un altro numero, sempre uguale a 1 modulo 4: 65».

«Perché così grande?».

«Prima il grafico, poi ti spiego:».

«Uh, due punti».

«Sì, il teorema dice che se p è primo e non contiene fattori primi elevati al quadrato (lo so che è una condizione inutile, ma ci servirà dopo per costruire l'algoritmo) allora il numero di punti a coordinate intere positive che stanno sull'ellisse è dispari, e viceversa».

«Ah. E perché hai scelto proprio 65?».

«Perché coi valori minori di 65 gli unici esempi che riuscivo a farti erano di ellissi con zero punti a coordinate intere positive. Zero non è dispari, quindi il teorema funziona, ma c'era poco da disegnare».

«Va bene. Quindi l'algoritmo si deve occupare di contare i punti che stanno su quell'ellisse?».

«Esatto. Poi, dopo che lo ha fatto, deve togliere i valori che contengono fattori primi elevati al quadrato».

«Va bene. Questo però è quello che succede con la prima classe di numeri. Ce ne sono altre due, no?».

«Certo. Per la seconda, quella composta da numeri uguali a 7 modulo 12, vale lo stesso tipo di teorema, ma cambia la curva. Questa volta l'equazione da utilizzare è 3x² + y² = p».

«Mh, facciamo una prova».

«Eccoti la curva con p=7».

«Un solo punto. Vediamo che succede con un numero non primo?».

«Certo. Eccoti p=91».

«Due punti. Anche qui hai dovuto scegliere 91 perché coi numeri più piccoli non avresti trovato punti?».

«Esatto».

«Rimane la terza categoria, allora».

«Sì, quella dei numeri uguali a 11 modulo 12. Questa volta la curva da considerare è diversa, si tratta dell'iperbole di equazione 3x²-y² = p. E, attenzione, solo quando x è maggiore di y, quindi in una zona limitata».

«Mh, vediamo i grafici».

«Questo è con p=11. Ho rappresentato anche la retta y = x: la zona che dobbiamo analizzare si trova al di sotto di quella retta, nel primo quadrante».

«Anche qui, un solo punto».

«E questo con p=143».

«Ah, vedo che hai rappresentato solo il primo quadrante».

«Eh, sì, altrimenti non si sarebbe vista bene la griglia. Ed ecco fatto, tutti i numeri ricadono in queste categorie, si tratta di contare quanti sono i punti a coordinate intere positive che stanno sulle curve — e, nel caso dell'iperbole, hanno ascissa maggiore dell'ordinata — e, se questi sono in numero dispari e se il numero che stiamo analizzando non contiene fattori al quadrato, allora è primo».

«Bleah».

«Sì, lo so, è complicato, ma è a questo che ci ha portati l'astrazione del crivello di Eratostene. Siamo partiti da un semplicissimo sistema di conteggio di numeri su una griglia, e siamo arrivati a contare punti su curve. Ma naturalmente i due autori dell'articolo non hanno mai parlato di curve, né mostrato dei grafici».

«Naturalmente».

«Loro parlano di domini a ideali principali, di forme quadratiche, di semigruppi quoziente, di mappe logaritmiche. Roba che per capirla bene servirebbe un intero corso di algebra. Chissà, forse si può trovare un metodo meno astratto di quello usato da Atkin e Bernstein per dimostrare i teoremi che vengono usati nel loro articolo».

«Dici quelli relativi alle due ellissi e all'iperbole?».

«Sì, quelli. Ti confesso che, dopo averci provato per un po', ci ho rinunciato».

«Ahi, ahi».

«Mi è bastato intuire come stavano le cose, e mi sono fidato. Del resto gli autori dicono che sono teoremi standard, e che li hanno inseriti nel loro lavoro solo per un senso di completezza. Comunque, danno per sottintese mille cose, sono dimostrazioni molto compresse. Ma, se vuoi, trovi tutto qui».

«No, grazie, mi fido anche io».

«Per concludere, Bernstein ha fatto una cosa carina: ha scritto una serie di programmi che tutti possono prelevare ed utilizzare. Io l'ho fatto, e devo dire che sono velocissimi. Sono qui».

«Ma, rispetto al crivello di Eratostene, c'è questo gran vantaggio?».

«Ti dirò, questo criterio non è così tanto più veloce. Gli autori hanno fatto una prova: per trovare tutti i numeri primi fino a N = 10⁹ la loro implementazione del crivello di Eratostene ha impiegato circa 3.3·10⁹ cicli, mentre quella del loro crivello ne ha impiegati 2.5·10⁹».

«Quindi siamo sempre nell'ordine di N».

«In realtà l'ordine è N/log(log(N)). E questo è il meglio che oggi riusciamo a fare».

---

Se qualcuno volesse provare a cercare una dimostrazione decente dei teoremi che ho indicato qua sopra, si tratta dei numeri 6.1, 6.2 e 6.3 a pagina 1028 di questo articolo. Si potrebbe forse ragionare sugli interi di Gauss.

Crivelli — 3: contare i punti su una griglia

«Allora, dobbiamo astrarre il crivello di Eratostene?».

«Esatto. Ragioniamo in questo modo: cosa significa che un numero è primo?».

«Che ha solo due divisori distinti, giusto?».

«Ottimo, vedo che ti ricordi».

«Certo che mi ricordo!».

«Va bene. Quindi un numero che non è primo ha più di due divisori distinti».

«Certo».

«Quindi i numeri primi sono tali per cui l'equazione xy = p ha due sole soluzioni».

«Ecco che complichiamo…».

«Eh, sì. Mentre per i numeri non primi l'equazione xy = p ha più di due soluzioni».

«Aspetta un momento: dici che per i numeri primi quell'equazione ha solo due soluzioni perché puoi scambiare di posto x e y, vero? Cioè, 7 è uguale a 1 moltiplicato 7 oppure a 7 moltiplicato 1. Ho capito bene?».

«Hai capito benissimo. Ora, che curva è quella che ha equazione xy = p, con p costante, x e y variabili?».

«Una… iperbole?».

«Ottimo. Allora guarda come ti traduco la definizione di numero primo: un numero p è primo se esistono solo due punti a coordinate intere positive che appartengono all'iperbole xy = p».

«Mamma mia, che depravazione mentale. Comunque è giusto, sì».

«E, al contrario del mio prof di geometria, io ti faccio anche un disegno, con p = 5».

«Bello, hai disegnato la griglia dei numeri interi».

«Già, come vedi gli unici punti della griglia che vengono toccati dall'iperbole sono (1,5) e (5,1)».

«Carino».

«Se invece il numero non è primo, i punti che vengono toccati sono più di due. Ecco per esempio xy = 12».

«Sei punti».

«Sì, saranno sempre in numero pari, a causa della simmetria; a meno che il numero non sia un quadrato: in quel caso sono dispari».

«Ok. Fin qua ci sono».

«Bene, allora diciamo che il crivello di Eratostene funziona contando i numeri interi positivi che sono soluzioni dell'equazione xy = p, o, per dirla come dicono i Veri Matematici, funziona analizzando i valori della forma quadratica riducibile xy».

«Ed ecco l'astrazione incomprensibile. I Veri Matematici fanno almeno la figurina dell'iperbole, per fare capire di cosa si sta parlando?».

«Naturalmente no».

«Capirai».

«E ora che abbiamo astratto, ragioniamo in questo modo: potremmo forse cambiare la forma quadratica che stiamo utilizzando, per velocizzare un po' i conti?».

«Boh? Possiamo?».

«Possiamo, ma complichiamo. La semplicità del crivello si perde un po'».

Crivelli — 2: astrazioni

«Complicazioni che ci porteranno a scorgere una piccola parte di ciò che genera le ombre che di solito osserviamo? Cosa dici?».

«Forse ho esagerato un po'».

«Direi. Ma a cosa ti riferivi?».

«Mi è venuta in mente una sensazione che ho provato, a volte, quando facevo l'università».

«Cioè?».

«C'era questo libro di geometria, tutto scritto a mano».

«In che senso, a mano?».

«Proprio nel senso che era scritto a mano, in corsivo, in bella calligrafia».

«Ma dai!».

«Davvero. Un'opera d'arte… Era un bel libro, ben organizzato, nei primi capitoli c'erano tutte le basi per poi poter affrontare il resto, non avevi bisogno d'altro. Solo che era incomprensibile».

«Andiamo bene».

«Non nel senso che fosse scritto male, eh. Era proprio la geometria ad essere incomprensibile».

«Figure astruse che dovevi studiarti per ore, prima di capire come fossero fatte?».

«Neanche una figura».

«Eh? Ma come? Un libro di geometria, hai detto?».

«Sì».

«Senza figure».

«Eh».

«Mi sembra di essere in un altro mondo. La geometria non dovrebbe essere fatta con le figure? E allora?».

«Capisci cosa intendo quando dico che era incomprensibile? Non mi aspettavo che fosse così, geometria. E, da quanto sento, questo è l'impatto che la materia ha con tutti gli studenti».

«Quindi quella dei Veri Geometri è una categoria di gente ancora più fuori di testa dei Veri Matematici Generici».

«Questo è quello che pensano in molti, sì».

«Andiamo bene. E allora, cos'è successo con quel libro?».

«È successo che ho dovuto studiarlo, naturalmente. E, per capirlo, dovevo sempre ricollegare le cose astrattissime di cui parlava a ciò che già conoscevo, grazie ai miei studi precedenti».

«Immagino che non fosse una cosa semplice».

«Neanche un po'. Ogni tanto arrivava l'illuminazione, riuscivi a collegare tutto, e ti sembrava di aver raggiunto un livello di consapevolezza che prima non avevi».

«Ma, per esempio?».

«Per esempio, all'inizio della geometria si fa della gran algebra lineare».

«Mi pare ovvio, si chiama geometria, studi dell'algebra. Non fa una piega. Del resto, c'è la parola lineare che mi fa capire che è geometria».

«Eh, non ti sbagli di molto… Comunque, algebra lineare significa matrici. E le matrici hanno delle strane operazioni. E mentre me le studiavo, e cercavo di capire perché dovessero essere fatte proprio in quel modo, a un certo punto mi sono detto: "ma se prendo una matrice formata da una riga e una colonna, ho un numero! Allora tutti i numeri sono matrici! Il mondo è fatto di matrici, e i numeri sono solo casi particolari! Tutto quello che ho studiato era un caso particolare del caso generale. Ora vedo! Ora so! È bellissimo!"».

«Poi sono arrivati, sì?».

«Chi?».

«I medici».

«No, parlavo tra me e me, non mi sono messo a urlare per strada».

«Hai fatto bene».

«Per farti un esempio meno stupido, ricordi quando abbiamo parlato di trasformazioni del piano e di coordinate omogenee?».

«Certo, quella era geometria, c'erano le figure, mi ricordo. Avevo anche capito, le coordinate omogenee erano quelle che mi permettevano di parlare di punti impropri, cioè punti all'infinito».

«Bene. Ora ti faccio vedere la versione dei Veri Geometri».

«Non si capisce niente».

«Esatto. Quella è una pagina del famigerato capitolo IX, dal titolo Relazioni fra le strutture vettoriali, affini e proiettive. Diciannove pagine infernali».

«E tu le hai capite».

«A suo tempo, sì. E quando riuscivo a collegare quella roba con le mie conoscenze, mi sembrava di capire davvero. Mi dicevo: ma allora le cose stanno così. Mi sentivo un eletto che poteva dare un'occhiata alle cose, e non alle loro ombre. Mi sembrava di vedere con gli occhi di Dio».

«Ehm».

«Eh».

«Poi sei guarito?».

«Poi sono diventato insegnante: in un certo senso sono guarito. Perché è bellissimo partire dalle basi e arrivare a un tale livello di astrazione per cui tutto è inserito in un unico concetto, ma poi bisogna anche ridiscendere a valle e fare comprendere le cose, spiegarle, fare qualche maledetto disegno, santo cielo».

«Eh eh».

«Voglio dire, ammiro le menti degli autori di quel libro (uno dei quali era anche il mio insegnante di geometria), ma le loro capacità didattiche non è che fossero quella gran cosa».

«No, eh?».

«No, decisamente. Per esempio lui, dico il prof di geometria, non usava mai il cancellino, scriveva dove trovava posto».

«Benissimo. Del resto, uno che insegna geometria non deve mai usare la lavagna per fare i disegni».

«Infatti. Una volta, prima delle vacanze di Natale, qualcuno disegnò un albero di Natale alla lavagna. Lui cominciò a scrivere le formule sulla lavagna, e in quella lezione ne doveva scrivere molte».

«E non ha cancellato?».

«Assolutamente no, ha cominciato a scrivere dentro all'albero».

«Incredibile».

«E non è finita qua. Quella volta le formule erano così tante che, alla fine, ha dovuto prendere in mano il cancellino».

«Colpo di scena».

«Da tutta l'aula si è alzato un mormorio».

«Eh eh».

«Poi ha appoggiato il cancellino alla lavagna, in un punto centrale, e l'ha mosso per un venti-venticinque centimetri».

«Quanto bastava per l'ultima formula».

«Già. Ma non ha fatto come fanno le persone normali, che appoggiano il cancellino e poi lo muovono un po', in modo da tirare via il gesso. No, lui ha semplicemente appoggiato e spostato, poi l'ha messo via».

«E che risultato ha ottenuto?».

«Ha creato un bel rettangolo bianco e polveroso sulla lavagna. Poi ci ha scritto sopra l'ultima formula, perfettamente mimetizzata tra il gesso. Formula bianca su sfondo bianco, suprematismo matematico».

«Tutto ciò ha dell'incredibile, se uno non pensa che si sta parlando di Veri Matematici».

«Già».

«Ma riguardo al crivello di Eratostene? Cosa c'entra questo discorso con quanto abbiamo detto finora?».

«Per migliorare il crivello, dobbiamo prima astrarre, complicare le cose, e poi cambiarle. Non sarà facile».

Crivelli — 1: Eratostene

Il problema della generazione dei numeri primi è stato studiato da eserciti di matematici (e di informatici), ma non si è ancora giunti a una risoluzione definitiva. Questo perché non sappiamo ancora come generarli, questi benedetti numeri primi, senza sprecare tempo: sappiamo riconoscerli, ma non conosciamo una semplice formula che ci permetta di calcolare l'n-esimo numero primo di colpo (e nemmeno il prossimo numero primo).

Dobbiamo arrangiarci: dobbiamo spulciare l'elenco dei numeri e scartare, nel modo più veloce possibile, i numeri che non sono primi; ovviamente quelli che rimarranno saranno i primi che stiamo cercando. Tutto qua.

«Sembra facile».

«Lo è, almeno all'inizio».

«Capirai…».

«Dico davvero: il più semplice sistema per generare numeri primi si chiama crivello di Eratostene».

«Crivello».

«Sì, si chiama così. Se vuoi, setaccio. Prende tutti i numeri da 1 fino a N, e separa quelli buoni da quelli cattivi».

«E come fa?».

«In un modo semplicissimo: prima di tutto, non parte davvero da 1, parte da 2».

«Va bene, sappiamo che 1 non è un numero primo».

«E poi procede così: legge il primo numero della lista…».

«Cioè 2».

«All'inizio è 2, poi l'algoritmo va avanti sempre alla stessa maniera. Per questo dico che prende il primo numero della lista: la prima volta è 2, poi però questo numero cambierà».

«Ok. Dopo aver preso il primo numero della lista, cosa fa?».

«Lo lascia stare lì dov'è, lo dichiara primo, ma cancella tutti i numeri che lo seguono e che sono suoi multipli».

«Cioè cancella 4, 6, 8, eccetera?».

«Esatto. Possiamo dire che, dato che il primo numero è 2, l'algoritmo procede a salti di lunghezza 2 e cancella tutto quello che trova».

«Sembra una cosa rapida».

«Molto rapida: non devi fare nessun tipo di operazione, solo saltare avanti e cancellare».

«Bene, e arrivati alla fine cosa succede?».

«Si ricomincia da capo, passando al successivo numero della lista che non è stato cancellato».

«Cioè 3».

«Esatto. E si va avanti a passi di 3, cancellando tutto quello che si trova».

«Ma il 6 era già stato cancellato prima».

«Non importa, il suo posto è sempre lì, e se cancelliamo due volte non succede niente. Sprechiamo tempo, in realtà, ma non sbagliamo».

«Ho capito. Poi si passa al 4».

«Eh, no».

«Ah, giusto, il 4 è già stato cancellato prima. Allora c'è il 5, poi ci sarà il 7, e così via».

«Esatto. I numeri che incontri sono i numeri primi, e cancelli tutti i loro multipli».

«Semplice».

«Nella realtà ci sono poi tante piccole ottimizzazioni che lo velocizzano un po'».

«Ah. Robe complicate?».

«Non tanto. Ad esempio, invece di partire dal primo numero della lista si può partire dal suo quadrato, e procedere poi a salti».

«Perché».

«Immagina di essere arrivato al numero 11».

«Il quadrato è 121».

«Certo. In teoria dovresti partire da 11 e eliminare tutti i suoi multipli».

«Il primo è 22, allora».

«Giusto, uguale a 11 per 2».

«Ah, ho capito! Dato che è multiplo di 2, è già stato eliminato prima!».

«Esatto. Poi ci sarebbe 33…».

«Che è stato eliminato quando sono stati cancellati tutti i multipli di 3. Ci sono: il primo numero da considerare è 11 per 11, cioè 121».

«Benissimo. Un altro trucchetto è quello di elencare solo i numeri dispari, tanto sappiamo che i numeri pari, a parte 2, non sono primi. Poi però si procede a salti di ampiezza doppia».

«Mh, perché?».

«Pensa al numero 3: se procedi a passi di ampiezza 3 ottieni 6, 9, 12, 15, e così via. Vedi che un termine ogni due è pari».

«Ed è già stato eliminato dalla lista! Ho capito».

«Questo metodo può poi essere generalizzato utilizzando la cosiddetta wheel factorization».

«Che sarebbe?».

«Si fa prima a fare un disegno che a spiegarlo:».

«Dovrei capire?».

«Guarda bene: è stato scelto come base il numero 30, e tutti i numeri sono stati scritti in cerchio».

«Vedo che il primo cerchio contiene tutti i numeri da 1 a 30, infatti».

«Esatto. Poi il secondo quelli da 31 a 60, e così via».

«Ah, giusto. In pratica li hai raggruppati secondo il resto della divisione modulo 30».

«Benissimo! Vedo che ti ricordi qualcosa, alla fine!».

«Eh, sì. Devo dire che mi hanno aiutato quelle uguaglianze scritte in alto a destra: ho riconosciuto la divisione per 30».

«Proprio così: vedi che ad esempio c'è scritto che 94 è uguale al prodotto di 3 per 30, più 4».

«Sì: vuol dire che 94 diviso 30 ha come quoziente 3 e resto 4».

«Perfetto. A noi interessano i resti: i soli resti che possono generare numeri primi sono 1, 7, 11, 13, 17, 19, 23 e 29».

«Mi sfugge il motivo per cui 3 e 5 sono esclusi dalla lista: quelli sono numeri primi».

«Certo, e il programma ne terrà conto. Ma ogni altro numero che ha resto 3 oppure 5 nella divisione per 30 non sarà primo».

«Mh, fammi capire».

«Un numero che ha resto 3, ad esempio, si può scrivere come 30h+3, cioè 3(10h+1)».

«Ah, certo: è multiplo di 3».

«Esatto. E un numero che ha resto 5 sarà 30k+5, uguale a 5(6k+1)».

«Multiplo di 5».

«Quindi i possibili numeri primi possono trovarsi solo nelle zone non colorate di giallo nella figura».

«Bello. Ma come facciamo con il crivello? Se, quando abbiamo tolto i multipli di 2, abbiamo detto che potevamo procedere a salti di ampiezza 2, ora come funziona?».

«Ecco, ora è più difficile, in effetti. Funziona in questo modo: prima di tutto, indichiamo con k_i i numeri interessanti, cioè i nostri 1, 7, 11, 13, 17, eccetera, fino a 29».

«Bene».

«E indichiamo con M il numero che ha generato la ruota».

«Cioè 30».

«Esatto. Allora, se stiamo analizzando un numero primo p e vogliamo cancellare tutti i suoi multipli, dobbiamo risolvere questa equazione:».

Mm + k_i = pn.

«Fammi capire…».

«A destra dell'uguale, al variare di n, ottieni tutti i multipli di p».

«E fin qua ci siamo».

«A sinistra invece hai tutti i numeri che sono uguali a k_i modulo M. Cioè tutti i numeri non evidenziati di giallo nella ruota».

«Ah, ora ci sono: prima ho tutti i k_i, poi tutti i 30+k_i, eccetera».

«Sì: in pratica m è un contagiri».

«Perfetto, ci sono. Dicevi che dobbiamo risolvere l'equazione?».

«Sì, dobbiamo trovare il modo di utilizzare solo i multipli di p che cadono sulle zone non gialle della ruota».

«E come si fa?».

«Per prima cosa si riscrive l'equazione così: Mm = -k_i mod p».

«Fin qua ci sono».

«Poi si calcola M^-1 mod p».

«Mh. Per esempio? Come sarebbe 30^-1 mod 7?».

«Sarebbe 4, prova a verificare».

«Dunque, 4 moltiplicato 30 fa 120, che diviso per 7 fa 17 con resto di 1. Giusto!».

«Esiste un metodo generale per calcolare questo M^-1, quindi non ci sono problemi. Una volta trovato questo valore, si calcolano questi altri numeri:».

m_i = M^-1(-k_i) mod p

«E cosa ce ne facciamo?».

«Ci servono per calcolare finalmente m, che risulta uguale a pj + m_i».

«Ho capito. Anche se mi piaceva di più l'idea originale».

«Quella è certamente più semplice e immediata da capire, queste che abbiamo visto sono piccole migliorie che velocizzano un po' i conti, al prezzo di una meno immediata comprensibilità».

«E si può fare di meglio?».

«In che senso? Vuoi sapere se esistono algoritmi più veloci?».

«Sì».

«Esistono, ma per capire come funzionano dovremo fare un lungo passo verso l'alto».

«Eh?».

«Ci sarà da astrarre un po', pur cercando di continuare a capire quello che succede».

«Mh, prevedo complicazioni».

«Complicazioni che ci porteranno a scorgere una piccola parte di ciò che genera le ombre che di solito osserviamo».

Il teorema di Gödel senza parole

P(z) è una formula che parla di formule utilizzando numeri.

P(G(P(z))) è una formula che parla della formula che corrisponde a G(P(z)), cioè sé stessa. Affermando di essere indimostrabile. Quindi vera.

Le altre parole sono qua.

Sigma

In attesa del seminario del 13 dicembre, che dovrebbe dirci qualcosa di più sul bosone di Higgs, eminenti fisici ci hanno spiegato come interpretare i risultati. Sia Amedeo Balbi che Peppe Liberti hanno parlato di significatività statistica, e Marco Delmastro ha promesso che cercherà di commentare in diretta i risultati (connessione permettendo).

Il numerino da controllare, quando arriverà la comunicazione ufficiale, sarà il famoso (per chi ha letto gli articoli linkati qua sopra) numero di sigma. Dice la teoria che il valore vero ha circa il 68% di probabilità di essere compreso  in un intervallo di più o meno un sigma attorno alla media dei dati. La domanda è: perché proprio il 68%? Da dove salta fuori questo numero?

Tutto nasce dai cosiddetti teoremi del limite centrale: essi dicono che la somma di un grande numero di variabili casuali ha una distribuzione ben nota, detta appunto normale, o standard. Questo significa, in pratica, che le misure effettuate potranno essere affette da errori accidentali, ma tutti questi errori riescono, in un certo senso, a compensarsi un po'.

Facciamo un esempio: il lancio di un dado.

Il risultato ottenuto lanciando un dado (a 6 facce) è una variabile casuale: se il dado non è truccato io non posso prevedere quale numero uscirà. Ma se lo lancio tante volte, so che le sue facce si presenteranno tutte con una probabilità pari a 1/6. Questo in teoria, perché il dado non ha memoria dei lanci precedenti e, quindi, non rispetterà alla lettera questa regola.

Se io lancio molte volte un dado, e faccio il rapporto tra il numero di volte in cui è uscito un certo numero (diciamo il numero 1) e il numero di lanci totali, mi aspetto che all'aumentare del numero dei lanci questo rapporto si avvicini al valore teorico di 1/6. Più lanci faccio, migliore sarà questa approssimazione.

Ecco un primo esperimento: un dado viene lanciato 1000 volte, e viene calcolato il rapporto tra numero di volte in cui è uscito 1 e numero di lanci totali (cioè 1000). Questa prova è stata ripetuta per mille volte (l'ha fatto il computer, eh), e i mille risultati sono stati rappresentati su questo grafico:

Come si può vedere, i valori si accumulano intorno al valore teorico di 1/6, cioè 1.(6). L'istogramma sembra avere una forma abbastanza regolare, ma siamo ancora molto lontani dalla curva teorica.

In questo secondo esperimento il dado viene lanciato 10000 volte. Ancora una volta la prova è stata ripetuta per mille volte, ed ecco il nuovo grafico:

I dati sono distribuiti in un intervallo più stretto, e la forma appare più regolare.

Un ultimo esperimento: 20000 lanci, e ancora mille ripetizioni. Ecco il grafico:

Leggermente più stretto del precedente, e ancora più regolare.

Ecco un altro grafico in cui i tre precedenti sono rappresentati contemporaneamente, per poterne apprezzare le differenze:

La teoria ci dice che la curva a cui questi istogrammi cercano di assomigliare, detta curva gaussiana, ha la seguente forma base: y = e^-x2. Ed ecco il suo grafico:

Il valore di sigma ha un significato geometrico: è l'ascissa del punto di flesso di destra (mentre sigma cambiato di segno è naturalmente l'ascissa del punto di flesso di sinistra). Dunque un valore compreso in un intervallo di ampiezza sigma attorno al valore medio si trova nella zona evidenziata da questo grafico:

Conoscere la probabilità di essere nella zona delimitata dalle due rette rosse significa conoscere il rapporto tra l'area della curva compresa nella suddetta zona e l'area totale. Questo non è un numero facile da calcolare, perché per calcolare le aree ci servirebbero gli integrali, ma l'integrale della gaussiana è difficilmente trattabile. Riusciamo a calcolare in maniera esatta soltanto l'area compresa sotto tutta la curva (che, in teoria, si estende all'infinito sia a destra che a sinistra), ma non riusciamo a calcolare l'area di una sua generica parte.

E allora ci affidiamo al computer, che ci dice che l'area che stiamo cercando è il 68.3%. Se allarghiamo la zona rossa, andando da -2σ a +2σ, otteniamo un'area pari a circa il 95.5% del totale. Con 3σ siamo al 99.7%. Ed ecco fatto.

Dimenticavo un'ultima cosa: l'area totale compresa dalla gaussiana e l'asse delle ascisse è uguale alla radice quadrata di pi greco, questo per confermare la prezzemolosità del nostro amico π.

[Edit: Marco Delmastro ha iniziato a parlare di statistica, e lo fa lanciando dei dadi. Dategli un'occhiata…]

Come il prezzemolo

«Se ti dico pi greco (o pi greca, come fanno gli snob), a cosa pensi?».

«A una circonferenza».

«Bene. È affascinante scoprire che π non salta fuori solo quando si parla di circonferenze».

«Per esempio?».

«Per esempio, può essere nascosto anche in domande innocenti riguardanti la probabilità, che mai farebbero pensare alle circonferenze».

«E cioè?».

«E cioè: qual è la probabilità che due numeri interi scelti a caso siano primi tra loro?».

«Boh?».

«Partiamo da un esempio finito. Consideriamo i numeri da 1 a 30».

«Bene».

«Quanti sono i numeri primi tra loro?».

«Non lo so, dobbiamo contarli?».

«Sì, in modo da ricavare una regola. Cominciamo osservando che 30 è uguale al prodotto di 2 per 3 per 5».

«Vero».

«Allora, costruiamo una matrice in cui inseriamo, nella riga i e nella colonna j, il Massimo Comun Divisore tra i e j, dove i e j sono numeri che variano da 1 fino a 30».

«Uhm, non so se ho capito bene».

«Ecco qua la matrice:».

«Che brutta».

«Eh, porta pazienza. Allora, quanti elementi contiene?».

«900».

«Bene. Quanti sono quelli multipli di 2?».

«Mh, direi tutti quelli per cui sia i che j sono numeri pari».

«Esatto. Dato che i e j rappresentano anche le righe e le colonne della matrice, possiamo dire che sono tutti i numeri che si trovano in una riga e in una colonna di indice pari».

«Ok. Ma allora possiamo dire che sono un quarto di tutti i numeri, perché gli elementi che stanno su una riga e una colonna pari sono un quarto del totale degli elementi».

«Esatto. Ci restano allora da esaminare 900(1-1/4) elementi».

«Cioè 675».

«Ora, quanti sono, tra questi 675, quelli che sono multipli di 3?».

«Uh, comincia a diventare difficile. Vediamo, sono i numeri che si trovano su una riga multipla di tre e anche su una colonna multipla di tre».

«Sì, vedi che non è difficile?».

«Ma non capisco come fare quando trovo sia numeri multipli di 2 che multipli di 3. Per esempio, quando arrivo a MCD(6,12), cosa succede?».

«Ricordati che i multipli di 2 li abbiamo eliminati, non dobbiamo più considerarli. Stiamo adesso analizzando i 675 numeri rimasti, quindi è come se avessimo tolto le posizioni in cui ci sono i multipli di 2».

«Ah, giusto. Allora mi pare che i multipli di 3 siano 1/9 del totale».

«Perché?».

«Perché si trovano in una posizione ogni 3 di una colonna ogni 3 (o di una riga ogni 3)».

«Perfetto. Quindi se eliminiamo anche questi multipli rimaniamo con 900(1-1/4)(1-1/9) = 600 numeri».

«Bene. Ora guardiamo i multipli di 5?».

«Ci sarebbero prima i multipli di 4, ma quelli sono già andati via quando abbiamo tolto i multipli di 2».

«Giusto».

«Allora, dei 600 numeri rimasti, quanti sono quelli multipli di 5?».

«Uno ogni 5 una riga ogni 5 (o una colonna ogni 5)».

«Quindi ci rimangono 900(1-1/4)(1-1/9)(1-1/25) = 576 numeri».

«E allora?».

«Allora nella matrice abbiamo 576 numeri uguali a 1 oppure coprimi con 2, 3 e 5».

«Giusto».

«Adesso generalizziamo, e passiamo a una matrice infinita».

«Uhm».

«Immaginiamo di non fermarci a n = 30, ma vediamo che succede quando n diventa sempre più grande».

«Potremo continuare a eliminare multipli finché vogliamo».

«Certo, secondo una legge che abbiamo intuito».

«Sarebbe questa: n(1-1/4)(1-1/9)(1-1/25)…».

«Sì. Ricordati che i denominatori di quelle frazioni sono i quadrati dei numeri primi, quindi dopo la parentesi (1-1/25) avrai (1-1/49)».

«Ok».

«Allora, quando n diventa sempre più grande, il rapporto tra i valori uguali a 1 nella matrice e il totale dei valori diventerà sempre più vicino a questa espressione:».

«Dove p_i è un numero primo».

«Esatto. Adesso consideriamo un fattore generico di questo prodotto».

«Una delle tante parentesi del tipo:».

«Esatto. Fai il reciproco».

«Vediamo, prima faccio il denominatore comune, poi capovolgo. Ecco:».

«Benissimo. Se io divido numeratore e denominatore per il quadrato di p_i, ottengo:».

«Che orrore! Perché l'hai scritto così?».

«Non ti ricorda niente?».

«Ah! Ma è il risultato della serie geometrica!».

«Proprio quello. Quindi ognuno di quei fattori può essere scritto come serie geometrica, in questo modo:».

«Mamma mia che roba. Abbiamo trasformato un prodotto di infinite parentesi in un prodotto di infinite serie geometriche».

«Nel reciproco di un prodotto di infinite serie geometriche. E adesso lo calcoliamo».

«Ma dai…».

«Dico davvero. Se applichiamo a quel prodotto la proprietà distributiva…».

«Ma si può?».

«No».

«E allora?».

«E allora facciamo finta che si possa. I Veri Matematici hanno dimostrato che tutti questi passaggi hanno senso, e allora noi ci fidiamo e vediamo di intuire dove si va a finire, lasciando a loro i tediosi calcoli intermedi».

«Mi piace questo metodo».

«Quindi, attenzione: se svolgiamo tutti quei prodotti tra le varie serie geometriche, cosa otteniamo?».

«Un sacco di roba».

«Cominciamo: certamente otteniamo 1».

«Ok, il prodotto di tutti gli 1 che sono al primo posto nelle parentesi».

«Poi otteniamo delle frazioni del tipo 1/p², per ogni numero primo p».

«Giusto».

«Poi frazioni del tipo 1/p⁴, 1/p⁶, eccetera».

«Ho capito: andando avanti le frazioni si complicano, e al denominatore potrò avere tutte le possibili combinazioni dei quadrati dei numeri primi».

«Esatto, ma non solo quadrati: qualunque potenza di quei quadrati».

«Perfetto, ci sono».

«E quindi, prima o poi ogni numero naturale comparirà, elevato al quadrato, al denominatore».

«Sicuramente, ogni numero naturale è scomponibile in fattori primi. Quindi prima o poi compariranno tutti: ho capito».

«Benissimo. Allora ti riordino i risultati che troveremo:».

«Ma no! Quella inutile formula che mi hai spiegato qualche giorno fa».

«VUOI SMETTERLA?».

«Scusa».

«Quanto risultava, quella importantissima formula?».

«Eh, risultava π²/6».

«E allora, riassumendo, la probabilità che in quella matrice ci siano degli 1 è il reciproco di questo numero».

«Quindi la probabilità che due numeri scelti a caso siano primi tra loro è 6/π². Incredibile».

«Davvero incredibile. Per arrivare al risultato siamo passati attraverso i numeri primi, la serie di Taylor del seno, la serie geometrica, gli infiniti, la funzione zeta di Eulero».

«E abbiamo trovato pi greco».

Senso fisico un po' scarsino

«Ehi, cosa stai facendo con quella valvola del termosifone?».

«Eh, prof, la sto riattaccando!».

«Ma perché la staccate?».

«Prof, stamattina quando siamo entrati c'era freddissimo, e allora l'abbiamo staccata per scaldare un po'».

«Scusate, ma sono valvole elettriche, c'è l'impianto che regola la temperatura».

«Ma stamattina c'era troppo freddo, ho staccato la valvola e in un secondo il termo è diventato caldissimo. L'impianto fa schifo».

«E adesso c'è troppo caldo».

«Infatti, sto riattaccando la valvola così si raffredda un po'».

(passano cinque secondi)

«Prof, ma non diventa freddo, come mai?».

«Scusa, e tu pensi che un termo lungo due metri diventi freddo in cinque secondi?».

«Oh, prof, stamattina appena ho staccato la valvola e ha iniziato a girare l'acqua, si è scaldato in un attimo. Non capisco perché adesso fa così».

«Scusa ma, adesso, dato che è stata chiusa la valvola, cosa dovrebbe succedere?».

«Mh. Non passa acqua fredda, vero?».

«Se la valvola chiude, tu cosa dici?».

«Allora forse devo aspettare che si raffreddi?».




Istituto tecnico. Industriale. Classe quinta.

La serie geometrica

«Qual è la frazione generatrice di un numero decimale periodico?».

«Eeh?».

«A cosa è uguale zero virgola tre periodico?».

«A un terzo».

«Perché?».

«Perché sì, è vero!».

«Ottimo esempio di dimostrazione…».

«È vero o no che 1/3 è uguale a 0.(3)?».

«Certo, ma volevo sapere se sai cosa c'è sotto».

«Veramente no».

«C'è una formuletta interessante, che riguarda la serie geometrica».

«Uhm».

«La serie geometrica è questa cosina qui:».

«Una somma infinita. Ha senso?».

«A volte sì».

«Come, a volte? Come è possibile?».

«Cominciamo dal caso finito: se n è un numero naturale, quella somma diventa uguale a:».

1 + q + q² + q³ + … + qⁿ.

«Ok».

«Ora troviamo una espressione più semplice».

«Non va bene quella?».

«Non tanto: ci danno molto fastidio i puntini».

«E perché?».

«Perché se vogliamo capire cosa succede quando n diventa sempre più grande, quella somma diventa una espressione infinitamente lunga, e non sappiamo come gestirla».

«Quindi tu vorresti eliminare i puntini? Si può?».

«Sì. Alle superiori dovrebbero averti insegnato come si fanno le divisioni tra polinomi. Io confido nel fatto che tu le sappia ancora fare…».

«Ehm».

«Grazie alla regola della divisione tra polinomi, puoi verificare tu stesso questa uguaglianza:».

«Mh».

«Altrimenti ti fidi».

«Mi fido sulla parola senza problemi».

«Vabbé. Allora, vedi che la seconda espressione è più semplice della prima, anche se contiene una divisione».

«Sì, se ti danno tanto fastidio i puntini, la seconda espressione non ne ha».

«Prova allora a pensare a cosa succede man mano che n diventa sempre più grande».

«Quel numeratore diventerà sempre più grande, dato che è elevato alla n+1».

«Siamo sicuri?».

«Certo, se elevo un numero a potenza questo aumenta».

«Prova a elevare un mezzo».

«Un quarto. Oops. Ehm».

«Fai una osservazione intelligente».

«Se elevo alla n un numero maggiore di 1, allora ottengo un risultato maggiore del numero di partenza. Altrimenti il risultato è minore».

«Prova a prendere -2, che è sicuramente minore di 1».

«Risulta 4. Uffa. Allora: se elevo alla n un numero maggiore di 1 oppure minore di -1, ottengo un risultato maggiore, altrimenti è minore».

«Calcola -2 elevato alla 3».

«Fa -8, argh, è minore. Ma quanti casi ci sono?».

«Se vuoi semplificare un po' il numero di casi, devi usare il valore assoluto. Se elevi alla n un numero in valore assoluto maggiore di 1, ottieni un numero che, in valore assoluto, è maggiore. Se elevi invece alla n un numero in valore assoluto minore di 1, allora ottieni un numero che, sempre in valore assoluto, è minore di quello di partenza».

«Ho capito. Mi pare che tu abbia lasciato fuori 1 e -1».

«Sì, è vero. Se q = 1, la formula che ti ho scritto prima non vale».

«Perché?».

«Perché al denominatore risulterebbe zero».

«Ah, già. E allora?».

«Allora non la usiamo, ma non è difficile capire come stanno le cose. Se q = 1, la somma delle potenze di q diventa semplicemente una somma di tanti 1».

«Che aumenta sempre».

«Infatti. Se invece q = -1 la formula è valida, e il numeratore di quella frazione diventa alternativamente uguale a 0 oppure a -2».

«Una schifezza».

«Sì. Noi siamo interessati al caso di q minore di 1 in valore assoluto».

«Perché proprio quello?».

«Perché in quel caso, quando n diventa infinitamente grande, la potenza qⁿ⁺¹ diventa infinitamente piccola».

«E allora possiamo trascurarla, quando facciamo i calcoli?».

«Esatto. I Veri Matematici parlano di limite, c'è tutta una teoria sotto che motiva in modo preciso i vari passaggi, ma a noi interessa avere intuito il risultato».

«Che sarebbe questo?».

«Esatto. Quando q è, in valore assoluto, minore di 1, si dice che la serie geometrica converge, e il risultato viene chiamato somma della serie. Mentre q viene detto ragione della serie».

«Bello».

«E ora puoi calcolare quanto vale 0.(3)».

«Con la serie?».

«Sì».

«E come faccio?».

«Cosa significa zero virgola tre periodico?».

«Che ci sono infiniti 3 dopo la virgola».

«Che significato ha il primo di quei 3?».

«Uhm, boh, 3 decimi?».

«Esatto. E il secondo?».

«3 centesimi».

«E così via. Puoi quindi scrivere 0.(3) come una somma di tante frazioni:».

3/10 + 3/100 + 3/1000 + …

«Una serie geometrica?».

«Esatto».

«Ma non capisco quanto vale q».

«Te la scrivo in un altro modo:».

3/10 (1 + 1/10 + 1/100 + …).

«Ah, ho capito! La somma tra parentesi è la serie geometrica!».

«Di ragione?».

«Di ragione 1/10».

«Che è minore di 1, in valore assoluto. Quindi?».

«Quindi converge».

«A quale valore?».

«A 1/(1-1/10)».

«Cioè 1/(9/10), che è uguale a 10/9».

«E se adesso la moltiplico per il coefficiente 3/10, ottengo proprio 3/9, cioè 1/3. È la regolina che mi avevano insegnato alle medie per trovare la frazione generatrice di un numero decimale periodico, ora mi ricordo».

«Ottimo».

«Finalmente qualcosa di utile!».

«ALLORA?».

Il professor Apotema insegna: il calcolo delle differenze e il calcolo differenziale

Avevo già parlato dell'approccio assiomatico ai numeri iperreali e di come alcuni (pochi) insegnanti lo usino per spiegare l'analisi matematica.

Qualche giorno fa alcuni di questi insegnanti si sono ritrovati a Venezia, al liceo Foscarini, per una giornata di studio e confronto sull'analisi infinitesimale; tra questi c'era anche Giorgio Goldoni, in arte professor Apotema, di cui ho già recensito il primo libro su questo argomento.

Come aveva promesso ha continuato a scrivere e, dopo il volume in cui presenta i numeri iperreali, ora ne ha concluso uno nuovo, dedicato al calcolo delle differenze e al calcolo differenziale.

In 425 pagine vengono presentati, utilizzando l'approccio iperreale, argomenti molto noti, come le derivate, lo studio di funzione e i problemi di massimo e minimo, e anche argomenti poco noti (io, almeno, non li conoscevo), come il calcolo delle differenze, che sarebbe l'analogo discreto del calcolo differenziale. Esistono, ad esempio, formule sulle differenze discrete analoghe a quelle sulle derivate, esiste una versione discreta delle regole di de l'Hôpital, ed esiste persino una versione discreta del polinomio di Taylor, detto polinomio di Gregory-Newton. Il tutto è sempre presentato sotto forma di dialogo tra il professor Apotema e i suoi studenti.

Insomma, anche questo è un testo consigliatissimo.

Giorgio Goldoni, Il professor Apotema insegna: il calcolo delle differenze e il calcolo differenziale, ilmiolibro.it, 20€.

Le magie di Eulero

Prendiamo la funzione y = sin(x): bellina da disegnare, ma difficile da trattare. Va bene, pazienza, Taylor ha trovato una formula che permette di trasformare le funzioni difficili in polinomi. E allora possiamo scrivere che:

sin(x) = x - x³/3! + x⁵/5! - x⁷/7! + …

«Bé, non è proprio un polinomio questo, eh. Si deve andare avanti all'infinito, non ci si può fermare».

«Lo so, ma Eulero vedeva molto lontano, e ai tempi l'infinito veniva gestito in modo molto sportivo».

«Andiamo bene. E cosa ha combinato, Eulero?».

«Per prima cosa ha calcolato il polinomio…».

«…infinito…».

«…infinito, va bene, di sin(x)/x».

«Basta dividere per x, no?».

«Sì, e si ottiene questo:».

P(x) = sin(x)/x = 1 - x²/3! + x⁴/5! - x⁶/7! + …

«Questo era facile».

«Ora calcoliamo le radici di questo polinomio».

«Eh?».

«Vediamo in quali punti si annulla».

«Immagino che si annullerà quando è nullo il seno: in infiniti punti».

«Naturalmente. Quali sono?».

«Uhm, vediamo, π, 2π, 3π, …».

«Non dimenticare i valori negativi!».

«Ah, già, ci sono anche -π, -2π, eccetera. E anche lo zero».

«Eh, no, lo zero no».

«Perché?».

«Perché il dominio di sin(x)/x esclude lo zero, quello lo lasciamo fuori».

«Ah, giusto».

«Ora, un polinomio di qualsiasi grado può essere scomposto nel prodotto di tanti binomi del tipo (x-r_i), dove gli r_i sono le sue radici, moltiplicato per il coefficiente del termine di grado massimo».

«È vero, ma qui non c'è un grado massimo!».

«Infatti. Allora giriamo il problema, partiamo dal termine noto. Questo è, ehm, noto».

«Già, è uguale a 1».

«Allora esprimiamo questo polinomio come prodotto di tanti binomi del tipo (1-x/r_i)».

«Uhm, fammi pensare… Certamente se svolgo i calcoli mi risulta un termine noto uguale a 1, ma non capisco bene il significato di quei binomi».

«Guarda bene: ognuno di loro si annulla se sostituisco al posto di x la radice r_i».

«Ah, è vero. Quindi questo è un modo equivalente di scomporre, ho capito».

«Ottimo. Quindi il nostro P(x) è diventato questa espressione:».

P(x) = (1-x/r₁)(1-x/r₂)(1-x/r₃)…

«Un prodotto infinito».

«Esatto. Ora ti ordino i vari valori di r_i in modo da fare saltare fuori qualche prodotto notevole».

«Uh, quelli che si studiavano in prima superiore».

«Proprio loro. In particolare, userò la differenza tra due quadrati».

«Me la ricordo! Dice che (a+b)(a-b) è uguale a a²-b²».

«Perfetto. Guarda allora questa espressione di P(x) e prova a trasformarla:».

P(x) = (1-x/π)(1+x/π)(1-x/(2π))(1+x/(2π))…

«Ah, ho capito. A due a due le parentesi si moltiplicano, e ottengo questo:».

P(x) = (1-x²/π²)(1-x²/(2π)²)(1-x²/(3π)²)…

«Benissimo. Ora calcoliamo il prodotto».

«Eh? Stai scherzando? Come si fa? È infinito!».

«Sì, hai ragione. Calcoliamoci solo il termine di secondo grado».

«E come facciamo?».

«Osserva che in ogni parentesi compare una x di secondo grado…».

«E quindi i termini di secondo grado si hanno solo quando prendo una delle x e la moltiplico per tutti gli 1 che compaiono nelle altre parentesi!».

«Esatto, altrimenti ottieni gradi più alti».

«Allora forse ce la faccio a fare il calcolo, vediamo: dalla prima parentesi ottengo 1/π²…».

«Attenzione al segno!».

«Vero, sono tutti termini negativi. Allora, raccolgo un segno meno e non ci penso più: quindi, a parte il segno, ottengo questi numeri».

1/π², 1/(2π²), 1/(3π²), …

«Bene. Questi numeri sono tutti sommati tra di loro, vero?».

«Certo, l'espressione finale che ottengo è questa:».

- 1/π² - 1/(2π²) - 1/(3π²) - …

«Che ti scriverò in questo modo:».

«Eh? Cos'è quella lettera?».

«Si chiama funzione zeta di Riemann, ζ è la lettera greca zeta».

«Quella dell'ipotesi di Riemann?».

«Proprio lei».

«E allora? Cosa abbiamo ottenuto?».

«Abbiamo calcolato il valore di -ζ(2)/π²».

«Davvero? E come abbiamo fatto? Non vedo il risultato, ma solo una lunga (e discutibile) trasformazione».

«Eh, ma guarda l'inizio della trasformazione: non dimenticarti il punto di partenza».

«Ti riferisci a P(x)? Cioè a sin(x)/x?».

«Certamente. Qual è il coefficiente del termine di secondo grado, nella prima espressione di P(x)?».

«È -1/3!, cioè -1/6».

«Perfetto, allora -ζ(2)/π² = -1/6, quindi ζ(2) = π²/6».

«Uhm, vabbé, carino, ma non ho capito a cosa ci ser…».

«COSA?».

«Ehm, no, mi chiedevo l'util…».

«TU NON STAI PENSANDO DA VERO MATEMATICO!».

«Uh, ecco, non volevo…».

«TI SEMBRANO DOMANDE DA FARE?».

«Mi dispiace…».

«SARÀ MEGLIO!».