sin(x) = x - x3/3! + x5/5! - x7/7! + …
«Bé, non è proprio un polinomio questo, eh. Si deve andare avanti all'infinito, non ci si può fermare».
«Lo so, ma Eulero vedeva molto lontano, e ai tempi l'infinito veniva gestito in modo molto sportivo».
«Andiamo bene. E cosa ha combinato, Eulero?».
«Per prima cosa ha calcolato il polinomio…».
«…infinito…».
«…infinito, va bene, di sin(x)/x».
«Basta dividere per x, no?».
«Sì, e si ottiene questo:».
P(x) = sin(x)/x = 1 - x2/3! + x4/5! - x6/7! + …
«Questo era facile».
«Ora calcoliamo le radici di questo polinomio».
«Eh?».
«Vediamo in quali punti si annulla».
«Immagino che si annullerà quando è nullo il seno: in infiniti punti».
«Naturalmente. Quali sono?».
«Uhm, vediamo, π, 2π, 3π, …».
«Non dimenticare i valori negativi!».
«Ah, già, ci sono anche -π, -2π, eccetera. E anche lo zero».
«Eh, no, lo zero no».
«Perché?».
«Perché il dominio di sin(x)/x esclude lo zero, quello lo lasciamo fuori».
«Ah, giusto».
«Ora, un polinomio di qualsiasi grado può essere scomposto nel prodotto di tanti binomi del tipo (x-ri), dove gli ri sono le sue radici, moltiplicato per il coefficiente del termine di grado massimo».
«È vero, ma qui non c'è un grado massimo!».
«Infatti. Allora giriamo il problema, partiamo dal termine noto. Questo è, ehm, noto».
«Già, è uguale a 1».
«Allora esprimiamo questo polinomio come prodotto di tanti binomi del tipo (1-x/ri)».
«Uhm, fammi pensare… Certamente se svolgo i calcoli mi risulta un termine noto uguale a 1, ma non capisco bene il significato di quei binomi».
«Guarda bene: ognuno di loro si annulla se sostituisco al posto di x la radice ri».
«Ah, è vero. Quindi questo è un modo equivalente di scomporre, ho capito».
«Ottimo. Quindi il nostro P(x) è diventato questa espressione:».
P(x) = (1-x/r1)(1-x/r2)(1-x/r3)…
«Un prodotto infinito».
«Esatto. Ora ti ordino i vari valori di ri in modo da fare saltare fuori qualche prodotto notevole».
«Uh, quelli che si studiavano in prima superiore».
«Proprio loro. In particolare, userò la differenza tra due quadrati».
«Me la ricordo! Dice che (a+b)(a-b) è uguale a a2-b2».
«Perfetto. Guarda allora questa espressione di P(x) e prova a trasformarla:».
P(x) = (1-x/π)(1+x/π)(1-x/(2π))(1+x/(2π))…
«Ah, ho capito. A due a due le parentesi si moltiplicano, e ottengo questo:».
P(x) = (1-x2/π2)(1-x2/(2π)2)(1-x2/(3π)2)…
«Benissimo. Ora calcoliamo il prodotto».
«Eh? Stai scherzando? Come si fa? È infinito!».
«Sì, hai ragione. Calcoliamoci solo il termine di secondo grado».
«E come facciamo?».
«Osserva che in ogni parentesi compare una x di secondo grado…».
«E quindi i termini di secondo grado si hanno solo quando prendo una delle x e la moltiplico per tutti gli 1 che compaiono nelle altre parentesi!».
«Esatto, altrimenti ottieni gradi più alti».
«Allora forse ce la faccio a fare il calcolo, vediamo: dalla prima parentesi ottengo 1/π2…».
«Attenzione al segno!».
«Vero, sono tutti termini negativi. Allora, raccolgo un segno meno e non ci penso più: quindi, a parte il segno, ottengo questi numeri».
1/π2, 1/(2π2), 1/(3π2), …
«Bene. Questi numeri sono tutti sommati tra di loro, vero?».
«Certo, l'espressione finale che ottengo è questa:».
- 1/π2 - 1/(2π2) - 1/(3π2) - …
«Che ti scriverò in questo modo:».
«Eh? Cos'è quella lettera?».
«Si chiama funzione zeta di Riemann, ζ è la lettera greca zeta».
«Quella dell'ipotesi di Riemann?».
«Proprio lei».
«E allora? Cosa abbiamo ottenuto?».
«Abbiamo calcolato il valore di -ζ(2)/π2».
«Davvero? E come abbiamo fatto? Non vedo il risultato, ma solo una lunga (e discutibile) trasformazione».
«Eh, ma guarda l'inizio della trasformazione: non dimenticarti il punto di partenza».
«Ti riferisci a P(x)? Cioè a sin(x)/x?».
«Certamente. Qual è il coefficiente del termine di secondo grado, nella prima espressione di P(x)?».
«È -1/3!, cioè -1/6».
«Perfetto, allora -ζ(2)/π2 = -1/6, quindi ζ(2) = π2/6».
«Uhm, vabbé, carino, ma non ho capito a cosa ci ser…».
«COSA?».
«Ehm, no, mi chiedevo l'util…».
«TU NON STAI PENSANDO DA VERO MATEMATICO!».
«Uh, ecco, non volevo…».
«TI SEMBRANO DOMANDE DA FARE?».
«Mi dispiace…».
«SARÀ MEGLIO!».
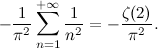
1 commento:
wow
Posta un commento