«A una circonferenza».
«Bene. È affascinante scoprire che π non salta fuori solo quando si parla di circonferenze».
«Per esempio?».
«Per esempio, può essere nascosto anche in domande innocenti riguardanti la probabilità, che mai farebbero pensare alle circonferenze».
«E cioè?».
«E cioè: qual è la probabilità che due numeri interi scelti a caso siano primi tra loro?».
«Boh?».
«Partiamo da un esempio finito. Consideriamo i numeri da 1 a 30».
«Quanti sono i numeri primi tra loro?».
«Non lo so, dobbiamo contarli?».
«Sì, in modo da ricavare una regola. Cominciamo osservando che 30 è uguale al prodotto di 2 per 3 per 5».
«Vero».
«Allora, costruiamo una matrice in cui inseriamo, nella riga i e nella colonna j, il Massimo Comun Divisore tra i e j, dove i e j sono numeri che variano da 1 fino a 30».
«Uhm, non so se ho capito bene».
«Ecco qua la matrice:».
«Che brutta».
«Eh, porta pazienza. Allora, quanti elementi contiene?».
«900».
«Bene. Quanti sono quelli multipli di 2?».
«Mh, direi tutti quelli per cui sia i che j sono numeri pari».
«Esatto. Dato che i e j rappresentano anche le righe e le colonne della matrice, possiamo dire che sono tutti i numeri che si trovano in una riga e in una colonna di indice pari».
«Ok. Ma allora possiamo dire che sono un quarto di tutti i numeri, perché gli elementi che stanno su una riga e una colonna pari sono un quarto del totale degli elementi».
«Esatto. Ci restano allora da esaminare 900(1-1/4) elementi».
«Cioè 675».
«Ora, quanti sono, tra questi 675, quelli che sono multipli di 3?».
«Uh, comincia a diventare difficile. Vediamo, sono i numeri che si trovano su una riga multipla di tre e anche su una colonna multipla di tre».
«Sì, vedi che non è difficile?».
«Ma non capisco come fare quando trovo sia numeri multipli di 2 che multipli di 3. Per esempio, quando arrivo a MCD(6,12), cosa succede?».
«Ricordati che i multipli di 2 li abbiamo eliminati, non dobbiamo più considerarli. Stiamo adesso analizzando i 675 numeri rimasti, quindi è come se avessimo tolto le posizioni in cui ci sono i multipli di 2».
«Ah, giusto. Allora mi pare che i multipli di 3 siano 1/9 del totale».
«Perché?».
«Perché si trovano in una posizione ogni 3 di una colonna ogni 3 (o di una riga ogni 3)».
«Perfetto. Quindi se eliminiamo anche questi multipli rimaniamo con 900(1-1/4)(1-1/9) = 600 numeri».
«Bene. Ora guardiamo i multipli di 5?».
«Ci sarebbero prima i multipli di 4, ma quelli sono già andati via quando abbiamo tolto i multipli di 2».
«Giusto».
«Allora, dei 600 numeri rimasti, quanti sono quelli multipli di 5?».
«Uno ogni 5 una riga ogni 5 (o una colonna ogni 5)».
«Quindi ci rimangono 900(1-1/4)(1-1/9)(1-1/25) = 576 numeri».
«E allora?».
«Allora nella matrice abbiamo 576 numeri uguali a 1 oppure coprimi con 2, 3 e 5».
«Giusto».
«Adesso generalizziamo, e passiamo a una matrice infinita».
«Uhm».
«Immaginiamo di non fermarci a n = 30, ma vediamo che succede quando n diventa sempre più grande».
«Potremo continuare a eliminare multipli finché vogliamo».
«Certo, secondo una legge che abbiamo intuito».
«Sarebbe questa: n(1-1/4)(1-1/9)(1-1/25)…».
«Sì. Ricordati che i denominatori di quelle frazioni sono i quadrati dei numeri primi, quindi dopo la parentesi (1-1/25) avrai (1-1/49)».
«Ok».
«Allora, quando n diventa sempre più grande, il rapporto tra i valori uguali a 1 nella matrice e il totale dei valori diventerà sempre più vicino a questa espressione:».
«Dove pi è un numero primo».
«Esatto. Adesso consideriamo un fattore generico di questo prodotto».
«Una delle tante parentesi del tipo:».
«Esatto. Fai il reciproco».
«Vediamo, prima faccio il denominatore comune, poi capovolgo. Ecco:».
«Benissimo. Se io divido numeratore e denominatore per il quadrato di pi, ottengo:».
«Che orrore! Perché l'hai scritto così?».
«Non ti ricorda niente?».
«Ah! Ma è il risultato della serie geometrica!».
«Proprio quello. Quindi ognuno di quei fattori può essere scritto come serie geometrica, in questo modo:».
«Mamma mia che roba. Abbiamo trasformato un prodotto di infinite parentesi in un prodotto di infinite serie geometriche».
«Nel reciproco di un prodotto di infinite serie geometriche. E adesso lo calcoliamo».
«Ma dai…».
«Dico davvero. Se applichiamo a quel prodotto la proprietà distributiva…».
«Ma si può?».
«No».
«E allora?».
«E allora facciamo finta che si possa. I Veri Matematici hanno dimostrato che tutti questi passaggi hanno senso, e allora noi ci fidiamo e vediamo di intuire dove si va a finire, lasciando a loro i tediosi calcoli intermedi».
«Mi piace questo metodo».
«Quindi, attenzione: se svolgiamo tutti quei prodotti tra le varie serie geometriche, cosa otteniamo?».
«Un sacco di roba».
«Cominciamo: certamente otteniamo 1».
«Ok, il prodotto di tutti gli 1 che sono al primo posto nelle parentesi».
«Poi otteniamo delle frazioni del tipo 1/p2, per ogni numero primo p».
«Giusto».
«Poi frazioni del tipo 1/p4, 1/p6, eccetera».
«Ho capito: andando avanti le frazioni si complicano, e al denominatore potrò avere tutte le possibili combinazioni dei quadrati dei numeri primi».
«Esatto, ma non solo quadrati: qualunque potenza di quei quadrati».
«Perfetto, ci sono».
«E quindi, prima o poi ogni numero naturale comparirà, elevato al quadrato, al denominatore».
«Sicuramente, ogni numero naturale è scomponibile in fattori primi. Quindi prima o poi compariranno tutti: ho capito».
«Benissimo. Allora ti riordino i risultati che troveremo:».
«Ma no! Quella inutile formula che mi hai spiegato qualche giorno fa».
«VUOI SMETTERLA?».
«Scusa».
«Quanto risultava, quella importantissima formula?».
«Eh, risultava π2/6».
«E allora, riassumendo, la probabilità che in quella matrice ci siano degli 1 è il reciproco di questo numero».
«Quindi la probabilità che due numeri scelti a caso siano primi tra loro è 6/π2. Incredibile».
«Davvero incredibile. Per arrivare al risultato siamo passati attraverso i numeri primi, la serie di Taylor del seno, la serie geometrica, gli infiniti, la funzione zeta di Eulero».
«E abbiamo trovato pi greco».

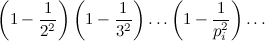

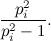
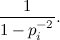
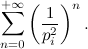
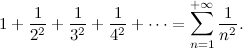
Nessun commento:
Posta un commento