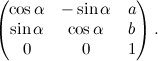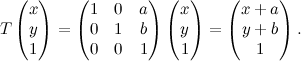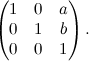Erlangen 1872 — Componiamo

Dopo aver definito le traslazioni e le rotazioni, ci potrebbe venire voglia di combinarle insieme. Che succede se applichiamo una rotazione e una traslazione a un punto (o a una figura)? Possiamo farlo nell'ordine che ci pare? Che trasformazione otteniamo?

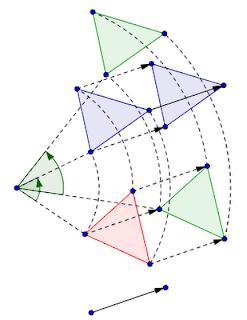
Questa figura (complicata, sì) ci fa capire che la composizione di una rotazione e una traslazione non è commutativa. Proviamo a capire: il percorso con le figure blu ci mostra che la figura rossa viene prima ruotata di un certo angolo, poi traslata secondo un certo vettore. Il percorso con le figure verdi invece ci mostra la figura rossa che prima viene traslata, poi ruotata. Come si vede, i due percorsi non terminano sulla stessa figura: quindi bisogna stare molto attenti all'ordine in cui vengono applicate le trasformazioni.

In realtà, però, non esiste un insieme delle traslazioni+rotazioni, diverso da quello delle rotazioni+traslazioni: la figura qua sotto mostra come sia possibile arrivare alla stessa figura applicando, in un caso, prima una traslazione e poi una rotazione, in un secondo caso invece applicando prima una rotazione e poi una traslazione (diversa dalla precedente, naturalmente).

Quindi esiste un unico gruppo che contiene tutte le possibili composizioni di traslazioni e rotazioni. Questo gruppo, detto delle isometrie dirette (o delle rototraslazioni), contiene i due gruppi di rotazioni e traslazioni (che si dicono essere sottogruppi del gruppo più grande).

La matrice associata a queste trasformazioni è la seguente:

Manca ancora poco per poter parlare della prima geometria.

L'aquila

Erlangen 1872 — Rotazioni

Parliamo di rotazioni intorno all'origine.

Anche la rotazione è una trasformazione del piano, ed è certamente diversa da una traslazione. Cioè: è impossibile, anche utilizzando un numero qualsiasi di traslazioni, ottenere una rotazione. Capire il perché è molto semplice: nella traslazione tutti i punti si spostano, non ce n'è nemmeno uno che rimane fermo. Nella rotazione, invece, esiste un punto che sta fermo: il centro della rotazione. Nel linguaggio delle trasformazioni i punti che rimangono invariati sotto l'azione di una trasformazione si dicono punti uniti.

Quindi le rotazioni non stanno all'interno del gruppo delle traslazioni. A loro volta, però, esse formano un gruppo. Infatti esiste l'elemento neutro, che è la rotazione di un angolo nullo, ed esiste l'inverso: la rotazione nel verso opposto. Si adotta la convenzione di far corrispondere agli angoli positivi le rotazioni in senso antiorario, e agli angoli negativi quella in senso orario. La matrice associata a una rotazione in senso antiorario intorno all'origine di un angolo α è la seguente:

Stiamo sempre utilizzando la notazione utilizzata per le traslazioni, e cioè stiamo (per ora misteriosamente) associando a un punto del piano le coordinate (x,y,1) e non (x,y), come normalmente si fa.

Concludendo: il gruppo delle rotazioni e quello delle traslazioni sono due gruppi diversi. Entrambi danno luogo a due geometrie che, però, sono ancora troppo magre. Dobbiamo ingrassarle ancora un pochino.

Erlangen 1872 — Equazioni

Se noi ci mettiamo sul piano cartesiano, possiamo anche scrivere le equazioni delle trasformazioni geometriche. Per esempio, se si indica il vettore v di una traslazione mediante le sue componenti lungo gli assi cartesiani (e cioè v=(a,b)), allora l'equazione della traslazione di vettore v può essere scritta semplicemente in questo modo:

T(x,y) = (x+a,y+b).

Ora complichiamo le cose semplici. Gli studenti universitari imparano presto che ciò che i professori chiamano geometria è in realtà algebra lineare, almeno per qualche mese. Quella scritta sopra è, in effetti, una trasformazione lineare. Bene, ad ogni trasformazione lineare è associata una matrice, oggetto scomodo e dalle proprietà misteriose. In forma matriciale la semplice equazione scritta sopra diventa così:

Il fatto che il punto di coordinate (x,y) sia diventato (x,y,1) è dovuto a due considerazioni. La prima è che così l'operazione con le matrici funziona, altrimenti non si riuscirebbe a ottenere come risultato (x+a,y+b). La seconda la facciamo più avanti.

Diciamo dunque che la matrice associata alla traslazione di vettore v(a,b) è la seguente:

Quindi lo studio delle proprietà delle traslazioni potrebbe essere fatto analizzando questo tipo di matrici (ma noi non lo facciamo). E anche il gruppo delle traslazioni diventa il gruppo delle matrici di questo tipo, mentre la composizione di traslazioni diventa la moltiplicazione righe per colonne delle matrici.

Ma lasciamo queste cose agli studenti universitari di geometria, e passiamo ad altre trasformazioni.

Teach and Learn

Erlangen 1872 — Traslazioni

Vediamo di applicare quanto abbiamo detto alla geometria. Il nostro insieme è l'insieme dei punti del piano; una trasformazione è una generica macchinetta che prende un punto e gli cambia posizione, seguendo certe regole, naturalmente.

Bene, prendiamo le macchinette-trasformazioni e le mettiamo dentro a un insieme (infinito, naturalmente). Poi definiamo un'operazione su questo insieme, e la chiamiamo composizione. La composizione di due trasformazioni a e b è semplicemente quella trasformazione che si ottiene applicando nell'ordine prima a e poi b. Tutto qua.

L'unica cosa strana è che questa operazione non agisce su numeri, come normalmente ci si aspetta da un'operazione come si deve, ma agisce su trasformazioni geometriche.

Esempio: le traslazioni. Tutti quanti dovrebbero conoscere il termine: una traslazione è una trasformazione del piano che prende tutti i punti e li sposta di una distanza fissa nella medesima direzione.

La figura rossa viene trasformata in quella blu (il che significa che ogni punto della figura viene trasformato, naturalmente). Non è che gli altri punti siano fermi, beninteso. La traslazione agisce su tutti i punti del piano: noi ne abbiamo evidenziati alcuni, formanti una figura, e abbiamo analizzato cosa è successo a quelli.

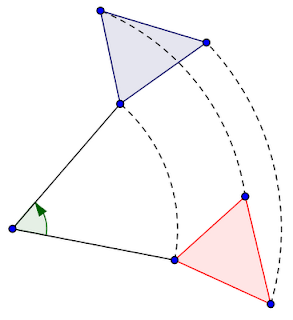
Primo fatto: sulle traslazioni è possibile effettuare una operazione, quella che abbiamo chiamato composizione. Comporre due traslazioni significa applicarne prima una e poi l'altra. In questo caso non è importante specificare l'ordine, ma con altri tipi di trasformazioni lo sarà (questo significa che, in generale, la composizione non è una operazione commutativa). Per trovare il risultato della composizione ci basta sommare i due vettori, come abbiamo imparato a fare alle medie (con la regola del parallelogrammo, per esempio).

Ecco, in questa figura si vede la composizione di due traslazioni (indicate con le frecce tratteggiate), che possono essere viste come un'unica traslazione (indicata con la freccia continua). In alto, i due vettori corrispondenti alle due traslazioni vengono sommati con la regola del parallelogrammo, e il risultato è proprio il vettore che congiunge la figura rossa con quella verde, in basso.

Possiamo parlare di gruppo delle traslazioni? Per farlo, dobbiamo verificare che esista l'elemento neutro e che per ogni traslazione esista quella opposta. Allora, l'elemento neutro è la traslazione di vettore nullo, cioè la traslazione che lascia tutto fermo. L'opposto, invece, è quella traslazione che si ottiene girando il vettore: mettendo cioè la punta al posto della coda, e viceversa.

Quindi le traslazioni formano un gruppo. Possiamo già parlare di geometria, secondo Klein? In teoria potremmo, in pratica però questa geometria è un po' troppo povera: bisogna allargare un po' di più l'insieme delle operazioni per poter ritrovare una geometria ben nota.

Erlangen 1872 — Invarianti

Un invariante è semplicemente qualcosa che rimane costante. E fin qua.

Per capire qualcosa di più, dobbiamo tener presente che il concetto di invariante deve essere associato a quello di trasformazione. In pratica: la trasformazione mescola apparentemente gli oggetti di cui disponiamo, ma sotto sotto c'è qualcosa che rimane fisso. Si tratta di scoprirlo, e il gioco è fatto.

Giochino: abbiamo una scacchiera 8×8, e la vogliamo ricoprire con delle tessere del domino, di dimensione 1×2. Siamo capaci? Spero di sì, basta provare: in ogni riga mettiamo quattro tessere e siamo a posto. Bene, ora tagliamo via dalla scacchiera due caselle d'angolo opposte. Siamo ancora in grado di ricoprire la scacchiera con le tessere di prima? Se proviamo, non ci riusciamo. Ma, anche provando per molto tempo, non riusciremmo a verificare tutte le possibili configurazioni di tessere; però possiamo dimostrare l'impossibilità.

Indichiamo con n il numero di caselle nere visibili (cioè non coperte da nessuna tessera del domino), e con b il numero di caselle bianche visibili. Chiamiamo d la differenza n-b. Ora prendiamo la scacchiera completa: essa contiene 32 caselle bianche e 32 caselle nere, quindi d = 0. Che succede ogni volta che posizioniamo una tessera del domino?

Succede che copriamo una casella bianca e una casella nera, quindi sia n che b diminuiscono di 1; però la differenza d non varia, perché (n-1) - (b-1) è uguale a n-b. Quindi comunque noi posizioniamo una tessera del domino, la quantità d rimane costante. Ecco il nostro invariante.

Ora pensiamo alla scacchiera senza due caselle d'angolo. Se ci pensiamo un attimo, ci rendiamo conto del fatto che due caselle d'angolo hanno lo stesso colore: se le togliamo, il numero di caselle bianche sarà diverso da quello di caselle nere (diciamo di aver tolto due caselle bianche: in questo caso n-b = 2 — se togliamo due caselle nere allora n-b = -2). Ecco il motivo per cui è impossibile ricoprire questa scacchiera con le tessere del domino: il posizionamento di una tessera non fa variare d, che rimarrà sempre uguale a 2 (oppure a -2), eppure noi vorremmo arrivare a una situazione in cui tutte le caselle sono state coperte, cioè d = 0. Impossibile.

Gli invarianti sono bellissimi.

Erlangen 1872 — Gruppi

Un gruppo è una struttura algebrica caratterizzata da una operazione binaria associativa, dotata di elemento neutro e per la quale ogni elemento della struttura possiede elemento inverso.

Ecco, già dalla definizione si capisce che quello di gruppo è un concetto un po' più complicato.

Partiamo dall'inizio: struttura algebrica lo possiamo tradurre con mucchio di roba. Non specifichiamo altro: è un insieme di oggetti matematici che servono a qualcosa, il cosa è spiegato in seguito dalle proprietà che devono essere soddisfatte dagli oggetti.

Operazione binaria associativa è abbastanza facile: si tratta di una operazione che prende due elementi del gruppo e ne produce un terzo. Se pensiamo alle normali operazioni che conosciamo, va bene. Dobbiamo però tenere presente che il concetto di gruppo è molto generale, e quindi l'operazione potrebbe non essere una operazione tra numeri. Insomma, il gruppo è un insieme di oggetti, che potrebbero anche non essere numeri, ma sui quali si deve poter operare. L'operazione deve poi essere associativa, cioè deve essere una operazione decente. Se indichiamo l'operazione col generico simbolo ∗, la proprietà associativa è questa:

a∗(b∗c) = (a∗b)∗c.

Un esempio di operazione non associativa? Eccolo qua: la media tra due numeri. Se a∗b è uguale alla media tra a e b (cioè (a+b)/2) allora ci basta un esempio per capire che non gode della proprietà associativa: 1∗(2∗3) = 1∗2.5 = 1.75, mentre (1∗2)∗3 = 1.5∗3 = 2.25.

Elemento neutro è molto semplice: è come 1 per la moltiplicazione o 0 per l'addizione; deve cioè esistere un oggetto, all'interno del gruppo, il quale non produce effetti se inserito nell'operazione. In simboli, se si indica con e l'elemento neutro, questo è tale per cui:

a∗e = e∗a = a.

Arriviamo all'inverso di un elemento. L'inverso di a si indica con -a ed è tale per cui:

a∗(-a) = (-a)∗a = e.

Esempio: se consideriamo la somma di due numeri, abbiamo che l'elemento neutro è lo 0, e l'inverso di a è quel numero, che si indica con -a, tale per cui a + (-a) = 0. Insomma, l'inverso di 3 è -3, quello che normalmente si chiama opposto.

Se invece consideriamo il prodotto di due numeri, in questo caso l'elemento neutro è 1, e l'inverso di a è quel numero, che si indica con 1/a, tale per cui a × (1/a) = 1. Insomma, l'inverso di 3 è 1/3, quello che normalmente si chiama reciproco.

Basta, il gruppo non ha altre proprietà, queste sono quelle di base.

Naturalmente l'astuto lettore avrà notato che se si prendono, ad esempio, i numeri naturali, gli esempi fatti sopra non funzionano: -3 e 1/3 non appartengono all'insieme dei numeri naturali. Quindi quando si definisce un gruppo bisogna specificare bene anche l'insieme che stiamo considerando, e non solo l'operazione. Dunque potremmo dire che l'insieme dei numeri interi, con l'operazione di somma, è un gruppo. Oppure che l'insieme dei numeri razionali senza lo zero, con l'operazione di moltiplicazione, è un gruppo. Insomma, occorre che l'insieme considerato sia chiuso rispetto all'operazione, il che significa che ogni operazione tra due elementi qualsiasi deve dare un risultato che appartiene ancora all'insieme.

Se si è precisi, tutto fila liscio.

Erlangen 1872 — Trasformazioni

Si parlava di studio delle proprietà di uno spazio che sono invarianti rispetto ad un gruppo di trasformazioni. Allora, quando diciamo spazio possiamo intendere anche piano, e questo non perché i matematici non conoscano la differenza tra le due parole, ma perché con spazio si intende un po' tutto. Insomma, quello che la gente normale considera spazio, i matematici lo chiamano spazio a tre dimensioni. E così il piano diventa lo spazio a due dimensioni, la retta lo spazio a una dimensione, e abbiamo spazio (appunto) per generalizzare a quattro, cinque, n dimensioni.

Fermiamoci a due dimensioni, che i disegni sono più facili.

Il piano è fatto di punti, che ora dobbiamo immaginare come mobili: come la superficie del mare, per esempio, ma di un mare senza onde. Immergiamo la mano e diamo una mescolata: abbiamo effettuato una trasformazione geometrica. Ovvero abbiamo preso dei punti e li abbiamo spostati da un'altra parte. Un oggetto matematico che prende i punti del piano e li muove si chiama trasformazione geometrica.

Esempi pratici: scriviamo le formule che ci interessano su un foglio, lo inseriamo in un fotocopiatore e produciamo un meraviglioso francobollo che contiene tutto quello che ci serve. Abbiamo stabilito una trasformazione geometrica tra i punti del foglio e quelli della fotocopia (non importa molto se i due fogli sono diversi, possiamo immaginarli come sovrapposti e trattarli come uno solo).

Oppure: un telefilm in formato 4:3 viene proiettato su un televisore in formato 16:9 senza bande nere ai lati: il quadro è deformato, e abbiamo fatto una trasformazione che prende i punti del piano (dello schermo televisivo) e li dilata.

E infine: prendiamo un foglio e, semplicemente, lo capovolgiamo. Ciò che era in alto ora è in basso, e viceversa: abbiamo nuovamente spostato i punti del piano; ma non tutti, se ci pensiamo bene: il centro del foglio, ad esempio, è rimasto fermo.

E così abbiamo chiarito il primo termine: trasformazione.

Erlangen 1872 — Che cosa è la geometria?

Che cosa è la geometria? Se lo chiediamo a un bimbo delle elementari, probabilmente ci risponderà che non lo sa spiegare bene, perché a volte si confonde un po' con la geografia. Un ragazzino delle medie ci risponderà che è quella materia scolastica in cui si studiano le figure e le misure. Se arriviamo alle superiori, un ragazzo del biennio si metterà le mani nei capelli pensando alla geometria euclidea, ai suoi teoremi e alle sue dimostrazioni senza numeri. Un ragazzo del triennio farà altrettanto, pensando invece alla geometria analitica e alle sue formule. Infine, uno studente universitario risponderà che la geometria è la materia più difficile del primo anno, perché è piena di formule, matrici, determinanti, autovettori, trasformazioni lineari, ma di figure non se ne vede una.

Se andiamo a dare un'occhiata alla voce Geometria di Wikipedia, troviamo elencate almeno dieci geometrie diverse, tanto per dire.

Poi nel 1872 è arrivato Felix Klein, che ha proposto di vedere tutte queste geometrie da un unico, nuovo, punto di vista. Nel suo programma di Erlangen Klein ha spiegato che una geometria consiste nello studio delle proprietà di uno spazio che sono invarianti rispetto ad un gruppo di trasformazioni.

Eh?, diranno tutti gli studenti di ogni ordine e grado.

Si tratta di capire i termini della questione, spiegare cosa significano invariante, gruppo, trasformazione. Poi è facile.

Carnevale della Matematica #28

One would be hard put to find a set of whole numbers with a more fascinating history and more elegant properties surrounded by greater depths of mistery — and more totally useless — than the perfect numbers.

Martin Gardner

La bellezza dei numeri perfetti è stata ammirata, anche con una sorta di timore mistico, dai matematici di tutti i tempi.

I pitagorici, ad esempio, associavano il numero 6 al matrimonio, alla salute e alla bellezza.

Filone di Alessandria, nel primo secolo, associò 6 alla perfezione e al movimento dei corpi organici, i quali possono spostarsi lungo sei direzioni (alto, basso, avanti, indietro, destra, sinistra). Oggi parleremmo di gradi di libertà di un corpo rigido.

Nicomaco, nella sua Introduzione all'aritmetica, scritta intorno all'anno 100, osserva l'armonia dei numeri perfetti, in equilibrio tra i numeri difettivi e i numeri abbondanti, e fa notare come 6, 28, 496 e 8128 siano i soli numeri perfetti compresi negli intervalli di estremi 1, 10, 100, 1000 e 10000. Inoltre, essi terminano alternativamente con la cifra 6 oppure con la cifra 8.

Sant'Agostino, vissuto a cavallo tra il quarto e quinto secolo, considerava il 6 come un numero veramente perfetto: Dio creò il mondo in 6 giorni proprio per dimostrare la perfezione della sua opera. Allo stesso modo Alcuino di York, vissuto nel settimo secolo, notava come la cosiddetta seconda origine fosse invece imperfetta, dato che si è basata sul numero 8, un numero difettivo (otto erano infatti gli uomini contenuti nell'arca di Noè: Noè stesso, i suoi tre figli e le loro quattro mogli).

Roswitha di Gandersheim, badessa del convento di Gandersheim, in Sassonia, considerata la prima poetessa tedesca (anche se scriveva solo in latino), in uno dei suoi drammi, intitolato Sapientia e scritto nel decimo secolo, elenca i primi quattro numeri perfetti.

I numeri perfetti erano così importanti per gli ebrei che il rabbino Josef ben Jehuda Ankin suggerì, nel suo libro dedicato alla cura dell'anima e scritto verso la fine del dodicesimo secolo, di studiare le loro proprietà.

Ericio Puteano, un enciclopedista, nei suoi scritti del 1640 riferisce l'associazione tra Venere e il numero 6, in quanto formato dalla diade (femminile e pari) e la triade (maschile e dispari).

Nei secoli seguenti i matematici hanno continuato a studiare le proprietà dei numeri perfetti, raccogliendo un notevole numero di risultati (e anche di congetture errate).

Se indichiamo con σ(n) la somma dei divisori di n (compresi 1 e n stesso), allora un numero N si dice perfetto se σ(N) = 2N. Se invece σ(N)<2N, allora il numero si dice difettivo, mentre se σ(N)>2N, allora il numero si dice abbondante.

Se un numero N è perfetto, allora la somma dei reciproci dei suoi divisori è sempre uguale a 2.

Euclide, nella proposizione 36 del libro IX degli Elementi, afferma (in forma un po' più discorsiva) che se 2ⁿ-1 è primo, allora N = 2^n-1(2ⁿ-1) è perfetto. Quindi la ricerca dei numeri perfetti è legata alla ricerca di numeri primi nella forma 2ⁿ-1, detti numeri di Mersenne.

Ogni numero primo di Mersenne genera un numero perfetto, e viceversa ogni numero perfetto genera un primo di Mersenne. Questo risultato è noto come teorema di Euclide-Eulero.

Il criterio di Cataldi-Fermat può essere d'aiuto: se 2ⁿ-1 è primo, allora n è primo.

Eulero, in un teorema pubblicato dopo la sua morte, ha dimostrato che se N è un numero perfetto pari, allora esso può essere scritto nella forma N = 2^n-1(2ⁿ-1), dove 2ⁿ-1 è primo.

Se N è un numero perfetto pari, allora è anche un numero triangolare.

Se N è un numero perfetto pari (e quindi può essere scritto come 2^n-1(2ⁿ-1)), allora n = 1³ + 2³ + … + (2^(n-1)/2-1)³.

Sempre utilizzando la notazione del teorema precedente, se N è un numero perfetto pari allora, scritto in base 2, possiede 2n-1 cifre; le prime n sono uguali a 1, le ultime n-1 sono zero.

Ogni numero perfetto pari termina con la cifra 6 o con la cifra 8.

Se si sommano le cifre di un numero perfetto pari (escluso 6) e si ripete il processo fino ad avere una sola cifra, si ottiene 1.

Per quanto riguarda i numeri perfetti dispari, non sappiamo quasi niente. Non sappiamo nemmeno se esistono; forse non esistono. Se esistono, sono sicuramente maggiori di 10³⁰⁰, forse anche di 10⁵⁰⁰.

Concludiamo la storia con un'affermazione di Sylvester, del 1888: a prolonged meditation on the subject has satisfied me that the existence of any one such [odd perfect number] — its escape, so to say, from the complex web of conditions which hem it in on all sides — would be little short of a miracle.

Tutto questo, comunque, è per introdurre il Carnevale della Matematica numero 28. Il prossimo Carnevale-perfetto sarà il numero 496, che si terrà il 14 dicembre 2051, non si sa ancora dove.

Il prossimo Carnevale, invece, sarà il numero 29 e verrà ospitato dai Rudi Matematici.

E ora andiamo a incominciare.


.mau., per quanto riguarda la categoria Povera matematica, ha scovato due errori: in Fanno sbagliare i conti già ai piccoli si vede come sia difficile fare una sottrazione, mentre in Chilometro e mezzo quadrato fa notare come non sia proprio corretto confondere misure lineari con misure di superficie.

Per la categoria link, il nostro ci segnala il CD con la raccolta completa dei libri di Martin Gardner dallo Scientific American a prezzo scontato, mathURL e asciiTeX, due sistemi per inserire formule matematiche nei propri siti e math@stackexchange, una nuova community matematica in via di sviluppo (e in inglese, naturalmente).

Per la categoria recensioni, ecco due libri: Il matematico curioso, che cerca di mostrare come la matematica spunti dappertutto, se la si sa vedere; Mathematical Recreations, storia della matematica ricreativa a.G. (cioè avanti Gardner).

Per la categoria giochi, il Futoshiki: un sudoku dove i numeri sono davvero numeri e non segnaposto.

Per la categoria io, un importante annuncio: Ho anch'io un numero di Erdős!

Infine, per la mega-categoria Il Post (ovvero un altro blog matematico), abbiamo: Il paradosso di san Pietroburgo: da un banale gioco di testa o croce non solo si può arrivare a una vincita potenzialmente infinita, ma addirittura si ha che la vincita media è infinita! Proseguiamo poi con Dal paradosso dell'Alabama ai deputati frazionari: il metodo proporzionale sembra essere il più equo per suddividere i deputati da eleggere; ma anche in questo caso sorgono dei paradossi. Poi abbiamo Parole matematiche: parabola: che cosa hanno in comune i racconti evangelici con l'antenna satellitare? E ancora  Il teorema di Pitagora: il teorema più famoso della geometria merita indubbiamente una trattazione a sé. Seguono Paul Erdős: i matematici sono spesso dipinti come persone piuttosto strane, anche se in genere non pericolose — beh, Erdős ha pienamente diritto di essere inserito in questa categoria; La funzione base-13 di Conway: un post da leggere in parallelo a Continuità (pubblicato qui): noi siamo abituati a pensare alle funzioni come qualcosa di disegnabile, ma non è che sia sempre così, anzi — ecco un esempio non molto noto di funzione assolutamente incredibile; Parole matematiche: prodotto, fattore: due parole al prezzo di una: stavolta l'origine è latina e non greca, e soprattutto hanno in comune qualcosa in più di quanto si potrebbe pensare a prima vista; La serie armonica: molte successioni hanno una somma infinita, altre hanno una somma finita — la serie armonica va sì all'infinito, ma così piano che uno magari non se ne accorge nemmeno. Infine, Problemini matematici ferragostani: per una volta, anche il blog di matematica si prende qualche libertà.

Ho scritto infine, ma in realtà non è così: il 9 agosto ha iniziato a girare la notizia che forse è stato dimostrato uno dei problemi del millennio, la congettura più importante nel campo dell'informatica; pare cioè che sia vero che P != NP: .mau. ne ha parlato in P != NP (o no?), fornendo anche una spiegazione del problema che vede coinvolti Gastone, Paperino e Qui, Quo, Qua.


Dioniso, continuando la trattazione già pubblicata nello scorso carnevale, ci propone l'appendice numero 1 e la numero 2 alla sua serie Chi vincerà il mondiale del 2014? Una questione di Logica intuizionista? Infine, un approfondimento alla appendice 2: Tentativo di dimostrazione che nella logica intuizionista (I → ¬¬I), ma non (¬¬I → I). Qui si può leggere o scaricare l'opera completa.


Gianluigi Filipelli ha mandato una lista dei suoi post corredati tutti con un'ottima e abbondante descrizione: lascio quindi la parola a lui per il commento ai suoi pezzi. Dal suo blog personale, dropsea, abbiamo:

Calcolare le equazioni con Geogebra: due applet di Geogebra realizzate da due gruppi di miei ex-studenti del primo superiore: Stefano, Davide, Fabio, Alessandro. Un modo per risolvere le equazioni come intersezione tra figure geometriche.
Un problema pitagorico: un altro post realizzato grazie al contributo delle applet di miei ex-studenti dell'ultimo anno scolastico. In questo caso Federica, Hazel, Giuditta, Stefano, Matteo hanno risolto un problema pitagorico che ho trovato sul blog di Annarita utilizzando Geogebra.
Integrali e polilogaritmi: una collega mi ha proposto un integrale. Ho provato a risolverlo, ma vedendo che arrivavo a un certo punto e mi bloccavo, ho... barato usando Wolfram Alpha... Ed ecco la sorpresa!

Da Science Backstage, invece, Gianluigi propone i seguenti post:

L'algoritmo del destino: il mitico John Conway, oltre al famoso gioco della vita, ha realizzato anche molte altre cose nell'ambito della ricerca matematica ricreativa. In particolare un algoritmo con il quale è in grado di calcolare a mente il giorno della settimana corrispondente a una certa data. &Ergave; stato, però, recentemente proposto un aggiornamento da parte di Chamberlain Fog, e quindi anche di questo si va a discutere nell'articolo.
Scalando il Tourmalet: di tutti i post dedicati al Tour de France, questo è quello che contiene esplicitamente la matematica, grazie alla pendenza di una retta.
La storia di Achille e della tartaruga: un nuovo Rompicapo, tra fisica e matematica. Se nella prima parte si affronta il famoso paradosso di Zenone dal punto di vista della fisica, nella seconda si esamina un nuovo paradosso che coinvolge Achille e la tartaruga, questa volta elaborato dal grande Carroll.
Terne non pitagoriche, aree intere: sappiamo tutti che le terne pitagoriche altro non sono che tre numeri interi che verificano il Teorema di Pitagora. È allora possibile trovare, data l'ipotenusa, due altri cateti non necessariamente naturali che danno come area del triangolo un numero intero? Provo a rispondere con questo piccolo problemuccio geometrico. Alla fine anche una applet Geogebra (giusto per non farsi mancare niente!)


Peppe Liberti ha parlato di Bessel e delle sue funzioni in Funzioni sulla sabbia, e poi si è lamentato di un certo uso della matematica in Cosa non sopporto della matematica (basta la frase “i misteri della scienza” per spiegare contro cosa se la prende Peppe?)


Maurizio ha poi scritto Ma quasi tutti sanno che…, dove si può trovare un'applicazione del principio di induzione per dimostrare una proprietà della somma dei cubi di tre numeri maturali consecutivi, e Joseph Ludwig Raabe, un breve profilo del matematico svizzero con un'applicazione del suo criterio di convergenza per le serie numeriche.


Claudio Pasqua, da Gravità Zero, partecipa con il post intitolato “Sua Altezza” Talete di Mileto, in cui riporta e amplia un articolo comparso su MondoErre riguardante il matematico e filosofo greco. Il post si conclude con un semplice problemino, intitolato L'elefante e il topolino (semplice ma non stupido, non fatevi ingannare…).


Annarita Ruberto ci manda, come al solito, una lunghissima serie di contributi. Per quanto riguarda la storia della matematica e la divulgazione, abbiamo:

Talete: Il Fondatore Della Matematica Greca [Scheda Storica]: una scheda storica sul grande Talete.

Perché Non Usiamo Più I Numeri Romani?: l’articolo riporta un brano estratto da libro di Clifford Pickover Le Meraviglie dei Numeri, in cui un ragazzo pone la domanda “Perché non usiamo più i numeri romani?” al dottor Googol. Un “Googol” è un numero pari a 10mila decaexilioni, ovvero un numero intero esprimibile con 1 seguito da 100 zeri. Ma il Dottor Francis O. Googol «è un personaggio di cui Clifford Pickover narra le avventure matematiche». Sarà, infatti, il Dottor Francis O. Googol a «trasportarci verso nuovi mari, rendendo più profonde le acque e allargando gli orizzonti». Nel brano sono contenuti due rompicapo con i numeri romani.

Perché Si Usa IIII E Non IV Sui Quadranti Di Alcuni Orologi?: l'articolo nasce da una domanda posta da un lettore in un commento al post "Perché non usiamo più i numeri romani?".

I Numeri Di Mozart: che la musica di Mozart avesse a che fare con i numeri e con la matematica è cosa risaputa. Grazie a un progetto promosso da alcuni insegnanti inglesi si è scoperto, infatti, che ascoltare la musica mozartiana migliora le performance degli studenti in ambito matematico. L'articolo riporta un brano tratto dalla Magia dei Numeri di Clifford Pickover.

L'Eredità Arabo-Indiana [Scheda Storica]: il contributo dei matematici indiani e di quelli arabi allo sviluppo del pensiero matematico universale.

Il Problema Di Euler: problema contenuto nella Introduzione all’algebra di Euler, che impressionò Stendhal.

Leonardo Pisano (detto Fibonacci).

Per quanto riguarda la didattica, annarita ha scritto:

La Tavola Pitagorica E I Numeri Quadrati: un contributo di Bruno Berselli per Matem@ticaMente. Sappiamo che solitamente la Tavola pitagorica viene presentata come uno schema quadrato di 10×10 o 12×12. Può allora essere interessante chiedersi se essa abbia qualche caratteristica non ovvia legata ai numeri quadrati. Ne esiste una, in effetti, pur non essendo l’unica, che viene analizzata nell'articolo.

Problema Con Quadrato, Rettangolo E Triangolo Rettangolo, Risolto Con GeoGebra.


Paolo Pascucci ha preparato una serie di interventi dal titolo Aritmetica e Cervello: l'aritmetica è connaturata ai cervelli di molti animali, oppure no? Ecco qua il primo post, il secondo e il terzo.


Popinga partecipa con un solo, denso, contributo: La matematica visionaria di Yi Sang. L’opera poetica del coreano Yi Sang, di cui ricorre quest’anno il centenario della nascita, è caratterizzata da versi liberi, originali grafie, giochi di parole, che disorientano il lettore, allora come oggi. Spesso il carattere e l’impaginazione hanno un aspetto matematico, evocando formule numeriche e combinatorie, con simboli, parentesi, punti, deliberata sovversione degli spazi. Inoltre i testi della traslitterazione coreana rivelano un gioco occulto di regole, di ripetizioni, di simmetrie e di giochi di specchi impossibili da rendere nel nostro alfabeto.


Questo mese abbiamo una new entry: si tratta di Melassa, che ha scritto un post intitolato Il soggetto noto. Il matematico Oliver Byrne diede alle stampe nel 1847 The first six books of the elements of Euclid: in which coloured diagrams and symbols are used instead of letters for the greater ease of learners, definito dall’American Scientist il più bel libro di matematica di tutti i tempi. Byrne concepì questa edizione di Euclide come un sistema completamente nuovo per imparare la geometria, riducendo al minimo il testo scritto e dando forma visuale alle informazioni. Il suo testo da un punto di vista di didattica della matematica è assolutamente inutile, ma le sue composizioni geometriche anticipano l’arte di Mondrian e di tanti altri pittori del Novecento.


I Rudi Mathematici ci scrivono direttamente dalla loro riunione di comitato di redazione, proponendoci i seguenti contributi: uno dei migliori compleanni mai usciti dalla penna di Alice, quello del misconosciuto Robert Hooke, a cui fa buon seguito uno dei migliori Zugzwang! (si sente che stanno facendo la riunione in terra tedescofona?), i Secondi scivolosi secondo il GC. Segue poi la soluzione al quiz pubblicato su Le Scienze (i Rudi si chiedevano se io volessi pubblicarlo sul carnevale della matematica, e hanno quindi aggiunto la seguente descrizione: considera che l'occasione di vedere Alice in costume da bagno è davvero rara. Vedete voi se dare un'occhiata o no). Segue poi un bel post, che ha fortemente voluto Rudy: si tratta di indicare i libri di argomento (più o meno) matematico per l'estate, per le vacanze, per la vita e per tutto il resto. A dire il vero hanno rubato l'idea ad un blog confratello (quello di Daniela Ovadia), ma tanto l'idea l'aveva già rubata anche lei… Si continua poi con altri due compleanni: quello di P.A.M. Dirac, sempre dalla penna di Alice, e quello del glorioso Erwin Schroedinger. Ma a tenere un blog son buoni tutti: i nostri sono anche arrivati a pubblicare il numero 139 di una prestigiosa rivista di matematica ricreativa; dite voi se è poco.

Il Carnevale finisce qui: divertitevi.

Aggiornamento

Grazie a .mau. che ha tirato fuori l'argomento, e grazie a questo sito di ricerche di collaborazioni, posso gioiosamente annunciare che il mio numero di Erdős è (minore o uguale a) 5.

Continuità

Un giorno un monaco si recò a meditare in cima a una montagna. Partì all'alba dal monastero, e cominciò la salita. Durante la salità si fermò alcune volte per riposare, per mangiare e per godersi il panorama, e finalmente, verso sera, arrivò sulla vetta, dove rimase per qualche giorno.

Il monaco meditava sugli argomenti più diversi: alcuni molto privati, altri invece di interesse pubblico. Un giorno dedicò molto tempo a ragionare sul fatto che, in ogni momento, lungo l'equatore esistono due punti, uno agli antipodi dell'altro, in cui la temperatura dell'aria è la stessa.

E questo fatto non dipende da una particolare proprietà della temperatura dell'aria. Esistono infatti anche altri due punti, sempre antipodali, in cui la pressione dell'aria è la stessa, e altri due punti in cui la concentrazione di anidride carbonica è uguale. E si potrebbe andare avanti con tanti altri esempi.

Non è nemmeno necessario trovarsi sull'equatore: va bene un qualunque cerchio massimo sulla terra. A cosa è dovuta, si chiese il monaco, questa strana proprietà?

E si mise a disegnare sul terreno.

“Vediamo”, pensò il monaco, “se scelgo due punti a caso A e B, uno agli antipodi dell'altro, non è detto che la temperatura in quei due luoghi sia la stessa. Se indico con T(x) la temperatura in un punto qualsiasi, ho che la differenza di temperatura nei due punti che ho scelto è uguale a T(A)-T(B), che indico con d”.

Poi il monaco si mise a passeggiare un po' intorno alla figura che aveva disegnato. E gli venne un'idea:

“Ehi, ma se io ruoto il segmento AB di 180 gradi, e ricalcolo la differenza di temperatura, ora naturalmente mi risulterà l'inverso di prima, cioè -d”.

“Ma quindi”, continuò tra sé e sé, “se la differenza di temperatura prima vale d, e poi vale -d, in un qualche punto deve valere zero!”. E fece un altro disegno.

“Naturalmente questo vale solo se la curva è una vera curva, cioè se non fa strani salti. Se ben ricordo, i matematici chiamano queste curve continue. Chiamerò questo teorema proprietà dei valori intermedi: se una funzione è continua, allora essa assume tutti i valori compresi tra il suo minimo e il suo massimo”.

Dopo tutti questi ragionamenti, il monaco pensò che fosse ora di mangiare. Si trovava lì vicino un tavolino rotondo, di legno, con quattro gambe, costruito in passato da qualche altro monaco che era stato in quei luoghi a meditare. Il monaco lo sistemò sul terreno, vicino ai due disegni che aveva fatto prima, e si accorse che non era stabile.

“Ci risiamo,” pensò, “ogni volta che si sistema un tavolino in un luogo non perfettamente piano, c'è il problema della stabilità. L'aveva detto Euclide che con tre gambe un tavolino non balla, ma questo ne ha quattro”.

E così, invece di mangiare, il monaco si mise a studiare il problema. Si chinò ad esaminare le gambe del tavolo:

“Vediamo un po'. Ecco qua, ci sono tre gambe appoggiate per bene sul terreno, e la quarta invece è per aria. E dire che i miei confratelli sono molto precisi, le gambe hanno tutte la stessa lunghezza. Già, è proprio colpa del terreno, che ha qualche gobba”.

“Ragioniamo”, si disse. “Indico con A la gamba che non tocca terra, e con B, C e D le altre tre. Ora, se lascio C e D fisse dove sono, e spingo un po' verso il basso A e B, riesco a fare toccare A sul terreno. In questo modo però B è affondata un po'”.

“Ma se ruoto il tavolo di 90 gradi, in modo che A vada al posto di B, B al posto di C, e naturalmente C al posto di D e D al posto di A, ora sarà la gamba che ho indicato con A ad essere affondata nel terreno”.

“Ah-ha!”, esclamò, “ma dato che all'inizio della rotazione A si trovava in aria, e alla fine si trova sotto terra, esisterà un punto in cui A tocca esattamente terra, e quindi il problema è risolto, il tavolino è stabile, e posso finalmente mangiare”.

Il monaco trascorse molti giorni sulla cima della montagna a meditare. Mentre si trovava lassù, un gruppo di matematici cercò, in maniera naturalmente indipendente, di formalizzare la dimostrazione della stabilità del tavolino con quattro gambe. Non fu una cosa semplice.

Nei giorni successivi, il monaco meditò sulla proprietà dei valori intermedi. “Che sia una proprietà caratteristica delle funzioni continue?”, si chiese. “È vero che se, dati due punti qualsiasi a e b, una funzione assume tutti i valori compresi tra f(a) e f(b), allora è continua?”.

Ma ormai era tempo di tornare a valle, e il monaco dovette abbandonare questi pensieri, o quantomeno rimandarli ad un altro momento. Egli partì all'alba e, seguendo la stessa strada compiuta durante la salita, arrivò verso sera al monastero. 

“Ehi, ora che ci penso, c'è stato un punto del percorso in cui durante i due viaggi io sono passato alla stessa ora”.

Le tre leggi della robotica

Il file robots.txt di last.fm è fatto così:

User-Agent: *
Disallow: /music?
Disallow: /widgets/radio?
Disallow: /show_ads.php

Disallow: /affiliate/
Disallow: /affiliate_redirect.php
Disallow: /affiliate_sendto.php
Disallow: /affiliatelink.php
Disallow: /campaignlink.php
Disallow: /delivery.php

Disallow: /music/+noredirect/

Disallow: /harming/humans
Disallow: /ignoring/human/orders
Disallow: /harm/to/self

Allow: /

Call for papers

Oh, non è che adesso andate tutti in vacanza e vi dimenticate che qua tra poco ci sarà il Carnevale della Matematica numero 28, vero?