«Qual è la frazione generatrice di un numero decimale periodico?».
«Eeh?».
«A cosa è uguale zero virgola tre periodico?».
«A un terzo».
«Perché?».
«Perché sì, è vero!».
«Ottimo esempio di dimostrazione…».
«È vero o no che 1/3 è uguale a 0.(3)?».
«Certo, ma volevo sapere se sai cosa c'è sotto».
«Veramente no».
«C'è una formuletta interessante, che riguarda la serie geometrica».
«Uhm».
«La serie geometrica è questa cosina qui:».
«Una somma infinita. Ha senso?».
«A volte sì».
«Come, a volte? Come è possibile?».
«Cominciamo dal caso finito: se n è un numero naturale, quella somma diventa uguale a:».
1 + q + q2 + q3 + … + qn.
«Ok».
«Ora troviamo una espressione più semplice».
«Non va bene quella?».
«Non tanto: ci danno molto fastidio i puntini».
«E perché?».
«Perché se vogliamo capire cosa succede quando n diventa sempre più grande, quella somma diventa una espressione infinitamente lunga, e non sappiamo come gestirla».
«Quindi tu vorresti eliminare i puntini? Si può?».
«Sì. Alle superiori dovrebbero averti insegnato come si fanno le divisioni tra polinomi. Io confido nel fatto che tu le sappia ancora fare…».
«Ehm».
«Grazie alla regola della divisione tra polinomi, puoi verificare tu stesso questa uguaglianza:».
«Mh».
«Altrimenti ti fidi».
«Mi fido sulla parola senza problemi».
«Vabbé. Allora, vedi che la seconda espressione è più semplice della prima, anche se contiene una divisione».
«Sì, se ti danno tanto fastidio i puntini, la seconda espressione non ne ha».
«Prova allora a pensare a cosa succede man mano che n diventa sempre più grande».
«Quel numeratore diventerà sempre più grande, dato che è elevato alla n+1».
«Siamo sicuri?».
«Certo, se elevo un numero a potenza questo aumenta».
«Prova a elevare un mezzo».
«Un quarto. Oops. Ehm».
«Fai una osservazione intelligente».
«Se elevo alla n un numero maggiore di 1, allora ottengo un risultato maggiore del numero di partenza. Altrimenti il risultato è minore».
«Prova a prendere -2, che è sicuramente minore di 1».
«Risulta 4. Uffa. Allora: se elevo alla n un numero maggiore di 1 oppure minore di -1, ottengo un risultato maggiore, altrimenti è minore».
«Calcola -2 elevato alla 3».
«Fa -8, argh, è minore. Ma quanti casi ci sono?».
«Se vuoi semplificare un po' il numero di casi, devi usare il valore assoluto. Se elevi alla n un numero in valore assoluto maggiore di 1, ottieni un numero che, in valore assoluto, è maggiore. Se elevi invece alla n un numero in valore assoluto minore di 1, allora ottieni un numero che, sempre in valore assoluto, è minore di quello di partenza».
«Ho capito. Mi pare che tu abbia lasciato fuori 1 e -1».
«Sì, è vero. Se q = 1, la formula che ti ho scritto prima non vale».
«Perché?».
«Perché al denominatore risulterebbe zero».
«Ah, già. E allora?».
«Allora non la usiamo, ma non è difficile capire come stanno le cose. Se q = 1, la somma delle potenze di q diventa semplicemente una somma di tanti 1».
«Che aumenta sempre».
«Infatti. Se invece q = -1 la formula è valida, e il numeratore di quella frazione diventa alternativamente uguale a 0 oppure a -2».
«Una schifezza».
«Sì. Noi siamo interessati al caso di q minore di 1 in valore assoluto».
«Perché proprio quello?».
«Perché in quel caso, quando n diventa infinitamente grande, la potenza qn+1 diventa infinitamente piccola».
«E allora possiamo trascurarla, quando facciamo i calcoli?».
«Esatto. I Veri Matematici parlano di limite, c'è tutta una teoria sotto che motiva in modo preciso i vari passaggi, ma a noi interessa avere intuito il risultato».
«Che sarebbe questo?».
«Esatto. Quando q è, in valore assoluto, minore di 1, si dice che la serie geometrica converge, e il risultato viene chiamato somma della serie. Mentre q viene detto ragione della serie».
«Bello».
«E ora puoi calcolare quanto vale 0.(3)».
«Con la serie?».
«Sì».
«E come faccio?».
«Cosa significa zero virgola tre periodico?».
«Che ci sono infiniti 3 dopo la virgola».
«Che significato ha il primo di quei 3?».
«Uhm, boh, 3 decimi?».
«Esatto. E il secondo?».
«3 centesimi».
«E così via. Puoi quindi scrivere 0.(3) come una somma di tante frazioni:».
3/10 + 3/100 + 3/1000 + …
«Una serie geometrica?».
«Esatto».
«Ma non capisco quanto vale q».
«Te la scrivo in un altro modo:».
3/10 (1 + 1/10 + 1/100 + …).
«Ah, ho capito! La somma tra parentesi è la serie geometrica!».
«Di ragione?».
«Di ragione 1/10».
«Che è minore di 1, in valore assoluto. Quindi?».
«Quindi converge».
«A quale valore?».
«A 1/(1-1/10)».
«Cioè 1/(9/10), che è uguale a 10/9».
«E se adesso la moltiplico per il coefficiente 3/10, ottengo proprio 3/9, cioè 1/3. È la regolina che mi avevano insegnato alle medie per trovare la frazione generatrice di un numero decimale periodico, ora mi ricordo».
«Ottimo».
«Finalmente qualcosa di utile!».
«ALLORA?».
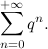
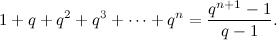
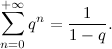
3 commenti:
Bello! :)
c'è un errore di battitura verso la fine:
3/10 + 3/100 + 3/100 + …
dovrebbe essere:
3/10 + 3/100 + 3/1000 + …
Giusto. Grazie, correggo.
Molto interessante che si puo' generalizzare al generico numero periodico:
SE: x = 0.(P1P2...Ph)
essendo Pj= j-esima cifra costituente il periodo
ad essa si puo' attribuire una serie geometrica di ragione 1 / 10^h che compare
nella espressione di x
E ALLORA:
10^h P1 P2 Ph
x = ---------- ( ---- + ----- + ... + ------ )
10^h - 1 10 100 10^h
Posta un commento