Solidi platonici

Vediamo di utilizzare la formula di Eulero, che non si dica che le cose che fanno i matematici non servono mai a niente.

“Uh, è la prima volta che sento un matematico preoccuparsi dell'utilità della matematica”.

“No, in realtà volevo darmi un po' di tono. In effetti i Veri Matematici non si preoccupano affatto delle applicazioni che possono avere le loro scoperte”.

“Ah, ecco, mi sembrava. E per cosa, allora, vorresti usare la formula di Eulero?”.

“Per analizzare i poliedri convessi regolari, cioè i poliedri convessi che hanno le facce tutte congruenti tra loro. Inoltre, le facce devono essere poligoni regolari”.

“Ah, ok, quindi diciamo che sono i solidi più regolari che ci siano”.

“Già. Ti avverto che dobbiamo usare un po' di formule, ma sono formule semplici”.

“Va bene, sono pronto”.

“Per prima cosa, indichiamo con n il numero di spigoli per ciascuna faccia. Quindi, se le facce saranno tutte dei triangoli equilateri, avremo n = 3; se saranno quadrati, avremo n = 4, e così via”.

“Quanto si può andare avanti?”.

“Poco. Lo vediamo tra un momento”.

“Bene. Poi?”.

“Poi indichiamo con m il numero di spigoli incidenti in ciascun vertice. Data la regolarità della figura, m deve essere costante per ogni vertice”.

“Giusto”.

“Ora cominciamo con qualche calcolo. Con nF abbiamo indicato il numero di spigoli per ciascuna faccia, moltiplicato per il totale delle facce. Siccome due facce si incontrano sempre in uno spigolo, questa moltiplicazione ci darà il doppio del totale degli spigoli, cioè 2S”.

“Ok, ogni spigolo viene contato 2 volte perché compare sempre in due facce che si toccano”.

“Perfetto. Ora, con mV indichiamo la moltiplicazione del numero di spigoli incidenti in ciascun vertice per il totale dei vertici. Anche qui ogni spigolo viene contato due volte, perché ogni spigolo ha due estremi: dunque anche con questa moltiplicazione otteniamo il doppio del totale degli spigoli, cioè 2S”.

“Va bene. Direi che possiamo riassumere il tutto con la seguente uguaglianza:”.

nF = 2S = mV.

“Giusto. Quindi V è uguale a nF/m e S invece è uguale a nF/2”.

“Fin qua ci sono”.

“Ora ci ricordiamo di fatti vedere sabato alle 2”.

“Ok, quindi F + V - S = 2. Cosa devo fare?”.

“Devi sostituire al posto di V e S le due espressioni che hai trovato prima”.

“Bene: viene F + nF/m - nF/2 = 2”.

“Ora togliamo i denominatori, moltiplicando a destra e a sinistra per 2m”.

“Per ora è facile, viene 2mF + 2nF - mnF = 4m”.

“Ora, per semplicità, raccogliamo a fattore comune F”.

“Ecco: F(2m + 2n - mn) = 4m”.

“Benissimo. Naturalmente 4m è un numero positivo, giusto?”.

“Certamente: m è il numero di spigoli incidenti in ciascun vertice”.

“Molto bene. Anche F è positivo, perché rappresenta il numero di facce”.

“Certo. Ah, ho capito dove vuoi arrivare: l'espressione tra parentesi, cioè (2m + 2n - mn), è positiva pure lei”.

“Bravo. Aggiungiamo il fatto che n deve essere maggiore o uguale di 3, sei d'accordo anche su questo?”.

“Certo, una faccia deve essere almeno un triangolo, quindi almeno tre lati deve averli”.

“Allora cominciamo con un po' di passaggi”.

2m + 2n - mn > 0,
2m > mn -2n = n(m - 2)

“Fin qua ci sono: hai portato dall'altra parte l'espressione mn - 2n e hai raccolto a fattore comune n”.

“Bene. Ora, ricordandoci che n deve essere maggiore o uguale di 3, possiamo andare avanti così”.

2m > n(m - 2) ≥ 3(m - 2) = 3m - 6,

cioè

2m > 3m - 6

e quindi

m < 6.

“Ah, ci sono. Abbiamo trovato una limitazione per m, bello”.

“Sì, e poi ce n'è un'altra: m deve essere come minimo uguale 3, perché in ogni vertice devono congiungersi almeno 3 spigoli, altrimenti non ottieni un solido. In pratica abbiamo 4 casi da provare:  m = 3, 4, 5, 6”.

“Va bene. Cominciamo da m = 3?”.

“Sì. Teniamo sempre in mente l'uguaglianza F(2m + 2n - mn) = 4m”.

“Ok. Se provo a sostituire m = 3, risulta F(6 + 2n - 3n) = 12”.

“Semplificando, F(6 - n) = 12. Ora proviamo a sostituire i possibili valori di n e vediamo che succede”.

“Se provo con n = 3, ottengo 3F = 12, quindi F = 4”.

“Giusto, hai trovato un caso accettabile. Quanto risulta V?”.

“Avevamo detto che V = nF/m, quindi viene V = 4”.

“E quanto risulta S?”.

“Dalla formula S = nF/2 ottengo S = 6”.

“Giusto. Quindi il primo solido che abbiamo trovato ha 4 facce triangolari, 4 vertici, 6 spigoli che si incontrano a 3 a 3 sui vertici. Si chiama tetraedro”.

“Wow. Ora devo provare con n = 4?”.

“Sì”.

“Vediamo: da F(6 - n) = 12 ottengo, questa volta, 2F = 12, quindi F = 6. Allora V = 8 e S = 12”.

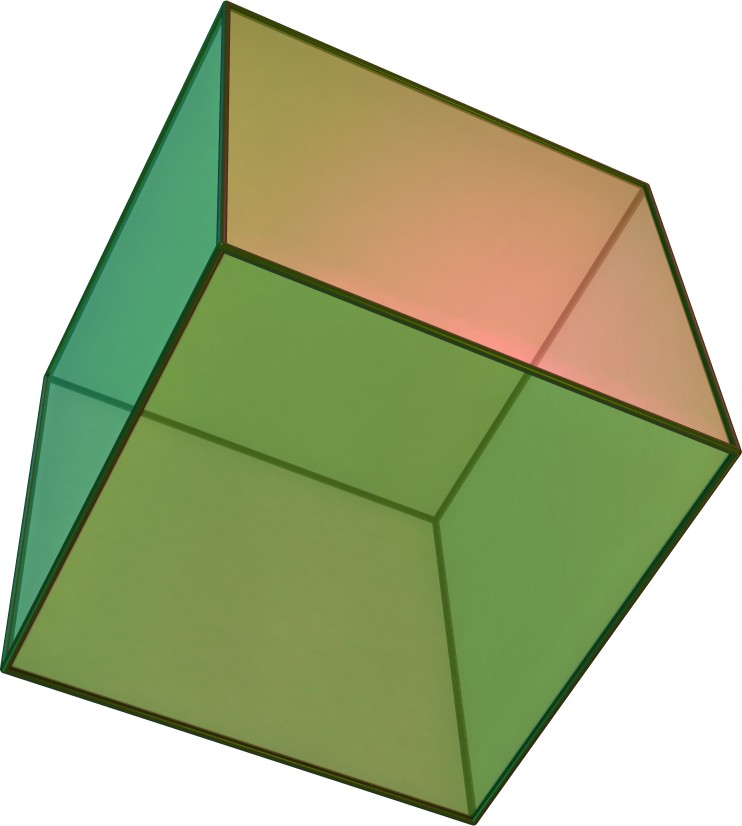
“Bene, ecco il secondo solido: ha 6 facce quadrate, 8 vertici, 12 spigoli che si incontrano a 3 a 3 sui vertici. Questo è facile: è un cubo (o anche esaedro, se vogliamo mantenere la nomenclatura in -edro)”.

“Giusto. Vado avanti, provo con n = 5, che è anche l'ultimo valore accettabile, perché con n = 6 la parentesi (6 - n) diventa 0”.

“Benissimo, vai”.

“Questa volta da F(6 - n) = 12 ricavo F = 12. Dunque V = 20 e S = 30”.

“Si tratta di un solido con 12 facce pentagonali, 20 vertici e 30 spigoli che si incontrano a 3 a 3 sui vertici. Si chiama dodecaedro”.

“Bene, ora abbiamo finito?”.

“Abbiamo finito il caso m = 3. Ora dovresti provare m = 4”.

“Ok, riparto dalla formula iniziale: F(2m + 2n -mn) = 4m. Con m = 4 viene F(8 + 2n - 4n) = 16, cioè F(8 - 2n) = 16”.

“Puoi semplificare tutto per 2”.

“Ah, giusto, allora viene F(4 - n) = 8. Uh, posso provare solo n = 3, perché già con n = 4 si azzera la parentesi, e poi aumentando n ottengo numeri negativi”.

“Bene. Vai avanti”.

“Allora, con n = 3 risulta F = 8. Quindi V = 6 e S = 12”.

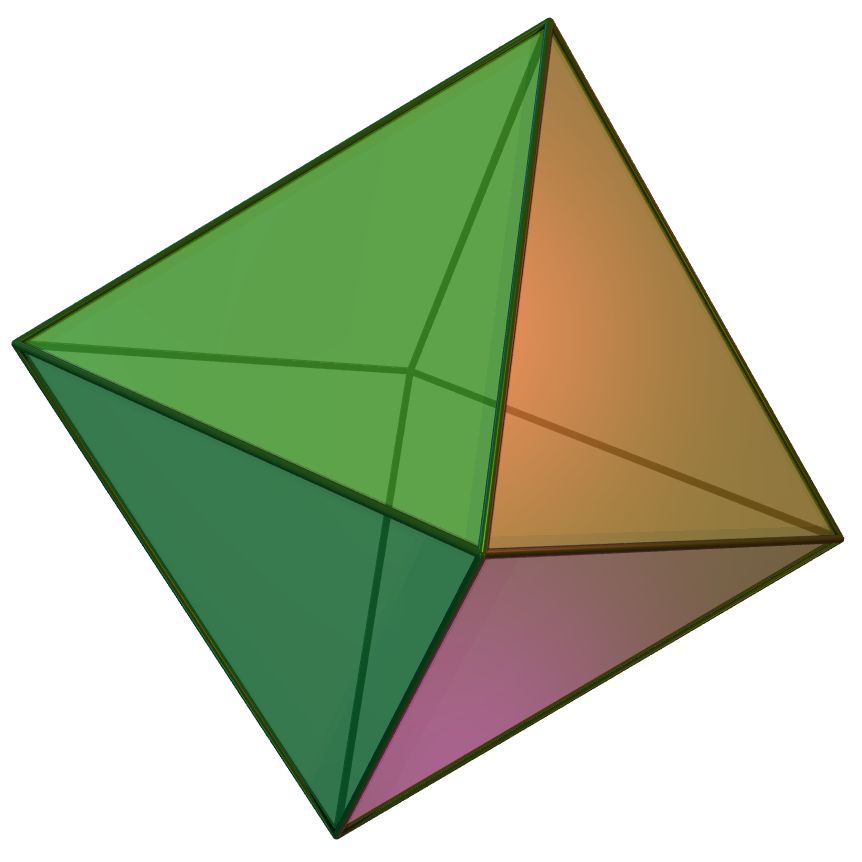
“Bene, questo è un solido con 8 facce triangolari, 6 vertici, 12 spigoli che si incontrano a 4 a 4 sui vertici. Si chiama ottaedro”.

“A questo punto devo già passare a m = 5, mi sa”.

“Sì, non hai altri casi per m = 4”.

“Allora vado. Questa volta la formula F(2m + 2n - mn) = 4m diventa F(10 + 2n - 5n) = 20, cioè F(10 - 3n) = 20”.

“Giusto”.

“Allora anche qua posso provare solo il valore di n = 3”.

“Vero. Vai pure”.

“Mi viene F = 20, quindi V = 12 e S = 30”.

“Bene, un solido con 20 facce triangolari, 12 vertici, 30 spigoli che si incontrano 5 a 5 sui vertici. Si chiama icosaedro”.

“Rimane... ehi, non rimane più niente, abbiamo provato tutti i possibili valori di m!”.

“Giusto, quindi non ci sono altri solidi, sono tutti qua, sono solo questi cinque”.

Poliedro	Vertici	Spigoli	Facce	n	m
tetraedro	4	6	4	3	3
cubo	8	12	6	4	3
ottaedro	6	12	8	3	4
dodecaedro	20	30	12	5	3
icosaedro	12	30	20	3	5

“E l'utilità pratica di questa classificazione?”.

“Eccola qua”.