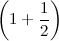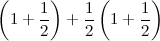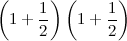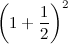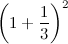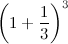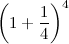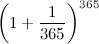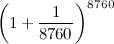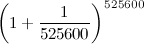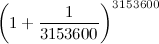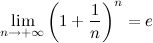Logicomix

Logicomix è un libro a fumetti che si sviluppa su tre livelli. Nel primo, i protagonisti sono gli autori, ritratti mentre stanno lavorando alla realizzazione del libro stesso. Dunque Logicomix è un libro autoreferenziale, che parla di sé. E l'autoreferenzialità è uno dei temi cardine della storia, naturalmente.

Il protagonista del secondo livello è Bertrand Russel. Il primo settembre del 1939 Hitler invade la Polonia; il quattro settembre il Regno Unito dichiara guerra alla Germania, e Russel viene invitato da un'università americana a tenere una conferenza sul rapporto tra la logica e le vicende umane. Il matematico viene accolto da un gruppo di isolazionisti, contrari all'entrata in guerra degli Stati Uniti, che invitano Russell a rinunciare alla sua lezione per unirsi, invece, alla loro protesta. Russell ribalta la situazione, e convince gli isolazionisti a partecipare alla sua conferenza con queste parole:  ma io parlerò, appunto… di ragione, e nella sua espressione più alta: la logica! Quale modo migliore per introdurre un dibattito sulla guerra?

Il terzo livello vede come protagonista la Logica: la conferenza di Russell è un lungo flashback in cui il matematico racconta la storia della sua vita, che è anche la storia della ricerca dei fondamenti della matematica, e la storia della loro crisi. In questo racconto compaiono praticamente tutti i matematici dell'epoca: Cantor, Frege, Gödel, Hilbert, Poincaré, Von Neumann, Whitehead, Wittgenstein (se vogliamo considerarlo un matematico).

Il terzo livello si conclude con le parole di Von Neumann pronunciate dopo aver assistito alla dimostrazione del teorema di incompletezza di Gödel: è la fine.

Il secondo livello si conclude invece con le parole di Russell rivolte agli isolazionsti: sentite, il mio è davvero un racconto ammonitore, una storia narrata che mette in guardia dalle soluzioni preconfezionate. Dalla semplice applicazione di formule… soprattutto per voi, che vi trovate di fronte a problemi così difficili.

Il primo livello, infine, si conclude con una rappresentazione teatrale: gli autori del libro sono invitati a teatro, ad assistere alle prove dell'Orestea. Nel finale le Furie, che voglio punire Oreste, lo inseguono fino alla città di Atene, dove egli invoca la protezione di Atena, la dea della saggezza. La quale non si comporta assolutamente come ci si aspetta da una divinità greca, perché chiama a decidere delle sorti di Oreste tutti i cittadini di Atene, dando così origine al sistema del processo giuridico democratico.


La traduzione italiana è buona; se proprio si vuole notare un difetto, questo è nella realizzazione dei fumetti: le dimensioni delle nuvolette sono identiche a quelle della versione inglese, ma la traduzione italiana è a volte un po' troppo lunga. Per fare stare l'intera frase dentro alla nuvola, a volte è stato rimpicciolito il carattere, e questo dà un po' fastidio.

Sono 352 pagine che vale la pena di leggere.

e

“Supponiamo di depositare un euro in banca a un interesse annuale del 100%…”.

“See, buonanotte”.

“È solo un esempio, lo so che non è realistico”.

“Ah, no, certo, nella classifica degli esempi poco realistici questo si trova al posto d'onore, con menzione speciale”.

“Vabbè, io vado avanti con l'esempio. A quanto ammonterà il capitale dopo un anno?”.

“Secondo le tue assurde ipotesi, alla fine dell'anno raddoppiamo il capitale, quindi due euro”.

“Esatto. Ora, non contenti del nostro interesse, andiamo alla banca e diciamo: senti, banca, ti dispiace farmi un interesse del 50% per i primi sei mesi, poi un interesse del 50% per gli altri sei mesi?”.

“E cosa cambia?”.

“Se facciamo i conti, dopo i primi sei mesi abbiamo un euro più la sua metà, che scriviamo in questo modo:”.

“E dopo gli altri sei mesi arriviamo a due euro”.

“Eh, no, ricordati che ora in banca c'è un capitale maggiore: devi fare i calcoli aumentando del 50% il capitale attuale”.

“Ah. Quindi devo calcolare il 50% di 1.5”.

“Sì. Te lo scrivo in questo modo:”.

“Sì, capisco, uno e mezzo più la metà di uno e mezzo. Perché non vuoi fare i calcoli?”.

“Perché ho uno scopo che ti apparirà chiaro tra un po'. Solite manie da matematici…”.

“Ah, ho capito, il solito sistema di complicare le cose semplici per stupire poi col gran finale”.

“Esattamente. Comunque, posso semplificare la formula un po': dato che la parentesi contenente uno e mezzo compare due volte, la prima con coefficiente uguale a uno, la seconda con coefficiente uguale a un mezzo, posso dire che alla fine ottengo una volta e mezzo quella parentesi. In formule:”.

“Che potrei anche scrivere così, a questo punto:”.

“Esatto. Anche se abbiamo scritto tutto in formule, possiamo comunque fare i calcoli: risulta che alla fine dell'anno otteniamo 2.25 euro”.

“La banca non sarà contenta”.

“Nemmeno noi, tant'è che torniamo allo sportello e domandiamo: cara banca, dato che aspettare sei mesi non mi piace molto, potresti farmi i conti degli interessi ogni quattro mesi? Quindi mi dai un terzo degli interessi dopo i primi quattro mesi, un altro terzo dopo otto mesi, e l'ultimo terzo alla fine dell'anno”.

“Vabbè, avevamo già rinunciato al realismo prima, andiamo pure avanti”.

“Se hai capito il ragionamento fatto prima, non ti è difficile seguire i calcoli adesso. Li faccio un po' più rapidamente. Dopo il primo periodo avremo in banca il seguente capitale:”.

“Sì, è come prima. Dopo il secondo dovremmo avere:”.

“Infatti. Alla fine dell'anno avremo questo risultato:”.

“Mi pare di intravedere una formula generale…”.

“Sì, esatto. Questo dovrebbe farti capire perché non ho fatto subito i calcoli, ma ho lasciato indicate le parentesi”.

“Sì, vedo. Comunque i calcoli li faccio: vediamo un po', questa volta il capitale alla fine dell'anno sarà uguale a 2.37 euro e rotti”.

“Sì, è aumentato rispetto a prima”.

“Ah, certo. Con questa faccenda dell'aumento dei periodi in cui si calcola l'interesse, possiamo diventare ricchi”.

“Siamo sicuri?”.

“Eh, bè, certo, accumuliamo denaro sempre di più, possiamo fare quello che vogliamo”.

“Facciamo una prova. Andiamo in banca ancora, e chiediamo se ci fanno il conto degli interessi ogni tre mesi, cioè quattro volte all'anno”.

“La formula dovrebbe essere questa:”.

“Sì, questa è quella finale. Se fai i conti, viene 2.44 e rotti”.

“È aumentato ancora”.

“Certo, questo è vero. Ma è aumentato di meno”.

“Insomma, o aumenta o non aumenta, no?”.

“Certo che aumenta, ma ci sono diversi modi di aumentare. Prova a chiedere alla banca se ti fa i conti una volta al mese, per esempio”.

“Sono dodici volte all'anno, dovrebbero essere tanti soldini. La formula è questa:”.

“Esatto. Risulta 2.613”.

“Uhm, mi aspettavo un aumento un po' più grosso”.

“Prova a sentire in banca se ti fanno il calcolo degli interessi una volta al giorno, allora”.

“Eh, magari. Vediamo, questo è il risultato:”.

“Bene, risulta 2.71457”.

“Comincio a capire: aumenta, ma aumenta sempre meno. Quanto ci metterà ad arrivare a 3?”.

“Forse in banca hanno tempo di farti i conti una volta ogni ora”.

“Ogni ora? Sarebbero 8760 calcoli all'anno!”.

“Che problema c'è? In banca hanno i computer, ci pensano loro a tenere il tuo conto aggiornato”.

“Ah, va bene. La formula diventa:”.

“E il risultato è 2.71813”.

“Niente, ancora non ci siamo. Faccio il calcolo una volta al minuto, allora. Ecco qua:”.

“Ancora troppo poco: risulta 2.71828”.

“Una volta al secondo! Sono preso dal sacro furore del ragioniere! Ecco qua:”.

“Purtoppo risulta 2.71828”.

“Come prima? Impossibile”.

“No, non proprio come prima: c'è stato un piccolo aumento nelle cifre che non ti ho detto, dopo la quinta decimale”.

“Ma allora quante volte devo calcolare gli interessi in un anno per avere il mio capitale triplicato?”.

“Il fatto è che non arriverai mai a 3. Il tuo capitale aumenta sempre, ma aumenta sempre di meno. Il risultato non si avvicina a 3, ma rimane minore”.

“Di quanto rimane minore? Cioè, a cosa si avvicina il risultato, alla fine?”.

“Il numero a cui si avvicina il tuo capitale, man mano che aumenti il numero di volte in cui fai il calcolo degli interessi, si avvicina a un numero irrazionale che i matematici indicano con e”.

“Una semplice e?”.

“Sì. La scrittura corretta che si usa è questa:”.

“lim?”.

“Sì, quel simbolo significa limite, ed è il modo matematico per dire quello che succede quando n diventa sempre più grande. Se tu chiedi alla banca di farti un calcolo degli interessi in ogni istante, o continuamente, il tuo capitale arriva fino a e, e non lo supera. Quindi questo non è un metodo per diventare ricchi”.

“Vabbè, già le ipotesi iniziali erano di pura fantasia, non esiste una banca che ti dà un interesse del cento per cento”.

“Non importa, io ho supposto un interesse del 100% per semplificare i calcoli, ma il numero e salta fuori anche se si fanno calcoli con dati reali”.

“Ah. Quindi è un numero molto importante?”.

“Eh, sì, ogni volta che si ha a che fare con fenomeni di accrescimento o decadimento, salta fuori e. Può trattarsi dell'accrescimento di un conto in banca, della crescita di una colonia batterica, del decadimento radioattivo, della scarica di un condensatore. Di esempi se ne possono fare tanti. Il numero e, detto anche numero di Nepero o di Eulero, è il numero più naturale che ci sia”.

Keplero era un nerd

A volte si ha l'impressione che esistano collegamenti nascosti tra ognuno di noi, che aspettano solo di essere portati alla luce. Questa è una di quelle volte.

Modena è terra di motori, di maiali, di buona cucina, di ciliegie, di parmigiano reggiano, di aceto balsamico. Parliamo dell'aceto.

La consorteria dell'aceto balsamico tradizionale di Modena nasce nel 1967 a Spilamberto, in provincia di Modena, grazie al fratello di mia nonna (io lo chiamavo zio). L'aceto matura all'interno di botti di legno, che la traduzione vuole fabbricate con legni degli antichi domini estensi (castagno, rovere, gelso, frassino, ciliegio e ginepro).

Io insegno in una scuola superiore che ha un indirizzo chimico: da qualche anno siamo in contatto con il consorzio dell'aceto balsamico allo scopo di far fare agli studenti analisi su campioni di aceto; dovremmo avviare, prima o poi, una nostra acetaia.

Siamo in periodo di esami, e gli studenti (almeno quelli un po' responsabili) stanno scrivendo le loro tesine d'esame. Uno di loro ha scelto come argomento proprio l'aceto balsamico. Uno dei suoi prof di chimica gli ha dato un libro che parla in modo approfondito della gestione di una acetaia; così approfondito che, pur non essendo un libro di matematica, il testo riesce a citare anche il calcolo integrale, a proposito del calcolo del volume di una botte. Lo studente ha chiesto lumi al prof di chimica, il quale l'ha mandato da me.

Il libro dice che per calcolare il volume di una botte si può usare il calcolo integrale, utilizzando la formula che permette di trovare il volume di un solido di rotazione: il calcolo non è difficile, ma il libro non è stato scritto da un matematico, e alcune definizioni vanno un po' interpretate.

Il libro elenca due casi: le doghe potrebbero essere curvate secondo un profilo parabolico, e in questo caso l'integrale si risolve abbastanza facilmente. Con un po' di calcoli abbiamo ricostruito tutti i passaggi mancanti nel libro, e verificato la formula indicata. Poi siamo passati al secondo caso: le doghe potrebbero essere curvate secondo un profilo circolare. In questo caso si ottengono dei calcoli complicatissimi: ci si riesce, ma la formula risultante è lunghissima, e comunque non è quella riportata dal libro (per chi vuole provare: il problema è dovuto al fatto che il centro della circonferenza che contiene le doghe non sta sull'asse della botte).

Allora mi sono messo a cercare un po' in giro, e ho pensato che probabilmente il libro dello studente faceva un errore: chiamava circonferenza ciò che, in effetti, era un'ellisse. Se si rifanno i calcoli con un profilo ellittico (ellisse con centro sull'asse della botte, questa volta) allora risulta una formulina semplice che dovrebbe essere quella riportata dal libro (appena rivedo lo studente, verifico).

Il bello di tutto ciò, però, è la storia che sta dietro al calcolo del volume di una botte. E questa storia ci porta a Keplero. Di lui Goethe ha scritto: quando si confronta la storia della vita di Keplero con ciò che egli è diventato e con ciò che ha ottenuto, si rimane allo stesso tempo felicemente stupiti e convinti del fatto che il vero genio è in grado di superare ogni ostacolo. Il destino è stato crudele con il nostro astronomo: dovette sopportare povertà, privazioni, malattie, e la morte delle persone care. Si sposò il 27 aprile 1597 con Barbara Müller, dalla quale ebbe cinque figli, i primi due morti nella prima infanzia. Nel 1611 gli altri tre figli contrassero il vaiolo, e uno di loro morì. Poco dopo morì anche la moglie.

Trasferitosi a Linz, in Austria, conobbe quella che sarebbe presto diventata la sua seconda moglie, Susanna Reuttinger. Nell'autunno del 1613 ci fu un raccolto molto favorevole di uva, grazie al quale il vino venne venduto a prezzo modico. Keplero ne ordinò alcune botti in vista dell'imminente festa di nozze, botti che vennero subito recapitate a casa sua. Quattro giorni dopo il venditore gli fece visita, e misurò il volume di ognuna di esse. Keplero rimase sconcertato: il venditore utilizzava un regolo di rame che infilava nell'apertura superiore di ogni botte, lo faceva scendere obliquamente fino a toccare il fondo, e misurava così la capacità, senza tener conto minimamente della forma dei contenitori.

Subito dopo il matrimonio, Keplero decise di inaugurare un nuovo campo di studio: le leggi geometriche che regolano il calcolo dei volumi, allo scopo di chiarirne le basi (se queste basi esistono). E fu così che vennero gettate le fondamenta del calcolo differenziale e integrale.

Lo studio dei volumi delle botti si concretizzò poi nel libro Nova stereometria doliorum vinariorum, pubblicato nel 1615; nel teorema V della seconda parte, si legge il seguente teorema: fra tutti i cilindri aventi la stessa diagonale, quello avente capacità maggiore è quello per il quale il rapporto tra il diametro di base e l'altezza è uguale alla radice di due.

Le botti austriache non erano proprio cilindriche, ma grosso modo avevano le dimensioni giuste (al contrario di quelle tedesche, più sottili e più alte). Perciò, concluse Keplero, il venditore di vino austriaco non l'aveva imbrogliato, perché la forma delle sue botti era quasi giusta. Quel quasi non dava troppo fastidio, perché vicino a un massimo i decrementi, da ambo i lati, sono praticamente impercettibili.

Alla faccia di Newton e Leibniz.

Dalla mela agli spaghetti

Un pomeriggio di tanti anni fa il signor Newton se ne stava tranquillo sotto a un melo a farsi una pennichella. A un certo punto una mela gli cadde sulla testa, svegliandolo di soprassalto.

“Ma tu guarda”, si disse Isacco un po' contrariato, “la mela si è diretta verso la mia testa, ma anche la terra si è diretta verso la mela. E io ci sono proprio in mezzo”. Questa, in termini non del tutto rigorosi, è stata la prima formulazione della legge di gravitazione universale, che afferma che tra due corpi si manifesta sempre una forza proporzionale alle loro masse e inversamente proporzionale al quadrato della loro distanza.

“Mo'c lavòr”, pensò Newton, che era di origine modenese da parte di madre, “questa faccenda dell'inverso del quadrato mi pare singolare. Chissà perché proprio il quadrato. E se fosse un due virgola qualcosina? O un uno e novantanove e rotti?”. Ma dato che i fisici son fisici, e non possono dimostrare niente, Newton si limitò a congetturare che le cose stessero così e provò a tirare qualche conseguenza.

“Vemmò, Galileo non è stato mica tanto preciso”, capì ben presto Isacco, “lui pensava che i corpi in caduta libera descrivessero delle parabole, invece no, sono ellissi”. Isacco però era uno onesto, e non voleva mica denigrare Galileo. Aveva capito che la descrizione del moto parabolico di Galileo era una approssimazione, dovuta all'aver immaginato la terra piatta e la forza di gravità perpendicolare al terreno. In effetti distinguere una parabola da un'ellisse non è mica tanto facile, bisognerebbe poter vedere fino all'infinito: l'ellisse prima o poi si chiude, la parabola non si chiude mai (neanche l'iperbole, ma lasciamo stare).

“Ma allora”, continuò ragionando Isacco, “se io, per dire, mi metto a correre molto veloce, ma molto molto veloce, potrei a un certo punto raggiungere una velocità che mi permette di orbitare intorno alla terra. E in quel caso disegnerei una bella ellisse. O, come caso particolare, una circonferenza. Se vado fortissimo, a un certo punto la mia ellisse non si chiuderà più, e avrò una parabola. Se vado a canna, una iperbole”. Newton era uno preciso.

“E in questo mio orbitare intorno alla terra, io sarei come in una continua caduta libera, e non sentirei più il mio peso. Togo!”. Si faceva anche molti viaggi mentali, bisogna dire.

“Però, un momento… Questa faccenda dell'inverso del quadrato non mi convince. Cioè, mettiamo che io corra veloce e mi metta in orbita intorno alla terra. Mettiamo anche che i miei piedi siano diretti verso il centro della terra, e la linea che congiunge la mia testa coi miei piedi passi sempre per quel centro. Io non sono mica un oggetto puntiforme, come dicono sempre i filosofi naturali”. Che erano poi i fisici, ma si facevano belli chiamandosi così.

Newton si mise allora a fare dei calcoli. Una persona che orbita intorno alla terra si trova sì in continua caduta libera, e non sente la forza di gravità, però i suoi piedi e la sua testa sono a distanze diverse dal centro della terra. Quindi, volendo essere pignoli, la forza esercitata sui piedi è diversa da quella esercitata sulla testa. Volendo essere molto pignoli, quella persona dovrebbe sentire questa differenza tra le due forze come un leggero allungamento.

Facciamo un po' di conti.

Supponiamo che la persona orbiti a una distanza dal centro della terra pari a quella a cui si trova la stazione spaziale internazionale: circa 6700 chilometri (distanza pari al raggio della terra più 350 chilometri). Supponiamo che questa persona sia alta 165 centimetri e pesi 65 chilogrammi (ogni battuta sui diversamente alti sarà cestinata senza pietà).

La differenza tra la forza applicata ai suoi piedi e quella applicata alla sua testa sarà dell'ordine di pochi decimillesimi di Newton. Naturalmente Newton non chiamava Newton l'unità di misura della forza, ma capiva anche lui che questa differenza era trascurabile.

“Bene”, concluse Isacco, “possiamo classificare queste pignolerie con il termine tecnico che noi filosofi naturali modenesi utilizziamo di solito in questi casi: menate. Andiamo avanti”. E passò a calcolare lo stesso tipo di forza utilizzando due corpi diversi: la terra e il sole. E scoprì così la forza di marea.

Lasciamo passare un po' di tempo, e arriviamo al 1976, dove incontriamo un altro scienziato: anche lui di nome Isaac, ma di cognome faceva Asimov. Asimov è stato un professore universitario di biochimica, ed è quindi corretto considerarlo un uomo di scienza. Tutti però lo conoscono come scrittore di fantascienza.

King Armstrong, editor della rivista Bell Telephone, durante un pranzo di lavoro gli domandò di scrivere un racconto di fantascienza che parlasse del futuro delle telecomunicazioni. Asimov rispose che avrebbe trovato una trama adatta prima della fine del pasto, e così fu. La storia si intitola Old Fashioned (Sistema antiquato, in italiano) e racconta di due minatori spaziali che si trovano ad orbitare intorno ad un buco nero non segnato sulle carte. Il vero protagonista della storia è l'effetto marea che, questa volta, non è trascurabile come nel caso del sistema astronauta-terra.

Già, questa volta l'effetto marea è notevole, dato che un buco nero è un oggetto molto diverso dalla terra: la sua densità è molto più alta. Ora, dato che un buco nero nessuno l'ha mai visto, proviamo a fare i calcoli con un oggetto un po' meno esotico: una stella di neutroni. Queste stelle hanno un diametro dell'ordine della decina di chilometri, ma una massa simile a quella del Sole. Questo significa che una ipotetica astronave (che supponiamo schermata da ogni tipo di radiazione letale) può orbitarle molto vicino, più di quanto potrebbe fare con il Sole, per esempio. E in questo caso l'inverso del quadrato si fa sentire: mentre nel caso della stazione spaziale internazionale orbitante intorno alla terra le distanze erano dell'ordine delle migliaia di chilometri, qua parliamo di decine o centinaia di chilometri. Elevando al quadrato, le differenze si amplificano ulteriormente (se la distanza si dimezza, la forza di marea diventa otto volte più grande). Se proviamo a fare i calcoli, scopriamo che ora la forza di marea esercitata sull'astronauta potrebbe facilmente arrivare alle centinaia di migliaia di Newton. Gli astronauti del bel racconto di Asimov sono ancora a distanza di sicurezza, nel senso che sono ancora vivi, ma l'astronave è danneggiata; non vado oltre per non rovinare la lettura; se avete voglia di leggere il racconto, si trova nell'Antologia del Bicentenario.

Arriviamo infine a un altro scienzato, l'ultimo della nostra storia: Stephen Hawking. Nel suo libro del 1988, A Brief History of Time, descrivendo la triste sorte di un astronauta che si avvicina troppo all'orizzonte degli eventi di un buco nero conia un nuovo termine, che è molto chiaro ed evocativo: spaghettification.

I fisici saranno anche un po' approssimativi in matematica, ma nessuno li supera quando si tratta di trovare nomi appropriati.

Ne hanno fatta un'altra

Motore a reazione a basa di coca e mentos.

Arnold

È morto Vladimir Igorevič Arnol'd, per gli amici Arnold. I non matematici probabilmente non l'hanno mai sentito nominare, ma era un matematico d'eccezione.

All'età di diciannove anni ha risolto il tredicesimo problema di Hilbert, a ventidue anni si è laureato e ha iniziato a lavorare presso l'università statale di Mosca, e da allora non ha mai smesso di fare il matematico.

Chi ha odiato l'esame di meccanica razionale, all'università, probabilmente non ha avuto la fortuna di avere un insegnante che seguiva il testo di Arnold: un testo stranissimo, con poche formule, tantissimi legami con la geometria, facile e difficile allo stesso tempo — il linguaggio molto chiaro e discorsivo lasciava spesso al lettore il compito di formalizzare e mettere in forma rigorosa alcuni passaggi. Io ho odiato l'insegnante, ho odiato il libro, ma quando è stata ora di prepararmi all'esame ho cambiato idea, e mi sono appassionato tanto che, come ultimo esame del corso di laurea, ho scelto meccanica superiore. Il programma di quell'esame si poteva riassumere in un solo, breve, titolo: il teorema KAM.

Eravamo in quattro o cinque a seguire il corso. Abbiamo passato circa sei-sette mesi di studio, di preparazione, di sviluppo della teoria necessaria per arrivare a capire il testo e la dimostrazione di un unico teorema, chiamato KAM dalle iniziali dei tre matematici che lo hanno scoperto inizialmente: Kolmogorov, Arnold e Moser. Bellissimo.

Il 10 settembre 1991 l'università di Bologna gli ha conferito la laurea honoris causa in matematica: io c'ero. Non ricordo assolutamente quale fosse l'argomento del suo discorso di ringraziamento, ma ricordo che fece cenno a una mappa caotica da lui scoperta: una funzione sul toro bidimensionale invertibile, che preserva l'area, con un insieme denso di punti periodici, ergodica, mixing, strutturalmente stabile, detta la mappa del gatto di Arnold. Sì, per spiegare il funzionamento di questo oggetto matematico Arnold metteva, nei suoi libri, il disegnino di un gatto (che veniva stirato, allungato, arrotolato su una ciambella, e strapazzato in tanti altri modi che non farebbero piacere agli amanti dei gatti).