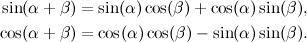Per completare il post precedente sulla legge dei grandi numeri e il gioco di testa o croce, ecco perché la differenza tra numero di teste e numero di croci varia come la radice del numero di lanci.
Indichiamo con T(n) il numero di teste dopo n lanci, e con C(n) il numero di croci. La differenza D(n) è naturalmente uguale a T(n)-C(n).
Ogni volta che n aumenta di 1, il valore di D(n) o aumenta di 1 oppure diminuisce di 1, cioè:
D(n+1) = D(n)+1 oppure D(n+1) = D(n)-1.
Elevando al quadrato, si ottiene
D(n+1)2 = D(n)2 + 1 ± 2D(n).
E qui mi sono piantato, perché mi avevano spiegato una cosa di cui non ero convinto, sono rimasto lì a rimuginarci sopra per un po' di tempo, fino a che non ho capito che mi ponevo la domanda sbagliata. Come si dice, spesso la risposta a una domanda è la stessa domanda formulata meglio.
Ecco come stanno le cose: dalla formula scritta sopra vorrei passare al valor medio di D. Questo significa che devo immaginare di fare tante sequenze di lanci (virtualmente tutte le sequenze di lanci) e calcolare la media dei termini presenti nell'uguaglianza scritta qua sopra. Io pensavo invece di fare la media al variare di n, sbagliando.
Se quindi facciamo la media su tutte le possibili sequenze di testa o croce, otteniamo che il valor medio di
D(n+1)2 è uguale al valor medio di D(n)2 + 1, perché il valor medio di D(n) è zero. Infatti, per ogni sequenza di teste e croci esiste la sequenza gemella ottenuta scambiando di posto le teste con le croci, e quindi per ogni D(n) positivo esiste un D(n) negativo che annulla la somma. Ragionando invece su una singola sequenza di lanci, è chiaro che non possiamo dire molto su D(n), ogni sequenza fa quello che vuole e avrà una media di D(n) diversa.
Ma allora, se il valor medio di D(n+1)2 è uguale al valor medio di D(n)2 + 1, questo significa che il valore medio del quadrato di D(n) aumenta ogni volta di 1, e dopo n lanci vale quindi esattamente n.
E dunque la radice del valore medio di D(n)2, che si chiama scarto quadratico medio, è proprio la radice di n. Ecco fatto.
Concludo con un aneddoto finale: Enrico Fermi, dopo avere perso una partita a tennis a Los Alamos per 6-4 contro un matematico, gli disse che l'altro non poteva dire di avere vinto perché lo scarto era inferiore alla radice di n, con n = 6+4 = 10.
lunedì 24 ottobre 2011
venerdì 21 ottobre 2011
Sulla legge dei grandi numeri e problemi affini
Volevo spiegare agli studenti il fatto che due infiniti dello stesso ordine possono avere rapporto finito ma non differenza finita, e volevo farlo in modo che il concetto rimanesse ben impresso nella memoria.
Allora ho fatto l'esempio del gioco del testa-o-croce: se lancio una moneta, la probabilità che esca testa è uguale a 1/2, ed è uguale alla probabilità che esca croce. Se io eseguo il lancio molte volte, mi aspetto che il rapporto tra numero di teste e numero di croci si avvicini sempre di più a 1 (se la moneta non è truccata, naturalmente). Questo è, in sostanza, quello che dice la legge dei grandi numeri (la quale ha una formulazione più sottile: la convergenza a 1 del rapporto è una convergenza in probabilità, cioè il rapporto converge al valore teorico con probabilità 1 (e probabilità 1 non significa che avverrà certamente, ma che avverrà quasi certamente (sì, i Veri Matematici hanno dato un significato rigoroso anche al quasi, roba da matti))).
Ora vediamo l'inghippo: analizziamo una serie di lanci e scopriamo che testa è uscita per 42000 volte. Cosa deduciamo? La prima risposta è questa: anche il numero di croci sarà molto vicino a 42000.
Bene, questo è sbagliato. Si può dimostrare che la differenza tra teste e croci non rimane costante, ma varia come la radice quadrata del numero di lanci. Se ho fatto quindi circa 100000 lanci, posso aspettarmi una differenza anche di circa 300. D'accordo, 300 è piccolo rispetto a 100000, ma non importa: il fatto è che questo valore cresce sempre, e tende ad infinito.
Insomma, se noi vediamo che ci sono 300 teste in più e deduciamo che le croci sono ritardatarie, e che certamente prima o poi ne usciranno molte, sbagliamo clamorosamente.
Ora si può anche fare l'esempio algebrico: le due successioni N+√N e N hanno rapporto che tende a 1 e differenza che tende a infinito.
Ho poi portato gli studenti in laboratorio, e ho fatto scrivere agli increduli un programmino che simulasse il lancio di una moneta, in modo da verificare la teoria. Il fatto è che alcuni sono invece riusciti a falsificarla.
Confortato dalla certezza che i teoremi matematici non sono falsificabili, sono andato a cercare l'errore, e dopo un po' di ricerche ho capito cosa era successo.
Per simulare il lancio di una moneta, alcuni avevano utilizzato la seguente istruzione C:
che comporta le seguenti operazioni: crea un numero casuale con la funzione rand(), numero che è un intero compreso tra 0 e un valore massimo memorizzato all'interno della costante RAND_MAX, e guarda se è pari o dispari. Se è pari è uscita testa, se è dispari invece croce (o viceversa, non importa).
Bisogna ricordare che le funzioni che generano numeri casuali utilizzate dai vari linguaggi di programmazione non generano numeri davvero casuali: non c'è un omino, dentro al programma, che lancia un dado ogni volta che c'è bisogno. Ci sono invece delle funzioni matematiche che simulano la casualità, utilizzando tecniche diverse. Una delle più diffuse è quella che fa uso di un sistema che si chiama generatore lineare congruenziale, molto semplice da implementare, ma anche un po' scarsino. Sotto alcune condizioni, i bit meno significativi dei numeri pseudo-casuali generati con questo sistema hanno un periodo molto breve, e controllare se un numero è pari oppure dispari significa proprio utilizzare il bit meno significativo dell'intera sequenza. E quindi l'esperimento fallisce, perché le teste e le croci si presentano con preoccupante periodicità.
Come si fa allora a generare numeri casuali buoni?
In questo caso, l'istruzione che ho riportato qua sopra va sostituita da quest'altra:
che significa
Così funziona bene.
Il compilatore usato a scuola è il Dev C++, che evidentemente usa, nella sua funzione rand(), questo sistema poco affidabile. Ho controllato quello che succede nel gcc, e ho trovato che la libreria C presente sul mio sistema non presenta questo problema. Il manuale, però, dice che non si può essere sicuri del fatto che rand() funzioni bene su ogni implementazione di questa funzione.
Per essere sicuri, invece, del fatto che anche i bit meno significativi siano sufficientemente casuali, occorre usare un'altra funzione, che si chiama random().
Ecco allora un programmino che lancia una moneta 50000 volte e salva su file i risultati:
Il programma scrive su un file quattro colonne: nella prima c'è il rapporto teste/croci, nella seconda la differenza teste-croci, nelle ultime due i valori di più o meno la radice del numero dei lanci. Il tutto serve per produrre queso grafico:
La curva rossa è il rapporto teste/croci: si stabilizza rapidamente verso il valore 1 (tanto che sembra una retta orizzontale, ma non lo è). La curva blu, invece, è la differenza tra teste e croci: come si vede non si stabilizza per niente, anzi, oscilla molto e il suo andamento è compreso all'interno della parabola viola (non necessariamente all'interno: la variabilità della curva blu è dello stesso ordine di quella della parabola, cioè di più o meno radice del numero di lanci).
Allora ho fatto l'esempio del gioco del testa-o-croce: se lancio una moneta, la probabilità che esca testa è uguale a 1/2, ed è uguale alla probabilità che esca croce. Se io eseguo il lancio molte volte, mi aspetto che il rapporto tra numero di teste e numero di croci si avvicini sempre di più a 1 (se la moneta non è truccata, naturalmente). Questo è, in sostanza, quello che dice la legge dei grandi numeri (la quale ha una formulazione più sottile: la convergenza a 1 del rapporto è una convergenza in probabilità, cioè il rapporto converge al valore teorico con probabilità 1 (e probabilità 1 non significa che avverrà certamente, ma che avverrà quasi certamente (sì, i Veri Matematici hanno dato un significato rigoroso anche al quasi, roba da matti))).
Ora vediamo l'inghippo: analizziamo una serie di lanci e scopriamo che testa è uscita per 42000 volte. Cosa deduciamo? La prima risposta è questa: anche il numero di croci sarà molto vicino a 42000.
Bene, questo è sbagliato. Si può dimostrare che la differenza tra teste e croci non rimane costante, ma varia come la radice quadrata del numero di lanci. Se ho fatto quindi circa 100000 lanci, posso aspettarmi una differenza anche di circa 300. D'accordo, 300 è piccolo rispetto a 100000, ma non importa: il fatto è che questo valore cresce sempre, e tende ad infinito.
Insomma, se noi vediamo che ci sono 300 teste in più e deduciamo che le croci sono ritardatarie, e che certamente prima o poi ne usciranno molte, sbagliamo clamorosamente.
Ora si può anche fare l'esempio algebrico: le due successioni N+√N e N hanno rapporto che tende a 1 e differenza che tende a infinito.
Ho poi portato gli studenti in laboratorio, e ho fatto scrivere agli increduli un programmino che simulasse il lancio di una moneta, in modo da verificare la teoria. Il fatto è che alcuni sono invece riusciti a falsificarla.
Confortato dalla certezza che i teoremi matematici non sono falsificabili, sono andato a cercare l'errore, e dopo un po' di ricerche ho capito cosa era successo.
Per simulare il lancio di una moneta, alcuni avevano utilizzato la seguente istruzione C:
if (rand() % 2) == 1
che comporta le seguenti operazioni: crea un numero casuale con la funzione rand(), numero che è un intero compreso tra 0 e un valore massimo memorizzato all'interno della costante RAND_MAX, e guarda se è pari o dispari. Se è pari è uscita testa, se è dispari invece croce (o viceversa, non importa).
Bisogna ricordare che le funzioni che generano numeri casuali utilizzate dai vari linguaggi di programmazione non generano numeri davvero casuali: non c'è un omino, dentro al programma, che lancia un dado ogni volta che c'è bisogno. Ci sono invece delle funzioni matematiche che simulano la casualità, utilizzando tecniche diverse. Una delle più diffuse è quella che fa uso di un sistema che si chiama generatore lineare congruenziale, molto semplice da implementare, ma anche un po' scarsino. Sotto alcune condizioni, i bit meno significativi dei numeri pseudo-casuali generati con questo sistema hanno un periodo molto breve, e controllare se un numero è pari oppure dispari significa proprio utilizzare il bit meno significativo dell'intera sequenza. E quindi l'esperimento fallisce, perché le teste e le croci si presentano con preoccupante periodicità.
Come si fa allora a generare numeri casuali buoni?
In questo caso, l'istruzione che ho riportato qua sopra va sostituita da quest'altra:
if ((float) rand()/RAND_MAX) < 0.5
che significa
- genera un numero casuale intero compreso tra 0 e RAND_MAX,
- trasformalo in un numero float (con la virgola, insomma),
- dividilo per RAND_MAX, ottenendo così un numero compreso tra 0 e 1,
- se è minore di 0.5 è uscita testa, altrimenti croce.
Così funziona bene.
Il compilatore usato a scuola è il Dev C++, che evidentemente usa, nella sua funzione rand(), questo sistema poco affidabile. Ho controllato quello che succede nel gcc, e ho trovato che la libreria C presente sul mio sistema non presenta questo problema. Il manuale, però, dice che non si può essere sicuri del fatto che rand() funzioni bene su ogni implementazione di questa funzione.
Per essere sicuri, invece, del fatto che anche i bit meno significativi siano sufficientemente casuali, occorre usare un'altra funzione, che si chiama random().
Ecco allora un programmino che lancia una moneta 50000 volte e salva su file i risultati:
#define NUM 50000
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<math.h>
/* viene usata la funzione random() al posto di rand() perche' usa
un generatore di numeri casuali migliore. In vecche implementazioni
di rand(), ad esempio, i bit meno significativi hanno un periodo
molto breve, per cui non si puo' usare rand()%2 per estrarre un
numero compreso tra 0 e 1
*/
int main(void)
{
int i,t=0,c=0;
FILE *f=fopen("grandinumeri.csv","wt");
srandom((unsigned)time(NULL));
for (i=0;i<NUM;i++) {
if ((float) random()/RAND_MAX < 0.5) {
t++;
}
else {
c++;
}
if (c!=0) { // salto i primi calcoli fino a che non ho almeno una c
fprintf(f,"%f, %d, %f, %f\n",(float)t/c,t-c,sqrt(i),-sqrt(i));
}
}
fclose(f);
}
Il programma scrive su un file quattro colonne: nella prima c'è il rapporto teste/croci, nella seconda la differenza teste-croci, nelle ultime due i valori di più o meno la radice del numero dei lanci. Il tutto serve per produrre queso grafico:
La curva rossa è il rapporto teste/croci: si stabilizza rapidamente verso il valore 1 (tanto che sembra una retta orizzontale, ma non lo è). La curva blu, invece, è la differenza tra teste e croci: come si vede non si stabilizza per niente, anzi, oscilla molto e il suo andamento è compreso all'interno della parabola viola (non necessariamente all'interno: la variabilità della curva blu è dello stesso ordine di quella della parabola, cioè di più o meno radice del numero di lanci).
giovedì 20 ottobre 2011
giovedì 13 ottobre 2011
In onore di Ritchie
#define _ -F<00||--F-OO--;
int F=00,OO=00;main(){F_OO();printf("%1.3f\n",4.*-F/OO/OO);}F_OO()
{
_-_-_-_
_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_
_-_-_-_
}
Un programma in K&R C che calcola il valore di pi greco analizzando la propria area.
(
Se lo si vuole compilare su sistemi moderni, occorre questo comando:
gcc -traditional-cpp -o r r.c
)
Dimostrazione senza parole: sin(α+β)
Ne ho trovata un'altra:
L'area del parallelogramma di sinistra (quello bianco) è uguale a sin(α+β), ed è anche uguale alla somma delle aree dei due rettangoli bianchi di destra, cioè sin(α)cos(β)+cos(α)sin(β).
L'area del parallelogramma di sinistra (quello bianco) è uguale a sin(α+β), ed è anche uguale alla somma delle aree dei due rettangoli bianchi di destra, cioè sin(α)cos(β)+cos(α)sin(β).
sabato 8 ottobre 2011
Martin Gardner — The Colossal Book of Mathematics
Se siete interessati agli articoli di Martin Gardner e non avete voglia di recuperare in giro tutti i suoi libri, potete risparmiare un po' di fatica con questo:
Martin Gardner, The Colossal Book of Mathematics, Norton, 25.74 euro.
Si tratta della raccolta dei pezzi più popolari scritti da Martin per la rubrica Mathematical Games di Scientific American: 736 pagine di arte della divulgazione matematica.
Gli articoli sono divisi per argomento: troviamo una prima parte sulla teoria dei numeri, seguita dall'algebra, la geometria, la probabilità, la topologia, la teoria dei giochi, l'infinito, il calcolo combinatorio, la fisica, la logica, la filosofia e altro ancora. Ci sono i flexagoni, il gioco Life, i polimini… insomma, c'è di tutto.
Per motivi che diventeranno chiari tra qualche giorno segnalo in particolare il capitolo 5, intitolato Rep-Tiles: un gioco di parole intraducibile, perché i reptiles sono i rettili, ma anche le tessere (tiles) che vengono replicate.
In pratica i rep-tiles sono poligoni formati da pezzi uguali tra loro e, possibilmente, aventi la stessa forma del poligono originale. Tipo questo:
Se siete appassionati di matematica ricreativa, questa roba è da leggere.
Martin Gardner, The Colossal Book of Mathematics, Norton, 25.74 euro.
Si tratta della raccolta dei pezzi più popolari scritti da Martin per la rubrica Mathematical Games di Scientific American: 736 pagine di arte della divulgazione matematica.
Gli articoli sono divisi per argomento: troviamo una prima parte sulla teoria dei numeri, seguita dall'algebra, la geometria, la probabilità, la topologia, la teoria dei giochi, l'infinito, il calcolo combinatorio, la fisica, la logica, la filosofia e altro ancora. Ci sono i flexagoni, il gioco Life, i polimini… insomma, c'è di tutto.
Per motivi che diventeranno chiari tra qualche giorno segnalo in particolare il capitolo 5, intitolato Rep-Tiles: un gioco di parole intraducibile, perché i reptiles sono i rettili, ma anche le tessere (tiles) che vengono replicate.
In pratica i rep-tiles sono poligoni formati da pezzi uguali tra loro e, possibilmente, aventi la stessa forma del poligono originale. Tipo questo:
Se siete appassionati di matematica ricreativa, questa roba è da leggere.
mercoledì 5 ottobre 2011
Questo è il titolo di questa storia, che si trova anche parecchie volte nella storia stessa
Questa è la prima frase di questa storia. Questa è la seconda frase. Questo è il titolo di questa storia, che si trova anche parecchie volte nella storia stessa. Questa frase si interroga sul valore intrinseco delle prime due frasi. Questa frase vi informa, nel caso non ve ne foste già accorti, che questa è una storia autoreferenziale, cioè una storia formata da frasi che si riferiscono alla loro propria struttura e funzione. Questa è una frase che serve per finire il primo capoverso.
Questa è la prima frase di un nuovo capoverso di una storia autoreferenziale. Questa frase vi fa conoscere il protagonista della storia, un ragazzo di nome Billy. Questa frase vi dice che Billy è biondo, con gli occhi azzurri, americano, ha 12 anni e strangola sua madre. Questa frase fa un commento sulla goffa natura della forma narrativa autoreferenziale mentre riconosce lo strano e divertente distacco che garantisce allo scrittore. Come per illustrare quanto detto nell'ultima frase, questa frase ci ricorda, senza ombra di facezia, che i bambini sono un prezioso dono divino e che il mondo è un posto migliore quando è benedetto dalle gioie e delizie che essi vi portano.
Questa frase descrive gli occhi della madre di Billy che schizzano fuori dalle orbite e la sua lingua che penzola e fa riferimento agli spiacevoli gorgoglii che sta emettendo. Questa frase fa l'osservazione che questi sono tempi incerti e difficili e che i rapporti, anche quelli apparentemente permanenti e profondamente radicati, hanno la tendenza a rompersi.
Introduce in questo capoverso l'espediente dei frammenti di frase. Un frammento di frase. Un altro. Buon espediente. Sarà più usato in seguito.
Questa è in realtà l'ultima frase della storia, ma è stata messa qui per sbaglio. Questo è il titolo di questa storia, che si trova anche parecchie volte nella storia stessa. Svegliatosi una mattina uscendo da sgradevoli sogni, Gregor Samsa si trovò nel suo letto trasformato in un gigantesco insetto. Questa frase vi informa che la frase precedente è di un'altra storia (una molto migliore, va detto) e non c'entra niente in questo passo della narrazione. A dispetto delle affermazioni della frase precedente, questa frase si sente obbligata a informarvi che la storia che state leggendo è in realtà "La metamorfosi", di Franz Kafka, e che la frase a cui ci si riferiva nella frase precedente è l'unica frase che appartiene davvero a questa storia. Questa frase annulla la frase precedente informando il lettore (povero, confuso infelice) che questo brano letterario è in realtà la Dichiarazione di indipendenza, ma che l'autore, in un gesto di estrema negligenza (se non di malizioso sabotaggio), non ha finora incluso nemmeno una sola frase di quel commovente documento, anche se ha accondisceso a usare un piccolo frammento di frase, vale a dire "quando nel corso degli umani eventi", chiuso tra virgolette vicino alla fine della frase. Mostrando una chiara consapevolezza della noia e della sincera ostilità del lettore medio verso gli inutili giochi concettuali a cui si indulgeva nelle frasi precedenti, questa frase ci riporta infine allo scenario della storia ponendo la domanda: "Perché Billy strangola sua madre?" Questa frase cerca di fare un po’ di luce sulla domanda posta dalla frase precedente, ma non ci riesce. Questa frase, invece, ci riesce suggerendo una possibile relazione incestuosa tra Billy e sua madre e alludendo alle concomitanti complicazioni freudiane che ogni lettore astuto vedrà immediatamente. Incesto. L'innominabile tabù. La proibizione universale. Incesto. E si notano i frammenti di frase? Buon espediente letterario. Sarà più usato in seguito.
Questa è la prima frase di un nuovo capoverso. Questa è l'ultima frase di un nuovo capoverso.
Questa frase può servire sia da inizio di un capoverso sia da fine, a seconda della sua posizione. Questo è il titolo di questa storia, che si trova anche parecchie volte nella storia stessa. Questa frase solleva una seria obiezione verso l'intera classe di frasi autoreferenziali che si limitano a commentare la propria funzione o la propria posizione all'interno della storia (ad esempio le ultime quattro frasi), per il fatto che esse sono monotonamente prevedibili, indimenticabilmente autoindulgenti e servono semplicemente a distrarre il lettore dal vero argomento di questa storia, che a questo punto sembra avere a che fare con strangolamento e incesto e chissà quali altre delizie. Lo scopo di questa frase è rilevare che la frase precedente, anche se non appartiene essa stessa alla classe di frasi autoreferenziali contro cui solleva obiezioni, nondimeno serve anch'essa semplicemente a distrarre il lettore dal vero argomento di questa storia, che in realtà ha a che fare con l'inesplicabile trasformazione di Gregor Samsa in un insetto gigantesco (a dispetto delle rumorose affermazioni contrarie di altre benintenzionate, ma male informate frasi). Questa frase può servire sia da inizio di un capoverso sia da fine, a seconda della sua posizione.
Questo è il titolo di questa storia, che si trova anche parecchie volte nella storia stessa. Questo è quasi il titolo di questa storia, che si trova solo una volta nella storia stessa. Questa frase afferma a malincuore che fino a questo punto il modo narrativo autoreferenziale ha avuto un effetto paralizzante sul progresso della storia stessa, cioè queste frasi sono state talmente impegnate ad analizzare se stesse e il loro ruolo nella storia che hanno finito per non compiere la loro funzione di comunicatori di eventi e idee che uno spera si fondano in una trama, in uno sviluppo dei personaggi, ecc., in breve, la vera raison d'étre di ogni rispettabile frase all'interno di un brano di irresistibile prosa. Questa frase rileva inoltre l'ovvia analogia tra la condizione di queste agonizzanti frasi autocoscienti e le analoghe afflizioni degli esseri umani, e sottolinea gli analoghi effetti paralizzanti che scaturiscono da un'eccessiva e torturata autoanalisi.
Lo scopo di questa frase (che può anche servire da capoverso) è di riflettere che se la Dichiarazione di indipendenza fosse stata formulata e strutturata allo stesso modo lezioso e incoerente di questa storia, non si potrebbe dire in che tipo di corrotta società libertina vivremmo ora o in quali abissi di decadenza potrebbero essere precipitati gli abitanti di questo paese, fino al punto che scrittori squilibrati e degradati costruiscano frasi irritantemente ingombranti e inutilmente prolisse che a volte possiedono la discutibile se non del tutto indesiderabile proprietà di riferirsi a se stesse ed esse a volte arrivano a divenire frasi sconclusionate o mostrano altri segni di inescusabile sciatteria grammaticale quali non necessarie ridondanze superflue che quasi certamente avrebbero insidiosi effetti sullo stile di vita e sulla morale della nostra impressionabile gioventù, portandola a commettere incesto o addirittura assassinio e forse è per questo che Billy sta strangolando sua madre, a causa di frasi proprio come questa, che non hanno obiettivi discernibili o scopi perspicui e terminano in un punto qualsiasi, anche in mez
Bizzarro. Un frammento di frase. Un altro frammento. Dodici anni. Questa è una frase che. Frammentata. E strangolando sua madre. Scusate, scusate. Bizzarro. Questo. Più frammenti. Questo è. Frammenti. Il titolo di questa storia, che. Biondo. Scusate, scusate. Frammento dopo frammento. Più difficile. Questa è una frase che. Frammenti. Diavolo buon espediente.
Lo scopo di questa frase è triplice: (1) scusarsi per la sfortunata e inesplicabile scorrettezza nel capoverso precedente; (2) assicurarti, lettore, che non accadrà più; e (3) ripetere l'affermazione che questi sono tempi incerti e difficili e che aspetti del linguaggio, anche quelli apparentemente stabili e profondamente radicati come la sintassi e il significato, si spezzano. Questa frase non aggiunge nulla di sostanziale a ciò che è stato espresso nella frase precedente, ma serve semplicemente da frase conclusiva per questo capoverso, che altrimenti potrebbe non averne una.
Questa frase, in un improvviso e coraggioso soprassalto di altruismo, cerca di abbandonare il modo autoreferenziale, ma fallisce. Questa frase cerca di nuovo, ma il tentativo è condannato in partenza.
Questa frase, in un ultimo e disperato tentativo di infondere un minimo di narrazione in questa prosa paralizzata, allude rapidamente ai frenetici tentativi di Billy di nascondersi, seguita da un lirico, toccante e bel passaggio in cui Billy si riconcilia con suo padre (risolvendo così i subliminali conflitti freudiani che risultano ovvi a qualsiasi astuto lettore) e da un’eccitante scena finale di caccia da parte della polizia durante la quale Billy è accidentalmente colpito e ucciso da una recluta della polizia in preda al panico che per coincidenza si chiama anch'essa Billy. Questa frase, anche se fondamentalmente in completa simpatia con i lodevoli sforzi dell'ultima frase densa d'azione, ricorda al lettore che queste allusioni a una storia che in realtà non esiste ancora non sono in alcun modo sostituti della cosa reale e pertanto non possono tirar fuori l'autore (quello stupido indolente) dalla proverbiale trappola.
Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso.
Lo scopo. Di questo capoverso. È di scusarsi. Per l'uso gratuito. Di. Frammenti di frase. Scusate.
Lo scopo di questa frase è scusarsi per gli inutili e sciocchi giochetti da adolescenti a cui si indulgeva nei due precedenti capoverso, ed esprimere da parte di noi, le frasi più mature, il rincrescimento per il fatto che, nel complesso, il tono di questa storia è tale da non riuscire a comunicare un semplice, per quanto un po' torbido, scenario.
Questa frase desidera scusarsi per le inutili scuse che si trovano in questa storia (questa inclusa), che, anche se manifestamente qui poste a beneficio dei lettori più irritati, non fanno che ritardare in modo esasperantemente ripetitivo la prosecuzione dell'ormai quasi dimenticata linea narrativa.
Questa frase mette l'accento sul terribile significato dell'autoriferimento applicato alle frasi, una pratica che potrebbe dimostrarsi un vero vaso di Pandora di potenziale rovina, in quanto se una frase può riferirsi o alludere a se stessa, perché non un'umile proposizione subordinata, magari proprio questa? O questo frammento di frase? O tre parole? Due parole? Una?
Forse è giusto che questa frase ci ricordi gentilmente e senza ombra di condiscendenza che questi sono davvero tempi difficili e incerti e che in genere le persone non sono buone l'una con l'altra, e che forse noi, esseri umani senzienti o frasi senzienti che siamo, dovremmo sforzarci di più. Voglio dire che c'è qualcosa come il libero arbitrio, ci deve essere, e questa frase ne è la prova! Nè questa frase nè tu, lettore, siete completamente senza speranza davanti alle impietose forze che operano nell'universo. Dovremmo stare ben piantati per terra, affrontare i fatti, prendere Madre Natura per il collo e sforzarci di più. Per la gola. Di più. Di più, di più.
Scusate.
Questo è il titolo di questa storia, che si trova anche parecchie volte nella storia stessa.
Questa è l'ultima frase della storia. Questa è l'ultima frase della storia. Questa è l'ultima frase della storia. Questa è. Scusate.
(David Moser, riportato da Hofstadter sulla rubrica Temi Metamagici di un Le Scienze di tanti anni fa)
Questa è la prima frase di un nuovo capoverso di una storia autoreferenziale. Questa frase vi fa conoscere il protagonista della storia, un ragazzo di nome Billy. Questa frase vi dice che Billy è biondo, con gli occhi azzurri, americano, ha 12 anni e strangola sua madre. Questa frase fa un commento sulla goffa natura della forma narrativa autoreferenziale mentre riconosce lo strano e divertente distacco che garantisce allo scrittore. Come per illustrare quanto detto nell'ultima frase, questa frase ci ricorda, senza ombra di facezia, che i bambini sono un prezioso dono divino e che il mondo è un posto migliore quando è benedetto dalle gioie e delizie che essi vi portano.
Questa frase descrive gli occhi della madre di Billy che schizzano fuori dalle orbite e la sua lingua che penzola e fa riferimento agli spiacevoli gorgoglii che sta emettendo. Questa frase fa l'osservazione che questi sono tempi incerti e difficili e che i rapporti, anche quelli apparentemente permanenti e profondamente radicati, hanno la tendenza a rompersi.
Introduce in questo capoverso l'espediente dei frammenti di frase. Un frammento di frase. Un altro. Buon espediente. Sarà più usato in seguito.
Questa è in realtà l'ultima frase della storia, ma è stata messa qui per sbaglio. Questo è il titolo di questa storia, che si trova anche parecchie volte nella storia stessa. Svegliatosi una mattina uscendo da sgradevoli sogni, Gregor Samsa si trovò nel suo letto trasformato in un gigantesco insetto. Questa frase vi informa che la frase precedente è di un'altra storia (una molto migliore, va detto) e non c'entra niente in questo passo della narrazione. A dispetto delle affermazioni della frase precedente, questa frase si sente obbligata a informarvi che la storia che state leggendo è in realtà "La metamorfosi", di Franz Kafka, e che la frase a cui ci si riferiva nella frase precedente è l'unica frase che appartiene davvero a questa storia. Questa frase annulla la frase precedente informando il lettore (povero, confuso infelice) che questo brano letterario è in realtà la Dichiarazione di indipendenza, ma che l'autore, in un gesto di estrema negligenza (se non di malizioso sabotaggio), non ha finora incluso nemmeno una sola frase di quel commovente documento, anche se ha accondisceso a usare un piccolo frammento di frase, vale a dire "quando nel corso degli umani eventi", chiuso tra virgolette vicino alla fine della frase. Mostrando una chiara consapevolezza della noia e della sincera ostilità del lettore medio verso gli inutili giochi concettuali a cui si indulgeva nelle frasi precedenti, questa frase ci riporta infine allo scenario della storia ponendo la domanda: "Perché Billy strangola sua madre?" Questa frase cerca di fare un po’ di luce sulla domanda posta dalla frase precedente, ma non ci riesce. Questa frase, invece, ci riesce suggerendo una possibile relazione incestuosa tra Billy e sua madre e alludendo alle concomitanti complicazioni freudiane che ogni lettore astuto vedrà immediatamente. Incesto. L'innominabile tabù. La proibizione universale. Incesto. E si notano i frammenti di frase? Buon espediente letterario. Sarà più usato in seguito.
Questa è la prima frase di un nuovo capoverso. Questa è l'ultima frase di un nuovo capoverso.
Questa frase può servire sia da inizio di un capoverso sia da fine, a seconda della sua posizione. Questo è il titolo di questa storia, che si trova anche parecchie volte nella storia stessa. Questa frase solleva una seria obiezione verso l'intera classe di frasi autoreferenziali che si limitano a commentare la propria funzione o la propria posizione all'interno della storia (ad esempio le ultime quattro frasi), per il fatto che esse sono monotonamente prevedibili, indimenticabilmente autoindulgenti e servono semplicemente a distrarre il lettore dal vero argomento di questa storia, che a questo punto sembra avere a che fare con strangolamento e incesto e chissà quali altre delizie. Lo scopo di questa frase è rilevare che la frase precedente, anche se non appartiene essa stessa alla classe di frasi autoreferenziali contro cui solleva obiezioni, nondimeno serve anch'essa semplicemente a distrarre il lettore dal vero argomento di questa storia, che in realtà ha a che fare con l'inesplicabile trasformazione di Gregor Samsa in un insetto gigantesco (a dispetto delle rumorose affermazioni contrarie di altre benintenzionate, ma male informate frasi). Questa frase può servire sia da inizio di un capoverso sia da fine, a seconda della sua posizione.
Questo è il titolo di questa storia, che si trova anche parecchie volte nella storia stessa. Questo è quasi il titolo di questa storia, che si trova solo una volta nella storia stessa. Questa frase afferma a malincuore che fino a questo punto il modo narrativo autoreferenziale ha avuto un effetto paralizzante sul progresso della storia stessa, cioè queste frasi sono state talmente impegnate ad analizzare se stesse e il loro ruolo nella storia che hanno finito per non compiere la loro funzione di comunicatori di eventi e idee che uno spera si fondano in una trama, in uno sviluppo dei personaggi, ecc., in breve, la vera raison d'étre di ogni rispettabile frase all'interno di un brano di irresistibile prosa. Questa frase rileva inoltre l'ovvia analogia tra la condizione di queste agonizzanti frasi autocoscienti e le analoghe afflizioni degli esseri umani, e sottolinea gli analoghi effetti paralizzanti che scaturiscono da un'eccessiva e torturata autoanalisi.
Lo scopo di questa frase (che può anche servire da capoverso) è di riflettere che se la Dichiarazione di indipendenza fosse stata formulata e strutturata allo stesso modo lezioso e incoerente di questa storia, non si potrebbe dire in che tipo di corrotta società libertina vivremmo ora o in quali abissi di decadenza potrebbero essere precipitati gli abitanti di questo paese, fino al punto che scrittori squilibrati e degradati costruiscano frasi irritantemente ingombranti e inutilmente prolisse che a volte possiedono la discutibile se non del tutto indesiderabile proprietà di riferirsi a se stesse ed esse a volte arrivano a divenire frasi sconclusionate o mostrano altri segni di inescusabile sciatteria grammaticale quali non necessarie ridondanze superflue che quasi certamente avrebbero insidiosi effetti sullo stile di vita e sulla morale della nostra impressionabile gioventù, portandola a commettere incesto o addirittura assassinio e forse è per questo che Billy sta strangolando sua madre, a causa di frasi proprio come questa, che non hanno obiettivi discernibili o scopi perspicui e terminano in un punto qualsiasi, anche in mez
Bizzarro. Un frammento di frase. Un altro frammento. Dodici anni. Questa è una frase che. Frammentata. E strangolando sua madre. Scusate, scusate. Bizzarro. Questo. Più frammenti. Questo è. Frammenti. Il titolo di questa storia, che. Biondo. Scusate, scusate. Frammento dopo frammento. Più difficile. Questa è una frase che. Frammenti. Diavolo buon espediente.
Lo scopo di questa frase è triplice: (1) scusarsi per la sfortunata e inesplicabile scorrettezza nel capoverso precedente; (2) assicurarti, lettore, che non accadrà più; e (3) ripetere l'affermazione che questi sono tempi incerti e difficili e che aspetti del linguaggio, anche quelli apparentemente stabili e profondamente radicati come la sintassi e il significato, si spezzano. Questa frase non aggiunge nulla di sostanziale a ciò che è stato espresso nella frase precedente, ma serve semplicemente da frase conclusiva per questo capoverso, che altrimenti potrebbe non averne una.
Questa frase, in un improvviso e coraggioso soprassalto di altruismo, cerca di abbandonare il modo autoreferenziale, ma fallisce. Questa frase cerca di nuovo, ma il tentativo è condannato in partenza.
Questa frase, in un ultimo e disperato tentativo di infondere un minimo di narrazione in questa prosa paralizzata, allude rapidamente ai frenetici tentativi di Billy di nascondersi, seguita da un lirico, toccante e bel passaggio in cui Billy si riconcilia con suo padre (risolvendo così i subliminali conflitti freudiani che risultano ovvi a qualsiasi astuto lettore) e da un’eccitante scena finale di caccia da parte della polizia durante la quale Billy è accidentalmente colpito e ucciso da una recluta della polizia in preda al panico che per coincidenza si chiama anch'essa Billy. Questa frase, anche se fondamentalmente in completa simpatia con i lodevoli sforzi dell'ultima frase densa d'azione, ricorda al lettore che queste allusioni a una storia che in realtà non esiste ancora non sono in alcun modo sostituti della cosa reale e pertanto non possono tirar fuori l'autore (quello stupido indolente) dalla proverbiale trappola.
Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso. Capoverso.
Lo scopo. Di questo capoverso. È di scusarsi. Per l'uso gratuito. Di. Frammenti di frase. Scusate.
Lo scopo di questa frase è scusarsi per gli inutili e sciocchi giochetti da adolescenti a cui si indulgeva nei due precedenti capoverso, ed esprimere da parte di noi, le frasi più mature, il rincrescimento per il fatto che, nel complesso, il tono di questa storia è tale da non riuscire a comunicare un semplice, per quanto un po' torbido, scenario.
Questa frase desidera scusarsi per le inutili scuse che si trovano in questa storia (questa inclusa), che, anche se manifestamente qui poste a beneficio dei lettori più irritati, non fanno che ritardare in modo esasperantemente ripetitivo la prosecuzione dell'ormai quasi dimenticata linea narrativa.
Questa frase mette l'accento sul terribile significato dell'autoriferimento applicato alle frasi, una pratica che potrebbe dimostrarsi un vero vaso di Pandora di potenziale rovina, in quanto se una frase può riferirsi o alludere a se stessa, perché non un'umile proposizione subordinata, magari proprio questa? O questo frammento di frase? O tre parole? Due parole? Una?
Forse è giusto che questa frase ci ricordi gentilmente e senza ombra di condiscendenza che questi sono davvero tempi difficili e incerti e che in genere le persone non sono buone l'una con l'altra, e che forse noi, esseri umani senzienti o frasi senzienti che siamo, dovremmo sforzarci di più. Voglio dire che c'è qualcosa come il libero arbitrio, ci deve essere, e questa frase ne è la prova! Nè questa frase nè tu, lettore, siete completamente senza speranza davanti alle impietose forze che operano nell'universo. Dovremmo stare ben piantati per terra, affrontare i fatti, prendere Madre Natura per il collo e sforzarci di più. Per la gola. Di più. Di più, di più.
Scusate.
Questo è il titolo di questa storia, che si trova anche parecchie volte nella storia stessa.
Questa è l'ultima frase della storia. Questa è l'ultima frase della storia. Questa è l'ultima frase della storia. Questa è. Scusate.
(David Moser, riportato da Hofstadter sulla rubrica Temi Metamagici di un Le Scienze di tanti anni fa)
martedì 4 ottobre 2011
lunedì 3 ottobre 2011
Sostiene Bollani
Ieri sera, durante la terza puntata, ha eseguito 4'33" di John Cage. Non ce n'è più per nessuno.
Iscriviti a:
Commenti (Atom)