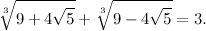Our whole universe was in a hot dense state

Le (più di cento) immagini che compongo la sigla iniziale di The Big Bang Theory.

Criteri di divisibilità (quasi) senza parole

Un numero è divisibile per 2 se la sua ultima cifra è divisibile per 2. E fin qua.

Complichiamo le cose con un disegnino. Scriviamo uno 0 e un 1, mettiamo un dito sullo 0, e cominciamo a contare da 0 al numero di cui vogliamo stabilire la divisibilità per 2, spostando il dito alternativamente sullo 0 e sull'1 che abbiamo scritto. Se finiamo la conta sullo 0, il numero è divisibile per 2, altrimenti non lo è.

Possiamo fare la stessa cosa per quanto riguarda la divisibilità per ogni numero: se vogliamo vedere se un numero è divisibile per 3, ad esempio, dobbiamo scrivere i numeri 0, 1 e 2 e contare, come se essi fossero collegati in maniera circolare, così:

Però, se il numero che stiamo studiando è molto grande, la faccenda diventa noiosa. Prendiamo un numero a caso, ad esempio 42. Se non vogliamo fare il giro dell'oca per 42 volte, possiamo scomporlo in decine e unità. Abbiamo 4 decine: dato che 3 decine sono certamente divisibili per 3, è come se avessimo una sola decina da considerare. E sappiamo che 10 è uguale a 9+1, quindi dopo aver contato per 40 passi dobbiamo finire sul numero 1. Poi aggiungiamo le 2 unità e arriviamo sullo 0: 42 è divisibile per 3. Bella forza.

La morale della storia è che invece di contare 42 volte si potrebbe contare solo 4 volte per le decine, 2 volte per le unità, e si ottiene il risultato corretto: il passaggio da decine a unità è come se non ci fosse. Ma perché succede questo? Funziona sempre così?

Proviamo ad analizzare quello che succede. Una decina, abbiamo detto, è uguale a 9+1, quindi fare 10 passi corrisponde a farne uno solo. Contare dunque le decine o le unità è la stessa cosa. Possiamo passare da decine a unità come se niente fosse, o anche da centinaia a decine, o da migliaia a centinaia, eccetera.

Vediamo che succede con 2 decine: dato che 20 è uguale a 18+2, contare 2 decine oppure contare 2 unità è uguale. Stessa cosa con 30: 30 è multiplo di 10 e quindi contare per 30 passi è come stare fermi sullo zero.

Potremmo allora generalizzare il nostro schema in questo modo: mettiamo il dito sullo 0, consideriamo la prima cifra del numero dato e cominciamo a contare. Ogni volta che cambiamo cifra (passando da decine a unità, o a centinaia a decine, o da migliaia a centinaia, eccetera) dobbiamo seguire una freccia rossa.

Ok, direte, è una cosa un po' inutile. È vero.

Proviamo a fare lo schema per il criterio di divisibilità per 4.

Qui le cose cambiano un po': 10, ad esempio, è uguale a 8+2, quindi se passiamo da una decina alle unità, dobbiamo saltare da 1 a 2. Invece 20 è un multiplo di 4, quindi quando passiamo da 2 decine alle unità, ripartiamo da 0. Infine, 30 è uguale a 28+2, quindi passando da 3 decine alle unità ripartiamo da 2.

La regola dunque è questa: conto sulle cifre nere, quando cambio posizione seguo una freccia rossa, poi ricomincio.

Ecco la divisibilità per 5 (questo è facile, le decine sono tutte divisibili per 5).

Il grafo per il criterio di divisibilità per 6 comincia a diventare interessante:

Ora arriviamo a un bel numero primo: 7

Tra l'altro, esiste un criterio di divisibilità per 7, ma è un po' complicato. Funziona in questo modo: dal numero dato si cancella l'ultima cifra e si sottrae dal risultato il doppio della cifra appena cancellata, e si va avanti così fino a che non si capisce se il numero ottenuto è multiplo di sette oppure no.

In formule:

x → x div 10 - 2(x mod 10)

Esempio: partiamo da 325 → 32 - 2×5 = 22, non divisibile per 7.
Altro esempio: partiamo da 294 → 29 - 2×4 = 21, divisibile per 7.

Esercizio: riuscite a dimostrare che il grafo della divisibilità per 7 è planare (cioè sta sul piano senza che vi siano intersezioni tra le varie frecce)? Qui la soluzione.

Dicono poi che il grafo per la divisibilità per 8 non sia planare, ma non conosco la dimostrazione. Comunque eccolo qua:

Ecco il 9:

(la prova del 9 ce la ricordiamo, no?).

Infine (saltando il grafo per il 10), ecco quello per la divisibilità per 11:

La disposizione dei numeri in queste figure è stata fatta da un programma, graphviz — io ho soltanto dovuto scrivere i vari collegamenti, ci ha pensato lui a dare una forma circolare al tutto. Se trovate dei modi migliori per rappresentare i vari criteri, fatemi sapere.

Ah, dimenticavo un ultimo grafo:

Non era una bugia

Quando, più di due mesi fa, ho parlato di Scienza Express, avevo detto che non ci avrei guadagnato niente nel farlo. Ed era proprio così. L'ho fatto perché si parlava di libri scientifici, perché mi piaceva l'idea di libri disponibili nel tempo, perché c'era un occhio di riguardo per gli insegnanti.

Poi mi sono detto: ehi, ma anche io sono un insegnante. E, ora che ci penso, anche io ho scritto una specie di libro, che è stato pubblicato su questo blog, che parlava di scienza (di matematica, per la precisione).

Allora ho riscritto ai due signori di Scienza Express e ho domandato: ma lo sapete che anche io ho scritto delle cose che forse vi possono piacere? Non è che magari vi interessano?

Bè, mi han detto sì.

Battlestar Galactica space and timeline

Se, durante la visione di Battlestar Galactica (e magari di Caprica) vi siete un po' persi, e ancora vi chiedete quante volte sono stati creati i cyloni, ecco una meravigliosa space and timeline.

(cliccare per ingrandire)

Poi dicono che la fisica è utile

In un tavolo da biliardo perfettamente piano le palle rotolano al centro.

Cose inutili