“Ehi, guarda, ho scoperto un generatore di numeri primi!”.
“Uhm”.
“Come uhm? Guarda:”.
P(n) = n2 + n + 41
“Uhm”.
“Ma insomma, cosa c'è che non va? P(0) fa 41, che è un numero primo”.
“Questo è vero”.
“P(1) fa 43, che è ancora primo”.
“Vero anche questo”.
“P(2) fa 47, P(3) fa 53, tutti primi”.
“Certo”.
“E posso andare avanti così, i numeri successivi sono 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281, 313, 347, 383, 421, 461, 503, 547, 593, 641, 691, 743, 797, 853, 911, 971, 1033”.
“Molto bene”.
“Quindi sto generando numeri primi”.
“Sì, certo. Hai calcolato P(41)?”.
“Aspetta che faccio i calcoli”.
“Forse non hai bisogno di fare tutti i conti per dire se è primo o no”.
“Perché?”.
“Beh, stai sommando tre numeri: 412 + 41 + 41”.
“Oh”.
“Come vedi, 41 è un fattore comune a tutti e tre”.
“Uffa, risulta un numero composto”.
“Sì, 41 × 43. Prova anche a calcolare P(40)”.
“Questo sarà primo, dai”.
“Prova”.
“Allora: 402 + 40 + 41”.
“Che, volendo, puoi scrivere come 402 + 80 + 1”.
“E perché questa scrittura dovrebbe essere meglio?”.
“Perché è uguale a (40 + 1)2, cioè 412”.
“Oh, è composto anche questo”.
“Già”.
“Ma ci sarà un polinomio che funziona, no?”.
“Cioè un polinomio P(n) a coefficienti interi in una variabile n che assuma valori primi per ogni n intero positivo?”.
“Uh, mamma mia, che pignoleria. Sì, un polinomio fatto così”.
“Certo, eccotene uno: P(n) = 2”.
“Eh? Ma no, che genera numeri primi diversi!”.
“Allora lo vuoi anche non costante”.
“Sì! Quanto sono noiosi questi Veri Matematici”.
“Capisci che bisogna esser precisi, altrimenti poi non si sa bene quello che si vuole”.
“Va bene, va bene. Esiste un polinomio così?”.
“No”.
“Ma come? Tra tutti gli infiniti polinomi che si possono costruire, non ce n'è nemmeno uno che genera solo numeri primi?”.
“Nemmeno uno”.
“Santo cielo. E perché?”.
“Immagina che ne esista uno, per esempio uno che assuma il valore 43 quando n = 1”.
“Come fa il mio”.
“Esatto: possiamo scrivere che P(1) = 43”.
“Bene”.
“Ora prova a calcolare P(1 + 43k)”.
“Cos'è k?”.
“Un qualunque numero intero”.
“Eh, ma come faccio a calcolare P(1 + 43k) se non so come sia fatto P?”.
“Allora, partiamo dall'inizio. Supponiamo che esista P, che sarà scritto in maniera molto generica in questo modo:”.
P(n) = anxn + an−1xn−1 + … + a1x + a0
“Gulp”.
“Prova a calcolare, adesso, P(1 + 43k)”.
“Vediamo, risulterà una cosa del genere:”.
P(1 + 43k) = an(1 + 43k)n + an−1(1 + 43k)n−1 + … + a1(1 + 43k) + a0
“Bene. Comincia a svolgere”.
“Stai scherzando?”.
“No, ma non devi svolgere tutto tutto. Per esempio, da tutte quelle parentesi del tipo (1 + 43k) elevate a una qualche potenza puoi estrarre il primo termine, che è 1”.
“Eh, ma poi c'è un sacco di altra roba”.
“Certo, cominciamo dal facile: ognuna di quelle parentesi genera sicuramente un 1”.
“Va bene. Ognuno di quegli 1 viene moltiplicato per un coefficiente diverso”.
“E quindi puoi cominciare a scrivere una cosa del genere:”.
P(1 + 43k) = an + an−1 + … + a1 + a0 + (altra roba)
“Non mi sembra una scrittura molto matematica, però va bene”.
“Ti ricordi quanto faceva P(1)?”.
“Abbiamo detto 43”.
“E, però, se sostituisci 1 nel tuo generico polinomio cosa ottieni?”.
“Ah, facile, ottengo an + an−1 + … + a1 + a0”.
“Benissimo. Quindi sai che an + an−1 + … + a1 + a0 = 43”.
“Ah. Ma allora posso scrivere così:”.
P(1 + 43k) = 43 + (altra roba)
“Certo. Adesso concentriamoci sull'altra roba”.
“E come facciamo? Dobbiamo svolgere tutte quelle potenze di binomio, non si finisce più”.
“Non facciamolo. Sarai d'accordo con me se ti dico che lo sviluppo di qualunque potenza del tipo (1 + 43k)n contiene un termine uguale a 1, e tanti altri termini che contengono, almeno una volta, il fattore 43?”.
“Eh, sì, giusto. Tutti i termini dopo il primo 1 contengono le varie potenze di 43k. Non ricordo bene il calcolo dei coefficienti, però”.
“Beh, non importa ai fini dei calcoli che stiamo facendo. Senza conoscere nessuna regola, puoi immaginare di dover calcolare quella potenza in questo modo:”.
(1 + 43k)n = (1 + 43k)(1 + 43k) … (1 + 43k)
“Ah, certo”.
“Quando ti calcoli tutti i prodotti, vedi che c'è un solo caso in cui fai 1×1×…×1, mentre in tutti gli altri casi almeno un termine del tipo 43k lo devi prendere”.
“Giusto, e quindi un 43 c'è sempre”.
“Ottimo. Ed ecco allora che possiamo semplificare ulteriormente il calcolo che stavamo facendo, mettendo in evidenza il fattore comune 43:”.
P(1 + 43k) = 43 + 43(altra roba ancora)
“Bene, e quindi?”.
“E quindi P(1 + 43k) è divisibile per 43”.
“E allora?”.
“E allora non è primo, dunque P(n) non può assumere valori primi per ogni valore di n”.
“Ah!”.
“Volendo essere più precisi, bisognerebbe distinguere due casi nell'espressione P(1 + 43k) = 43 + 43(altra roba ancora)”.
“Quali?”.
“Se la parentesi (altra roba ancora) fosse uguale a 0, allora il risultato sarebbe 43, che è effettivamente un numero primo”.
“Allora potrebbe succedere?”.
“Eh, questo significherebbe che P(1 + 43k) dovrebbe essere uguale a 43 per infiniti valori di k”.
“E questo non è possibile?”.
“Lo è, ma un polinomio che assume infiniti valori uguali è un polinomio costante”.
“Ah, il caso banale P(n) = 43”.
“Già. Se vuoi un polinomio non costante e in grado di generare solo numeri primi, non ce la fai. Non esiste. Naturalmente 43 è solo un esempio, puoi rifare tutta la dimostrazione sostituendo, al posto di 43, un qualsiasi numero p primo. Quindi, niente da fare: non esiste un polinomio P(n) non costante a coefficienti interi in una variabile n che assuma valori primi per ogni n intero positivo”.
“Oh. Peccato”.
“Già”.
mercoledì 26 dicembre 2018
giovedì 6 dicembre 2018
Minacce aliene — Parte 4
“Bene, quindi il problema diventa: se ciascuno dei numeri da 1 a n viene colorato di rosso o di blu, qual è il minimo valore di n per ottenere una progressione aritmetica monocromatica composta da 3, oppure 4, oppure k termini?”.
“Oh, due variabili?”.
“Eh, le cose si complicano”.
“Già mi pare un ottimo risultato affermare che un valore di n che risolve il problema esiste sempre”.
“E hai ragione, questo è il primo passo notevole. Dopo aver dimostrato l’esistenza di un tale n, van der Waerden ha provato anche a stabilirne un valore minimo. Il fatto è che questo valore minimo è enorme, così grande da non poter essere espresso nelle usuali notazioni a cui siamo abituati”.
“Eh? Come è possibile? La notazione scientifica permette di esprimere numeri enormi”.
“Che però sono ridicolmente piccoli se confrontati col numero trovato da van Der Waerden”.
“Incredibile”.
“Per definire il numero ha usato una successione di funzioni, che crescono sempre più velocemente”.
“Uhm, non capisco”.
“Aspetta, partiamo dal semplice. Non avrai difficoltà a immaginare la funzione DOPPIO(x), che raddoppia il suo ingresso”.
“Stai dicendo che DOPPIO(x) = 2x?”.
“Esatto”.
“E c’è bisogno di una funzione apposita?”.
“Per calcolare il doppio, certamente no. Per capire come è fatta la nostra successione di funzioni, invece, sì. Lasciami andare avanti”.
“Ok, vai”.
“Ora definisco la funzione ESPONENTE(x), che calcola il valore di 2 elevato a esponente x”.
“Una funzione esponenziale”.
“Sì, la cosa interessante è che questa funzione è definibile a partire da DOPPIO(x)”.
“In che modo?”.
“Cosa succede se calcoli per x volte il doppio di 1?”.
“Aspetta, allora… se calcolo 1 volta il doppio di 1, ottengo 2, e fin qua è facile. Se calcolo 2 volte il doppio di 1, ottengo 2 per 2, cioè 4. Se calcolo 3 volte il doppio di 1, ottengo 2 per 2 per 2… ah! Certo, se calcolo x volte il doppio di 1, ottengo 2 elevato a x, cioè ESPONENTE(x)”.
“Quindi possiamo dire che ESPONENTE(x) = DOPPIO(DOPPIO(...DOPPIO(1))), dove la funzione DOPPIO compare x volte”.
“Bello, comincio a capire”.
“Ora facciamo un altro passo, definiamo la funzione TORRE(x)”.
“Che immagino sia fatta dall'applicazione di x volte della funzione ESPONENTE”.
“Infatti.”.
“Da dove viene il nome TORRE?”.
“Prova a calcolare TORRE(3)”.
“Vediamo, TORRE(3) = ESPONENTE(ESPONENTE(ESPONENTE(1)))”.
“Ok, quindi partiamo da ESPONENTE(1)”.
“ESPONENTE(1) = DOPPIO(1), no?”.
“Certo”.
“E DOPPIO(1) = 2”.
“Giusto anche questo. Quindi TORRE(3) = ESPONENTE(ESPONENTE(2))”.
“Bene, allora adesso devo calcolare ESPONENTE(2), che è uguale a DOPPIO(DOPPIO(1)), cioè DOPPIO(2), cioè 4”.
“Infatti avevamo visto che ESPONENTE(2) calcola 2 elevato a 2, cioè 4”.
“Ah, ecco, vero. Quindi mi rimane da calcolare ESPONENTE(4)”.
“Si capisce meglio se calcoli ESPONENTE(22), applicando direttamente l’esponenziale”.
“Applicando direttamente la definizione di ESPONENTE, verrebbe 222”.
“”Una torre di potenze. Ecco perché questa funzione si chiama TORRE: calcola torri di potenze.
“Non è come fare una potenza di una potenza?”.
“Eh, no, qui non ci sono parentesi: per calcolare una torre di potenze, si parte dall'alto. Per esempio, TORRE(4) è 2222 = 224 = 216, mentre ((22)2)2, che è la cosiddetta potenza di potenza, è uguale a 28.
“Ok, ci sono”.
“Ora andiamo avanti, definiamo una nuova funzione, WOW(x). Ti anticipo che WOW non ha nessun significato se non quello di stupore, per quanto veloce cresce questa funzione”.
“Non ci posso credere”.
“Eh, in mancanza di nomi migliori… I numeri calcolati da WOW sono enormi. Naturalmente, WOW(x) è definita come TORRE(TORRE(…TORRE(1))), dove la funzione TORRE compare x volte”.
“Gulp. Chissà quanto vale WOW(4)”.
“Un numero enorme. WOW(4) = TORRE(TORRE(TORRE(TORRE(1))))”.
“Uhm, TORRE(1) è uguale a 2, fin qua è facile. Quindi mi rimane da calcolare TORRE(TORRE(TORRE(2)))”.
“Anche TORRE(2) è facile, no?”.
“Certo, è uguale a 22, cioè 4”.
“Ok, quindi ora devi calcolare TORRE(TORRE(4))”.
“TORRE(4) è una torre di 2 composta da 4 elementi, cioè 2222, che è uguale a 65536”.
“Bene, ultimo passo, devi calcolare TORRE(65536)”.
“Argh”.
“O anche wow!”.
“Una torre di potenze composta da 65536 esponenti, una cosa impossibile da immaginare”.
“Esattamente”.
“E questo numero è quello trovato da van der Waerden?”.
“Oh, no, questo è ancora piccolo se confrontato con quello”.
“Cosa?”.
“Eh, sì. Per arrivare al numero trovato da van der Waerden, occorre immaginare questa successione di funzioni:”.
DOPPIO(1)
ESPONENTE(2)
TORRE(3)
WOW(4)
eccetera
“Ogni volta applichiamo tante volte la funzione precedente?”.
“Esattamente”.
“E dopo WOW che funzioni ci sono?”.
“Non sono stati definiti nomi per le funzioni successive. Sai come si fa, si definisce una regola e poi si va avanti così. Per scrivere i termini successivi si usa un nome generico, che è ACKERMANN”.
“Questo è un nome proprio, suppongo?”.
“Esatto, dal nome di chi l’ha definita. Una volta capito che a ogni passo si deve applicare la funzione precedente un certo numero di volte, possiamo definire la funzione ACKERMANN in questo modo:”.
ACKERMANN(1) = DOPPIO(1)
ACKERMANN(2) = ESPONENTE(2)
ACKERMANN(3) = TORRE(3)
ACKERMANN(4) = WOW(4)
eccetera
“Quell'eccetera fa paura”.
“Ed eccoci arrivati alla soluzione del problema proposto da van der Waerden”.
“Se ciascuno dei numeri da 1 a n viene colorato di rosso o di blu, qual è il minimo valore di n per ottenere una progressione aritmetica monocromatica composta da k termini?”.
“E la risposta è: ACKERMANN(k)”.
“Quindi, tornando al quesito iniziale, quello delle progressioni aritmetiche composte da 3 numeri dello stesso colore, siamo sicuri di trovarne se prendiamo i numeri che vanno da 1 a ACKERMANN(3), giusto?”.
“Giusto”.
“E ACKERMANN(3) è uguale a TORRE(3), cioè 16. Uhm, non avevo dimostrato che anche solo prendendo i numeri da 1 a 9 troverò sempre una progressione aritmetica monocolore?”.
“Sì, certo. La stima ACKERMANN(k) è una condizione sufficiente per essere sicuri di trovare la progressione monocolore. Non è detto che, con ulteriori studi, non si possa migliorare la stima. Anzi, un miglioramento è già stato fatto: nella dimostrazione originale di van der Waerden compare il numero ACKERMANN(k), ma successivamente, nel 1987, il matematico israeliano Sharon Shelah ha dimostrato che ci si può fermare a WOW(k)”.
“Ah, ecco. Rimane comunque un numero colossale”.
“E, per quanto riguarda il quesito iniziale, ancora più inutile: WOW(3) è uguale a 65536”.
“Se k aumenta, però, WOW(k) rimane a un livello inferiore rispetto a ACKERMANN(k), vero?”.
“Esatto. Sappi che Graham, un altro matematico che ha lavorato alla teoria di Ramsey, ha offerto un premio di 1000 dollari per chiunque sia in grado di dimostrare che, al posto di WOW(k), si può usare TORRE(k). O a chi sia in grado di dimostrare il contrario, cioè che TORRE(k) è un numero troppo basso”.
“Anche in questo campo, quindi, ci sono molti problemi aperti”.
“Già. Quella di Ramsey è una teoria affascinante, proprio perché si occupa di trovare strutture ordinate all'interno di strutture apparentemente casuali. Un articolo divulgativo di Graham e Spencer, comparso su Le Scienze nel 1990, si concludeva con questa domanda: oggi, grazie alla teoria di Ramsey, siamo in grado di riconoscere con facilità le costellazioni del cielo notturno. Quali configurazioni potremmo mai trovare in insiemi che sono ACKERMANN(9) volte più grandi?”.
“Speriamo di non trovare alieni cattivi, però”.
Questa è l'ultima parte di un articolo uscito sulla rivista Archimede, numero 4, del 2017. La prima parte è qua, la seconda qua, la terza qua.
“Oh, due variabili?”.
“Eh, le cose si complicano”.
“Già mi pare un ottimo risultato affermare che un valore di n che risolve il problema esiste sempre”.
“E hai ragione, questo è il primo passo notevole. Dopo aver dimostrato l’esistenza di un tale n, van der Waerden ha provato anche a stabilirne un valore minimo. Il fatto è che questo valore minimo è enorme, così grande da non poter essere espresso nelle usuali notazioni a cui siamo abituati”.
“Eh? Come è possibile? La notazione scientifica permette di esprimere numeri enormi”.
“Che però sono ridicolmente piccoli se confrontati col numero trovato da van Der Waerden”.
“Incredibile”.
“Per definire il numero ha usato una successione di funzioni, che crescono sempre più velocemente”.
“Uhm, non capisco”.
“Aspetta, partiamo dal semplice. Non avrai difficoltà a immaginare la funzione DOPPIO(x), che raddoppia il suo ingresso”.
“Stai dicendo che DOPPIO(x) = 2x?”.
“Esatto”.
“E c’è bisogno di una funzione apposita?”.
“Per calcolare il doppio, certamente no. Per capire come è fatta la nostra successione di funzioni, invece, sì. Lasciami andare avanti”.
“Ok, vai”.
“Ora definisco la funzione ESPONENTE(x), che calcola il valore di 2 elevato a esponente x”.
“Una funzione esponenziale”.
“Sì, la cosa interessante è che questa funzione è definibile a partire da DOPPIO(x)”.
“In che modo?”.
“Cosa succede se calcoli per x volte il doppio di 1?”.
“Aspetta, allora… se calcolo 1 volta il doppio di 1, ottengo 2, e fin qua è facile. Se calcolo 2 volte il doppio di 1, ottengo 2 per 2, cioè 4. Se calcolo 3 volte il doppio di 1, ottengo 2 per 2 per 2… ah! Certo, se calcolo x volte il doppio di 1, ottengo 2 elevato a x, cioè ESPONENTE(x)”.
“Quindi possiamo dire che ESPONENTE(x) = DOPPIO(DOPPIO(...DOPPIO(1))), dove la funzione DOPPIO compare x volte”.
“Bello, comincio a capire”.
“Ora facciamo un altro passo, definiamo la funzione TORRE(x)”.
“Che immagino sia fatta dall'applicazione di x volte della funzione ESPONENTE”.
“Infatti.”.
“Da dove viene il nome TORRE?”.
“Prova a calcolare TORRE(3)”.
“Vediamo, TORRE(3) = ESPONENTE(ESPONENTE(ESPONENTE(1)))”.
“Ok, quindi partiamo da ESPONENTE(1)”.
“ESPONENTE(1) = DOPPIO(1), no?”.
“Certo”.
“E DOPPIO(1) = 2”.
“Giusto anche questo. Quindi TORRE(3) = ESPONENTE(ESPONENTE(2))”.
“Bene, allora adesso devo calcolare ESPONENTE(2), che è uguale a DOPPIO(DOPPIO(1)), cioè DOPPIO(2), cioè 4”.
“Infatti avevamo visto che ESPONENTE(2) calcola 2 elevato a 2, cioè 4”.
“Ah, ecco, vero. Quindi mi rimane da calcolare ESPONENTE(4)”.
“Si capisce meglio se calcoli ESPONENTE(22), applicando direttamente l’esponenziale”.
“Applicando direttamente la definizione di ESPONENTE, verrebbe 222”.
“”Una torre di potenze. Ecco perché questa funzione si chiama TORRE: calcola torri di potenze.
“Non è come fare una potenza di una potenza?”.
“Eh, no, qui non ci sono parentesi: per calcolare una torre di potenze, si parte dall'alto. Per esempio, TORRE(4) è 2222 = 224 = 216, mentre ((22)2)2, che è la cosiddetta potenza di potenza, è uguale a 28.
“Ok, ci sono”.
“Ora andiamo avanti, definiamo una nuova funzione, WOW(x). Ti anticipo che WOW non ha nessun significato se non quello di stupore, per quanto veloce cresce questa funzione”.
“Non ci posso credere”.
“Eh, in mancanza di nomi migliori… I numeri calcolati da WOW sono enormi. Naturalmente, WOW(x) è definita come TORRE(TORRE(…TORRE(1))), dove la funzione TORRE compare x volte”.
“Gulp. Chissà quanto vale WOW(4)”.
“Un numero enorme. WOW(4) = TORRE(TORRE(TORRE(TORRE(1))))”.
“Uhm, TORRE(1) è uguale a 2, fin qua è facile. Quindi mi rimane da calcolare TORRE(TORRE(TORRE(2)))”.
“Anche TORRE(2) è facile, no?”.
“Certo, è uguale a 22, cioè 4”.
“Ok, quindi ora devi calcolare TORRE(TORRE(4))”.
“TORRE(4) è una torre di 2 composta da 4 elementi, cioè 2222, che è uguale a 65536”.
“Bene, ultimo passo, devi calcolare TORRE(65536)”.
“Argh”.
“O anche wow!”.
“Una torre di potenze composta da 65536 esponenti, una cosa impossibile da immaginare”.
“Esattamente”.
“E questo numero è quello trovato da van der Waerden?”.
“Oh, no, questo è ancora piccolo se confrontato con quello”.
“Cosa?”.
“Eh, sì. Per arrivare al numero trovato da van der Waerden, occorre immaginare questa successione di funzioni:”.
DOPPIO(1)
ESPONENTE(2)
TORRE(3)
WOW(4)
eccetera
“Ogni volta applichiamo tante volte la funzione precedente?”.
“Esattamente”.
“E dopo WOW che funzioni ci sono?”.
“Non sono stati definiti nomi per le funzioni successive. Sai come si fa, si definisce una regola e poi si va avanti così. Per scrivere i termini successivi si usa un nome generico, che è ACKERMANN”.
“Questo è un nome proprio, suppongo?”.
“Esatto, dal nome di chi l’ha definita. Una volta capito che a ogni passo si deve applicare la funzione precedente un certo numero di volte, possiamo definire la funzione ACKERMANN in questo modo:”.
ACKERMANN(1) = DOPPIO(1)
ACKERMANN(2) = ESPONENTE(2)
ACKERMANN(3) = TORRE(3)
ACKERMANN(4) = WOW(4)
eccetera
“Quell'eccetera fa paura”.
“Ed eccoci arrivati alla soluzione del problema proposto da van der Waerden”.
“Se ciascuno dei numeri da 1 a n viene colorato di rosso o di blu, qual è il minimo valore di n per ottenere una progressione aritmetica monocromatica composta da k termini?”.
“E la risposta è: ACKERMANN(k)”.
“Quindi, tornando al quesito iniziale, quello delle progressioni aritmetiche composte da 3 numeri dello stesso colore, siamo sicuri di trovarne se prendiamo i numeri che vanno da 1 a ACKERMANN(3), giusto?”.
“Giusto”.
“E ACKERMANN(3) è uguale a TORRE(3), cioè 16. Uhm, non avevo dimostrato che anche solo prendendo i numeri da 1 a 9 troverò sempre una progressione aritmetica monocolore?”.
“Sì, certo. La stima ACKERMANN(k) è una condizione sufficiente per essere sicuri di trovare la progressione monocolore. Non è detto che, con ulteriori studi, non si possa migliorare la stima. Anzi, un miglioramento è già stato fatto: nella dimostrazione originale di van der Waerden compare il numero ACKERMANN(k), ma successivamente, nel 1987, il matematico israeliano Sharon Shelah ha dimostrato che ci si può fermare a WOW(k)”.
“Ah, ecco. Rimane comunque un numero colossale”.
“E, per quanto riguarda il quesito iniziale, ancora più inutile: WOW(3) è uguale a 65536”.
“Se k aumenta, però, WOW(k) rimane a un livello inferiore rispetto a ACKERMANN(k), vero?”.
“Esatto. Sappi che Graham, un altro matematico che ha lavorato alla teoria di Ramsey, ha offerto un premio di 1000 dollari per chiunque sia in grado di dimostrare che, al posto di WOW(k), si può usare TORRE(k). O a chi sia in grado di dimostrare il contrario, cioè che TORRE(k) è un numero troppo basso”.
“Anche in questo campo, quindi, ci sono molti problemi aperti”.
“Già. Quella di Ramsey è una teoria affascinante, proprio perché si occupa di trovare strutture ordinate all'interno di strutture apparentemente casuali. Un articolo divulgativo di Graham e Spencer, comparso su Le Scienze nel 1990, si concludeva con questa domanda: oggi, grazie alla teoria di Ramsey, siamo in grado di riconoscere con facilità le costellazioni del cielo notturno. Quali configurazioni potremmo mai trovare in insiemi che sono ACKERMANN(9) volte più grandi?”.
“Speriamo di non trovare alieni cattivi, però”.
Questa è l'ultima parte di un articolo uscito sulla rivista Archimede, numero 4, del 2017. La prima parte è qua, la seconda qua, la terza qua.
venerdì 9 novembre 2018
Minacce aliene — Parte 3
“Come disse il matematico Theodore Motzkin descrivendo la teoria di Ramsey: complete disorder is impossible”.
“Uh, chissà cosa ne pensano i filosofi”.
“Eh, non è un’affermazione da poco: se l’insieme è abbastanza grande, emergeranno sempre strutture ordinate. Prima ancora che Ramsey sviluppasse tutta la sua teoria, i matematici hanno studiato strutture emergenti non solo in ambito geometrico, ma anche in ambito aritmetico”.
“Per esempio?”.
“Per esempio, nel 1926 un matematico olandese, Bartel van der Waerden, si mise a studiare strutture presenti all’interno di successioni aritmetiche ”.
“Che, ehm, sarebbero?”.
“Le successioni aritmetiche sono successioni di numeri in cui la differenza tra due termini consecutivi è sempre costante. Detto in un altro modo, ogni termine della successione si ottiene dal precedente aggiungendo sempre la stessa costante. Per esempio, la successione 4, 7, 10, 13, 16 è una successione aritmetica”.
“Vero, ogni volta aggiungi 3”.
“Sì: per definire una successione aritmetica serve il punto di partenza, che nel nostro caso è 4, e la costante, che i Veri Matematici chiamano ragione”.
“Che nel nostro caso è 3”.
“Sì. Ora, i problema che studiava van der Waerden è questo: scriviamo tutti i numeri da 1 a 9 in rosso oppure in blu. È sempre vero che possiamo trovare tre numeri rossi o tre numeri blu che formano una progressione aritmetica?”.
“Uhm, con così pochi numeri non mi sembra un problema difficile”.
“Hai ragione, questo è un esempio, giusto per capire come funziona il problema, Puoi risolvere il quesito senza sapere nulla della teoria di Ramsey”.
“Allora ci provo. Vediamo un momento, mi sembra utile partire dal centro della successione. Provo a vedere cosa succede se i numeri 4 e 6 sono colorati di rosso”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Molto bene”.
“Devo sicuramente evitare la progressione 4, 5, 6. E quindi devo colorare 5 di blu”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Pefetto”.
“Però così non ho escluso tutte le possibili progressioni. Per esempio, potrebbe esserci 2, 4, 6. Oppure anche 4, 6, 8. Ok, coloro di blu anche 2 e 8”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Uhm”.
“Cosa succede? Ah! Ho colorato di blu 2, 5, 8, che sono in progressione aritmetica!”.
“E quindi la tua supposizione iniziale non funziona”.
“Hai ragione. Allora 4 e 6 non possono essere colorati entrambi di rosso. E, simmetricamente, nemmeno di blu. Significa che devono avere due colori diversi!”.
“Forse”.
“Giusto, se hanno colori diversi posso sperare di evitare progressioni monocromatiche, ma devo capire se ci riesco. Allora, proviamo. Coloro 4 di rosso e 6 di blu”.
“Senza perdita di generalità”.
“wlog!”.
“Già”.
“Ahh, ho usato wlog anche io, come fanno i Veri Matematici! Allora, parto da qua:”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Bene”.
“Direi di poter colorare il 5 come voglio, anche qui non perdo di generalità se lo coloro di rosso o di blu: in ogni caso non ottengo una progressione aritmetica monocromatica”.
“Giusto”.
“Quindi lo coloro di rosso. Ora la situazione è questa:”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Se 5 fosse blu, la situazione sarebbe simmetrica”.
“Sì, vedo. Con questa configurazione, mi devo preoccupare di non avere il 3 rosso. Se invece 5 fosse blu, mi dovrei preoccupare di non avere il 7 blu. Ho capito. E allora coloro di blu il 3”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“E così hai evitato la progressione rossa di ragione 1. Come prosegui?”.
“Ho già due numeri blu, devo evitare di avere il terzo in progressione. Direi quindi che 9 debba essere rosso”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Bene, così hai evitato di avere 3, 6, 9 monocolore. Hai altre possibilità?”.
“Uhm. Sì, bisogna evitare che 1, 5, 9 sia tutta rossa, quindi 1 va colorato di blu”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Bene, vai avanti”.
“Vedo che 5, 7, 9 rischia di essere tutta rossa, quindi coloro 7 di blu. Però devo evitare che 6, 7, 8 sia blu, quindi coloro 8 di rosso”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Ormai è fatta”.
“Per evitare che 1, 2, 3 sia tutta blu, devo colorare 2 di rosso. Ehi, ma se 2 è rosso dopo ho 2, 5, 8 tutta rossa!”.
“E quindi?”.
“E quindi non ce la faccio a colorare i numeri da 1 a 9 con due colori in modo da non ottenere successioni aritmetiche monocromatiche”.
“Ancora una volta, emerge un ordine”.
“Già. Bell’esercizio, ma van der Waerden non avrà studiato questo problema, vero?”.
“Beh, questo era un esempio semplice. Sai come fanno i Veri Matematici quando risolvono un problema: partendo dal caso semplice, guardano se possono...”.
“...generalizzarlo, ormai ho capito”.
Questa è la terza parte di un articolo uscito sulla rivista Archimede, numero 4, del 2017. La prima parte è qua, la seconda qua.
“Uh, chissà cosa ne pensano i filosofi”.
“Eh, non è un’affermazione da poco: se l’insieme è abbastanza grande, emergeranno sempre strutture ordinate. Prima ancora che Ramsey sviluppasse tutta la sua teoria, i matematici hanno studiato strutture emergenti non solo in ambito geometrico, ma anche in ambito aritmetico”.
“Per esempio?”.
“Per esempio, nel 1926 un matematico olandese, Bartel van der Waerden, si mise a studiare strutture presenti all’interno di successioni aritmetiche ”.
“Che, ehm, sarebbero?”.
“Le successioni aritmetiche sono successioni di numeri in cui la differenza tra due termini consecutivi è sempre costante. Detto in un altro modo, ogni termine della successione si ottiene dal precedente aggiungendo sempre la stessa costante. Per esempio, la successione 4, 7, 10, 13, 16 è una successione aritmetica”.
“Vero, ogni volta aggiungi 3”.
“Sì: per definire una successione aritmetica serve il punto di partenza, che nel nostro caso è 4, e la costante, che i Veri Matematici chiamano ragione”.
“Che nel nostro caso è 3”.
“Sì. Ora, i problema che studiava van der Waerden è questo: scriviamo tutti i numeri da 1 a 9 in rosso oppure in blu. È sempre vero che possiamo trovare tre numeri rossi o tre numeri blu che formano una progressione aritmetica?”.
“Uhm, con così pochi numeri non mi sembra un problema difficile”.
“Hai ragione, questo è un esempio, giusto per capire come funziona il problema, Puoi risolvere il quesito senza sapere nulla della teoria di Ramsey”.
“Allora ci provo. Vediamo un momento, mi sembra utile partire dal centro della successione. Provo a vedere cosa succede se i numeri 4 e 6 sono colorati di rosso”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Molto bene”.
“Devo sicuramente evitare la progressione 4, 5, 6. E quindi devo colorare 5 di blu”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Pefetto”.
“Però così non ho escluso tutte le possibili progressioni. Per esempio, potrebbe esserci 2, 4, 6. Oppure anche 4, 6, 8. Ok, coloro di blu anche 2 e 8”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Uhm”.
“Cosa succede? Ah! Ho colorato di blu 2, 5, 8, che sono in progressione aritmetica!”.
“E quindi la tua supposizione iniziale non funziona”.
“Hai ragione. Allora 4 e 6 non possono essere colorati entrambi di rosso. E, simmetricamente, nemmeno di blu. Significa che devono avere due colori diversi!”.
“Forse”.
“Giusto, se hanno colori diversi posso sperare di evitare progressioni monocromatiche, ma devo capire se ci riesco. Allora, proviamo. Coloro 4 di rosso e 6 di blu”.
“Senza perdita di generalità”.
“wlog!”.
“Già”.
“Ahh, ho usato wlog anche io, come fanno i Veri Matematici! Allora, parto da qua:”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Bene”.
“Direi di poter colorare il 5 come voglio, anche qui non perdo di generalità se lo coloro di rosso o di blu: in ogni caso non ottengo una progressione aritmetica monocromatica”.
“Giusto”.
“Quindi lo coloro di rosso. Ora la situazione è questa:”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Sì, vedo. Con questa configurazione, mi devo preoccupare di non avere il 3 rosso. Se invece 5 fosse blu, mi dovrei preoccupare di non avere il 7 blu. Ho capito. E allora coloro di blu il 3”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Ho già due numeri blu, devo evitare di avere il terzo in progressione. Direi quindi che 9 debba essere rosso”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Uhm. Sì, bisogna evitare che 1, 5, 9 sia tutta rossa, quindi 1 va colorato di blu”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Vedo che 5, 7, 9 rischia di essere tutta rossa, quindi coloro 7 di blu. Però devo evitare che 6, 7, 8 sia blu, quindi coloro 8 di rosso”.
1, 2, 3, 4, 5, 6, 7, 8, 9
“Per evitare che 1, 2, 3 sia tutta blu, devo colorare 2 di rosso. Ehi, ma se 2 è rosso dopo ho 2, 5, 8 tutta rossa!”.
“E quindi?”.
“E quindi non ce la faccio a colorare i numeri da 1 a 9 con due colori in modo da non ottenere successioni aritmetiche monocromatiche”.
“Ancora una volta, emerge un ordine”.
“Già. Bell’esercizio, ma van der Waerden non avrà studiato questo problema, vero?”.
“Beh, questo era un esempio semplice. Sai come fanno i Veri Matematici quando risolvono un problema: partendo dal caso semplice, guardano se possono...”.
“...generalizzarlo, ormai ho capito”.
Questa è la terza parte di un articolo uscito sulla rivista Archimede, numero 4, del 2017. La prima parte è qua, la seconda qua.
giovedì 11 ottobre 2018
Minacce aliene — Parte 2
“Ora, naturalmente ai matematici piace generalizzare”.
“Capirai”.
“Eh, è nella loro natura. Si sono posti quindi questa domanda: se su un grafo formato dai lati e dalle diagonali di un esagono si trova sempre un triangolo monocromatico, che succede con un pentagono? Un quadrilatero? Qual è il numero minimo di vertici che deve avere un grafo completo affinché, colorando i suoi spigoli con due colori, si possa essere certi di formare sempre un triangolo monocromatico?”.
“Beh, certamente non più di 6, no?”.
“Infatti. Se riusciamo a trovare un triangolo che ci piace in un grafo con 6 vertici, aumentando i vertici aumentano anche gli spigoli, e quindi aumentano le possibilità di trovare triangoli monocromatici”.
“Quindi la domanda diventa: potrebbe essere 5, o meno ancora?”.
“Ed ecco la risposta:”.

“Uhm. Un pentagono”.
“Un pentagono con 5 spigoli colorati di rosso e 5 colorati di blu. Osservalo bene: ci sono triangoli monocromatici?”.
“Eh, no”.
“Quindi esiste almeno una colorazione di questo grafo che non produce triangoli monocromatici”.
“E quindi la nostra ricerca è finita: il numero minimo di vertici per avere i triangoli monocromatici è 6. Ottimo, fine della generalizzazione”.
“Non c’è mai fine alle generalizzazioni”.
“Capirai”.
“Per esempio: troverò triangoli anche se uso tre colori? Quattro? Di più?”.
“Ah. Non sembra facile”.
“Non lo è. Ma si può generalizzare anche in un altro modo: posso colorare con 2 colori in modo da trovare triangoli del primo o quadrati del secondo?”.
“Uh, che delirio”.
“E trovare le risposte a queste domande è difficilissimo. Anzi, alcune di queste risposte non le conosciamo ancora”.
“Davvero?”.
“Eh, sì. Il numero che abbiamo calcolato poco fa, il minimo numero di vertici che deve avere un grafo perché si possa sempre trovare al suo interno un triangolo blu o un triangolo rosso, si chiama numero di Ramsey per tre rosso e tre blu, e si indica con R(3,3). Erdős ha detto, una volta: supponete che gli alieni invadano la Terra e che minaccino di annientarla se entro un anno gli uomini non riusciranno a trovare il numero di Ramsey per cinque rosso e cinque blu. Potremmo far scendere in campo le menti migliori e i calcolatori più veloci del pianeta e probabilmente entro un anno riusciremmo a calcolare quel valore. Se tuttavia gli alieni volessero il numero di Ramsey per sei rosso e sei blu. non avremmo altra scelta se non un attacco preventivo.”.
“Eh eh, non credevo fosse così difficile”.
“Lo è, eccome se lo è. I matematici sono riusciti a dimostrare che un numero di Ramsey esiste sempre, qualunque sia il numero di colori e il numero di lati da colorare. Il problema è che non sappiamo quali siano, questi numeri, se non in pochi casi”.
“Ma pensa”.
“Già: per quanto riguarda il famoso R(5,5) di Erdős, nel 1989 si è scoperto che questo numero deve essere almeno 43. Mentre nel 2017, l'anno scorso, si è capito che non può essere più grande di 48”.
“Una scoperta recentissima!”.
“Eh, sì. E, dato che fregiarsi del titolo di potenziale salvatore dagli alieni dovrebbe essere uno stimolo enorme per un Vero Matematico, puoi renderti conto della difficoltà del problema”.
“Quindi di pensare a risolvere R(6,6) non se ne parla proprio, suppongo. Meglio sviluppare la tecnologia per combattere gli alieni?”.
“Le ultime stime per R(6,6) sono del 1965. Da allora, nessuno è riuscito a fare meglio. Sappiamo solo che R(6,6) è un numero compreso tra 102 e 165”.
“Eppure non sono numeri così grandi, come è possibile che non si riescano a migliorare le stime?”.
“Ricordati che i numeri di cui stiamo parlando sono i vertici. Sai quanti spigoli ha un grafo completo con 100 vertici?”.
“Eh, al momento no...”.
“Prova a pensare: quanti spigoli partono da ogni vertice?”.
“Eh, direi 99, uno per ogni vertice, tranne quello da cui parto”.
“E dato che ci sono 100 vertici...”.
“Ho 100×99 spigoli?”.
“Non esattamente. In questo modo, ogni spigolo verrebbe contato due volte, una per il vertice di partenza e una per quello di arrivo”.
“Ah, allora devo dividere per due il risultato!”.
“Già. Quindi un grafo con 100 vertici ha 50×99 spigoli, cioè 4950”.
“Anche questo non è un numero così esagerato, magari con un computer si può fare qualche stima, no?”.
“Eh, sai quante possibili colorazioni si possono fare, anche soltanto con due colori?”.
“Uhm, non saprei come calcolarle”.
“Non è difficile: per ogni spigolo hai due scelte, o lo colori di blu o di rosso. Quindi due scelte per il primo spigolo, moltiplicate per altre due scelte per il secondo, e così via”.
“Gulp, devo moltiplicare 2 per sé stesso 4950 volte”.
“Esatto. Un numero composto da 1491 cifre. Se passi a un grafo con 120 vertici ti risulta un numero di configurazioni da provare composto da 2150 cifre”.
“Comincia a diventare lunghetta”.
“E non è finita: in ognuna delle configurazioni devi cercare degli esagoni”.
“Argh”.
“In un grafo completo sei vertici scelti a caso sono sempre collegati da sei spigoli, quindi per calcolare il numero di esagoni ti basta calcolare il numero di possibili scelte di sei vertici”.
“E come faccio?”.
“Beh, il primo vertice lo puoi scegliere in 100 modi diversi, il secondo in 99, il terzo in 98, e così via, fino al sesto vertice, che puoi scegliere in 95 modi. In realtà queste scelte non sono tutte diverse, puoi mescolare i sei lati in 6! modi, come se fossero le lettere di un anagramma”.
“Totale: 100×99×98×97×96×95. Poi divido per il fattoriale di 6, vediamo… fa 1 miliardo e rotti. E dovrei controllarli tutti per ognuno dei grafi? Roba da matti”.
“Come vedi, non esiste ancora la potenza di calcolo necessaria per poter affrontare questo problema con la forza bruta. Meglio attaccare gli alieni”.
“Ma allora come hanno fatto a fare quelle stime di cui parlavi? ”.
“Erdős è stato il primo a farle, e ha escogitato un metodo che, a prima vista, è spiazzante. I Veri Matematici lo chiamano metodo probabilistico”.
“Uhm, usa la probabilità? Si può dimostrare un teorema con considerazioni di probabilità? Mi pareva che i teoremi dessero certezze”.
“Eh, è proprio per questo che il metodo è spiazzante: Erdős ha usato la probabilità per arrivare a una vera dimostrazione”.
“Uh”.
“Erdős partiva da questa idea: supponiamo di colorare gli spigoli di un grafo in maniera casuale, tirando una moneta. Se viene testa coloro lo spigolo di rosso, se viene croce lo coloro di blu”.
“Va bene”.
“Ora, supponiamo di voler fare una stima dal basso di R(34,34)”.
“Un numero impossibile da calcolare, se già R(6,6) è intrattabile”.
“Esattamente: questo esempio serve per capire la potenza del metodo probabilistico. Ci chiediamo, ad esempio, se un grafo con un milione di vertici potrebbe essere sufficiente per garantire la presenza di poligoni di 34 lati monocromatici”.
“Mi immagino il disegno”.
“Eh eh. Ora, un grafo completo con 34 vertici ha 561 spigoli”.
“Vediamo se ho capito: per ogni spigolo posso scegliere il primo vertice in 34 modi, e il secondo in 33, però così facendo conto gli spigoli due volte, quindi dopo aver moltiplicato 34 per 33 devo dividere per 2. Sì, risulta 561”.
“Esattamente. Ora la probabilità che questi 561 vertici siano tutti dello stesso colore”.
“Ho probabilità un mezzo per ogni lato, quindi dovrebbe essere (1/2)561”.
“Bene, però i colori sono due”.
“Quindi moltiplico per due, e mi viene (1/2)560”.
“Ok. Quanti poligoni di 34 lati abbiamo in un grafo di un milione di vertici?”.
“Oh, tanti. Avevamo visto che già il calcolo con 100 dava un numero molto grande”.
“Eh, sì. Procedendo allo stesso modo, risulta che il numero di combinazioni è circa 3×10165. A questo punto, possiamo chiederci quanto vale la probabilità di trovare un poligono di 34 lati monocromatico”.
“Devo moltiplicare la probabilità che un singolo poligono sia monocromatico con il numero dei poligoni, no?”.
“Vero”.
“Quindi devo moltiplicare (1/2)560 per 3×10165”.
“Quanto viene?”.
“Poco meno di un millesimo”.
“Non importa il valore esatto, ciò che conta è che il risultato sia minore di 1”.
“Perché?”.
“Perché se tutte le possibili colorazioni di spigoli contenessero poligoni di 34 lati monocromatici, allora questa probabilità dovrebbe essere uguale a 1”.
“Ah, vero: avremmo la certezza di trovare un poligono monocromatico”.
“Dunque, se la probabilità è minore di uno, ciò significa che esiste almeno una colorazione che non ci dà poligoni monocromatici”.
“E quindi?”.
“E quindi un milione di vertici sono troppo pochi: abbiamo trovato una limitazione inferiore per R(34,34)”.
“Ah. Non è stato così difficile”.
“Per questo il metodo è potente: permette di capire qualcosa in un universo di calcoli proibitivi”.
“Ordine nel caos”.
“Proprio così. Come disse il matematico Theodore Motzkin descrivendo la teoria di Ramsey: complete disorder is impossible”.
Questa è la seconda parte di un articolo uscito sulla rivista Archimede, numero 4, del 2017. La prima parte è qua.
“Capirai”.
“Eh, è nella loro natura. Si sono posti quindi questa domanda: se su un grafo formato dai lati e dalle diagonali di un esagono si trova sempre un triangolo monocromatico, che succede con un pentagono? Un quadrilatero? Qual è il numero minimo di vertici che deve avere un grafo completo affinché, colorando i suoi spigoli con due colori, si possa essere certi di formare sempre un triangolo monocromatico?”.
“Beh, certamente non più di 6, no?”.
“Infatti. Se riusciamo a trovare un triangolo che ci piace in un grafo con 6 vertici, aumentando i vertici aumentano anche gli spigoli, e quindi aumentano le possibilità di trovare triangoli monocromatici”.
“Quindi la domanda diventa: potrebbe essere 5, o meno ancora?”.
“Ed ecco la risposta:”.
“Uhm. Un pentagono”.
“Un pentagono con 5 spigoli colorati di rosso e 5 colorati di blu. Osservalo bene: ci sono triangoli monocromatici?”.
“Eh, no”.
“Quindi esiste almeno una colorazione di questo grafo che non produce triangoli monocromatici”.
“E quindi la nostra ricerca è finita: il numero minimo di vertici per avere i triangoli monocromatici è 6. Ottimo, fine della generalizzazione”.
“Non c’è mai fine alle generalizzazioni”.
“Capirai”.
“Per esempio: troverò triangoli anche se uso tre colori? Quattro? Di più?”.
“Ah. Non sembra facile”.
“Non lo è. Ma si può generalizzare anche in un altro modo: posso colorare con 2 colori in modo da trovare triangoli del primo o quadrati del secondo?”.
“Uh, che delirio”.
“E trovare le risposte a queste domande è difficilissimo. Anzi, alcune di queste risposte non le conosciamo ancora”.
“Davvero?”.
“Eh, sì. Il numero che abbiamo calcolato poco fa, il minimo numero di vertici che deve avere un grafo perché si possa sempre trovare al suo interno un triangolo blu o un triangolo rosso, si chiama numero di Ramsey per tre rosso e tre blu, e si indica con R(3,3). Erdős ha detto, una volta: supponete che gli alieni invadano la Terra e che minaccino di annientarla se entro un anno gli uomini non riusciranno a trovare il numero di Ramsey per cinque rosso e cinque blu. Potremmo far scendere in campo le menti migliori e i calcolatori più veloci del pianeta e probabilmente entro un anno riusciremmo a calcolare quel valore. Se tuttavia gli alieni volessero il numero di Ramsey per sei rosso e sei blu. non avremmo altra scelta se non un attacco preventivo.”.
“Eh eh, non credevo fosse così difficile”.
“Lo è, eccome se lo è. I matematici sono riusciti a dimostrare che un numero di Ramsey esiste sempre, qualunque sia il numero di colori e il numero di lati da colorare. Il problema è che non sappiamo quali siano, questi numeri, se non in pochi casi”.
“Ma pensa”.
“Già: per quanto riguarda il famoso R(5,5) di Erdős, nel 1989 si è scoperto che questo numero deve essere almeno 43. Mentre nel 2017, l'anno scorso, si è capito che non può essere più grande di 48”.
“Una scoperta recentissima!”.
“Eh, sì. E, dato che fregiarsi del titolo di potenziale salvatore dagli alieni dovrebbe essere uno stimolo enorme per un Vero Matematico, puoi renderti conto della difficoltà del problema”.
“Quindi di pensare a risolvere R(6,6) non se ne parla proprio, suppongo. Meglio sviluppare la tecnologia per combattere gli alieni?”.
“Le ultime stime per R(6,6) sono del 1965. Da allora, nessuno è riuscito a fare meglio. Sappiamo solo che R(6,6) è un numero compreso tra 102 e 165”.
“Eppure non sono numeri così grandi, come è possibile che non si riescano a migliorare le stime?”.
“Ricordati che i numeri di cui stiamo parlando sono i vertici. Sai quanti spigoli ha un grafo completo con 100 vertici?”.
“Eh, al momento no...”.
“Prova a pensare: quanti spigoli partono da ogni vertice?”.
“Eh, direi 99, uno per ogni vertice, tranne quello da cui parto”.
“E dato che ci sono 100 vertici...”.
“Ho 100×99 spigoli?”.
“Non esattamente. In questo modo, ogni spigolo verrebbe contato due volte, una per il vertice di partenza e una per quello di arrivo”.
“Ah, allora devo dividere per due il risultato!”.
“Già. Quindi un grafo con 100 vertici ha 50×99 spigoli, cioè 4950”.
“Anche questo non è un numero così esagerato, magari con un computer si può fare qualche stima, no?”.
“Eh, sai quante possibili colorazioni si possono fare, anche soltanto con due colori?”.
“Uhm, non saprei come calcolarle”.
“Non è difficile: per ogni spigolo hai due scelte, o lo colori di blu o di rosso. Quindi due scelte per il primo spigolo, moltiplicate per altre due scelte per il secondo, e così via”.
“Gulp, devo moltiplicare 2 per sé stesso 4950 volte”.
“Esatto. Un numero composto da 1491 cifre. Se passi a un grafo con 120 vertici ti risulta un numero di configurazioni da provare composto da 2150 cifre”.
“Comincia a diventare lunghetta”.
“E non è finita: in ognuna delle configurazioni devi cercare degli esagoni”.
“Argh”.
“In un grafo completo sei vertici scelti a caso sono sempre collegati da sei spigoli, quindi per calcolare il numero di esagoni ti basta calcolare il numero di possibili scelte di sei vertici”.
“E come faccio?”.
“Beh, il primo vertice lo puoi scegliere in 100 modi diversi, il secondo in 99, il terzo in 98, e così via, fino al sesto vertice, che puoi scegliere in 95 modi. In realtà queste scelte non sono tutte diverse, puoi mescolare i sei lati in 6! modi, come se fossero le lettere di un anagramma”.
“Totale: 100×99×98×97×96×95. Poi divido per il fattoriale di 6, vediamo… fa 1 miliardo e rotti. E dovrei controllarli tutti per ognuno dei grafi? Roba da matti”.
“Come vedi, non esiste ancora la potenza di calcolo necessaria per poter affrontare questo problema con la forza bruta. Meglio attaccare gli alieni”.
“Ma allora come hanno fatto a fare quelle stime di cui parlavi? ”.
“Erdős è stato il primo a farle, e ha escogitato un metodo che, a prima vista, è spiazzante. I Veri Matematici lo chiamano metodo probabilistico”.
“Uhm, usa la probabilità? Si può dimostrare un teorema con considerazioni di probabilità? Mi pareva che i teoremi dessero certezze”.
“Eh, è proprio per questo che il metodo è spiazzante: Erdős ha usato la probabilità per arrivare a una vera dimostrazione”.
“Uh”.
“Erdős partiva da questa idea: supponiamo di colorare gli spigoli di un grafo in maniera casuale, tirando una moneta. Se viene testa coloro lo spigolo di rosso, se viene croce lo coloro di blu”.
“Va bene”.
“Ora, supponiamo di voler fare una stima dal basso di R(34,34)”.
“Un numero impossibile da calcolare, se già R(6,6) è intrattabile”.
“Esattamente: questo esempio serve per capire la potenza del metodo probabilistico. Ci chiediamo, ad esempio, se un grafo con un milione di vertici potrebbe essere sufficiente per garantire la presenza di poligoni di 34 lati monocromatici”.
“Mi immagino il disegno”.
“Eh eh. Ora, un grafo completo con 34 vertici ha 561 spigoli”.
“Vediamo se ho capito: per ogni spigolo posso scegliere il primo vertice in 34 modi, e il secondo in 33, però così facendo conto gli spigoli due volte, quindi dopo aver moltiplicato 34 per 33 devo dividere per 2. Sì, risulta 561”.
“Esattamente. Ora la probabilità che questi 561 vertici siano tutti dello stesso colore”.
“Ho probabilità un mezzo per ogni lato, quindi dovrebbe essere (1/2)561”.
“Bene, però i colori sono due”.
“Quindi moltiplico per due, e mi viene (1/2)560”.
“Ok. Quanti poligoni di 34 lati abbiamo in un grafo di un milione di vertici?”.
“Oh, tanti. Avevamo visto che già il calcolo con 100 dava un numero molto grande”.
“Eh, sì. Procedendo allo stesso modo, risulta che il numero di combinazioni è circa 3×10165. A questo punto, possiamo chiederci quanto vale la probabilità di trovare un poligono di 34 lati monocromatico”.
“Devo moltiplicare la probabilità che un singolo poligono sia monocromatico con il numero dei poligoni, no?”.
“Vero”.
“Quindi devo moltiplicare (1/2)560 per 3×10165”.
“Quanto viene?”.
“Poco meno di un millesimo”.
“Non importa il valore esatto, ciò che conta è che il risultato sia minore di 1”.
“Perché?”.
“Perché se tutte le possibili colorazioni di spigoli contenessero poligoni di 34 lati monocromatici, allora questa probabilità dovrebbe essere uguale a 1”.
“Ah, vero: avremmo la certezza di trovare un poligono monocromatico”.
“Dunque, se la probabilità è minore di uno, ciò significa che esiste almeno una colorazione che non ci dà poligoni monocromatici”.
“E quindi?”.
“E quindi un milione di vertici sono troppo pochi: abbiamo trovato una limitazione inferiore per R(34,34)”.
“Ah. Non è stato così difficile”.
“Per questo il metodo è potente: permette di capire qualcosa in un universo di calcoli proibitivi”.
“Ordine nel caos”.
“Proprio così. Come disse il matematico Theodore Motzkin descrivendo la teoria di Ramsey: complete disorder is impossible”.
Questa è la seconda parte di un articolo uscito sulla rivista Archimede, numero 4, del 2017. La prima parte è qua.
venerdì 7 settembre 2018
Minacce aliene — Parte 1
Gli alieni invadono la Terra e minacciano di annientarla se entro un anno gli uomini non riusciranno a trovare il numero di Ramsey per cinque rosso e cinque blu. Potremmo far scendere in campo le menti migliori e i calcolatori più veloci del pianeta e probabilmente entro un anno riusciremmo a calcolare quel valore. Se tuttavia gli alieni volessero il numero di Ramsey per sei rosso e sei blu, non avremmo altra scelta se non un attacco preventivo.
“Com’è questa faccenda degli alieni?”.
“Te lo spiego con un gioco”.
“Oh, bene!”.
“Abbiamo questo schema. A turno dobbiamo colorare i segmenti che collegano i punti: io uso il rosso, tu usi il blu. Naturalmente se uno di noi ha colorato un segmento, l’altro non può colorarlo di nuovo”.
“Ok”.
“Perde il primo che forma un triangolo. Comincia tu ”.
“Uhm”.
“Cosa c’è?”.
“Di solito, quando un Vero Matematico propone un gioco, è sicuro di vincere”.
“Eh, c’è del vero in quello che dici”.
“E quindi, se le cose stanno così, io non ho nemmeno la speranza di riuscire a pareggiare. Figuriamoci se posso pensare di vincere”.
“In effetti in questo gioco non è possibile pareggiare, nemmeno giocando male”.
“Davvero? E come è possibile? Non dirmi che, anche colorando i lati a caso, si riesce sempre a creare un triangolo”.
“E invece è proprio così. In questo gioco è impossibile non avere un triangolo. Prova: colora a caso alternativamente di rosso e di blu i segmenti, e guarda come va a finire”.
“Uh, è vero. Però, se non sbaglio, un caso favorevole non dimostra un’affermazione, no?”.
“Molto bene, vedo che i miei sforzi hanno prodotto qualche risultato”.
“Eh, so che i Veri Matematici tengono molto alle loro dimostrazioni, e so che questa non lo è. E mi è venuta anche la curiosità di sapere come si possa affermare che è sempre possibile trovare un triangolo colorato”.
“Bene, bene. La dimostrazione non è difficile: il campo di gara di questo gioco...”.
“A proposito: ha un nome?”.
“Sì, si chiama Sim. Dicevo, il campo di gara è quello che i Veri Matematici chiamano grafo completo composto da 6 vertici”.
“Un esagono con tutte le sue diagonali”.
“Esatto. Qui trattiamo le diagonali vere e proprie e i lati dell’esagono allo stesso modo: li chiamiamo spigoli. Da ogni vertice escono naturalmente cinque spigoli”.
“Naturalmente”.
“Quindi almeno tre verranno colorati allo stesso modo”.
“Uhm, perché?”.
“Vuoi assegnare ogni diagonale a un colore: è come se tu dovessi distribuire cinque maglie in due cassetti, quello rosso e quello blu”.
“Cosa c’entrano le maglie?”.
“E’ un esempio: distribuisci cinque maglie in due cassetti. Quante maglie andranno in ogni cassetto?”.
“Boh, dipende”.
“Mettere una maglia in un cassetto corrisponde a colorare uno dei cinque spigoli. Riesci a fare in modo che nessuno dei due cassetti contenga tre maglie?”.
“Eh, no, è impossibile: posso mettere due maglie in ogni cassetto, per un totale di quattro maglie. Poi però mi rimane la quinta, e da qualche parte devo mettere pure quella”.
“Quindi uno dei due cassetti avrà almeno tre maglie”.
“Perché almeno?”.
“Perché potresti anche mettere tutte le maglie nello stesso cassetto. Qualunque cosa tu faccia, un cassetto conterrà certamente più di due maglie”.
“Va bene”.
“E quindi, comunque tu scelga una colorazione dei cinque spigoli che partono da un vertice dell’esagono, almeno tre di essi avranno lo stesso colore”.
“D’accordo”.
“Supponiamo che sia il blu”.
“Immagino che la dimostrazione con tre spigoli rossi sia simmetrica a questa”.
“Esattamente. I Veri Matematici usano così spesso queste simmetrie che hanno coniato un acronimo apposta: invece di scrivere che la scelta che hanno fatto non fa perdere di generalità al problema, scrivono wlog”.
“Una funzione? Una specie di logaritmo? Che roba è?”.
“Un acronimo: without loss of generality. Alcuni lo usano anche quando parlano”.
“Sono pazzi”.
“Eh, un po’. Ma andiamo avanti: chiamiamo V il vertice che abbiamo scelto. V è connesso con altri tre vertici, che possiamo chiamare R, S e T. Se uno qualsiasi degli spigoli RS, ST o RT è blu, allora abbiamo trovato un triangolo blu. Se nessuno dei tre invece è blu...”.
“...allora abbiamo un triangolo rosso!”.
“Quello di vertici R, S e T, esatto.”.
“E quindi è vero che in una qualsiasi colorazione degli spigoli di questo grafo troviamo sempre un triangolo con i lati dello stesso colore”.
“Una qualsiasi colorazione fatta con due soli colori, naturalmente”.
“Ah, sì, certo. Dunque, al gioco del Sim non si può pareggiare”.
“Proprio così. Ora, naturalmente ai matematici piace generalizzare”.
“Capirai”.
Questa è la prima parte di un articolo uscito sulla rivista Archimede, numero 4, del 2017.
domenica 19 agosto 2018
Come di consueto, classifiche (questa volta non olimpiche)
Ecco la classifica definitiva dei campionati europei 2018, ordinata come al solito secondo la proposta di Simon Tatham.
Uno stato X è stato migliore di un altro stato Y se il medagliere di Y può essere trasformato nel medagliere di X mediante una sequenza di aggiunte di medaglie oppure di sostituzione di medaglie basse con medaglie alte.
Uno stato X è stato migliore di un altro stato Y se il medagliere di Y può essere trasformato nel medagliere di X mediante una sequenza di aggiunte di medaglie oppure di sostituzione di medaglie basse con medaglie alte.
sabato 2 giugno 2018
L'inverso del teorema di Pitagora
“L'inverso del teorema di Pitagora?”.
“Eh, sì”.
“Ma cosa significa inverso?”.
“Ti giro la domanda: cosa dice il teorema di Pitagora?”.
“Dice che il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti”.
“No”.
“Come no?”.
“No: prendi un triangolo equilatero di lato 1 e dimmi se è vero che 1 + 1 = 1”.
“Ma cosa c'entra un triangolo equilatero? Il triangolo deve essere… Ok, non l'ho detto”.
“Già”.
“Riprovo: il teorema di Pitagora dice che in un triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti”.
“Ottimo. Qual era l'errore, quindi?”.
“Avevo dimenticato di specificare il contesto in cui si applica il teorema”.
“Sì, avevi dimenticato l'ipotesi: il teorema di Pitagora vale se il triangolo è rettangolo”.
“E l'inverso, allora?”.
“L'inverso risponde a quest'altra domanda: è vero o no che il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti solo se il triangolo è rettangolo?”.
“Ovvio”.
“Mica tanto ovvio: prendi un triangolo, indica con a, b e c i suoi tre lati, sai che vale la relazione a2 + b2 = c2. Puoi dire che il triangolo è rettangolo?”.
“Ma per forza, no?”.
“NO! NON ESISTONO DIMOSTRAZIONI PER FORZA!”.
“Ok, ok, mamma mia che brutto carattere”.
“Scusa eh, ma se tu sai che il verificarsi di qualcosa implica il verificarsi di qualcos'altro, puoi dire che automaticamente il verificarsi della seconda cosa implica il verificarsi della prima?”.
“Fino a pochi secondi fa avrei detto di sì, ma mi pare di capire che invece non sia così. Ho un po' paura a chiedere perché, però”.
“Prendi un numero divisibile per 4: puoi dire che è divisibile anche per 2?”.
“Certo”.
“Perché?”.
“Perché se contiene 4 contiene anche 2, dato che 4 è divisibile per 2”.
“Questa proprietà vale per tutti i numeri divisibili per 4?”.
“Certo”.
“Puoi dire il contrario? Puoi dire che ogni numero divisibile per 2 è divisibile anche per 4?”.
“Eh, no, non tutti. Se prendo 8 va bene, se prendo 6 no”.
“Quindi questo è un esempio di teorema che funziona in una sola direzione: il suo inverso non è un teorema”.
“Ah”.
“È vero che un quadrato ha quattro angoli retti?”.
“Certo”.
“È vero il contrario? Che se un quadrilatero ha quattro angoli retti allora è un quadrato?”.
“Eh, no, un rettangolo ha quattro angoli retti ma non è un quadrato”.
“Non è detto che lo sia, volendo essere precisi”.
“Può esserlo?”.
“Beh, sì. Se la definizione di rettangolo è quadrilatero con quattro angoli retti, allora esso potrebbe anche essere un quadrato. Ma non è vero che ogni rettangolo è un quadrato”.
“Va bene, ho capito”.
“Tornando al teorema di Pitagora: è vero che se in un triangolo il quadrato di un lato è equivalente alla somma dei quadrati degli altri due lati, allora quel triangolo è rettangolo”.
“A questo punto non so più quale sia la risposta. Direi di sì, ma non so perché”.
“La risposta è sì, anche se ormai il motivo per cui quella risposta è affermativa è sparito dai libri scolastici”.
“Perché?”.
“Non ne ho idea. Pigrizia? Poca voglia di spiegare? Chissà”.
“Ma è una dimostrazione difficile?”.
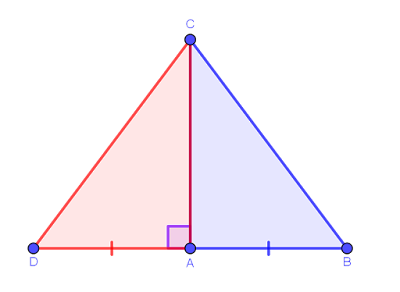
“No, non direi. Te la mostro, nella versione di Euclide. Cominciamo da un triangolo ABC per il quale vale la relazione AB2 + AC2 = BC2. Eccolo qua”.
“Ok. Quindi non sappiamo se è rettangolo, e vogliamo dimostrarlo”.
“Esatto: vogliamo dimostrare che l'angolo in A è retto”.
“Va bene, cominciamo”.
“Dobbiamo fare una costruzione: costruiamo un segmento DA che forma un angolo retto con CA”.
“Quindi prolunghiamo AB? Ma non sappiamo se l'angolo A è retto oppure no”.
“Esatto, ottimo: non prolunghiamo, ma costruiamo noi un angolo che sia retto. Questo vuol dire che ancora non possiamo sapere se i tre punti D, A e B sono allineati oppure no”.
“Ho capito. Quanto deve essere lungo il segmento DA?”.
“Tanto quanto AB”.
“Perfetto, eccolo qua”.
“Poi congiungiamo D con C e formiamo un triangolo”.
“E, questa volta, sappiamo che è un triangolo rettangolo”.
“Proprio così, ecco la figura completa”.
“Ora che si fa?”.
“Scriviamo un po' di uguaglianze. La prima è questa, sei d'accordo? DA2 = AB2”.
“Eh, beh, sì, se DA è uguale a AB lo saranno anche i loro quadrati”.
“Già. Ora aggiungiamo, a destra e a sinistra dell'uguale, la stessa quantità, cioè AC2”.
“Così? DA2 + AC2 = AB2 + AC2”.
“Esatto. Ora guarda cosa c'è a sinistra dell'uguale”.
“C'è la somma dei quadrati di DA e AC… Ah! Il triangolo DAC è rettangolo, quindi per quello posso applicare il teorema di Pitagora, vero?”.
“Certo: questa dimostrazione si appoggia su quel teorema. Prima dimostri il teorema diretto, poi questo”.
“Ah. Ma si può?”.
“Certo, non stai facendo le cose in modo circolare: prima dimostri il teorema di Pitagora, senza usare questo teorema, poi dimostri questo usando quello che hai appena dimostrato”.
“Ok, mi piace. Quindi siamo arrivati al fatto che a sinistra dell'uguale si può applicare il teorema di Pitagora: lo facciamo?”.
“Sì, e quindi possiamo sostituire, al posto di DA2 + AC2, il quadrato dell'ipotenusa, cioè DC2”.
“A destra dell'uguale, però, non posso farlo, perché non so se il triangolo sia rettangolo oppure no”.
“No, ma non ti serve saperlo: per la parte di destra puoi usare direttamente l'ipotesi. Tu sai già quanto vale quella somma”.
“Ehi, ma è vero, è proprio l'ipotesi! So che AB2 + AC2 è uguale a BC2”.
“Certo, e quindi l'uguaglianza è diventata DC2 = BC2”.
“Ma allora posso dire che DC e BC sono uguali”.
“Proprio così: quindi i due triangoli ABC e ACD hanno i tre lati ordinatamente congruenti”.
“E allora sono triangoli congruenti, no?”.
“Sì, è così, per il cosiddetto terzo criterio di congruenza dei triangoli. A questo punto, abbiamo concluso: se i due angoli DAC e CAB sono congruenti…”.
“…dato che DAC è retto, dovrà esserlo anche CAB!”.
“Ed ecco fatto”.
“Avevi ragione, non era difficile. Dicevi che sui libri di scuola non si trova più questa dimostrazione, ma perché? Non è difficile, mi sembra un peccato non metterla”.
“Anche a me”.
“Eh, sì”.
“Ma cosa significa inverso?”.
“Ti giro la domanda: cosa dice il teorema di Pitagora?”.
“Dice che il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti”.
“No”.
“Come no?”.
“No: prendi un triangolo equilatero di lato 1 e dimmi se è vero che 1 + 1 = 1”.
“Ma cosa c'entra un triangolo equilatero? Il triangolo deve essere… Ok, non l'ho detto”.
“Già”.
“Riprovo: il teorema di Pitagora dice che in un triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti”.
“Ottimo. Qual era l'errore, quindi?”.
“Avevo dimenticato di specificare il contesto in cui si applica il teorema”.
“Sì, avevi dimenticato l'ipotesi: il teorema di Pitagora vale se il triangolo è rettangolo”.
“E l'inverso, allora?”.
“L'inverso risponde a quest'altra domanda: è vero o no che il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti solo se il triangolo è rettangolo?”.
“Ovvio”.
“Mica tanto ovvio: prendi un triangolo, indica con a, b e c i suoi tre lati, sai che vale la relazione a2 + b2 = c2. Puoi dire che il triangolo è rettangolo?”.
“Ma per forza, no?”.
“NO! NON ESISTONO DIMOSTRAZIONI PER FORZA!”.
“Ok, ok, mamma mia che brutto carattere”.
“Scusa eh, ma se tu sai che il verificarsi di qualcosa implica il verificarsi di qualcos'altro, puoi dire che automaticamente il verificarsi della seconda cosa implica il verificarsi della prima?”.
“Fino a pochi secondi fa avrei detto di sì, ma mi pare di capire che invece non sia così. Ho un po' paura a chiedere perché, però”.
“Prendi un numero divisibile per 4: puoi dire che è divisibile anche per 2?”.
“Certo”.
“Perché?”.
“Perché se contiene 4 contiene anche 2, dato che 4 è divisibile per 2”.
“Questa proprietà vale per tutti i numeri divisibili per 4?”.
“Certo”.
“Puoi dire il contrario? Puoi dire che ogni numero divisibile per 2 è divisibile anche per 4?”.
“Eh, no, non tutti. Se prendo 8 va bene, se prendo 6 no”.
“Quindi questo è un esempio di teorema che funziona in una sola direzione: il suo inverso non è un teorema”.
“Ah”.
“È vero che un quadrato ha quattro angoli retti?”.
“Certo”.
“È vero il contrario? Che se un quadrilatero ha quattro angoli retti allora è un quadrato?”.
“Eh, no, un rettangolo ha quattro angoli retti ma non è un quadrato”.
“Non è detto che lo sia, volendo essere precisi”.
“Può esserlo?”.
“Beh, sì. Se la definizione di rettangolo è quadrilatero con quattro angoli retti, allora esso potrebbe anche essere un quadrato. Ma non è vero che ogni rettangolo è un quadrato”.
“Va bene, ho capito”.
“Tornando al teorema di Pitagora: è vero che se in un triangolo il quadrato di un lato è equivalente alla somma dei quadrati degli altri due lati, allora quel triangolo è rettangolo”.
“A questo punto non so più quale sia la risposta. Direi di sì, ma non so perché”.
“La risposta è sì, anche se ormai il motivo per cui quella risposta è affermativa è sparito dai libri scolastici”.
“Perché?”.
“Non ne ho idea. Pigrizia? Poca voglia di spiegare? Chissà”.
“Ma è una dimostrazione difficile?”.
“No, non direi. Te la mostro, nella versione di Euclide. Cominciamo da un triangolo ABC per il quale vale la relazione AB2 + AC2 = BC2. Eccolo qua”.
“Ok. Quindi non sappiamo se è rettangolo, e vogliamo dimostrarlo”.
“Esatto: vogliamo dimostrare che l'angolo in A è retto”.
“Va bene, cominciamo”.
“Dobbiamo fare una costruzione: costruiamo un segmento DA che forma un angolo retto con CA”.
“Quindi prolunghiamo AB? Ma non sappiamo se l'angolo A è retto oppure no”.
“Esatto, ottimo: non prolunghiamo, ma costruiamo noi un angolo che sia retto. Questo vuol dire che ancora non possiamo sapere se i tre punti D, A e B sono allineati oppure no”.
“Ho capito. Quanto deve essere lungo il segmento DA?”.
“Tanto quanto AB”.
“Perfetto, eccolo qua”.
“Poi congiungiamo D con C e formiamo un triangolo”.
“E, questa volta, sappiamo che è un triangolo rettangolo”.
“Proprio così, ecco la figura completa”.
“Ora che si fa?”.
“Scriviamo un po' di uguaglianze. La prima è questa, sei d'accordo? DA2 = AB2”.
“Eh, beh, sì, se DA è uguale a AB lo saranno anche i loro quadrati”.
“Già. Ora aggiungiamo, a destra e a sinistra dell'uguale, la stessa quantità, cioè AC2”.
“Così? DA2 + AC2 = AB2 + AC2”.
“Esatto. Ora guarda cosa c'è a sinistra dell'uguale”.
“C'è la somma dei quadrati di DA e AC… Ah! Il triangolo DAC è rettangolo, quindi per quello posso applicare il teorema di Pitagora, vero?”.
“Certo: questa dimostrazione si appoggia su quel teorema. Prima dimostri il teorema diretto, poi questo”.
“Ah. Ma si può?”.
“Certo, non stai facendo le cose in modo circolare: prima dimostri il teorema di Pitagora, senza usare questo teorema, poi dimostri questo usando quello che hai appena dimostrato”.
“Ok, mi piace. Quindi siamo arrivati al fatto che a sinistra dell'uguale si può applicare il teorema di Pitagora: lo facciamo?”.
“Sì, e quindi possiamo sostituire, al posto di DA2 + AC2, il quadrato dell'ipotenusa, cioè DC2”.
“A destra dell'uguale, però, non posso farlo, perché non so se il triangolo sia rettangolo oppure no”.
“No, ma non ti serve saperlo: per la parte di destra puoi usare direttamente l'ipotesi. Tu sai già quanto vale quella somma”.
“Ehi, ma è vero, è proprio l'ipotesi! So che AB2 + AC2 è uguale a BC2”.
“Certo, e quindi l'uguaglianza è diventata DC2 = BC2”.
“Ma allora posso dire che DC e BC sono uguali”.
“Proprio così: quindi i due triangoli ABC e ACD hanno i tre lati ordinatamente congruenti”.
“E allora sono triangoli congruenti, no?”.
“Sì, è così, per il cosiddetto terzo criterio di congruenza dei triangoli. A questo punto, abbiamo concluso: se i due angoli DAC e CAB sono congruenti…”.
“…dato che DAC è retto, dovrà esserlo anche CAB!”.
“Ed ecco fatto”.
“Avevi ragione, non era difficile. Dicevi che sui libri di scuola non si trova più questa dimostrazione, ma perché? Non è difficile, mi sembra un peccato non metterla”.
“Anche a me”.
giovedì 10 maggio 2018
Come fanno i computer a calcolare le radici quadrate? — Parte 2: l'algoritmo Karatsuba
“La volta scorsa abbiamo visto come si calcola a mano una radice quadrata”.
“Ricordo. Una radice quadrata con resto, se ben ricordo”.
“Esatto. Per essere precisi: dato un numero m, diciamo che s è la sua radice quadrata e r è il resto se valgono queste relazioni:”.
s2 ≤ m = s2 + r < (s + 1)2
“E abbiamo detto che i computer seguono un algoritmo simile”.
“Ancora esatto: adattano questo algoritmo alle loro caratteristiche, sfruttano la base 2 invece della base 10, e sfruttano soprattutto il fatto di essere molto bravi a compiere operazioni ripetitive. In sostanza imparano a fare i calcoli con un caso relativamente facile, e se poi i numeri diventano troppo grossi allora li spezzettano in modo da ridurre il caso difficile a tanti casi facili”.
“Bello”.
“Posso farti vedere un programmino che simula quello che viene fatto effettivamente dall'algoritmo”.
“Perché dici simula?”.
“Perché le vere implementazioni sono al solito complicate da casi particolari relativi a quanto sono lunghi i gruppi di bit che ogni macchina riesce a gestire velocemente, e quindi i veri sorgenti sono pieni di controlli del tipo se lavori con 32 bit allora fai questo, se invece lavori con 64 allora fai quest'altro, e cose così”.
“Roba da informatici”.
“Già. E poi, per semplicità, il mio programmino funziona in base 10”.
“Ok”.
“L'algoritmo si chiama SqrtRem”.
“Bel nome, molto evocativo”.
“Non l'ho scelto io: è il nome che gli autori della libreria GMP hanno scelto; la prima parte, Sqrt, significa Square Root, cioè radice quadrata, e la seconda, Rem, sta per remainder, cioè resto”.
“Va bene, non critico più i nomi scelti dagli informatici”.
“Meglio così. Ora, abbiamo detto che l'algoritmo riconduce i casi difficili a casi più facili. Si dice che opera ricorsivamente, cioè chiama più volte sé stesso fino a che non è arrivato a un caso gestibile”.
“E qual è questo caso gestibile?”.
“Il caso è gestibile quando il numero di cui dobbiamo calcolare la radice quadrata è composto da al massimo tre cifre”.
“E perché è gestibile?”.
“Perché i quadrati composti da al più tre cifre non sono così tanti, e ce li possiamo calcolare a mano”.
“Cosa?”.
“Sì, hai capito bene: quando arriviamo a un numero composto da tre cifre o meno, diciamo al computer quale risultato deve dare”.
“Questo è barare, però”.
“Anche imparare le tabelline a memoria lo è, allora”.
“Uhm”.
“Rassegnati: inseriamo nel computer la lista di alcuni quadrati e, per loro, non ci poniamo più il problema di estrarre la radice quadrata”.
“Va bene, mi rassegno”.
“Ottimo. Ecco dunque una funzione, che si chiama BaseSqrtRem, che calcola le radici dei numeri composti da al massimo 3 cifre”.
“Oh, molto bene, cerco di capire cosa fa. Vedo intanto un controllo su m: deve effettivamente essere un numero di tre cifre”.
“Esatto”.
“Poi vedo che costruisci un dizionario in cui a ogni quadrato perfetto associ la sua radice”.
“Sì, come vedi non sono tanti. E anche nella realtà si fa così, eh. L'algoritmo memorizza una tabella di valori a cui fare riferimento: serve per terminare il ciclo ricorsivo”.
“Ok, mi fido, immagino che dopo si vedrà questo ciclo. Poi, vediamo che succede: fai un ciclo in cui esplori il dizionario ordinato. Perché lo ordini?”.
“Perché non è detto che i valori dentro a un dizionario python siano ordinati, e a noi invece interessa che lo siano. Per esempio, se vuoi calcolare la radice quadrata di 420 devi cominciare a guardare i valori che sono nella lista dei quadrati, e continui a scorrere la lista finché non trovi un numero che supera 420. Nel frattempo, memorizza l'ultimo valore che hai trovato”.
“In questo caso troverei 441”.
“Sì: il ciclo si blocca non appena trova 441, e in quel momento all'interno della variabile k è memorizzato il valore trovato al passo precedente, cioè 400”.
“Sì, vedo: il ciclo si blocca prima della assegnazione k = i”.
“Perfetto. Ora vedi che si esce dal ciclo e che si memorizza in s il valore di d[400], cioè 20”.
“Questa è la radice di 420, vero?”.
“Sì. Poi viene calcolato il resto sottraendo da 420 il quadrato di s, cioè 400. Risultato: 20”.
“Quindi la radice quadrata di 420 è 20 col resto di 20”.
“Perfetto, e questo è il caso base: quando arriviamo qui sappiamo fare il calcolo”.
“Perché nella lista c'è anche 1024?”.
“Perché se vuoi calcolare la radice di un numero maggiore o uguale a 961 il ciclo deve arrivare a considerare 1024, per poi bloccarsi”.
“Ok, chiaro. E adesso?”.
“Adesso arriva la parte seria: la funzione SqrtRem. L'idea è questa: se ho un numero composto da 4 cifre o più, lo prendo e divido le cifre in quattro gruppetti”.
“Anche nel calcolo a mano facevamo così? Non mi pare”.
“No, facevamo una cosa analoga ma non identica: dividevamo il numero a gruppetti composti da 2 cifre: tenevamo fisso il numero di cifre di cui era composto ogni gruppetto, e in questo modo avevamo un numero di gruppetti variabile”.
“Qui invece teniamo fisso il numero di gruppetti, mentre facciamo variare il numero di cifre che li compongono?”.
“Proprio così. Ti faccio vedere la parte di funzione che si occupa di questa suddivisione:”.
“Ah, ma usi le stringhe?”.
“Sì, ti ho detto che questo programma è un esempio, che in realtà non si fa così, no?”.
“Sì, ma non capisco le stringhe”.
“Immagina di fare i conti a mano: quando dividi un numero in 4 gruppi, lo fai contando le cifre. Tu, operatore manuale, usi le stringhe in questa fase, non ragioni sui valori numerici. Il programma ti copia”.
“Ah, va bene”.
“Quindi, arrivati alla fine di questa parte, nelle quattro variabili a0, a1, a2 e a3 sono contenuti i quattro gruppetti di cifre”.
“E che succede se la divisione non è esatta?”.
“Le cifre in più vanno a finire in a0. Mi spiego meglio: se il numero di cui vuoi calcolare la radice è 12345, i gruppi vengono composti in questo modo: 12|3|4|5. Se invece fosse 123456, i gruppi diventerebbero 123|4|5|6”.
“Ah, ok. Diventano tutti di 2 cifre quando si arriva a 12345678, suppongo”.
“Proprio così. Ora si parte con l'algoritmo vero e proprio, usando la filosofia divide and conquer”.
“Cioè?”.
“Cioè calcoliamo la radice quadrata del numero composto solo dai primi due gruppetti, che sono a0 e a1”.
“E come facciamo?”.
“Richiamiamo la funzione con quel numero”.
“Roba da matti. E funziona?”.
“Certo che funziona: ogni volta accorci il numero di cui vuoi calcolare la radice, e a un certo punto arrivi a un numero composto da al massimo 3 cifre. E di quello sai calcolare la radice. Il difficile è poi tornare indietro e ricomporre, da tutti i pezzettini, la radice del numero iniziale”.
“Ah, ecco”.
“Ecco quindi il nucleo della funzione che calcola la radice quadrata”.
“Oh, qua non si capisce niente”.
“Allora, la prima riga è la chiamata ricorsiva: vedi che viene chiamata nuovamente SqrtRem passandole, però, il numero a3*10^l+a2, cioè il numero composto dai primi due gruppetti di cifre”.
“Perché elevi alla l?”.
“Perché l è il numero di cifre di cui è composto ogni gruppetto: moltiplicare per 10l significa spostare di l cifre a sinistra il numero moltiplicato”.
“Ah, ok. Immagino che nella realtà al posto di 10 ci sia un 2, vero?”.
“Esatto”.
“Quindi dentro a s1 e r1 ci finiranno la radice quadrata e il resto di quel numero”.
“Sì, e ora bisogna mettere a posto i conti, perché così facendo non hai considerato le cifre contenute in a1 e a0”.
“E come si fa?”.
“Forse è meglio seguire i calcoli con un esempio: diciamo che vogliamo calcolare la radice di 12345”.
“Oh, bene, un esempio con dei numeri veri! Allora, divido in quattro gruppetti, che dovrebbero essere questi: 12|3|4|5”.
“Giusto. Ora prendiamo soltanto i primi due, cioè il numero 123, e riapplichiamo di nuovo l'algoritmo”.
“Questa volta però il numero è di 3 cifre, quindi dovremmo trovare il risultato direttamente, vero?”.
“Certo: prova a farlo a mente. Qual è il più grande quadrato minore di 123?”.
“121, il quadrato di 11”.
“Bene, quindi 123 = 112 + 2”.
“Ah, quindi ho trovato s1 = 11 e r1 = 2, vero?”.
“Sì, questo è il primo passo: quello che hai fatto è scrivere 12300 = 12100 + 200. Ma tu vuoi trovare un'espressione simile per 12345”.
“Ho completamente trascurato le cifre 4 e 5”.
“Già. Ora procediamo come si farebbe a mano: se ricordi, c'era un calcolo apparentemente magico che diceva di raddoppiare il risultato parziale trovato fino a questo momento per la radice, per poi eseguire altri calcoli che avevano lo scopo di trovare la cifra successiva”.
“Mi ricordo, avevi spiegato anche il perché”.
“Ottimo. Partiamo sempre dalla stessa idea: una prima stima della radice che stiamo calcolando è 110, ma è soggetta a errore perché siamo partiti da 12300. Magari il numero che vogliamo non è 110 ma 111, o 112”.
“Allora modifichiamo un po' quel 110”.
“Esatto: immagina che sia (110 + q). Se lo elevi al quadrato ottieni 12100 + 220q + q2”.
“E quindi 220q + q2 dovrebbe essere uguale a 12345”.
“Ma tu hai già scritto 12345 come 12100 + 200 + un errore, che è 45. Ora si procede in modo un po' diverso rispetto a quello che si farebbe a mano: si corregge 200 non aggiungendo 45 ma solo 40. Cioè, in realtà non si fa il confronto tra 245 e 220q ma tra 24 e 22q, buttando via l'ultima cifra”.
“Perché? Non considero nemmeno q2? Nel calcolo a mano lo facevamo”.
“Hai ragione, qua non si fa, e non ho trovato una spiegazione sul motivo. Alla fine l'errore che si commette trascurando quel termine viene corretto, ma non so perché si preferisca fare così. Sospetto per la velocità di esecuzione: se confrontiamo 240 con 220q vediamo che ci basta fare una divisione per trovare q, senza procedere per tentativi. Se si commette un errore, alla fine lo si corregge”.
“Ah, ok, quindi avremmo che q = 24/22, cioè 1”.
“Sì, con resto di 2. Questi due valori vengono memorizzati in q e u”.
“Ah, ecco il motivo di quelle due righe di codice. E poi che succede?”.
“Le due righe successive aggiungono la cifra q al risultato, e ricalcolano il resto”.
“E quel controllo sul resto negativo?”.
“Eh, è la correzione di cui ti parlavo prima: i calcoli fatti per q potrebbero, in alcuni casi, dare un resto negativo. Se così fosse, allora diminuiamo s di 1 e aggiorniamo il resto”.
“Non capisco bene l'aggiornamento del resto”.
“Supponi di aver sbagliato per eccesso il calcolo di una radice, cioè come se tu scrivessi A = B2 − r”.
“Ah, ok, devo sottrarre il resto invece di aggiungerlo”.
“Esatto. Ora, che succede se al posto di B metti B − 1? Come devi correggere l'uguaglianza?”.
“Provo a fare i calcoli: se sviluppo il quadrato del binomio ottengo (B − 1)2 = B2 − 2B + 1”.
“E quindi A = (B − 1)2 + 2B − 1 + r”.
“Ah, ecco, vedo: al vecchio resto devo aggiungere 2B e togliere 1, ho capito”.
“Perfetto. Ecco qua la funzione completa che calcola la radice quadrata di un numero col resto”.
“Ottimo. Ancora una vittoria per la carta e la penna”.
“Ricordo. Una radice quadrata con resto, se ben ricordo”.
“Esatto. Per essere precisi: dato un numero m, diciamo che s è la sua radice quadrata e r è il resto se valgono queste relazioni:”.
s2 ≤ m = s2 + r < (s + 1)2
“E abbiamo detto che i computer seguono un algoritmo simile”.
“Ancora esatto: adattano questo algoritmo alle loro caratteristiche, sfruttano la base 2 invece della base 10, e sfruttano soprattutto il fatto di essere molto bravi a compiere operazioni ripetitive. In sostanza imparano a fare i calcoli con un caso relativamente facile, e se poi i numeri diventano troppo grossi allora li spezzettano in modo da ridurre il caso difficile a tanti casi facili”.
“Bello”.
“Posso farti vedere un programmino che simula quello che viene fatto effettivamente dall'algoritmo”.
“Perché dici simula?”.
“Perché le vere implementazioni sono al solito complicate da casi particolari relativi a quanto sono lunghi i gruppi di bit che ogni macchina riesce a gestire velocemente, e quindi i veri sorgenti sono pieni di controlli del tipo se lavori con 32 bit allora fai questo, se invece lavori con 64 allora fai quest'altro, e cose così”.
“Roba da informatici”.
“Già. E poi, per semplicità, il mio programmino funziona in base 10”.
“Ok”.
“L'algoritmo si chiama SqrtRem”.
“Bel nome, molto evocativo”.
“Non l'ho scelto io: è il nome che gli autori della libreria GMP hanno scelto; la prima parte, Sqrt, significa Square Root, cioè radice quadrata, e la seconda, Rem, sta per remainder, cioè resto”.
“Va bene, non critico più i nomi scelti dagli informatici”.
“Meglio così. Ora, abbiamo detto che l'algoritmo riconduce i casi difficili a casi più facili. Si dice che opera ricorsivamente, cioè chiama più volte sé stesso fino a che non è arrivato a un caso gestibile”.
“E qual è questo caso gestibile?”.
“Il caso è gestibile quando il numero di cui dobbiamo calcolare la radice quadrata è composto da al massimo tre cifre”.
“E perché è gestibile?”.
“Perché i quadrati composti da al più tre cifre non sono così tanti, e ce li possiamo calcolare a mano”.
“Cosa?”.
“Sì, hai capito bene: quando arriviamo a un numero composto da tre cifre o meno, diciamo al computer quale risultato deve dare”.
“Questo è barare, però”.
“Anche imparare le tabelline a memoria lo è, allora”.
“Uhm”.
“Rassegnati: inseriamo nel computer la lista di alcuni quadrati e, per loro, non ci poniamo più il problema di estrarre la radice quadrata”.
“Va bene, mi rassegno”.
“Ottimo. Ecco dunque una funzione, che si chiama BaseSqrtRem, che calcola le radici dei numeri composti da al massimo 3 cifre”.
“Oh, molto bene, cerco di capire cosa fa. Vedo intanto un controllo su m: deve effettivamente essere un numero di tre cifre”.
“Esatto”.
“Poi vedo che costruisci un dizionario in cui a ogni quadrato perfetto associ la sua radice”.
“Sì, come vedi non sono tanti. E anche nella realtà si fa così, eh. L'algoritmo memorizza una tabella di valori a cui fare riferimento: serve per terminare il ciclo ricorsivo”.
“Ok, mi fido, immagino che dopo si vedrà questo ciclo. Poi, vediamo che succede: fai un ciclo in cui esplori il dizionario ordinato. Perché lo ordini?”.
“Perché non è detto che i valori dentro a un dizionario python siano ordinati, e a noi invece interessa che lo siano. Per esempio, se vuoi calcolare la radice quadrata di 420 devi cominciare a guardare i valori che sono nella lista dei quadrati, e continui a scorrere la lista finché non trovi un numero che supera 420. Nel frattempo, memorizza l'ultimo valore che hai trovato”.
“In questo caso troverei 441”.
“Sì: il ciclo si blocca non appena trova 441, e in quel momento all'interno della variabile k è memorizzato il valore trovato al passo precedente, cioè 400”.
“Sì, vedo: il ciclo si blocca prima della assegnazione k = i”.
“Perfetto. Ora vedi che si esce dal ciclo e che si memorizza in s il valore di d[400], cioè 20”.
“Questa è la radice di 420, vero?”.
“Sì. Poi viene calcolato il resto sottraendo da 420 il quadrato di s, cioè 400. Risultato: 20”.
“Quindi la radice quadrata di 420 è 20 col resto di 20”.
“Perfetto, e questo è il caso base: quando arriviamo qui sappiamo fare il calcolo”.
“Perché nella lista c'è anche 1024?”.
“Perché se vuoi calcolare la radice di un numero maggiore o uguale a 961 il ciclo deve arrivare a considerare 1024, per poi bloccarsi”.
“Ok, chiaro. E adesso?”.
“Adesso arriva la parte seria: la funzione SqrtRem. L'idea è questa: se ho un numero composto da 4 cifre o più, lo prendo e divido le cifre in quattro gruppetti”.
“Anche nel calcolo a mano facevamo così? Non mi pare”.
“No, facevamo una cosa analoga ma non identica: dividevamo il numero a gruppetti composti da 2 cifre: tenevamo fisso il numero di cifre di cui era composto ogni gruppetto, e in questo modo avevamo un numero di gruppetti variabile”.
“Qui invece teniamo fisso il numero di gruppetti, mentre facciamo variare il numero di cifre che li compongono?”.
“Proprio così. Ti faccio vedere la parte di funzione che si occupa di questa suddivisione:”.
“Ah, ma usi le stringhe?”.
“Sì, ti ho detto che questo programma è un esempio, che in realtà non si fa così, no?”.
“Sì, ma non capisco le stringhe”.
“Immagina di fare i conti a mano: quando dividi un numero in 4 gruppi, lo fai contando le cifre. Tu, operatore manuale, usi le stringhe in questa fase, non ragioni sui valori numerici. Il programma ti copia”.
“Ah, va bene”.
“Quindi, arrivati alla fine di questa parte, nelle quattro variabili a0, a1, a2 e a3 sono contenuti i quattro gruppetti di cifre”.
“E che succede se la divisione non è esatta?”.
“Le cifre in più vanno a finire in a0. Mi spiego meglio: se il numero di cui vuoi calcolare la radice è 12345, i gruppi vengono composti in questo modo: 12|3|4|5. Se invece fosse 123456, i gruppi diventerebbero 123|4|5|6”.
“Ah, ok. Diventano tutti di 2 cifre quando si arriva a 12345678, suppongo”.
“Proprio così. Ora si parte con l'algoritmo vero e proprio, usando la filosofia divide and conquer”.
“Cioè?”.
“Cioè calcoliamo la radice quadrata del numero composto solo dai primi due gruppetti, che sono a0 e a1”.
“E come facciamo?”.
“Richiamiamo la funzione con quel numero”.
“Roba da matti. E funziona?”.
“Certo che funziona: ogni volta accorci il numero di cui vuoi calcolare la radice, e a un certo punto arrivi a un numero composto da al massimo 3 cifre. E di quello sai calcolare la radice. Il difficile è poi tornare indietro e ricomporre, da tutti i pezzettini, la radice del numero iniziale”.
“Ah, ecco”.
“Ecco quindi il nucleo della funzione che calcola la radice quadrata”.
“Oh, qua non si capisce niente”.
“Allora, la prima riga è la chiamata ricorsiva: vedi che viene chiamata nuovamente SqrtRem passandole, però, il numero a3*10^l+a2, cioè il numero composto dai primi due gruppetti di cifre”.
“Perché elevi alla l?”.
“Perché l è il numero di cifre di cui è composto ogni gruppetto: moltiplicare per 10l significa spostare di l cifre a sinistra il numero moltiplicato”.
“Ah, ok. Immagino che nella realtà al posto di 10 ci sia un 2, vero?”.
“Esatto”.
“Quindi dentro a s1 e r1 ci finiranno la radice quadrata e il resto di quel numero”.
“Sì, e ora bisogna mettere a posto i conti, perché così facendo non hai considerato le cifre contenute in a1 e a0”.
“E come si fa?”.
“Forse è meglio seguire i calcoli con un esempio: diciamo che vogliamo calcolare la radice di 12345”.
“Oh, bene, un esempio con dei numeri veri! Allora, divido in quattro gruppetti, che dovrebbero essere questi: 12|3|4|5”.
“Giusto. Ora prendiamo soltanto i primi due, cioè il numero 123, e riapplichiamo di nuovo l'algoritmo”.
“Questa volta però il numero è di 3 cifre, quindi dovremmo trovare il risultato direttamente, vero?”.
“Certo: prova a farlo a mente. Qual è il più grande quadrato minore di 123?”.
“121, il quadrato di 11”.
“Bene, quindi 123 = 112 + 2”.
“Ah, quindi ho trovato s1 = 11 e r1 = 2, vero?”.
“Sì, questo è il primo passo: quello che hai fatto è scrivere 12300 = 12100 + 200. Ma tu vuoi trovare un'espressione simile per 12345”.
“Ho completamente trascurato le cifre 4 e 5”.
“Già. Ora procediamo come si farebbe a mano: se ricordi, c'era un calcolo apparentemente magico che diceva di raddoppiare il risultato parziale trovato fino a questo momento per la radice, per poi eseguire altri calcoli che avevano lo scopo di trovare la cifra successiva”.
“Mi ricordo, avevi spiegato anche il perché”.
“Ottimo. Partiamo sempre dalla stessa idea: una prima stima della radice che stiamo calcolando è 110, ma è soggetta a errore perché siamo partiti da 12300. Magari il numero che vogliamo non è 110 ma 111, o 112”.
“Allora modifichiamo un po' quel 110”.
“Esatto: immagina che sia (110 + q). Se lo elevi al quadrato ottieni 12100 + 220q + q2”.
“E quindi 220q + q2 dovrebbe essere uguale a 12345”.
“Ma tu hai già scritto 12345 come 12100 + 200 + un errore, che è 45. Ora si procede in modo un po' diverso rispetto a quello che si farebbe a mano: si corregge 200 non aggiungendo 45 ma solo 40. Cioè, in realtà non si fa il confronto tra 245 e 220q ma tra 24 e 22q, buttando via l'ultima cifra”.
“Perché? Non considero nemmeno q2? Nel calcolo a mano lo facevamo”.
“Hai ragione, qua non si fa, e non ho trovato una spiegazione sul motivo. Alla fine l'errore che si commette trascurando quel termine viene corretto, ma non so perché si preferisca fare così. Sospetto per la velocità di esecuzione: se confrontiamo 240 con 220q vediamo che ci basta fare una divisione per trovare q, senza procedere per tentativi. Se si commette un errore, alla fine lo si corregge”.
“Ah, ok, quindi avremmo che q = 24/22, cioè 1”.
“Sì, con resto di 2. Questi due valori vengono memorizzati in q e u”.
“Ah, ecco il motivo di quelle due righe di codice. E poi che succede?”.
“Le due righe successive aggiungono la cifra q al risultato, e ricalcolano il resto”.
“E quel controllo sul resto negativo?”.
“Eh, è la correzione di cui ti parlavo prima: i calcoli fatti per q potrebbero, in alcuni casi, dare un resto negativo. Se così fosse, allora diminuiamo s di 1 e aggiorniamo il resto”.
“Non capisco bene l'aggiornamento del resto”.
“Supponi di aver sbagliato per eccesso il calcolo di una radice, cioè come se tu scrivessi A = B2 − r”.
“Ah, ok, devo sottrarre il resto invece di aggiungerlo”.
“Esatto. Ora, che succede se al posto di B metti B − 1? Come devi correggere l'uguaglianza?”.
“Provo a fare i calcoli: se sviluppo il quadrato del binomio ottengo (B − 1)2 = B2 − 2B + 1”.
“E quindi A = (B − 1)2 + 2B − 1 + r”.
“Ah, ecco, vedo: al vecchio resto devo aggiungere 2B e togliere 1, ho capito”.
“Perfetto. Ecco qua la funzione completa che calcola la radice quadrata di un numero col resto”.
“Ottimo. Ancora una vittoria per la carta e la penna”.
lunedì 2 aprile 2018
Come fanno i computer a calcolare le radici quadrate? — Parte 1: calcolo manuale
“La risposta breve è: le calcolano come faremmo noi per calcolarle a mano”.
“Ah, certo, tutti calcolano radici a mano”.
“La mia professoressa delle medie mi insegnò a farlo, sai?”.
“Anche la mia, ma se devo dire che mi ricordo come si fa, direi una bugia”.
“Sì, il procedimento non è per niente intuitivo, soprattutto in una parte. Ma partiamo dall'inizio: la descrizione completa dell'algoritmo l'ha scritta .mau. un po' di tempo fa, ed è spiegata qua”.
“Oh, bene, bene, ora me la guardo. No, decisamente non mi ricordavo tutto. Anzi, posso dire che mi ricordavo solo che si dovevano raggruppare le cifre del numero a due a due”.
“Sì, quello è il punto di partenza. Vogliamo provare a calcolare una radice quadrata a mano, in modo da sottolineare i punti importanti del procedimento?”.
“Ok, andiamo”.
“Allora, proviamo a calcolare la radice di 7654. Scriviamo il numero raggruppando le cifre a due a due”.
“E quindi formiamo due gruppetti”.
“Sì, e scriviamo in questo modo il tutto:”.
“Ok, ora che succede?”.
“Ora si prendono le prime due cifre e si dà per scontato che la radice del numero composto solo da quelle due cifre la sappiamo calcolare”.
“Io non so quanto valga esattamente la radice di 76, però”.
“Sei in buona compagnia: nessuno lo sa. Ma non ci serve una precisione infinita, perché lavoriamo solo sui numeri interi: per calcolare la radice di 76 ti serve soltanto conoscere le tabelline”.
“Ah, allora posso dire che 8 è troppo poco e 9 è troppo”.
“Approssimiamo per difetto”.
“Allora dico che la radice di 76 è 8”.
“Benissimo, il primo passo è fatto, scriviamo 8 come prima cifra”.
“Fin qua è stato facile”.
“Ora correggiamo l'errore: calcoliamo il vero quadrato di 8…”.
“Che è 64”.
“Lo scriviamo sotto al 76, e facciamo la differenza, in modo da trovare il resto”.
“Bene. Adesso? Non ricordo più come si va avanti”.
“Adesso c'è la parte magica del procedimento, ma prima di raccontarla vediamo quello che abbiamo fatto finora. In sostanza abbiamo capito che 76 = 82 + 12”.
“D'accordo”.
“Ma 76 è stato estratto dal numero 7654 prendendo le prime due cifre, e quindi quello che abbiamo fatto in realtà è stato capire che 7600 = 82 × 102 + 1200”.
“Va bene, hai moltiplicato tutto per cento”.
“Sì, in questo modo abbiamo calcolato la radice di 7600, con il suo resto. Però volevamo calcolare la radice di 7654, che è un po' più grande”.
“Ci basterà correggere il resto: 7654 = 82 × 102 + 1254”.
“Ah, certo, ma così il resto diventa un po' troppo grande: non possiamo fare di meglio?”.
“Non saprei. Cioè, immagino di sì, ma non so mica come”.
“Quell'80 è un po' troppo basso, se lo aumentiamo un pochino magari riusciamo a diminuire il resto”.
“Vero, se prendo ad esempio 81 mi viene che 7654 = 812 + 1093”.
“Va già meglio, ma hai scelto 81 a caso. Magari con 82 può andare meglio, o forse con 83, o chissà”.
“E come faccio?”.
“Prova a fare una stima: invece di usare 80, tu vuoi usare 80 + t”.
“E quanto vale t?”.
“Ancora non lo sai: è quello che vuoi stimare. Prova a scrivere 7654 come quadrato di 80 + t. Anzi, per maggiore generalità scrivi 8 × 10 + t”.
“Va bene: 7654 = (8 × 10 + t)2. E adesso?”.
“Adesso svolgi il quadrato di binomio, lasciando indicati tutti i calcoli”.
“Oh, vediamo: quadrato del primo termine, doppio prodotto, quadrato del secondo… Mi viene questa roba:”.
7654 = 802 + 2 × 8 × 10 × t + t2.
“Ottimo. 802 fa 6400, è un numero che avevi già calcolato nel primo passo dell'algoritmo del calcolo della radice quadrata. La parte interessante è quella che segue: 2 × 8 × 10 × t + t2”.
“Che deve dare il famoso 1254”.
“Proprio così. Scriviamolo per bene:”.
2 × 8 × 10 × t + t2 = 1254.
“Ok, e adesso?”.
“Raccogliendo a fattor comune t si ottiene”.
(2 × 8 × 10 + t) × t = 1254
“Bene, e questo mi aiuta a trovare t?”.
“Questo spiega il passaggio magico dell'algoritmo della radice quadrata. Ricordi che avevi trovato la prima cifra, 8?”.
“Sì, e l'avevo scritta in alto”.
“Bene. Adesso il procedimento dice: abbassa altre due cifre di 7654, e poi raddoppia le cifre che hai trovato provvisoriamente per la radice quadrata, scrivile sotto, in questo modo…”.
“E poi?”.
“E poi trasforma 16 in decine, e trova quella cifra t delle unità da aggiungere a 16 in modo da trovare un numero 16t tale che 16t × t sia il più vicino possibile a 1254, senza però superarlo”.
“Ma quando scrivi 16t non intendi 16 × t, vero?”.
“No, è per questo che ho sempre esplicitato il simbolo di moltiplicazione: in questo caso con 16t intendo un numero di tre cifre avente 1 come cifra delle centinaia, 6 come cifra delle decine, e t come cifra delle unità”.
“E come si fa a trovare quel numero?”.
“Lo spiega sempre .mau.: in sostanza si va per tentativi, facendo una stima grossolana per eccesso e poi scendendo. Avevamo trovato un resto parziale di 12, dopo aver scritto il primo 8”.
“Vero”.
“Ora, 12 sono diventate centinaia, e la cifra delle decine è diventata 5”.
“Sì, poi 4 è quella delle unità, in modo da ottenere 1254”.
“Tieni solo le prime 3, cioè 125”.
“Ok”.
“Adesso calcola 125 / 16”.
“Viene 7.8 e rotti”.
“Parti quindi da 8, e fai 168 × 8, scrivendolo nello spazio vuoto sotto a 8”.
“Così?”.
“Sì: come vedi 1344 è un numero maggiore di 1254”.
“Allora?”.
“Allora la stima t = 8 era troppo alta, abbassala di uno e ripeti il procedimento”.
“Questo va bene, ora puoi scrivere 1169 sotto a 1254 e calcolare il resto giusto. E non dimenticare di aggiungere la cifra 7 al risultato della radice, in alto, di fianco all'8”.
“Ecco:”.
“Perfetto, fine del procedimento. La radice di 7654 è 87 con resto di 83”.
“Fammi capire meglio questa cosa del resto, che non l'avevo mai sentito associato alle radici quadrate”.
“Quello che abbiamo fatto è questo: dato m, numero intero positivo, lo abbiamo scritto così”.
m = s2 + r
“Ah, dove s è la radice quadrata approssimata per difetto”.
“E r è il resto, esatto. Nel nostro caso 7654 = 872 + 83”.
“Ho capito”.
“Il procedimento per fare il calcolo a mano è quello di fare i conti a pezzi, dando per scontato che riusciamo a calcolare a mente le radici dei numeri di due cifre”.
“Ok”.
“La cosa strana è che per poter andare avanti e aggiungere una cifra occorre inserire una strana moltiplicazione per 2, che non si sa bene da dove salti fuori”.
“Quando abbiamo preso l'8 appena scritto e lo abbiamo fatto diventare 16?”.
“Proprio così. La spiegazione di quella parte è che quella moltiplicazione per 2 corrisponde al famoso doppio prodotto che salta fuori nello sviluppo del quadrato del binomio”.
“Che roba”.
“E quindi la prossima cifra l'abbiamo cercata intorno all'approssimazione 125 diviso per il doppio prodotto, cioè 125 / 16”.
“Avremmo dovuto fare 1254 / 167”.
“Certo, ma quel 7 non lo conoscevamo ancora…”.
“Ah, già, è vero! E quindi abbiamo stimato 1254 / 16t facendo 125 / 16”.
“Sì, e poi abbiamo aggiustato il tiro”.
“E dici che i computer fanno la stessa cosa?”.
“Non so se tutti i computer facciano così, ma questo è l'algoritmo usato dalla libreria GMP: GNU multiple precision arithmetic library”.
“Dalla descrizione presente nell'introduzione, sembra il meglio che possiamo avere per fare calcoli”.
“Pare proprio di sì: precisione multipla, massima velocità. L'algoritmo usato dalla libreria è in realtà una generalizzazione di questo, ma si basa su questi identici concetti: prendo un numero arbitrariamente grande e lo spezzetto fino a che non so fare i calcoli”.
“A gruppi di 2 cifre?”.
“Non esattamente, ma lo vediamo in dettaglio la prossima volta. Per ora accontentiamoci di definire bene quello che vogliamo fare”.
“La radice quadrata, no?”.
“Certo, ma come definiamo per bene il resto? Quanto può essere grande al massimo?”.
“Ehm”.
“Vedi che occorre, prima di tutto, capire quello che vogliamo. Allora, dato un numero m, diciamo che s è la sua radice quadrata e r è il resto se valgono queste relazioni:”.
s2 ≤ m = s2 + r < (s + 1)2
“Ok, credo di aver capito, il resto non deve essere così grande da farmi arrivare al quadrato successivo”.
“Esatto”.
“Ah, certo, tutti calcolano radici a mano”.
“La mia professoressa delle medie mi insegnò a farlo, sai?”.
“Anche la mia, ma se devo dire che mi ricordo come si fa, direi una bugia”.
“Sì, il procedimento non è per niente intuitivo, soprattutto in una parte. Ma partiamo dall'inizio: la descrizione completa dell'algoritmo l'ha scritta .mau. un po' di tempo fa, ed è spiegata qua”.
“Oh, bene, bene, ora me la guardo. No, decisamente non mi ricordavo tutto. Anzi, posso dire che mi ricordavo solo che si dovevano raggruppare le cifre del numero a due a due”.
“Sì, quello è il punto di partenza. Vogliamo provare a calcolare una radice quadrata a mano, in modo da sottolineare i punti importanti del procedimento?”.
“Ok, andiamo”.
“Allora, proviamo a calcolare la radice di 7654. Scriviamo il numero raggruppando le cifre a due a due”.
“E quindi formiamo due gruppetti”.
“Sì, e scriviamo in questo modo il tutto:”.
76.54 |
|-------
|
“Ok, ora che succede?”.
“Ora si prendono le prime due cifre e si dà per scontato che la radice del numero composto solo da quelle due cifre la sappiamo calcolare”.
“Io non so quanto valga esattamente la radice di 76, però”.
“Sei in buona compagnia: nessuno lo sa. Ma non ci serve una precisione infinita, perché lavoriamo solo sui numeri interi: per calcolare la radice di 76 ti serve soltanto conoscere le tabelline”.
“Ah, allora posso dire che 8 è troppo poco e 9 è troppo”.
“Approssimiamo per difetto”.
“Allora dico che la radice di 76 è 8”.
“Benissimo, il primo passo è fatto, scriviamo 8 come prima cifra”.
76.54 | 8
|-------
|
“Fin qua è stato facile”.
“Ora correggiamo l'errore: calcoliamo il vero quadrato di 8…”.
“Che è 64”.
“Lo scriviamo sotto al 76, e facciamo la differenza, in modo da trovare il resto”.
76.54 | 8 64 |------- -- | 12 |
“Bene. Adesso? Non ricordo più come si va avanti”.
“Adesso c'è la parte magica del procedimento, ma prima di raccontarla vediamo quello che abbiamo fatto finora. In sostanza abbiamo capito che 76 = 82 + 12”.
“D'accordo”.
“Ma 76 è stato estratto dal numero 7654 prendendo le prime due cifre, e quindi quello che abbiamo fatto in realtà è stato capire che 7600 = 82 × 102 + 1200”.
“Va bene, hai moltiplicato tutto per cento”.
“Sì, in questo modo abbiamo calcolato la radice di 7600, con il suo resto. Però volevamo calcolare la radice di 7654, che è un po' più grande”.
“Ci basterà correggere il resto: 7654 = 82 × 102 + 1254”.
“Ah, certo, ma così il resto diventa un po' troppo grande: non possiamo fare di meglio?”.
“Non saprei. Cioè, immagino di sì, ma non so mica come”.
“Quell'80 è un po' troppo basso, se lo aumentiamo un pochino magari riusciamo a diminuire il resto”.
“Vero, se prendo ad esempio 81 mi viene che 7654 = 812 + 1093”.
“Va già meglio, ma hai scelto 81 a caso. Magari con 82 può andare meglio, o forse con 83, o chissà”.
“E come faccio?”.
“Prova a fare una stima: invece di usare 80, tu vuoi usare 80 + t”.
“E quanto vale t?”.
“Ancora non lo sai: è quello che vuoi stimare. Prova a scrivere 7654 come quadrato di 80 + t. Anzi, per maggiore generalità scrivi 8 × 10 + t”.
“Va bene: 7654 = (8 × 10 + t)2. E adesso?”.
“Adesso svolgi il quadrato di binomio, lasciando indicati tutti i calcoli”.
“Oh, vediamo: quadrato del primo termine, doppio prodotto, quadrato del secondo… Mi viene questa roba:”.
7654 = 802 + 2 × 8 × 10 × t + t2.
“Ottimo. 802 fa 6400, è un numero che avevi già calcolato nel primo passo dell'algoritmo del calcolo della radice quadrata. La parte interessante è quella che segue: 2 × 8 × 10 × t + t2”.
“Che deve dare il famoso 1254”.
“Proprio così. Scriviamolo per bene:”.
2 × 8 × 10 × t + t2 = 1254.
“Ok, e adesso?”.
“Raccogliendo a fattor comune t si ottiene”.
(2 × 8 × 10 + t) × t = 1254
“Bene, e questo mi aiuta a trovare t?”.
“Questo spiega il passaggio magico dell'algoritmo della radice quadrata. Ricordi che avevi trovato la prima cifra, 8?”.
“Sì, e l'avevo scritta in alto”.
“Bene. Adesso il procedimento dice: abbassa altre due cifre di 7654, e poi raddoppia le cifre che hai trovato provvisoriamente per la radice quadrata, scrivile sotto, in questo modo…”.
76.54 | 8 64 |------- ----- | 16 12.54 |
“E poi?”.
“E poi trasforma 16 in decine, e trova quella cifra t delle unità da aggiungere a 16 in modo da trovare un numero 16t tale che 16t × t sia il più vicino possibile a 1254, senza però superarlo”.
“Ma quando scrivi 16t non intendi 16 × t, vero?”.
“No, è per questo che ho sempre esplicitato il simbolo di moltiplicazione: in questo caso con 16t intendo un numero di tre cifre avente 1 come cifra delle centinaia, 6 come cifra delle decine, e t come cifra delle unità”.
“E come si fa a trovare quel numero?”.
“Lo spiega sempre .mau.: in sostanza si va per tentativi, facendo una stima grossolana per eccesso e poi scendendo. Avevamo trovato un resto parziale di 12, dopo aver scritto il primo 8”.
“Vero”.
“Ora, 12 sono diventate centinaia, e la cifra delle decine è diventata 5”.
“Sì, poi 4 è quella delle unità, in modo da ottenere 1254”.
“Tieni solo le prime 3, cioè 125”.
“Ok”.
“Adesso calcola 125 / 16”.
“Viene 7.8 e rotti”.
“Parti quindi da 8, e fai 168 × 8, scrivendolo nello spazio vuoto sotto a 8”.
“Così?”.
76.54 | 8 64 |--------------- ----- | 168 × 8 = 1344 12.54 |
“Sì: come vedi 1344 è un numero maggiore di 1254”.
“Allora?”.
“Allora la stima t = 8 era troppo alta, abbassala di uno e ripeti il procedimento”.
76.54 | 8 64 |--------------- ----- | 168 × 8 = 1344 12.54 | 167 × 7 = 1169
“Questo va bene, ora puoi scrivere 1169 sotto a 1254 e calcolare il resto giusto. E non dimenticare di aggiungere la cifra 7 al risultato della radice, in alto, di fianco all'8”.
“Ecco:”.
76.54 | 87 64 |--------------- ----- | 168 × 8 = 1344 12.54 | 167 × 7 = 1169 11.69 | ----- | 83 |
“Perfetto, fine del procedimento. La radice di 7654 è 87 con resto di 83”.
“Fammi capire meglio questa cosa del resto, che non l'avevo mai sentito associato alle radici quadrate”.
“Quello che abbiamo fatto è questo: dato m, numero intero positivo, lo abbiamo scritto così”.
m = s2 + r
“Ah, dove s è la radice quadrata approssimata per difetto”.
“E r è il resto, esatto. Nel nostro caso 7654 = 872 + 83”.
“Ho capito”.
“Il procedimento per fare il calcolo a mano è quello di fare i conti a pezzi, dando per scontato che riusciamo a calcolare a mente le radici dei numeri di due cifre”.
“Ok”.
“La cosa strana è che per poter andare avanti e aggiungere una cifra occorre inserire una strana moltiplicazione per 2, che non si sa bene da dove salti fuori”.
“Quando abbiamo preso l'8 appena scritto e lo abbiamo fatto diventare 16?”.
“Proprio così. La spiegazione di quella parte è che quella moltiplicazione per 2 corrisponde al famoso doppio prodotto che salta fuori nello sviluppo del quadrato del binomio”.
“Che roba”.
“E quindi la prossima cifra l'abbiamo cercata intorno all'approssimazione 125 diviso per il doppio prodotto, cioè 125 / 16”.
“Avremmo dovuto fare 1254 / 167”.
“Certo, ma quel 7 non lo conoscevamo ancora…”.
“Ah, già, è vero! E quindi abbiamo stimato 1254 / 16t facendo 125 / 16”.
“Sì, e poi abbiamo aggiustato il tiro”.
“E dici che i computer fanno la stessa cosa?”.
“Non so se tutti i computer facciano così, ma questo è l'algoritmo usato dalla libreria GMP: GNU multiple precision arithmetic library”.
“Dalla descrizione presente nell'introduzione, sembra il meglio che possiamo avere per fare calcoli”.
“Pare proprio di sì: precisione multipla, massima velocità. L'algoritmo usato dalla libreria è in realtà una generalizzazione di questo, ma si basa su questi identici concetti: prendo un numero arbitrariamente grande e lo spezzetto fino a che non so fare i calcoli”.
“A gruppi di 2 cifre?”.
“Non esattamente, ma lo vediamo in dettaglio la prossima volta. Per ora accontentiamoci di definire bene quello che vogliamo fare”.
“La radice quadrata, no?”.
“Certo, ma come definiamo per bene il resto? Quanto può essere grande al massimo?”.
“Ehm”.
“Vedi che occorre, prima di tutto, capire quello che vogliamo. Allora, dato un numero m, diciamo che s è la sua radice quadrata e r è il resto se valgono queste relazioni:”.
s2 ≤ m = s2 + r < (s + 1)2
“Ok, credo di aver capito, il resto non deve essere così grande da farmi arrivare al quadrato successivo”.
“Esatto”.
martedì 13 marzo 2018
Insomma, pi greco
“Eccoci dunque al punto finale, la quadratura del cerchio”.
“Oh, bene”.
“Facciamo un riassunto di tutto quello che abbiamo detto finora”.
“Ottimo”.
“I numeri reali si dividono in due categorie: i numeri razionali, cioè le frazioni, e i numeri irrazionali”.
“Cioè tutti gli altri”.
“Esatto. Ora, anche gli irrazionali sono divisibili in due categorie: i numeri algebrici (di cui fanno parte anche i razionali) e i numeri trascendenti”.
“I numeri algebrici sono quelli che possono essere soluzioni di equazioni polinomiali, vero?”.
“Equazioni polinomiali a coefficienti interi, altrimenti tutti i numeri potrebbero essere soluzioni dell'equazione x = a, e fine della storia”.
“Giusto”.
“Invece i trascendenti non possono essere soluzioni di equazioni polinomiali a coefficienti interi”.
“E fin qua ci siamo”.
“Alcuni numeri algebrici, poi, sono costruibili”.
“Il che significa che sono costruibili con riga e compasso, vero?”.
“Sì. Con riga e compasso si possono costruire numeri che, a partire dall'unità, possono essere ottenuti con un numero finito di somme, sottrazioni, moltiplicazioni, divisioni, e estrazioni di radice quadrata”.
“E ora c'è pi greco”.
“Già. Il problema della quadratura del cerchio si traduce in questa domanda: usando solo riga e compasso è possibile costruire un quadrato avente la stessa area di un cerchio dato? Domanda che, in linguaggio aritmetico, diventa: pi greco è un numero costruibile?”.
“E la risposta è no”.
“La risposta è: pi greco è un numero trascendente, e quindi se non appartiene all'insieme dei numeri algebrici non può appartenere nemmeno all'insieme dei numeri costruibili, che è un sottoinsieme proprio degli algebrici. Ma la dimostrazione di questa affermazione è lunga e difficile”.
“Lo sospettavo”.
“Ricordi quando abbiamo dimostrato l'esistenza di un numero trascendente?”.
“Sì, abbiamo usato una proprietà dei trascendenti, se ben ricordo, che riguardava le approssimazioni che possiamo fare con le frazioni”.
“Esatto: il numero che abbiamo trovato può essere approssimato con frazioni del tipo m/n con precisione minore di 1/nk, per qualunque k”.
“Anche pi greco, quindi?”.
“Purtroppo no, per pi greco questo metodo non funziona. Bisogna generalizzarlo tanto”.
“Questo tanto mi inquieta”.
“Cominciamo con notare che π ed e, il numero di Nepero, sono strettamente legati”.
“Non sarà la solita storia della formula più bella della matematica?”.
“Eh, sì. Sappiamo che eiπ = −1”.
“Ok, e quindi?”.
“E quindi se riusciamo a dimostrare che ea, con a un qualunque numero algebrico, non può essere uguale a −1, siamo a posto”.
“Fammi capire”.
“Dato che sappiamo che eiπ è effettivamente uguale a −1, se riusciamo a dimostrare quel teorema possiamo concludere che iπ non è algebrico”.
“Quindi iπ è trascendente, ma come facciamo a togliere i?”.
“Beh, è facile, i è algebrico, perché è soluzione dell'equazione a coefficienti interi x2 + 1=0, e quindi se il prodotto iπ è trascendente, significa che π deve esserlo”.
“Ah, ecco! Ottimo, quindi in effetti abbiamo spostato il problema dallo studio di pi greco allo studio della funzione esponenziale, vero?”.
“Proprio così. Ora, facciamo un passo più semplice di quello che vorremmo, giusto per capire come funzionano le cose: dimostriamo che e è irrazionale. Ci ricordiamo che per la funzione esponenziale esiste una serie di potenze che converge a essa”.
“Ed ecco che entra in campo l'analisi…”.
“Sì, una dimostrazione di teoria dei numeri fatta con l'analisi: bella roba. Ricordi quale serie di potenze converge all'esponenziale?”.
“Era una serie facile, mi pare 1 + x + x2/2! + x3/3! + …”.
“Esatto. Ora, supponiamo per assurdo che e sia razionale, cioè una frazione. Questo vuol dire che se moltiplico questa fantomatica frazione per un numero sufficientemente grande, ottengo un numero intero”.
“Certamente”.
“Allora calcolo n!e1, con n sufficientemente grande da fare in modo che il denominatore se ne vada. E uso proprio lo sviluppo in serie di ex”.
“Va bene, aspetta che provo a capire. Se prendo la serie dell'esponenziale vedo che si semplificano tanti denominatori”.
“Quanti?”.
“Beh, sicuramente quelli fino a xn/n!”.
“Giusto; e ricorda che abbiamo posto x = 1. Che succede dopo quel termine?”.
“Eh, mi sa che rimane una frazione: 1/(n + 1). Anzi, non solo una, poi c'è 1/(n + 1)(n + 2), e così via”.
“Esatto. E quindi n!e non può essere un intero”.
“E quindi e non può essere razionale! Molto bello”.
“E ora un altro passo di analisi: quello che abbiamo dimostrato non è che esiste soltanto un caso in cui, moltiplicando la frazione che dovrebbe essere uguale a e, si ottiene un assurdo. Di casi come quello che ne sono infiniti, basta prendere il moltiplicatore sempre più grande”.
“D'accordo”.
“Ogni volta che moltiplichiamo l'espansione in serie di e otteniamo una prima parte intera, e poi una coda composta da tante frazioni aventi il numeratore uguale a 1, e il denominatore che diventa sempre più grande.”.
“Immagino che il passo di analisi sia fare diventare infinitamente grande quel denominatore”.
“Immagini bene. Quello che abbiamo fatto, detto in altri termini, è questo: abbiamo trovato due successioni fn e gn tali che la differenza fne − gn diventa sempre più piccola man mano che n diventa sempre più grande. Nel nostro caso, giusto per essere chiari, fn è uguale a n!, mentre gn è uguale a 1/(n + 1) + 1/(n + 1)(n + 2) + …”.
“Ok, ho capito”.
“Quindi questa è una tecnica per dimostrare che un numero è irrazionale: trovo due successioni con quelle proprietà, e sono a posto”.
“Bene”.
“Ora un altro passo: passiamo dalla dimostrazione di irrazionalità di e1 alla dimostrazione di irrazionalità di ea, con a razionale diverso da zero”.
“Procediamo sempre allo stesso modo, con quelle due successioni?”.
“Sì, ma ora dobbiamo farlo per il caso generale, dove l'esponente di e è variabile. E l'aiuto ci viene proprio dalle approssimazioni di Padé”.
“Oh”.
“Sì, dal fatto che ex può essere approssimata molto bene dal rapporto f(x)/g(x), eliminando il denominatore possiamo passare all'espressione g(x)ex − f(x), che diventa sempre più piccola all'aumentare del numero di termini con cui faccio l'approssimazione”.
“Mamma mia”.
“Uno studio super tecnico di come sono fatti i polinomi f(x) e g(x) porta alla dimostrazione dell'ultima affermazione”.
“Super tecnico?”.
“Sì, vengono espressi come funzioni integrali di altre funzioni, in modo da poter costruire delle disuguaglianze comode e utili”.
“Certo, comode e utili…”.
“L'analisi è la matematica delle disuguaglianze: tutto è stima”.
“Andiamo bene”.
“Ti faccio solo un esempio, giusto per darti un'idea del livello: l'approssimazione di Padé di ordine 8 per la funzione esponenziale è questa: ”.
(x8 − 72x7 + 2520x6 − 55440x5 + 831600x4 − 8648640x3 + 60540480x2 − 259459200x + 518918400) / (x8 + 72x7 + 2520x6 + 55440x5 + 831600x4 + 8648640x3 + 60540480x2 + 259459200x + 518918400)
“Argh”.
“Che corrisponde a questa bella formuletta:”.
“Orrore”.
“Dove f(x) è il denominatore della frazione enorme che ho scritto prima, e g(x) il numeratore”.
“Che roba. Ehi, però c'è un'esponenziale con esponente −x, come mai?”.
“L'abbiamo fatto solo per comodità, invece di avere l'esponenziale con esponente x che moltiplica g, abbiamo diviso tutto per ex per ottenere quell'integrale, che ci piace molto perché ha un fattoriale al denominatore. E quando nei denominatori ci sono di mezzo i fattoriali sappiamo che tutto diventa piccolo molto in fretta”.
“Già, il fattoriale diventa enorme molto in fretta”.
“E allora, se immaginiamo che π possa essere una frazione N/D, moltiplicandolo per D dovremmo ottenere un intero, e quindi anche l'espressione f(iDπ) − eiDπg(iDπ) sarà un intero, perché la formula più bella della matematica ci dice che eiπ è uguale a 1, mentre f(x) e g(x) sono polinomi”.
“Siii, e quindi?”.
“E quindi avremmo un intero positivo minore di un numero piccolo quanto vogliamo. Minore di 1, ad esempio”.
“Ma non esistono interi positivi minori di 1, no?”.
“Appunto: è assurdo. Quindi π non può essere una frazione”.
“Ah! Ecco la dimostrazione!”.
“Noi però vogliamo dimostrare che π è trascendente, non ci basta che sia irrazionale”.
“Oh, no, è vero! Per un attimo avevo avuto l'illusione di aver finito”.
“Eh, no. Questo era solo riscaldamento. La strada per dimostrare che π è trascendente segue, però, quella che abbiamo percorso adesso, con ulteriori complicazioni”.
“Capirai”.
“Per prima cosa, si prendono in considerazioni delle approssimazioni di Padé simultanee”.
“Ossignore”.
“Significa semplicemente che approssimano bene non solo in un punto, ma in tanti punti. In quell'integrale che ho scritto sopra, invece di avere una sola parentesi del tipo (t − x) ce ne saranno tante diverse”.
“Mah”.
“Avremo quindi polinomi f e g che non dipendono solo da una x, ma da tante x diverse”.
“Cioè avremo x1, x2, e così via?”.
“Esatto”.
“Ma tutto questo perché?”.
“Eh, prima non ne abbiamo avuto bisogno perché abbiamo supposto che π fosse una frazione, e ci è bastata una approssimazione di Padé normale”.
“Normale”.
“Ora, invece, se vogliamo dimostrare che π è trascendente, l'assurdo dovrebbe partire dalla supposizione che π sia algebrico. E non tutti i numeri algebrici sono frazioni”.
“E allora come si fa?”.
“Se quei numeri algebrici li moltiplichiamo per opportuni altri numeri algebrici, però, diventano frazioni”.
“Uh, ma come? Fammi capire”.
“Prendi per esempio la radice di 2”.
“Ok”.
“Se la moltiplichi per radice di 2, ottieni 2, che è addirittura naturale”.
“Vabbé, così è facile”.
“Prendi allora l'espressione (3 − √2)”.
“Ok”.
“Se la moltiplichi per (3 + √2) ottieni 9 − 2 = 7”.
“Ah, vero. Funziona sempre questa cosa?”.
“Sì, per ogni numero algebrico esistono sempre altri numeri algebrici che, moltiplicati per il primo, mi danno un numero razionale. È legato al fatto che i numeri algebrici sono sempre soluzioni di polinomi con coefficienti interi: quindi dato il numero iniziale, prendo il polinomio di grado minimo di cui questo è soluzione. Questo avrà un certo numero di altre radici, e se le moltiplico tutte ottengo il termine noto di quel polinomio, che è un numero intero”.
“Forse ho capito, posso provare un esempio?”.
“Certo!”.
“Se prendo la radice cubica di 3, so che questa è soluzione di x3 − 3=0”.
“Giusto”.
“Quindi se prendo le tre soluzioni dell'equazione x3 − 3 = 0, e le moltiplico tra loro… cosa ottengo?”.
“Pensaci bene: se le tre soluzioni sono x1, x2 e x3, l'equazione x3 − 3 = 0 può anche essere scritta come (x − x1)(x − x2)(x − x3) = 0”.
“Vero”.
“E allora se svolgi tutto dove va a finire il prodotto x1x2x3?”.
“Ah! Nel termine noto, che è 3! Molto bene, funziona davvero”.
“E funziona anche con la somma: quanto fa x1 + x2 + x3?”.
“Vediamo, devo sempre prendere in considerazione quel prodotto di tre parentesi?”.
“Sì: dove salta fuori la somma delle tre soluzioni?”.
“Mi pare che si possa trovare nel coefficiente del termine di secondo grado: quando faccio tutti i possibili prodotti, posso raccogliere x2 e ottenere, come coefficiente, la somma x1 + x2 + x3”.
“Per essere più precisi, la somma cambiata di segno, ma non è molto importante. Il fatto importante è che la somma sia il coefficiente del termine di secondo grado, quindi ancora una volta un numero intero”.
“Ah, bene”.
“Dato che questi numeri che servono per avere somma e prodotto interi sono molto importanti in questo campo, i Veri Matematici hanno creato una definizione apposta per loro: si chiamano coniugati della radice del polinomio che abbiamo preso in considerazione”.
“Ok”.
“Ecco allora come funziona il giochino delle approssimazioni di Padé: vogliamo dimostrare che ea non può essere uguale a −1, qualunque sia a, algebrico. Si prendono allora tutti i coniugati di a, e si considerano i prodotti aventi come fattori (eai + 1), in cui i termini ai sono, appunti, i coniugati”.
“Le cose si complicano”.
“Già. Poi si considerano le approssimazioni di Padé simultanee, cioè quelle approssimazioni che approssimano bene tutti i termini del tipo eb che saltano fuori svolgendo i prodotti appena fatti”.
“Oh, mamma”.
“Ancora una volta salta fuori un integrale con un bel fattoriale al denominatore”.
“E i fattoriali ci piacciono”.
“Esatto. Così risulta un numero naturale che può essere minore di 1”.
“E questo è impossibile”.
“Purché non sia zero…”.
“Santo cielo! Ma non c'è mai fine!”.
“La dimostrazione del fatto che quel numero che salta fuori non è zero ha bisogno delle congruenze, ma non mi azzardo a scrivere tutti i passaggi: ti dico solo che si riesce a vedere che comunque noi scegliamo un numero primo p quel numero è congruente a una certa espressione positiva modulo p. Se quindi prendiamo un numero primo p abbastanza grande, quel numero è positivo”.
“E dato che i numeri primi sono infiniti…”.
“Un numero primo abbastanza grande lo troviamo sempre, e qui la dimostrazione finisce davvero”.
“Gulp. Comincio a capire perché è una dimostrazione del 1882”.
“Eh, sì. Sviluppi in serie, formula di Eulero, integrali, approssimazioni, infinità dei numeri primi: contiene di tutto.”.
“Che fatica! Non oso pensare alla fatica che hanno fatto quelli che sono arrivati alla dimostrazione per primi”.
“Eh, erano bravi”.
“Oh, bene”.
“Facciamo un riassunto di tutto quello che abbiamo detto finora”.
“Ottimo”.
“I numeri reali si dividono in due categorie: i numeri razionali, cioè le frazioni, e i numeri irrazionali”.
“Cioè tutti gli altri”.
“Esatto. Ora, anche gli irrazionali sono divisibili in due categorie: i numeri algebrici (di cui fanno parte anche i razionali) e i numeri trascendenti”.
“I numeri algebrici sono quelli che possono essere soluzioni di equazioni polinomiali, vero?”.
“Equazioni polinomiali a coefficienti interi, altrimenti tutti i numeri potrebbero essere soluzioni dell'equazione x = a, e fine della storia”.
“Giusto”.
“Invece i trascendenti non possono essere soluzioni di equazioni polinomiali a coefficienti interi”.
“E fin qua ci siamo”.
“Alcuni numeri algebrici, poi, sono costruibili”.
“Il che significa che sono costruibili con riga e compasso, vero?”.
“Sì. Con riga e compasso si possono costruire numeri che, a partire dall'unità, possono essere ottenuti con un numero finito di somme, sottrazioni, moltiplicazioni, divisioni, e estrazioni di radice quadrata”.
“E ora c'è pi greco”.
“Già. Il problema della quadratura del cerchio si traduce in questa domanda: usando solo riga e compasso è possibile costruire un quadrato avente la stessa area di un cerchio dato? Domanda che, in linguaggio aritmetico, diventa: pi greco è un numero costruibile?”.
“E la risposta è no”.
“La risposta è: pi greco è un numero trascendente, e quindi se non appartiene all'insieme dei numeri algebrici non può appartenere nemmeno all'insieme dei numeri costruibili, che è un sottoinsieme proprio degli algebrici. Ma la dimostrazione di questa affermazione è lunga e difficile”.
“Lo sospettavo”.
“Ricordi quando abbiamo dimostrato l'esistenza di un numero trascendente?”.
“Sì, abbiamo usato una proprietà dei trascendenti, se ben ricordo, che riguardava le approssimazioni che possiamo fare con le frazioni”.
“Esatto: il numero che abbiamo trovato può essere approssimato con frazioni del tipo m/n con precisione minore di 1/nk, per qualunque k”.
“Anche pi greco, quindi?”.
“Purtroppo no, per pi greco questo metodo non funziona. Bisogna generalizzarlo tanto”.
“Questo tanto mi inquieta”.
“Cominciamo con notare che π ed e, il numero di Nepero, sono strettamente legati”.
“Non sarà la solita storia della formula più bella della matematica?”.
“Eh, sì. Sappiamo che eiπ = −1”.
“Ok, e quindi?”.
“E quindi se riusciamo a dimostrare che ea, con a un qualunque numero algebrico, non può essere uguale a −1, siamo a posto”.
“Fammi capire”.
“Dato che sappiamo che eiπ è effettivamente uguale a −1, se riusciamo a dimostrare quel teorema possiamo concludere che iπ non è algebrico”.
“Quindi iπ è trascendente, ma come facciamo a togliere i?”.
“Beh, è facile, i è algebrico, perché è soluzione dell'equazione a coefficienti interi x2 + 1=0, e quindi se il prodotto iπ è trascendente, significa che π deve esserlo”.
“Ah, ecco! Ottimo, quindi in effetti abbiamo spostato il problema dallo studio di pi greco allo studio della funzione esponenziale, vero?”.
“Proprio così. Ora, facciamo un passo più semplice di quello che vorremmo, giusto per capire come funzionano le cose: dimostriamo che e è irrazionale. Ci ricordiamo che per la funzione esponenziale esiste una serie di potenze che converge a essa”.
“Ed ecco che entra in campo l'analisi…”.
“Sì, una dimostrazione di teoria dei numeri fatta con l'analisi: bella roba. Ricordi quale serie di potenze converge all'esponenziale?”.
“Era una serie facile, mi pare 1 + x + x2/2! + x3/3! + …”.
“Esatto. Ora, supponiamo per assurdo che e sia razionale, cioè una frazione. Questo vuol dire che se moltiplico questa fantomatica frazione per un numero sufficientemente grande, ottengo un numero intero”.
“Certamente”.
“Allora calcolo n!e1, con n sufficientemente grande da fare in modo che il denominatore se ne vada. E uso proprio lo sviluppo in serie di ex”.
“Va bene, aspetta che provo a capire. Se prendo la serie dell'esponenziale vedo che si semplificano tanti denominatori”.
“Quanti?”.
“Beh, sicuramente quelli fino a xn/n!”.
“Giusto; e ricorda che abbiamo posto x = 1. Che succede dopo quel termine?”.
“Eh, mi sa che rimane una frazione: 1/(n + 1). Anzi, non solo una, poi c'è 1/(n + 1)(n + 2), e così via”.
“Esatto. E quindi n!e non può essere un intero”.
“E quindi e non può essere razionale! Molto bello”.
“E ora un altro passo di analisi: quello che abbiamo dimostrato non è che esiste soltanto un caso in cui, moltiplicando la frazione che dovrebbe essere uguale a e, si ottiene un assurdo. Di casi come quello che ne sono infiniti, basta prendere il moltiplicatore sempre più grande”.
“D'accordo”.
“Ogni volta che moltiplichiamo l'espansione in serie di e otteniamo una prima parte intera, e poi una coda composta da tante frazioni aventi il numeratore uguale a 1, e il denominatore che diventa sempre più grande.”.
“Immagino che il passo di analisi sia fare diventare infinitamente grande quel denominatore”.
“Immagini bene. Quello che abbiamo fatto, detto in altri termini, è questo: abbiamo trovato due successioni fn e gn tali che la differenza fne − gn diventa sempre più piccola man mano che n diventa sempre più grande. Nel nostro caso, giusto per essere chiari, fn è uguale a n!, mentre gn è uguale a 1/(n + 1) + 1/(n + 1)(n + 2) + …”.
“Ok, ho capito”.
“Quindi questa è una tecnica per dimostrare che un numero è irrazionale: trovo due successioni con quelle proprietà, e sono a posto”.
“Bene”.
“Ora un altro passo: passiamo dalla dimostrazione di irrazionalità di e1 alla dimostrazione di irrazionalità di ea, con a razionale diverso da zero”.
“Procediamo sempre allo stesso modo, con quelle due successioni?”.
“Sì, ma ora dobbiamo farlo per il caso generale, dove l'esponente di e è variabile. E l'aiuto ci viene proprio dalle approssimazioni di Padé”.
“Oh”.
“Sì, dal fatto che ex può essere approssimata molto bene dal rapporto f(x)/g(x), eliminando il denominatore possiamo passare all'espressione g(x)ex − f(x), che diventa sempre più piccola all'aumentare del numero di termini con cui faccio l'approssimazione”.
“Mamma mia”.
“Uno studio super tecnico di come sono fatti i polinomi f(x) e g(x) porta alla dimostrazione dell'ultima affermazione”.
“Super tecnico?”.
“Sì, vengono espressi come funzioni integrali di altre funzioni, in modo da poter costruire delle disuguaglianze comode e utili”.
“Certo, comode e utili…”.
“L'analisi è la matematica delle disuguaglianze: tutto è stima”.
“Andiamo bene”.
“Ti faccio solo un esempio, giusto per darti un'idea del livello: l'approssimazione di Padé di ordine 8 per la funzione esponenziale è questa: ”.
(x8 − 72x7 + 2520x6 − 55440x5 + 831600x4 − 8648640x3 + 60540480x2 − 259459200x + 518918400) / (x8 + 72x7 + 2520x6 + 55440x5 + 831600x4 + 8648640x3 + 60540480x2 + 259459200x + 518918400)
“Argh”.
“Che corrisponde a questa bella formuletta:”.
“Orrore”.
“Dove f(x) è il denominatore della frazione enorme che ho scritto prima, e g(x) il numeratore”.
“Che roba. Ehi, però c'è un'esponenziale con esponente −x, come mai?”.
“L'abbiamo fatto solo per comodità, invece di avere l'esponenziale con esponente x che moltiplica g, abbiamo diviso tutto per ex per ottenere quell'integrale, che ci piace molto perché ha un fattoriale al denominatore. E quando nei denominatori ci sono di mezzo i fattoriali sappiamo che tutto diventa piccolo molto in fretta”.
“Già, il fattoriale diventa enorme molto in fretta”.
“E allora, se immaginiamo che π possa essere una frazione N/D, moltiplicandolo per D dovremmo ottenere un intero, e quindi anche l'espressione f(iDπ) − eiDπg(iDπ) sarà un intero, perché la formula più bella della matematica ci dice che eiπ è uguale a 1, mentre f(x) e g(x) sono polinomi”.
“Siii, e quindi?”.
“E quindi avremmo un intero positivo minore di un numero piccolo quanto vogliamo. Minore di 1, ad esempio”.
“Ma non esistono interi positivi minori di 1, no?”.
“Appunto: è assurdo. Quindi π non può essere una frazione”.
“Ah! Ecco la dimostrazione!”.
“Noi però vogliamo dimostrare che π è trascendente, non ci basta che sia irrazionale”.
“Oh, no, è vero! Per un attimo avevo avuto l'illusione di aver finito”.
“Eh, no. Questo era solo riscaldamento. La strada per dimostrare che π è trascendente segue, però, quella che abbiamo percorso adesso, con ulteriori complicazioni”.
“Capirai”.
“Per prima cosa, si prendono in considerazioni delle approssimazioni di Padé simultanee”.
“Ossignore”.
“Significa semplicemente che approssimano bene non solo in un punto, ma in tanti punti. In quell'integrale che ho scritto sopra, invece di avere una sola parentesi del tipo (t − x) ce ne saranno tante diverse”.
“Mah”.
“Avremo quindi polinomi f e g che non dipendono solo da una x, ma da tante x diverse”.
“Cioè avremo x1, x2, e così via?”.
“Esatto”.
“Ma tutto questo perché?”.
“Eh, prima non ne abbiamo avuto bisogno perché abbiamo supposto che π fosse una frazione, e ci è bastata una approssimazione di Padé normale”.
“Normale”.
“Ora, invece, se vogliamo dimostrare che π è trascendente, l'assurdo dovrebbe partire dalla supposizione che π sia algebrico. E non tutti i numeri algebrici sono frazioni”.
“E allora come si fa?”.
“Se quei numeri algebrici li moltiplichiamo per opportuni altri numeri algebrici, però, diventano frazioni”.
“Uh, ma come? Fammi capire”.
“Prendi per esempio la radice di 2”.
“Ok”.
“Se la moltiplichi per radice di 2, ottieni 2, che è addirittura naturale”.
“Vabbé, così è facile”.
“Prendi allora l'espressione (3 − √2)”.
“Ok”.
“Se la moltiplichi per (3 + √2) ottieni 9 − 2 = 7”.
“Ah, vero. Funziona sempre questa cosa?”.
“Sì, per ogni numero algebrico esistono sempre altri numeri algebrici che, moltiplicati per il primo, mi danno un numero razionale. È legato al fatto che i numeri algebrici sono sempre soluzioni di polinomi con coefficienti interi: quindi dato il numero iniziale, prendo il polinomio di grado minimo di cui questo è soluzione. Questo avrà un certo numero di altre radici, e se le moltiplico tutte ottengo il termine noto di quel polinomio, che è un numero intero”.
“Forse ho capito, posso provare un esempio?”.
“Certo!”.
“Se prendo la radice cubica di 3, so che questa è soluzione di x3 − 3=0”.
“Giusto”.
“Quindi se prendo le tre soluzioni dell'equazione x3 − 3 = 0, e le moltiplico tra loro… cosa ottengo?”.
“Pensaci bene: se le tre soluzioni sono x1, x2 e x3, l'equazione x3 − 3 = 0 può anche essere scritta come (x − x1)(x − x2)(x − x3) = 0”.
“Vero”.
“E allora se svolgi tutto dove va a finire il prodotto x1x2x3?”.
“Ah! Nel termine noto, che è 3! Molto bene, funziona davvero”.
“E funziona anche con la somma: quanto fa x1 + x2 + x3?”.
“Vediamo, devo sempre prendere in considerazione quel prodotto di tre parentesi?”.
“Sì: dove salta fuori la somma delle tre soluzioni?”.
“Mi pare che si possa trovare nel coefficiente del termine di secondo grado: quando faccio tutti i possibili prodotti, posso raccogliere x2 e ottenere, come coefficiente, la somma x1 + x2 + x3”.
“Per essere più precisi, la somma cambiata di segno, ma non è molto importante. Il fatto importante è che la somma sia il coefficiente del termine di secondo grado, quindi ancora una volta un numero intero”.
“Ah, bene”.
“Dato che questi numeri che servono per avere somma e prodotto interi sono molto importanti in questo campo, i Veri Matematici hanno creato una definizione apposta per loro: si chiamano coniugati della radice del polinomio che abbiamo preso in considerazione”.
“Ok”.
“Ecco allora come funziona il giochino delle approssimazioni di Padé: vogliamo dimostrare che ea non può essere uguale a −1, qualunque sia a, algebrico. Si prendono allora tutti i coniugati di a, e si considerano i prodotti aventi come fattori (eai + 1), in cui i termini ai sono, appunti, i coniugati”.
“Le cose si complicano”.
“Già. Poi si considerano le approssimazioni di Padé simultanee, cioè quelle approssimazioni che approssimano bene tutti i termini del tipo eb che saltano fuori svolgendo i prodotti appena fatti”.
“Oh, mamma”.
“Ancora una volta salta fuori un integrale con un bel fattoriale al denominatore”.
“E i fattoriali ci piacciono”.
“Esatto. Così risulta un numero naturale che può essere minore di 1”.
“E questo è impossibile”.
“Purché non sia zero…”.
“Santo cielo! Ma non c'è mai fine!”.
“La dimostrazione del fatto che quel numero che salta fuori non è zero ha bisogno delle congruenze, ma non mi azzardo a scrivere tutti i passaggi: ti dico solo che si riesce a vedere che comunque noi scegliamo un numero primo p quel numero è congruente a una certa espressione positiva modulo p. Se quindi prendiamo un numero primo p abbastanza grande, quel numero è positivo”.
“E dato che i numeri primi sono infiniti…”.
“Un numero primo abbastanza grande lo troviamo sempre, e qui la dimostrazione finisce davvero”.
“Gulp. Comincio a capire perché è una dimostrazione del 1882”.
“Eh, sì. Sviluppi in serie, formula di Eulero, integrali, approssimazioni, infinità dei numeri primi: contiene di tutto.”.
“Che fatica! Non oso pensare alla fatica che hanno fatto quelli che sono arrivati alla dimostrazione per primi”.
“Eh, erano bravi”.
Iscriviti a:
Commenti (Atom)