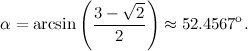Una costante universale

In questo periodo natalizio di scambio di regali, mi torna alla mente un vecchio quesito di Rudi Mathematici.

Prendete due pezzi di Lego del tipo 1×x (con x maggiore di 1), attaccateli in modo che abbiano un solo attacco in comune, e fateli ruotare in modo da ottenere un angolo acuto che sia il più piccolo possibile.

Bene: quanto misura questo angolo?

Il testo è tutto qui, non ci sono altri dati; per essere più precisi, non è necessario cercare altri dati, la risposta è unica, purché si tenga conto di un dettaglio costruttivo (facilmente verificabile andando a recuperare due mattoncini dei Lego): l'incastro a forma di cilindretto utilizzato per attaccare i pezzi uno sopra l'altro ha il raggio più grande possibile. Un pezzo di Lego “da uno”, una volta incastrato su un qualunque altro pezzo, può ruotare su sé stesso liberamente, sfiorando i cilindretti che gli stanno intorno.

Mi sono divertito a costruire la figura di due pezzi 1×2 incastrati uno sull'altro e ruotati come richiesto dal quesito. Il fatto notevole è che questa costruzione può essere effettuata con riga e compasso, senza numeri.

Eccola qua:

A suo tempo feci il calcolo dell'ampiezza dell'angolo. Il risultato è:

E questa è, senza dubbio, una costante universale.

People hearing without listening

(continua da qui)

4. Venne un altro ministro, che modificò radicalmente il quadro orario delle superiori. Tolse tante sperimentazioni, e ridusse il numero di ore di lezione durante la settimana. Per quanto riguarda matematica, ci disse che in terza le ore sarebbero passate da 4 a 3, ma poi si sarebbe aggiunta una nuova materia, denominata complementi di matematica, per un'ora in più alla settimana. Da 4 saremmo gattopardescamente passati a 3+1.

Diamo un'occhiata ai programmi, ci siamo detti noi docenti, per capire un po' cosa sarebbe cambiato. Non sto qui a farvi vedere lo schema della suddivisione degli argomenti, ma vi farò solo un esempio riguardante uno specifico argomento.

Matematica: funzioni logaritmiche.
Complementi di matematica: il logaritmo in base e.

[Per i non addetti ai lavori: sarebbe come scrivere, in un programma di grammatica, la voce "articoli determinativi", e in un ipotetico programma di complementi di grammatica, la voce "l'articolo lo"]


5. Nel mondo della scuola 3+1 non fa 4, sarebbe troppo facile. Una materia in più significa tante cose, tutte quante aventi a che fare con la burocrazia. Per questo motivo (e per altri problemi analoghi in altre materie) invitammo a scuola un super esperto, uno di quelli che erano nella commissione riforma e avevano pensato, nel dettaglio, a queste modifiche. Quella che segue è una trascrizione il più possibile fedele della nostra richiesta di chiarimenti.

«Abbiamo un problemino».

«Dite pure».

«Con questa nuova materia, complementi di matematica, come dobbiamo comportarci? Abbiamo due voti? Perché se una insufficienza in matematica è un problema, due sono ancora peggio».

«Ma no, ma non importa, ma figuriamoci. Lo scopo non era questo, si voleva introdurre una materia che mostrasse l'applicazione della matematica nella tecnica [il lettore non dimentichi il logaritmo in base e citato poco fa]».

«No, va bene, certo, ma in pagella quindi come facciamo?».

«Guardate, voi dite all'ufficio scolastico regionale che mettete un voto unico [i capelli della preside si rizzano come se qualcuno le avesse collegato un generatore di Van der Graaf alle orecchie]».

«Ma possiamo?».

«Voi dite così, e se loro hanno delle idee migliori ve le fate raccontare».

«Ehm, ok. Ma se ci fossero due insegnanti?».

«In che senso?».

«Eh, nel senso che potremmo avere un insegnante che insegna matematica e uno che insegna complementi, ha presente la faccenda delle 18 ore?».

«Ah, non ci avevo pensato [rileggete pure quanto volete, questa è una citazione esatta]».

«Perché con due insegnanti non si può mica mettere un voto unico».

«Eh, no».

«E quindi?».

«Guardate, devo dire che, quando in commissione si decise per inserire i complementi di matematica, io ero assente [giuro, ha detto così, davvero]. Ma mi informerò e vi saprò dire».


5. Non ci seppe mai dire nulla, ma ci pensò il ministero in persona, con due comunicazioni. Fino all'anno scorso, per molte materie comparivano due voti nella pagella del primo quadrimestre: uno voto per lo scritto e uno per l'orale.

A inizio anno scolastico il ministero ci disse che, nelle classi interessate dalla riforma, non avremmo più dovuto mettere due voti in pagella, ma uno solo. Va bene, quindi avremmo avuto un voto per matematica e uno per complementi.

Poi, i primi di dicembre [dicembre, non settembre], ci disse che il voto di complementi si sarebbe dovuto fondere con quello di matematica. Quindi un solo voto, anche se ci sono due insegnanti diversi.

Se non vi è chiara l'implicazione, immaginate per un momento di tornare a scuola e di avere un insegnante di matematica che non vi dà il voto. Ecco.

Hello darkness, my old friend

Questa storia, che riguarda la scuola italiana, è suddivisa in varie parti che ripercorrono i contributi dati dai vari ministri allo scopo di renderla… bé, giudicate voi e completate la frase a vostro piacimento.


1. C'era una volta, ai tempi in cui io ero studente, il concetto di continuità didattica. Secondo tale ispirato principio, un insegnante avrebbe dovuto mantenere, in anni successivi, le classi avute in precedenza, fino al completamento del ciclo scolastico. Tradotto in parole povere: chi si prende la seconda, quest'anno? Chi ha insegnato in prima l'anno scorso, perché conosce gli studenti, può proseguire il programma, non deve ricominciare, e così via.

(per chi ha fretta e ha capito: potete saltare al punto 2)

Nella scuola in cui insegno le cattedre erano organizzate, quindi, nel modo seguente. In prima c'erano 5 ore di matematica, e così anche in seconda, in terza ce n'erano 4, in quarta 3 e in quinta ancora 3. Un insegnante si poteva prendere, per esempio, una prima, una seconda, una terza e una quarta (5+5+4+3=17), l'anno dopo una nuova prima, la seconda che aveva l'anno precedente quando era una prima, la quarta — che era la terza — e la quinta — che era la quarta — (5+5+3+3=16).

L'anno successivo quell'insegnante avrebbe avuto la prima, la seconda, la terza e la quinta (5+5+4+3=17), e poi il ciclo sarebbe ricominciato, mantenendo sempre la continuità didattica. Non ho specificato che, nella mia scuola, la terza è una classe nuova: dopo il biennio gli studenti vengono smistati nelle terze di indirizzo, quindi non si ha continuità sulla terza.


2. Come la mettiamo col fatto che gli insegnanti devono fare 18 ore di lezione? Negli esempi qui sopra questo non succede mai, si arriva a 17 o addirittura a 16 ore: e le altre? Bé, ai tempi esisteva un altro concetto importante: quello di ore a disposizione. Nell'orario dell'insegnante erano inserite alcune ore (dette, appunto, ore a disposizione) in cui si doveva essere a scuola, disponibili a sostituire colleghi assenti, oppure a fare assistenza agli alunni che non volevano avvalersi dell'insegnamento della religione. Poteva capitare, ogni tanto, di non avere lezione in una di quelle ore: bisognava comunque essere a scuola disponibili, in caso di imprevisti.


3. Venne un ministro che stabilì che le ore a disposizione dovessero essere abolite. Gli orari dovevano essere composti da 18 ore effettive di lezione. Come si poteva fare, nella nostra scuola? Gli insegnanti più anziani (quelli più avanti nella graduatoria, quelli che "scelgono per primi") potevano cavarsela con un (5+5+5+3), ma con qualche problema: non ci sarebbero state abbastanza classi da 5 ore per tutti. Qualcuno si sarebbe preso una 4+4+4+3+3, ad esempio (una classe in più significa più consigli, più compiti, più ricevimenti, ma pazienza: chi viene dopo in graduatoria è giovane e si arrangia, quando sarà vecchio e non ce la farà più potrà avere una classe in meno); ma il problema più grosso è che molte continuità didattiche sarebbero saltate. Gli studenti di terza non avrebbero avuto lo stesso insegnante in quarta e in quinta, ad esempio.

Con questo sistema il ministro ottenne un risparmio di denaro: le ore a disposizione non esistevano più e, quindi, non erano da pagare. Il rendimento di qualche insegnante, però, subì un certo calo: come pensate che sia insegnare gli stessi argomenti a sei classi uguali (6×3=18 — caro insegnante, quest'anno hai sei quinte, spieghi le stesse cose e poi le porti anche all'esame)?

E come si fa con le supplenze? Bé, qualche ora a disposizione rimane comunque: a volte i conti non tornano e rimane qualche cattedra a meno di 18 ore, e se non ci sono abbastanza insegnanti, bé, convinciamo gli studenti che non fanno religione a uscire dalla scuola, o mettiamoli tutti in un'aula senza nessuno che li controlli (come? attività alternative? non scherziamo, dai). E se non si riesce a sostituire l'insegnante ammalato, via, distribuiamo gli studenti nelle altre classi (come? più di 30 studenti in un'aula? in due in un banco? e la sicurezza? le norme? non scherziamo, dai). Se proprio è necessario, la scuola paghi pure qualche insegnante per le ore critiche (le prime, ad esempio), l'importante è che non le paghi il ministero.

Fino all'anno scorso le cose stavano così. Poi, per quanto riguarda matematica, c'è stata una novità. Visto che questo post è già esageratamente lungo, la racconto nel prossimo.

Devo migliorare il mio vocabolario

Il biglietto di auguri di quelli di seconda conteneva questo:

Ma perché proprio le frequenze? — come funzionano gli mp3

La domanda era: abbiamo davvero bisogno di tutte quelle frequenze? Cioè, ok, un suono bello, ricco, piacevole da ascoltare, è composto da tante onde “pure”, ognuna delle quali dà un piccolo contributo al risultato finale. Ma davvero il nostro orecchio riesce a percepirle tutte?

Qui si entra nel mondo della psicoacustica, che sarebbe (scopiazzando la definizione da wikipedia) lo studio della psicologia della percezione acustica. Insomma: cosa è per noi la musica? Cosa sentiamo davvero? I suoni esistono solo se li ascoltiamo? Se un albero cade in una foresta e nessuno assiste alla scena, la vecchina del piano di sotto verrà ugualmente a brontolare perché non si possono spostare i mobili a mezzanotte?

Bene, la filosofia della compressione mp3 (e di tutta la categoria di algoritmi di compressione detti a perdita di informazione) è questa: se una cosa non si sente, non esiste. Se quella frequenza non è percepibile dall'orecchio, allora la sua presenza è inutile: buttiamola via. Se devo registrare lo sparo di un cannone, è inutile che memorizzi anche il suono della mosca che volava lì vicino.

A grandi linee (molto grandi), un codificatore mp3 fa questo: prende in ingresso l'onda, la trasforma nell'elenco delle frequenze componenti, butta via le frequenze inutili, e produce un file decisamente più piccolo rispetto all'originale.

Anche se il file risultante è diverso dall'originale, l'orecchio umano non se ne accorge. O, almeno, non dovrebbe. Certamente non se ne accorgono i giovani d'oggi che ascoltano la musica in coppia, dividendosi le cuffie da buoni amici, un auricolare per uno (signora mia, dove andremo a finire? Nemmeno conoscono il concetto di stereofonia). Più difficile è affermare che nessuno se ne accorge: personalmente ho fatto una prova con un amico che possiede un impianto audio che costa di più della mia automobile, gli ho dato un cd contenente alcuni brani registrati sia in formato originale, sia passati attraverso la codifica/decodifica mp3, e lui ha saputo distinguerli.

Ecco, comunque, una prova oggettiva: ho preso il file contenente il la a 220 Hz suonato da una chitarra, file che avevo già usato nel post precedente, e l'ho compresso in formato mp3. Poi ho disegnato lo spettro. Eccoli qua, quello originale e quello dopo la compressione:

Si vede bene che nella parte sinistra sembrano uguali, ma poi nella parte destra cambiano notevolmente. Il file mp3, ad esempio, non contiene informazioni per le frequenze superiori ai 16000 Hz (tanto chi le sente?).

Credo che ci sia una morale, in questa faccenda dell'evoluzione del modo in cui viene memorizzata la musica.  Da ragazzini, i miei amici ed io sapevamo cosa fosse una puntina di un giradischi, qualcuno sapeva anche distinguere tra magnete mobile e bobina mobile, andavamo nei negozi ad ammirare oggetti per noi proibiti, robe con nomi esotici come amplificatori valvolari in classe A, bracci tangenziali, diffusori elettrostatici, preamplificatori phono. E, quando ascoltavamo della musica, al massimo ogni venti minuti dovevamo alzarci per girare il disco.

Cercavamo la migliore fedeltà possibile e, adesso che abbiamo una tecnologia che ci permetterebbe di portarci una sala da concerto in casa, ci accontentiamo di poche frequenze trasmesse da un auricolare in un orecchio (bah, forse la morale è che sto invecchiando).

Se una farfalla batte le ali a Pechino, a New York nessuno la sente.

Ma perché proprio le frequenze? — spettri

Quindi i suoni cominciano a diventare interessanti quando non sono composti da un'unica onda sinusoidale. E non devono nemmeno essere composti da più onde sinusoidali aventi la stessa frequenza, perché la somma di tante onde di quel tipo produce, alla fine, sempre un'unica sinusoide.

Dunque servono tante frequenze diverse.

Le onde sinusoidali sono gli atomi che compongono l'universo delle onde, gli elementi base a partire dai quali si può fare tutto.

Siamo anche in grado di smontare un'onda complessa, in modo da capire come sono fatti i suoi atomi: possiamo capire quali sono le frequenze che la compongono. Per farlo, si utilizza l'analisi di Fourier, che ci permette di visualizzare in un grafico tutte le componenti sinusoidali.

Per avere un'idea, prendiamo il la dell'ottava centrale del pianoforte, la nota usata come riferimento ufficiale per accordare tutti gli strumenti. Nella sua forma più semplice, è una sinusoide che oscilla 440 volte al secondo. Il grafico di cui parlavo prima (che si chiama spettro delle frequenze) è fatto così:

In un mondo perfetto si dovrebbe vedere un unico segmento verticale in corrispondenza della frequenza di 440 Hz, qui si vede un picco in corrispondenza di quella frequenza e un po' di rumore di fondo. La scala verticale è logaritmica,quindi il rumore è davvero molto in basso, ed è dovuto anche alle approssimazioni fatte dal computer per memorizzare un'onda attraverso i punti di cui è costituita.

Lo spettro di un'onda sinusoidale è quindi il più semplice possibile: una righina che corrisponde alla frequenza dell'onda.

Questo invece è lo spettro di un'onda composta da due sinusoidi aventi frequenze diverse (insomma: due note diverse):

Oltre alla nota precedente, il la a 440 Hz, qui ho aggiunto il la dell'ottava superiore, a 880 Hz: si vedono chiaramente due picchi, corrispondenti alle due diverse frequenze.

E adesso prendiamo una nota vera: ho registrato da un pianoforte elettrico il solito la (il fatto che la nota sia stata generata elettronicamente e non da una corda che vibra fa sì che non si possa proprio dire che la nota è vera, però ci assomiglia… insomma, non è così sgradevole come una sinusoide). Ecco la forma d'onda:

Si vede che è periodica, ma certamente non è una sinusoide (assomiglia di più a un'onda quadra, segno della sua natura elettronica). Ed ecco lo spettro:

Un sacco di frequenze: tutte, in misura più o meno evidente, contribuiscono alla creazione del suono finale. La nota è sempre la stessa, ma il timbro, cioè la sensazione che proviamo ascoltandola, ciò che ci fa riconoscere il suono tipico del pianoforte, è diverso. È questa ricchezza di frequenze superflue (ehm) che ci fa apprezzare i suoni (ed è per questo che dico ai miei studenti che la roba che ascoltano in discoteca non si può chiamare musica, ma non divaghiamo).

Infine, un'ultima onda vera, il la di una chitarra. Io pensavo che fosse anche quello a 440 Hz, ma non è così. Lo spettro mi ha rivelato (e l'internet ha confermato) che la corda la di una chitarra suona a 110 Hz, due ottave sotto rispetto a quello che pensavo. Siccome 110 Hz è molto vicino al limite sinistro del grafico, ho pensato che fosse meglio far vedere il la dell'ottava successiva, quello che si ottiene facendo suonare solo mezza corda.

Ecco l'onda:

e lo spettro:

E ora la domanda: abbiamo davvero bisogno di tutte quelle frequenze?

Ma perché proprio le frequenze? — somme di sinusoidi

E allora, come si generano suoni diversi? E note diverse?

Facciamo un passo alla volta, vediamo che succede sommando due sinusoidi. Si possono fare i passaggi algebrici (noiosi) per scoprire il risultato, ma è molto più facile vedere un disegno. Abbiamo visto che un'onda può essere generata a partire da un punto che ruota su una circonferenza: generalizziamo un po'. Invece di pensare a un punto rotante, pensiamo a un vettore che ruota (semplicemente colleghiamo con una freccia il centro della circonferenza col punto che gira).

Ora, che succede se modifichiamo la lunghezza del vettore? Stiamo modificando l'ampiezza dell'onda. Il regolatore di volume è il regolatore della lunghezza del vettore.

E se di vettori ne abbiamo due? Ecco qua quello che succede, giocateci un po': sono disponibili i comandi per regolare le lunghezze dei due vettori e l'angolo tra di loro (cioè la famosa fase). Il risultato è evidente, la somma di due vettori è facile da disegnare:

Questa è un'Applet Java creata con GeoGebra da www.geogebra.org - Java non risulta installato sul computer in uso - fare riferimento a www.java.com (esce un po' dal margine, ma se lo rimpicciolisco ancora non si vede più niente)

La somma di due sinusoidi aventi la stessa frequenza è ancora una sinusoide avente la stessa frequenza (magari il volume finale sarà diverso, e così anche la fase).

Quindi, se sommo due note uguali ottengo sempre la stessa nota.

E, dunque, se voglio note diverse devo avere frequenze diverse. Con una sola frequenza non posso fare musica.

Ecco qua un disegno che rappresenta, in grigio, due sinusoidi aventi frequenze diverse, e in blu la loro somma:

Ora l'onda finale non ha più una forma semplice, e il suono che essa produce comincia a diventare un po' più interessante.

Se riesco a convincere i miei figli a registrare un paio di note prese da strumenti veri, dovrei riuscire a scrivere un paio di altri post sull'argomento.

Ma perché proprio le frequenze? — sinusoidi

«Chi di voi suona la chitarra?».

«Io, prof!».

«Bene, allora: se prendi una corda che suona una certa nota, cosa succede quando metti un dito al centro e fai suonare solo mezza corda? Che nota si ottiene?».

«Quella di un'ottava sopra».

«Perfetto. E se metti un dito in modo da fare suonare solo un terzo di corda?».

«Boh?».

«Dovresti ottenere la frequenza tripla, no?».

«Forse sì».

«E che nota è?».

«Ah, non so, dipende da qual era la nota iniziale».


Le mie conoscenze musicali si fermano qui, e per sapere il motivo per cui la serie armonica si chiama armonica sono andato dagli amichetti di friendfeed. Uno dei quali aveva già scritto pagine e pagine di teoria musicale e, come se non bastasse, ha anche aggiunto qualche informazione in più sul Post (perché proprio sette note?).

Bene, ora facciamo un passo indietro: perché ci interessano proprio le frequenze dei suoni?

L'onda sonora più semplice, almeno da un certo punto di vista, è l'onda sinusoidale. È semplice perché è facile da descrivere. Prendiamo un punto su una circonferenza e facciamolo ruotare a velocità costante: la sua ombra descrive un moto oscillante che si chiama moto armonico e che, se disegnato su un piano cartesiano mettendo il tempo sull'asse delle ascisse e la posizione dell'ombra su quello delle ordinate, ha come grafico una sinusoide.

Se prendiamo una molla, attacchiamo in fondo un peso, al peso attacchiamo un pennino in grado di scrivere su un cilindro di carta, e facciamo ruotare il cilindro mentre diamo un colpetto al peso in modo da farlo oscillare, possiamo osservare sul cilindro la traccia della sinusoide.

La sinusoide è quindi un'onda semplice da descrivere. Chi ha studiato goniometria sa che esistono tante funzioni goniometriche, ma in realtà ne basterebbe solo una: con quella si possono descrivere tutte le altre.

Una sinusoide è fatta così:

Cosa c'entra tutto questo con i suoni della corda di chitarra? Bé, i suoni sono onde che si propagano attraverso l'aria, e fanno vibrare i nostri timpani. A seconda di come vibrano, noi percepiamo sensazioni differenti. L'onda sinusoidale è il suono più semplice (e anche il più noioso da ascoltare…).

Bastano tre parametri per descriverla: frequenza, ampiezza, fase.

La frequenza ci dice quante oscillazioni vengono fatte in un secondo: l'orecchio umano sano, giovane e in perfette condizioni dovrebbe percepire frequenze nella gamma che va dalle 20 alle 20000 oscillazioni al secondo (che si chiamano Hertz). Ecco un disegno che mostra due onde aventi frequenze diverse (ma stessa ampiezza e stessa fase).

L'ampiezza ci dice quanto alta è un'onda (in pratica, qual è il volume: quando giriamo la manopola dello stereo per ascoltare a volume più alto, stiamo modificando l'ampiezza). Ecco un disegno di due onde aventi ampiezze diverse (ma stessa frequenza e stessa fase).

Infine, la fase ci dice qual è il punto di partenza delle onde. Questo parametro è un po' più difficile da capire, perché in effetti il nostro orecchio non è in grado di percepirlo. Ritornando all'esperimento del peso attaccato a una molla, immaginiamo di averne due: li tiriamo entrambi un pochino verso il basso, e poi li lasciamo andare, ma non contemporaneamente. Prima uno, e dopo un po' l'altro: ecco che le onde che vengono disegnate non sono sovrapposte, ma un po' spostate una rispetto all'altra. Si dice che sono sfasate:

Riassumendo: la frequenza ci dice la nota (se varia, sentiamo una nota più grave o più acuta (le note gravi corrispondono a frequenze più basse, quelle acute a frequenze più alte)), l'ampiezza ci dice il volume (maggiore è l'ampiezza, maggiore è il volume), la fase è, di solito, inascoltabile. In realtà noi abbiamo due orecchie, e se ascoltiamo da una parte una certa onda, dall'altra la stessa onda sfasata, forse ci accorgiamo del fatto che qualcosa non va. Ma bisogna essere allenati.

Ora, nessuno strumento musicale produce un'onda sinusoidale. Forse un buon diapason ne produce una buona approssimazione, e naturalmente gli strumenti elettronici sono in grado di emettere quel tipo di suono; il fatto è che non è molto interessante dal punto di vista musicale, perché è, come dire, noioso. È il tono di libero emesso dalla cornetta del telefono, per esempio.

E allora, a cosa servono le onde sinusoidali in musica? Bé, servono a generare i suoni di tutti gli strumenti.

Questa è un'Applet Java creata con GeoGebra da www.geogebra.org - Java non risulta installato sul computer in uso - fare riferimento a www.java.com zar, 9 Dicembre 2012, Creato con GeoGebra

Nuove frontiere dell'animazione digitale

Questa è una prova: ho costruito una animazione con GeoGebra, l'ho esportata in html e l'ho copiata nell'editor di blogger. L'unico modo per sapere se funziona tutto per bene è pubblicarla.

Quindi, ecco due parole su quello che si dovrebbe vedere: un fotone arriva dal cielo (il pallino rosso). Un telescopio si trova sulla terra e vuole vedere (ehm) il fotone: dato che la terra si muove, il telescopio (che viene trascinato dal movimento della terra) deve essere un po' inclinato. Si tratta del fenomeno dell'aberrazione della luce.

Probabilmente dovrete dire al vostro browser di attivare java su questa pagina.

Aberrazione Questa è un'Applet Java creata con GeoGebra da www.geogebra.org - Java non risulta installato sul computer in uso - fare riferimento a www.java.com zar, 8 Dicembre 2012, Creato con GeoGebra

Enigma

Ci sono tre storie che convergono qui.

La prima è quella che racconta di me bambino, accompagnato da mio papà al cinema a vedere Biancaneve, nella versione in cartoni animati di Walt Disney. Mi racconta il babbo che io passai metà del tempo con gli occhi chiusi, terrorizzato dalla strega cattiva. I miei ricordi non sono molto precisi (avrò avuto sei anni, più o meno), tranne che in un punto: la scena in cui QUELLA MALEDETTA STREGA ORRIPILANTE SCENDE NELLE PRIGIONI DEL CASTELLO, ehm, io l'ho vissuta con gli occhi chiusi da entrambe le mani e al di sotto della linea dei sedili davanti a me, per stare nel sicuro. Ancora oggi, mi sento inquieto al pensiero di quella vecchiaccia col naso bitorzoluto.

La seconda storia è quella che vede ancora me stesso, molto più grande, acquistare e leggere un libro (di cui magari parlerò in un altro momento) su spionaggio e codici cifrati, presentati sia dal punto di vista tecnico che da quello storico. È stato grazie a quella lettura che ho imparato l'importanza che hanno avuto i matematici durante la guerra.

La terza storia è quella raccontata in Enigma, la strana vita di Alan Turing (di Tuono Pettinato e Francesca Riccioni, Rizzoli Lizard, 13.60€ in formato fisico e 11.99€ in formato Kindle)

È una storia a fumetti che racconta di Alan Turing, della sua vita, delle sue scoperte, del suo genio e della sua triste fine. La biografia è molto dettagliata, ma non è un testo matematico (non temete): vengono citate alcune pietre miliari della storia della matematica, come il paradosso di Russell, il programma di Hilbert, il teorema di Gödel, la macchina di Turing e l'omonimo test. Viene poi descritta l'attività di Bletchley Park, e vengono citate le macchine Enigma e Colossus.

Lo scopo di questo libro non è quello di dimostrare teoremi o di parlare di matematica, no. Lo scopo è quello di raccontare una storia, e di invogliare il lettore ad approfondire.

E direi che ci sia riuscito benissimo, se non fosse per quella brutta ossessione di Turing per la storia di Biancaneve. Se, come lui e come il bimbetto della prima storia, siete rimasti ossessionati da Grimilde, non andate a pagina 52 se siete soli in casa.

Anniversari

Sono passati 44 anni dal loro primo (e unico?) bacio:



Auguri.

Cannoni che sparano alle mosche

Teorema: la radice cubica di 2 è irrazionale.

Dimostrazione: se la radice cubica di 2 fosse uguale alla frazione p/q, allora 2 sarebbe uguale a p³/q³, cioè p³ = q³+q³, ma questo contraddice l'ultimo teorema di Fermat.

La dimostrazione vale per tutti gli indici maggiori di 2. Purtroppo l'ultimo teorema di Fermat non è abbastanza potente da dimostrare che anche la radice quadrata di 2 è irrazionale.

---

Dicono gli esperti che, purtroppo, questa è una dimostrazione circolare. La verifica di quest'ultima affermazione è lasciata alla pazienza del lettore.

---

---

Teorema: 56 non è un cubo.

Dimostrazione: dato che 56 = 4³-2³, se fosse un cubo allora l'ultimo teorema di Fermat sarebbe falso.

---

Pare che questa dimostrazione sia stata data da uno studente del Benelux durante una gara di matematica, ma non ne abbiamo le prove.

Come funziona il gps (in teoria)

«La teoria della relatività generale, addirittura?».

«Eh, sì. Partiamo dall'inizio: in orbita intorno alla terra ci sono tanti satelliti che, in sostanza, sono degli orologi molto precisi».

«Oltre a essere dei trasmettitori, immagino».

«Certo, ogni satellite trasmette a terra un codice che lo identifica, l'ora in cui il segnale è stato trasmesso, e le sue effemeridi».

«Effemeridi?».

«Sì, dice a tutti chi è e dove si trova in ogni istante: ciao, sono il satellite Marvin, se non mi colpisce un meteorite mi trovo su questa orbita con questi parametri, che noia».

«Ehm».

«Poi trasmette anche altre informazioni, perché il mondo non è perfetto, la ionosfera fa un po' quello che vuole… ma non complichiamo».

«Forse è meglio; allora, noi a terra col nostro ricevitore gps riceviamo tutte queste informazioni. Poi come facciamo a capire dove ci troviamo? Dobbiamo comunicare col satellite?».

«Impossibile, non abbiamo abbastanza potenza, e non abbiamo l'antenna giusta. Il nostro ricevitore deve cavarsela con quello che riceve».

«E come fa?».

«Prima di tutto, deve conoscere l'ora esatta».

«Vabbé, questo non è difficile».

«Poi ne parliamo, per adesso supponiamo che sia facile. Conoscendo l'ora esatta, il ricevitore può calcolare la distanza dal satellite: il segnale trasmesso viaggia alla velocità della luce, sappiamo quando è stato inviato, sappiamo che ore sono quando lo riceviamo, calcoliamo il tempo impiegato dal segnale per arrivare fino a noi, e da lì ricaviamo la distanza».

«Cosa ce ne facciamo della distanza dal satellite?».

«Ci permette di stabilire una cosa: la nostra posizione si trova sulla superficie di una sfera centrata sul satellite e di raggio uguale alla distanza appena calcolata».

«Una informazione un po' vaga, no?».

«Infatti. Prendiamo allora un secondo satellite, e rifacciamo i calcoli con i suoi dati».

«Otteniamo un'altra sfera?».

«Sì. La nostra posizione allora è in un qualche punto che appartiene sia alla prima che alla seconda sfera. Cioè?».

«Cioè su un qualche punto di una circonferenza! L'intersezione tra le due sfere è una circonferenza, vero?».

«Esatto».

«È ancora un po' vago, però. Ci serve un terzo satellite?».

«Proprio così: col terzo satellite otteniamo una terza sfera, e se la intersechiamo con la circonferenza che già abbiamo…».

«Otteniamo… due punti?».

«Già».

«Ma non va bene».

«Bé, uno dei due punti è quello giusto, e l'altro potrebbe trovarsi sotto terra, oppure in cielo, vai a sapere. Un'idea della nostra posizione dovremmo già averla».

«Non mi piace mica tanto questa imprecisione, però».

«Hai ragione, ma non è un problema, perché c'è un problema più grosso».

«Quale?».

«La precisione del nostro orologio. Per quanto la tecnologia di un aggeggino che costa alcune decine di euro sia avanzata, quanto deve essere preciso?».

«Boh?».

«Prova a calcolare quanto spazio percorre la luce in un microsecondo».

«300 mila chilometri al secondo, per un microsecondo, fa 300 metri… oh, non sono mica pochi».

«Soprattutto se devi capire se, alla rotonda, devi prendere la seconda o la terza uscita».

«Ma quindi i nostri ricevitori gps hanno degli orologi così precisi?».

«Assolutamente no: per questo ci serve il quarto satellite».

«E perché?».

«Perché il quarto satellite produrrà una nuova sfera, e intersecandola con i due punti dovremmo essere in grado di ricavare la nostra posizione, se gli orologi fossero sincronizzati. Dato che non lo sono, la quarta sfera non passerà per nessuno dei due punti».

«E quindi?».

«Quindi sarà il nostro ricevitore, dotato di orologio non in punto, che farà i conti necessari per fare sì che la quarta sfera passi per il punto giusto: dovrà cioè mettere in punto l'orologio, in modo che i conti tornino. Insomma, ci sono quattro incognite da trovare — le tre coordinate spaziali più il tempo — e quattro equazioni fornite dai quattro satelliti».

«Ah, bello».

«Ma tutto questo ancora non basta».

«E perché?».

«Perché c'è la teoria della relatività in ballo».

«Uh».

«I satelliti non sono fermi, ma si muovono. Secondo la teoria della relatività speciale, per un corpo in movimento si verifica il fenomeno della dilatazione dei tempi».

«Ma il corpo deve andare molto veloce, no? I satelliti hanno una velocità così alta?».

«L'hanno abbastanza alta per accumulare un ritardo di 7 microsecondi in un giorno. Robetta, se non fosse per il fatto che la luce ha questa brutta abitudine di andare molto veloce».

«Eh, 300 metri al microsecondo, dopo un giorno il navigatore chissà dove ci porta».

«E non è tutto».

«No? Cosa c'è ancora?».

«La relatività generale: lo spaziotempo nella zona in cui orbitano i satelliti è meno curvo rispetto a quello in cui si trova la superficie della terra; la relatività generale prevede dunque un anticipo degli orologi in orbita, rispetto a quelli che si trovano sulla terra».

«Quindi la relatività ristretta prevede un ritardo e quella generale un anticipo? Allora gli errori si correggono da soli, no?».

«Magari. L'anticipo è di 45 microsecondi, quindi di entità maggiore rispetto al ritardo. Sommando i due errori, abbiamo un anticipo di 38 microsecondi».

«Cominciano a diventare tanti, sono 11 chilometri e 400 metri in un giorno».

«Sono quasi 500 metri in un'ora, quasi 8 al minuto: se anche metti in punto molto precisamente il tuo orologio sulla terra, dopo qualche minuto sei già fuori strada. E quindi le correzioni relativistiche sono necessarie, altrimenti il gps non funzionerebbe».

«Pensa un po', io pensavo che fosse solo roba teorica, questa faccenda della teoria della relatività».

«E invece non è così. A dir la verità, il gps funzionerebbe ugualmente anche senza la comprensione della relatività: gli ingegneri sono abituati a lavorare con errori sistematici, a cercarli e a ridurli al minimo. Anzi, pare che sia successo proprio questo: inizialmente non era stata compresa a pieno la portata degli effetti relativistici, e gli errori furono corretti senza conoscerne la causa. Poi è arrivato qualche teorico che ha spiegato la natura degli errori».

«Bravi, questi ingegneri».

«Non esageriamo, eh?».

«Scusa».

Il problema del fabbricante di tachimetri

«Ma quindi, prof, il tachimetro di un'automobile calcola le derivate?».

«In un mondo ideale, sì: calcola lo spazio percorso in un tempo infinitesimo, fa il rapporto, ed ecco la velocità istantanea. Naturalmente nella realtà no: si basa sui giri che fanno le ruote, o magari sui sottomultipli di un giro, e calcola una velocità media. Comunque, è meglio il gps».

«Per calcolare le velocità?».

«Eh, sì, è più preciso».

«Ma dai, anche i tachimetri sono precisi, non è che siano così tanto scarsi».

«Eppure, basta tenere le gomme più o meno gonfie, oppure averle un po' troppo consumate, e si sbagliano anche loro».

«Massé».

«Proviamo a fare un calcolo».

«Capirai».

«Per calcolare la velocità, o anche lo spazio percorso, ci serve sapere la lunghezza della circonferenza della gomma».

«Uh?».

«Altrimenti come fai a calcolare quanta strada hai fatto, se non sai quanta strada percorri con un giro di ruote?».

«Anche questo è vero».

«Quindi, ci serve il raggio di una ruota. Facciamo circa trenta centimetri?».

«Più o meno, se non prendiamo un SUV».

«Lasciamo perdere i SUV: allora, la lunghezza di una circonferenza di raggio trenta centimetri è circa… 188.5 centimetri. Per fare 100 chilometri, quanti giri fa una ruota?».

«Aspetti che faccio la divisione: viene 53050 giri».

«Bene. Adesso facciamo consumare le gomme, diciamo che dopo molta strada abbiamo perso 5 millimetri di spessore».

«Così tanti?».

«Eh, succede. Poi magari abbiamo anche le gomme un po' sgonfie…».

«Mh, allora il raggio diventa 29.5 centimetri».

«E la circonferenza?».

«Diventa 185.4 centimetri».

«Bene, ora calcola quanta strada fai con 53050 giri di quella lunghezza».

«Mi risulta 98.3 chilometri, possibile?».

«Eh, sì, perdi un paio di chilometri ogni cento».

«E allora anche la velocità non è più quella?».

«Eh, no: se il tachimetro segna 100 km/h, in realtà stai facendo i 98.3».

«Potrei andare più forte!».

«Potresti cambiare le gomme, anche. Comunque, come dicevo, il gps funziona meglio, ed è una tecnologia meravigliosa».

«Perché?».

«Perché senza la teoria della relatività generale non funzionerebbe».

Nel quale l'autore mostra quali perle preziose possano essere celate all'interno di anonimi libretti di matematica

Connessioni

Una delle cose che piacciono di più ai matematici (oltre alle barzellette che fanno ridere solo loro) è riconoscere le connessioni tra argomenti che, apparentemente, non hanno nulla a che fare uno con l'altro.

Per esempio, sul numero di settembre di Rudi Mathematici c'era questo quesito:

quanto vale la somma degli angoli formati dal segmento blu e dal segmento rosso con il segmento nero (insomma, nero-blu + nero-rosso)?

Un primo metodo è quello di usare la goniometria (del resto, stiamo parlando di angoli): si tratta di calcolare arctg(1/3) + arctg(1/2). Se ci ricordiamo la formula della tangente della somma di due angoli, abbiamo che

tg(arctg(1/3) + arctg(1/2)) = (1/3+1/2)(1-1/6) = (5/6)/(5/6) = 1,

e se la tangente è 1 allora l'angolo è di 45 gradi. A me questa soluzione non piace tanto (sarà perché la formula della tangente della somma di due angoli devo sempre ricavarmela, dato che non me la ricordo mai…).

Io avevo inizialmente risolto il quesito in un altro modo, utilizzando la geometria:

Non c'è nemmeno bisogno di spiegare troppo: l'angolo viola fucsia più in basso è l'angolo della diagonale del rettangolo 3×1, l'angolo blu più in alto è quello della diagonale del rettangolo 2×1 (opportunamente ruotato e ingrandito, ma questo non è un problema: l'angolo è sempre quello). E dunque si vede bene (ma si può calcolare facilmente, la griglia è stata disegnata apposta) che la somma dei due angoli è uguale a 45 gradi.

Questa soluzione per me è molto più bella della precedente, almeno qui le cose si vedono. Anzi, il vederle mi ha fatto venire in mente che questo tipo di problemi può essere descritto in un'altro modo: utilizzando i numeri complessi.

Nati per tutto un'altro scopo (la risoluzione delle equazioni di terzo grado), dopo essere stati generalizzati nei quaternioni si è scoperto [in realtà qualcuno l'aveva scoperto anche prima, ma se scrivi in danese nessuno ti considera] che i numeri complessi erano legati anche alle rotazioni nel piano. Un numero complesso può essere espresso in forma cartesiana (spostati in orizzontale di tot e in verticale di tot) oppure in forma polare (ruota di un certo angolo e poi vai avanti di tot). Nella forma polare, la moltiplicazione di due numeri complessi diventa molto semplice: si devono moltiplicare le lunghezze e sommare gli angoli.

Ecco come funziona, allora, la soluzione del problema: prendo il numero complesso (3+i) (spostati a destra di tre e in su di uno — ma tre cosa? — tre unità di misura, aspetta che te la disegno; hai notato che 3 e 1 sono le misure del rettangolo di partenza, quello del testo del problema, vero?)

Adesso moltiplico questo numero per il numero (2+i) (sì, 2 e 1 sono le dimensioni dell'altro rettangolo, ho capito, ma come faccio a moltiplicare  — facile: ti sposti avanti di 2 e in su di 1 — ma due cosa? — sempre due unità di misura, ma attenzione: l'unità di misura attuale è il segmento blu, quindi devi raddoppiare quello)

E ora bisognerebbe andare in su di 1, ma bisogna fare attenzione: rispetto al vettore rosso su non significa andare in verticale. In realtà dobbiamo girare a sinistra di 90 gradi, e quello è il su attuale.

Ed ecco fatto, il risultato del prodotto dei due numeri complessi è il vettore che congiunge il punto di partenza con quello di arrivo

qui disegnato in viola con un tratto più spesso.

Il bello di tutto ciò è che il calcolo può essere fatto in un paio di passaggi:

(3+i)(2+i) = 6+3i+2i-1 = 5+5i,

e, infatti, 5+5i è proprio il vettore risultante, inclinato di 45 gradi (se vogliamo, il segmento avente per estremi il punto di coordinate (5,5) e l'origine forma, con il semiasse positivo delle x, un angolo di 45 gradi).

Naturalmente la moltiplicazione poteva essere svolta anche nell'altro senso, moltiplicando (2+i) per (3+i). Il risultato algebrico è naturalmente lo stesso, l'interpretazione geometrica invece è leggermente diversa. La riassumo in una sola figura:

Il vettore 2+i (in blu) viene moltiplicato per 3 e poi ruotato di 90 gradi, e il risultato è sempre quello di prima.

Morale della storia: la goniometria, la geometria analitica, i numeri complessi, il calcolo vettoriale sono modi diversi di descrivere la stessa cosa. E quando i matematici riescono a intravedere, al di sotto della descrizione particolare, ciò che c'è realmente, vanno in brodo di giuggiole.

Sono una persona orribile

«Buongiorno».

«Buongiorno prof».

«Bé? Dove sono tutti gli altri?».

«Eh, han fatto sciopero…».

«Ma noo, ma come, ma dai, ma uffa, E ADESSO COSA FACCIO?».

«Eh?».

«Vi interrogo tutti».

«Ma no! Non è giusto, e poi noi siamo qui e…».

«Va bene, va bene, ho capito. Allora via, finisco il programma così gli altri SI ARRANGIANO QUANDO TORNANO».

«Ma come, a ottobre, finisce il programma? Dai, prof».

«Uff. E cosa facciamo?».

«Ci spiega finalmente quella faccenda del triangolo col buco?».

«Ah, va bene, via, quelli che rompevano tanto per sapere la storiella sono rimasti a casa, allora ve la spiego COSÌ IMPARANO!».

«Ehm».

«Vabbé, comunque sia la storia è questa: sono andato da un gioielliere e ho preso in prestito una lastra d'oro, ve la disegno: è la figura in basso».

«Quella col buco?».

«Sì, ma il gioielliere mi ha dato la lastra senza buco, poi io sono andato a casa e ho fatto il buco, mi sono messo in tasca il quadratino d'oro, e ho ritagliato la la lastra in quattro parti, come nella figura».

«E poi?».

«E poi le ho ricombinate come nella figura in alto. A quel punto, ho restituito la lastra al gioielliere, guadagnando un quadratino d'oro».

«Mh».

«Il giorno dopo sono tornato dal gioielliere, mi sono rifatto prestare la lastra, e ho rifatto il giochetto. Dopo essermi messo in tasca il quadratino d'oro, ho restituito la lastra».

«Ma come?».

«L'ho fatto per molto tempo, e adesso SONO RICCHISSIMO! Ho la casa piena di quadratini d'oro, ci posso fare il bagno dentro».

«Ma cosa dice, prof?».

«Oh, fai i conti, guarda la figura: con i pezzi della figura in basso riesco a ricostruire la figura intera. Ogni volta che lo faccio, guadagno un po' d'oro. Potrei anche smettere di lavorare, ma vengo a scuola solo per non fare sapere a tutti che sono ricco».

«Ma davvero?».

«Certo, ho trovato il modo di creare la materia dal nulla».

«Forse c'è un trucco?».

[tagliamo la spiegazione del trucco, tanto lo conoscono tutti — se qualcuno non lo conosce, è un buon esercizio scoprire cosa c'è che non va nel ragionamento (perché, no, non sono diventato ricchissimo)]

Suona la campana.

«Bene, ragazzi, vado, per quanto riguarda i compiti per la prossima volta…».

«Ma no, ci dà anche i compiti, noi che siamo stati a scuola dobbiamo farli e quegli altri invece che sono stati a casa…».

«DICEVO, per quanto riguarda i compiti, lascio a voi l'onere di comunicarli ai vostri compagni».

«Ma quali sono?».

«Io non so niente, pensateci voi, sentitevi liberi, fategliene fare un po'».

«Cioè, lei sta dicendo che…».

«Oh, se li vuoi fare anche tu…».

«AH OK VA BENE HO CAPITO».

«Non esagerate, però, altrimenti se ne accorgono».

«Tranquillo, prof, ci pensiamo noi».

Somme di cubi senza parole

1³+2³+…+n³ = (1+2+…+n)².

Considera l'aragosta

Considera l'aragosta, di David Foster Wallace, Einaudi, 14.45€ in formato cartaceo, è un'altra raccolta di saggi, o di esperienze di vita vissuta, che sto leggendo in questi giorni.

Dico che sto leggendo perché ho deciso di commentare ogni saggio subito dopo averlo finito, senza attendere di aver concluso la lettura di tutto il libro (naturalmente questo post sarà pubblicato alla fine).

Cominciamo.


Il figlio grosso e rosso

Ho un amico che è entusiasta di Las Vegas. Davvero, quando racconta degli hotel giganteschi, del vulcano finto, delle battaglie navali, della zona divertimenti per le famiglie, dei casinò e dei divertimenti un po' meno per famiglie, è sinceramente convinto della loro bellezza. Io rido, ma vabbé.

Ecco, in questo articolo si parla della visita a Las Vegas fatta da DFW in occasione degli Avn awards. Non metto link per cercare di mantenere un'aria di rispettabilità in questo blog, semmai googlate (e, se non avete il safesearch attivo, accertatevi almeno di non avere qualcuno alle vostre spalle). Bene, se anche a voi la descrizione delle bellezze di Las Vegas fatta dal mio amico vi è parsa un po' kitsch e vi ha fatto ridere, rimarrete certamente estasiati (o inorriditi, o tutte e due le cose, a seconda della vostra predisposizione d'animo) nel leggere di questo particolare aspetto di Las Vegas.


La fine di qualcosa senz'altro, verrebbe da pensare
(Su Verso la fine del tempo, di John Updike)

Nove pagine di critica abbastanza sferzante su un romanzo che non ho mai letto di un autore che non conosco. Non importa, c'è una bella descrizione del protagonista del romanzo, che si riflette in considerazioni varie sull'autore del romanzo stesso. Da leggere per poter arrivare a godere dell'ultima frase.


Alcune considerazioni sulla comicità di Kafka che forse dovranno essere tagliate ulteriormente

«Potete chiedere di immaginare che tutte le sue storie siano una specie di porta. Di immaginare noi che ci avviciniamo e battiamo a questa porta, sempre più forte, battiamo e battiamo, non solo perché vogliamo entrare, ma perché ne abbiamo bisogno; non sappiamo cosa sia ma possiamo sentirlo, questo desiderio disperato e assoluto di entrare, e battiamo e spingiamo e calciamo. Finché ecco che la porta si apre… e si apre verso l'esterno — eravamo già dove volevamo essere sin dal principio. Das ist komisch».


Autorità e uso della lingua (ovvero, politica e lingua inglese è ridondante)

Un saggio sull'uso della lingua inglese. All'inizio una pagina scritta dalla traduttrice avverte delle difficoltà incontrate durante la traduzione in italiano di un saggio riguardante l'uso dell'inglese. Segue una pagina scritta in corpo 4, immagino (65 righe e due titoli), di testo non tradotto riportante una serie enorme di errori.

Da segnalare per i non inglesi: una interessante considerazione sull'aborto e la figura dello Snobino — che tanto ricorda Tapparella.


La vista da casa della sig.ra Thompson

Come DFW ha vissuto la giornata dell'11 settembre 2001.


Come Tracy Austin mi ha spezzato il cuore

Un commento (un po' caustico) all'autobiografia della tennista Tracy Austin.


Forza, Simba
Sette giorni in Cammino con un Anticandidato

Come funzionava la campagna per la candidatura alle primarie repubblicane del 2000 di John McCain. Un lungo resoconto di come vivono i giornalisti al seguito del candidato, e una descrizione di tutto il baraccone politico americano. Interessante.


Considera l'aragosta

Il festival dell'aragosta del Maine, dove le aragoste diventano cibo comune e a buon mercato.


Il Dostoevskij di Joseph Frank

Questo l'ho sfogliato velocemente, e non l'ho letto con attenzione: dopo le prime pagine l'argomento non mi ha attirato abbastanza. DFW che parla del professor Frank che parla di Dostoevskij.


Commentatore

E anche questo l'ho solamente sfogliato: la struttura del testo, con frecce che puntano a riquadri e altre frecce che dai riquadri puntano a sottoriquadri, all'inizio è carina, ma dopo un po' diventa fastidiosa.

Una misteriosa costante matematica — 2

«Per ottenere un metodo veloce, anche se approssimato, per calcolare la somma dei primi n termini della serie armonica, dobbiamo dare un'occhiata a questo grafico».

«Uh, e cosa si vede?».

«Allora, la funzione rossa è y = 1/x. Se osservi bene, in corrispondenza dei numeri naturali sono disegnati dei segmenti verticali che intersecano la curva».

«Vedo».

«Quindi, il primo punto sulla curva rossa avrà come y il valore 1».

«Certamente, basta sostituire a x il numero 1, e risulta 1/1».

«Bene. Il secondo punto sulla curva rossa invece avrà ordinata uguale a 1/2».

«Giusto, il terzo avrà come y il valore 1/3, il quarto 1/4, e così via».

«Bene. Ora calcola l'area di ognuno di quei rettangoli che sono disegnati, cioè quelli aventi base sull'asse delle x».

«Allora, intanto hanno tutti base uguale a 1».

«Giusto».

«Quindi l'area è data dall'altezza».

«Ancora giusto».

«Quindi il primo rettangolo avrà area 1, il secondo 1/2, il terzo 1/3, e così via».

«Perfetto. Quindi possiamo visualizzare la somma dei primi n termini della serie armonica semplicemente osservando quei rettangoli: la somma che vogliamo calcolare è uguale alla somma delle loro aree».

«Ok, ma non riusciamo a calcolarla?».

«Non direttamente. Però continuiamo l'esame del grafico: siamo in grado di calcolare l'area che sta sotto alla curva rossa».

«Davvero?».

«Sì, si utilizza il calcolo integrale. Risulta che l'area che va dal punto di ascissa 1 al punto di ascissa n+1 (cioè l'area sotto ai primi n rettangoli) è uguale al logaritmo naturale di n+1. In formule, un Vero Matematico scriverebbe questo:».

«Va bene, e ora? L'area sotto la curva rossa non è uguale a quella dei rettangoli».

«No, la differenza è appunto data dalla somma delle aree grigie».

«Ed è una cosa che sappiamo calcolare?».

«Non esattamente, ma possiamo dire una cosa importante: la somma di quelle aree è limitata. In particolare, è minore di 1».

«E come facciamo a dirlo?».

«Se anche quelle aree andassero avanti all'infinito, potremmo comunque pensare di spostarle tutte a sinistra, infilandole nel primo rettangolo (che poi è un quadrato, ma non ha importanza)».

«Vero».

«E ci starebbero tutte, senza sovrapporsi».

«Anche questo è vero».

«E lascerebbero un po' di spazio libero».

«Ah, ho capito! Visto che l'area del rettangolo in cui sono contenute è uguale a 1, la loro somma è minore di quel valore».

«Perfetto: ora che sappiamo che quel valore esiste, ci basta un computer per calcolarlo. I matematici l'hanno fatto, naturalmente, e nel 2010 erano note 29844489545 cifre. Non so se il record sia stato superato ultimamente».

«Mica poche».

«Nonostante questo, ancora non si sa se sia un numero razionale o irrazionale».

«Ah».

«Intanto gli abbiamo dato un nome: si chiama costante di Eulero-Mascheroni, e vale circa 0.5772».

«Ok. E quindi possiamo usarla per il problema delle figurine?».

«Anche, sì. Ma non sarebbe quello lo scopo, insomma».

«Immagino, eh».

«Il fatto è che quella costante è legata alla funzione di Riemann, e quindi al problema dei numeri primi».

«Uno dei problemi del millennio?».

«Esattamente. Probabilmente dimostrare la sua irrazionalità potrebbe portare a fare passi avanti in quel senso, o addirittura a risolvere la congettura di Riemann. Si dice che Hardy abbia offerto la sua cattedra a Oxford a chi fosse riuscito a dimostrare l'irrazionalità della costante di Eulero-Mascheroni. Hilbert stesso considerò questo problema come inaffrontabile, un problema davanti al quale i Veri Matematici non sanno come muoversi, e se ne stanno lì sconsolati».

«Addirittura».

«Conway e Guy sono pronti a scommettere che sia trascendente, ma credono anche di non avere abbastanza tempo per riuscire a vedere la dimostrazione».

«Ma dai».

«Ed è stato dimostrato che se questa benedetta costante fosse davvero razionale, il suo denominatore dovrebbe essere maggiore di 10²⁴²⁰⁸⁰».

«Vabbé, dai, è irrazionale. Solo la mente malata dei Veri Matematici si può ostinare a cercare una dimostrazione che permetterebbe di dire qualcosa sulle cifre dopo la 29844489545esima».

«Eh».

«Alla fine, quante figurine dovremmo comprare per completare quel famoso album da 719 calciatori?».

«Allora, il calcolo esatto sarebbe dato dalla somma dei termini della serie armonica dal primo fino al 719-esimo, il tutto moltiplicato per 719:».

N = 719(1+1/2+1/3+…1/719).

«E per non fare tutto a mano, come si fa?».

«Si usa la relazione approssimata che abbiamo visto prima. Se indichiamo con γ la costante di Eulero-Mascheroni, abbiamo che».

«Vediamo un po', se n = 719 mi viene 5145.5. Argh».

«Si fanno affari con le figurine, eh?».

Una misteriosa costante matematica — 1

Una nota marca di merendine per la prima colazione inserisce, in ogni scatola, una figurina di un matematico famoso. Il produttore sostiene che tutti i matematici sono distribuiti uniformemente, e che la serie completa è composta da 8 figurine (siamo solo alla prima edizione). Quante scatole ci aspettiamo di dover comprare per completare la collezione?

(Spoiler alert: se volete provare a risolverlo da soli, non andate oltre, tornate dopo)

Possiamo risolvere il quesito ragionando in questo modo: acquistando la prima scatola ci assicuriamo la prima figurina, fin qua è facile. Con la seconda scatola possiamo trovarci di fronte a due possibilità: siamo sfortunati e troviamo la figurina che abbiamo già, oppure siamo fortunati e troviamo una figurina che ci manca. Il primo caso si verifica con probabilità 1/8, il secondo invece con probabilità 7/8.

Dato che la probabilità di ottenere una nuova figurina è 7/8, dovremmo acquistare 8/7 di scatola per ottenerla.

«Certo, andiamo in negozio, prendiamo una scatola e poi seghiamo un pezzettino di un'altra scatola».

«Ma no, questo è un discorso di media, è chiaro che per avere la figurina o compri una scatola e sei fortunato, o sei meno fortunato e ne devi comprare due, o ancora meno fortunato e ne devi comprare tre, quattro, o di più».

«E allora cos'è questa faccenda degli 8/7 di scatola?».

«Significa che, se prendiamo tanti collezionisti, e facciamo la media sul numero di scatole che servono per ottenere due figurine, il risultato sarà vicino a 1+8/7 (più collezionisti ci sono, migliore sarà l'approssimazione)».

«Vabbé. E quindi, se vogliamo la terza figurina, dobbiamo ragionare allo stesso modo?».

«Sì, la terza figurina sarà diversa dalle prime due con probabilità 6/8, e quindi dovrai comprare 8/6 di scatola».

«Sempre in media».

«Certo. Poi ce ne vorranno 8/5, 8/4, e così via fino a 8/1».

«Quindi per ottenere l'ultima figurina devo comprare otto scatole?».

«Sì, hai una sola possibilità su otto di trovare quella giusta, quindi ti toccherà acquistarne proprio otto».

«Ho capito. Il risultato finale allora sarà 1+8/7+8/6+…+8/2+8/1. Cioè…».

«761/35».

«Eh, fammi fare il calcolo che capisco meglio… fa 21.7, circa».

«Quindi con 22 scatole hai buone probabilità di cavertela».

«Però, risulta quasi il triplo del numero iniziale. Comincio a capire come funzionano le raccolte di figurine».

«Eh, sì, pensa a quante figurine può contenere un album di calciatori, e fai qualche conto…».

«La regola per il calcolo mi sembra semplice».

«Sì, e se modifichi un po' la formula diventa ancora più chiara. Per esempio, nella formula che abbiamo usato per le otto figurine, prova a raccogliere a fattor comune tutti quegli otto che stanno al numeratore».

«Mi viene 8(1/8+1/7+1/6+…+1/2+1). Mh, mi ricorda qualcosa».

«Se li riordini, ti accorgerai che si tratta dei primi termini della serie armonica: 8(1+1/2+1/3+…+1/7+1/8), di cui si è già parlato in passato, anche in qualche vecchio Carnevale della Matematica [1][2]».

«Uh, vedo».

«Ti faccio vedere anche cosa significa che in media bisogna acquistare 21.7 scatole: ho scritto un programma che simula duemila collezionisti di figurine. Ognuno fa i suoi acquisti fino a che non ha ottenuto le otto figurine, poi alla fine viene fatta la media tra tutti. Eccolo qua:».

from random import randrange

N=8

#nella lista ci vanno i numeri da 0 a 7

def colleziona():

  conta=0
  lista=[]
  while 1:
    x=randrange(N)
    conta+=1
    if x not in lista:
      lista+=[x]
    if len(lista)==8:
      break

  return conta


media=0
for i in xrange(2000):
  media+=colleziona()
  #print float(media)/(i+1)

print "Media:", float(media)/2000

«Mi pare abbastanza chiaro».

«Ho fatto anche un paio di grafici per vedere che, all'aumentare del numero dei collezionisti, il valore medio si stabilizza sempre più verso il famoso 21.7».

«E come mai sono diversi?».

«Perché ogni prova è diversa dalle altre. La cosa importante è vedere che l'andamento si stabilizza, anche se nel secondo grafico si stabilizza più lentamente».

«Probabilmente 2000 prove sono ancora poche».

«Già. Devi pensare che 21.7 scatole sono, appunto, una media, ma ci possono essere collezionisti fortunati che se la cavano con 8 scatole e altri meno fortunati che ne devono acquistare ben più di 22. Anzi, mi basta aggiungere un paio di righe al programma per vedere qual è il record negativo di acquisto scatole:».

media=0
record=0
for i in xrange(2000):
  m=colleziona()
  if record < m:
    record = m
  media+=m
  print float(media)/(i+1)

print "Media:", float(media)/2000,record

«Ah, certo, così tieni in memoria il valore massimo di scatole da acquistare: quanto risulta?».

«Faccio girare il programma: ecco, 72».

«Però, sfortunato quel poveraccio che deve acquistare 72 scatole».

«Eh, già. E pensa a quelli che collezionano figurine di calciatori: nella collezione dell'anno scorso c'erano 690 figurine».

«Quante?!».

«Più altre 29 con un codice strano: in tutto 719».

«Santo cielo! Ma bisogna acquistarne un numero colossale».

«Quante?».

«Eh, mi tocca fare una somma lunghissima, non c'è un metodo migliore?».

«Se ti accontenti di un risultato approssimato (approssimato molto bene, eh), c'è».