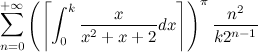Il teorema della non pettinabilità della noce di cocco

Ai matematici piace dare nomi spiritosi alle cose che fanno, ma non sempre ciò che fa ridere un matematico fa ridere il resto del mondo.

C'è un teorema che afferma che non esiste un campo vettoriale continuo non banale (cioè non nullo) tangente ad una sfera. Ma i matematici spiritosi lo enunciano in un altro modo: è impossibile pettinare completamente una noce di cocco (o una palla da tennis, o una palla pelosa generica; qualcuno si spinge a parlare di palle da biliardo coi capelli, per dire). Salta sempre fuori un buchino, o una riga, o una chierica, o un ciuffetto.

Possiamo anche trasportare questo teorema nella realtà: i venti, sulla terra, possono essere rappresentati da vettori tangenti alla superficie (ammettendo che non ci sia spostamento verticale). Allora in ogni istante esiste almeno un punto sulla terra in cui non tira vento. Se consideriamo anche lo spostamento verticale, allora in quel punto l'aria potrebbe muoversi verso l'alto o verso il basso, ma non in orizzontale. Insomma: sulla terra esiste sempre almeno un ciclone o un anticiclone.

Gioco del lunedì — Manufactoria

Siamo in una fabbrica di robot, addetti al controllo qualità. Ogni robot è dotato di una programmazione, che consiste in una sequenza arbitraria di due colori, il verde e il rosso. Noi dobbiamo costruire una catena di montaggio che faccia passare solo i robot che soddisfano a certi requisiti (differenti per ogni livello), e per farlo abbiamo a disposizione delle macchine che possono leggere la sequenza di colori e eventualmente modificarla.

Siamo una specie di macchina di Turing, insomma, anche se un po' più limitata (non possiamo tornare indietro, ma possiamo solo leggere la sequenza di colori in avanti) (gli informatici possono divertirsi a vedere se il sistema è effettivamente equivalente a una macchina di Turing oppure no).

Il gioco è molto coinvolgente, almeno se vi piace programmare. Quindi attenti, prima di cliccare qui…

(via xkcd)

Coi teoremi non si scherza

(Nota preventiva: ciò che segue ha lo scopo di stimolare chi sa a spiegare ciò che segue)

Esiste un teorema che ha un nome un po' particolare: si chiama teorema del libero arbitrio. L'hanno dimostrato, nel 2006, Conway (sempre lui) e Simon Kochen.

Si basa su tre ipotesi, che vado ad elencare; anche queste hanno nomi un po' particolari:

Fin: esiste una velocità massima di propagazione delle informazioni (non necessariamente deve essere la velocità della luce).

Spin: se si misurano le componenti dello spin di una determinata particella di spin uno lungo tre direzioni ortogonali, e si eleva al quadrato, si ottiene sempre la terna 1, 0, 1 o una sua permutazione (questo è un risultato della meccanica quantistica).

Twin: è possibile legare tra loro due particelle elementari in modo tale che una misura di spin al quadrato fatta su una di esse darà sempre lo stesso risultato di una analoga misura, nella stessa direzione, fatta sull'altra particella, anche se le particelle si trovano ad una notevole distanza una dall'altra (e anche questo è uno dei tanti risultati sconcertanti della meccanica quantistica).

Successivamente, l'ipotesi Fin è stata un po' indebolita (irrobustendo così il teorema) ed è stata quindi sostituita dalla

Min: due sperimentatori possono scegliere quali misure effettuare in maniera indipendente uno dall'altro. Quindi non necessariamente tutta l'informazione deve viaggiare a velocità finita: ciò che ci interessa è che l'informazione riguardante le loro scelte su cosa misurare viaggi a velocità finita.

Il teorema dice, più o meno, che se noi siamo liberi di scegliere quale tipo di misura fare, relativamente allo spin di una particella, allora il risultato che otteniamo non dipende dallo stato dell'universo prima dell'esperimento.

In altre parole più ad effetto, se noi possediamo il libero arbitrio, allora anche una certa categoria di particelle elementari lo possiede. Se no, no.

Comunque stiano le cose, la faccenda mi inquieta.

Cose che si imparano e non si dimenticano più

La luna è bugiarda: se è a forma di C, è Decrescente. Se è a forma di D, è Crescente.

Gioco di magia matematica

Pensa a un qualunque numero compreso tra 1 e 1.000.000.000.000.

1. Elevalo al quadrato.

2. Aggiungi il risultato al numero che avevi pensato.

3. Dividi per il numero che avevi pensato.

4. Aggiungi, boh, 23.

5. Sottrai il numero iniziale.

6. Dividi per 6.

7. Indica con k il numero che hai ottenuto.

8. Ora dimostra che i vertici di un qualunque grafo planare possono essere colorati con k colori, al massimo, in modo tale che nessuna coppia di vertici adiacenti abbia lo stesso colore.

9. Calcola

Non ci crederai, ma risulta 3.

(via spikedmath)

Scrutini