“L'inverso del teorema di Pitagora?”.
“Eh, sì”.
“Ma cosa significa inverso?”.
“Ti giro la domanda: cosa dice il teorema di Pitagora?”.
“Dice che il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti”.
“No”.
“Come no?”.
“No: prendi un triangolo equilatero di lato 1 e dimmi se è vero che 1 + 1 = 1”.
“Ma cosa c'entra un triangolo equilatero? Il triangolo deve essere… Ok, non l'ho detto”.
“Già”.
“Riprovo: il teorema di Pitagora dice che in un triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti”.
“Ottimo. Qual era l'errore, quindi?”.
“Avevo dimenticato di specificare il contesto in cui si applica il teorema”.
“Sì, avevi dimenticato l'ipotesi: il teorema di Pitagora vale se il triangolo è rettangolo”.
“E l'inverso, allora?”.
“L'inverso risponde a quest'altra domanda: è vero o no che il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti solo se il triangolo è rettangolo?”.
“Ovvio”.
“Mica tanto ovvio: prendi un triangolo, indica con a, b e c i suoi tre lati, sai che vale la relazione a2 + b2 = c2. Puoi dire che il triangolo è rettangolo?”.
“Ma per forza, no?”.
“NO! NON ESISTONO DIMOSTRAZIONI PER FORZA!”.
“Ok, ok, mamma mia che brutto carattere”.
“Scusa eh, ma se tu sai che il verificarsi di qualcosa implica il verificarsi di qualcos'altro, puoi dire che automaticamente il verificarsi della seconda cosa implica il verificarsi della prima?”.
“Fino a pochi secondi fa avrei detto di sì, ma mi pare di capire che invece non sia così. Ho un po' paura a chiedere perché, però”.
“Prendi un numero divisibile per 4: puoi dire che è divisibile anche per 2?”.
“Certo”.
“Perché?”.
“Perché se contiene 4 contiene anche 2, dato che 4 è divisibile per 2”.
“Questa proprietà vale per tutti i numeri divisibili per 4?”.
“Certo”.
“Puoi dire il contrario? Puoi dire che ogni numero divisibile per 2 è divisibile anche per 4?”.
“Eh, no, non tutti. Se prendo 8 va bene, se prendo 6 no”.
“Quindi questo è un esempio di teorema che funziona in una sola direzione: il suo inverso non è un teorema”.
“Ah”.
“È vero che un quadrato ha quattro angoli retti?”.
“Certo”.
“È vero il contrario? Che se un quadrilatero ha quattro angoli retti allora è un quadrato?”.
“Eh, no, un rettangolo ha quattro angoli retti ma non è un quadrato”.
“Non è detto che lo sia, volendo essere precisi”.
“Può esserlo?”.
“Beh, sì. Se la definizione di rettangolo è quadrilatero con quattro angoli retti, allora esso potrebbe anche essere un quadrato. Ma non è vero che ogni rettangolo è un quadrato”.
“Va bene, ho capito”.
“Tornando al teorema di Pitagora: è vero che se in un triangolo il quadrato di un lato è equivalente alla somma dei quadrati degli altri due lati, allora quel triangolo è rettangolo”.
“A questo punto non so più quale sia la risposta. Direi di sì, ma non so perché”.
“La risposta è sì, anche se ormai il motivo per cui quella risposta è affermativa è sparito dai libri scolastici”.
“Perché?”.
“Non ne ho idea. Pigrizia? Poca voglia di spiegare? Chissà”.
“Ma è una dimostrazione difficile?”.
“No, non direi. Te la mostro, nella versione di Euclide. Cominciamo da un triangolo ABC per il quale vale la relazione AB2 + AC2 = BC2. Eccolo qua”.
“Ok. Quindi non sappiamo se è rettangolo, e vogliamo dimostrarlo”.
“Esatto: vogliamo dimostrare che l'angolo in A è retto”.
“Va bene, cominciamo”.
“Dobbiamo fare una costruzione: costruiamo un segmento DA che forma un angolo retto con CA”.
“Quindi prolunghiamo AB? Ma non sappiamo se l'angolo A è retto oppure no”.
“Esatto, ottimo: non prolunghiamo, ma costruiamo noi un angolo che sia retto. Questo vuol dire che ancora non possiamo sapere se i tre punti D, A e B sono allineati oppure no”.
“Ho capito. Quanto deve essere lungo il segmento DA?”.
“Tanto quanto AB”.
“Perfetto, eccolo qua”.
“Poi congiungiamo D con C e formiamo un triangolo”.
“E, questa volta, sappiamo che è un triangolo rettangolo”.
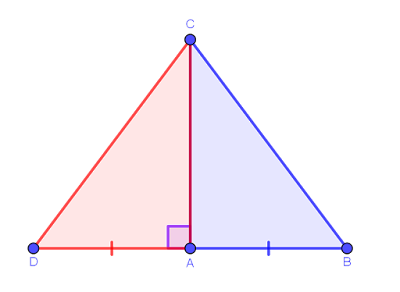
“Proprio così, ecco la figura completa”.
“Ora che si fa?”.
“Scriviamo un po' di uguaglianze. La prima è questa, sei d'accordo? DA2 = AB2”.
“Eh, beh, sì, se DA è uguale a AB lo saranno anche i loro quadrati”.
“Già. Ora aggiungiamo, a destra e a sinistra dell'uguale, la stessa quantità, cioè AC2”.
“Così? DA2 + AC2 = AB2 + AC2”.
“Esatto. Ora guarda cosa c'è a sinistra dell'uguale”.
“C'è la somma dei quadrati di DA e AC… Ah! Il triangolo DAC è rettangolo, quindi per quello posso applicare il teorema di Pitagora, vero?”.
“Certo: questa dimostrazione si appoggia su quel teorema. Prima dimostri il teorema diretto, poi questo”.
“Ah. Ma si può?”.
“Certo, non stai facendo le cose in modo circolare: prima dimostri il teorema di Pitagora, senza usare questo teorema, poi dimostri questo usando quello che hai appena dimostrato”.
“Ok, mi piace. Quindi siamo arrivati al fatto che a sinistra dell'uguale si può applicare il teorema di Pitagora: lo facciamo?”.
“Sì, e quindi possiamo sostituire, al posto di DA2 + AC2, il quadrato dell'ipotenusa, cioè DC2”.
“A destra dell'uguale, però, non posso farlo, perché non so se il triangolo sia rettangolo oppure no”.
“No, ma non ti serve saperlo: per la parte di destra puoi usare direttamente l'ipotesi. Tu sai già quanto vale quella somma”.
“Ehi, ma è vero, è proprio l'ipotesi! So che AB2 + AC2 è uguale a BC2”.
“Certo, e quindi l'uguaglianza è diventata DC2 = BC2”.
“Ma allora posso dire che DC e BC sono uguali”.
“Proprio così: quindi i due triangoli ABC e ACD hanno i tre lati ordinatamente congruenti”.
“E allora sono triangoli congruenti, no?”.
“Sì, è così, per il cosiddetto terzo criterio di congruenza dei triangoli. A questo punto, abbiamo concluso: se i due angoli DAC e CAB sono congruenti…”.
“…dato che DAC è retto, dovrà esserlo anche CAB!”.
“Ed ecco fatto”.
“Avevi ragione, non era difficile. Dicevi che sui libri di scuola non si trova più questa dimostrazione, ma perché? Non è difficile, mi sembra un peccato non metterla”.
“Anche a me”.