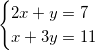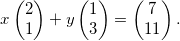“Ma cosa stai dicendo?”.
“Avevi iniziato a parlare dei determinanti, pensavo che prima o poi mi avresti raccontato anche del misterioso metodo di Cramer per la risoluzione dei sistemi”.
“Hai ragione, rimedio subito! Cosa significa risolvere un sistema?”.
“Eh, significa trovare i valori delle incognite che rendono vere entrambe le equazioni, se non mi sbaglio”.
“Giusto, è così. Ma adesso vorrei mostrarti la cosa da un altro punto di vista”.
“Capirai, fai sempre così!”.
“Guarda che è questo il bello della matematica, vedere le cose da diversi punti di vista, riconoscere analogie, creare collegamenti, ed essere felici per questo”.
“…”.
“Comunque, ti propongo un nuovo punto di vista sui sistemi, e lo faccio con un esempio, così abbiamo dei numeri con cui giocare. Eccoti il testo di un esercizio:”.
“Ok, non mi sembra difficile, fammi fare un po' di conti… mi pare che risulti x = 2 e y = 3”.
“Bene, fin qua ci siamo. Adesso permettimi di scrivere il sistema in un modo leggermente diverso, ecco:”.
“Uh? Ma che roba è”.
“Possiamo vederla come una scrittura in forma vettoriale del sistema di prima: quei numeri scritti tra le parentesi sono le componenti dei vettori”.
“Quindi, per capire, all'inizio sto moltiplicando x per il vettore avente componenti 2 e 1?”.
“Esatto. Per dirla in un altro modo, stiamo considerando la prima riga del sistema come una descrizione di quello che succede nel mondo delle ascisse di certi vettori, e la seconda riga, invece, come una descrizione di quello che succede nel mondo delle ordinate”.
“Ma le ascisse sono le x, che compaiono sia nella prima che nella seconda riga. E anche le ordinate, eh”.
“Non fare confusione, le x e le y che vedi nel sistema non c'entrano con le ascisse e le ordinate di cui ti sto parlando. Tu hai un vettore, che ha componenti 2 e 1…”.
“Ascissa 2 e ordinata 1”.
“Esatto. Lo moltiplichi per x, cioè ne vari la lunghezza, e ottieni un altro vettore…”.
“Di ascissa 2x e ordinata x?”.
“Proprio così. Poi hai un secondo vettore, di componenti 1 e 3. Questo lo moltiplichi per y”.
“E ottengo un vettore di componenti y e 3y”.
“Sì. Adesso li sommi: ti ricordi come si fa la somma tra due vettori?”.
“Si fa componente per componente. Il risultato dovrebbe essere il vettore di ascissa 2x + y e di ordinata x + 3y”.
“E queste sono le due righe del sistema. Cioè, le due parti a sinistra dell'uguale”.
“Ah, ho capito. E il sistema quindi ci domanda quanto devono valere x e y perché il vettore risultante sia quello di componenti 7 e 11?”.
“Ottimo, hai detto bene: traducendo in linguaggio geometrico, il sistema ci domanda di quanto devo allungare i due vettori (2,1) e (1,3) perché il risultato sia il vettore (7,11)”.
“E quindi potrei fare anche un disegnino, con questi vettori? Giusto per vedere meglio le cose”.
“Naturalmente. Puoi giocare con la figura qua sotto: in rosso sono indicati i vettori u e v, che sono i vettori (2,1) e (1,3). Puoi trascinare il punto viola dove vuoi, e osservare come devono essere modificati i due vettori dati perché la loro somma dia il vettore che termina sul punto viola”.
“Mh, carino, ma il punto rosso cosa sarebbe?”.
“È il punto di coordinate (7,11), cioè il punto dove tu vorresti fare andare la punta del vettore”.
“Beh, posso trascinarcela sopra, no?”.
“Certo. Se lo fai, puoi vedere come devono essere modificati i vettori u e v in modo tale che la loro somma finisca proprio su (7,11)”.
“Provo… a occhio mi sembra che il vettore u raddoppi…”.
“Eh eh”.
“Cosa c'è da ridere?”.
“Magari ti sembra anche che il vettore v triplichi?”.
“Mh, non riesco a vederlo bene a occhio, ma potrebbe essere. Continuo a non capire perché ridacchi, però”.
“Perché hai già risolto il sistema prima! Non avevi trovato x = 2 e y = 3?”.
“Sì, ma cosa c'entra… Ah! Ma certo! Il fatto che x sia uguale a 2 significa che devo moltiplicare il vettore u per 2, e il fatto che y sia uguale a 3 significa che devo moltiplicare v per 3, e il risultato è proprio (7,11). Ma guarda un po', non avevo mai visto un sistema risolto in questo modo”.
“Bello, vero? In pratica abbiamo interpretato il sistema come un'equazione vettoriale. Se diamo un nome anche al vettore risultante, cioè (7,11)…”.
“A questo punto chiamiamolo w”.
“Bene, se poniamo allora w = (7,11), il sistema che abbiamo scritto prima può essere riscritto così:”.
xu + yv = w.
“Molto semplice”.
“E però non possiamo mica sempre trovare x e y a occhio, no?”.
“Eh, no. Ma questa visualizzazione ci aiuterà molto nella ricerca di un metodo risolutivo”.
“Il famoso metodo di Cramer?”.
“Proprio lui”.
